基于GAMPSO-SVM的大坝变形监控模型

李涧鸣　包腾飞　卢远富　孙鹏明　高瑾瑾

(1. 河海大学 水利水电学院， 南京　210098； 2. 河海大学 水文水资源与水利工程科学国家重点实验室， 南京　210098； 3. 河海大学 水资源高效利用与工程安全国家工程研究中心， 南京　210098)



基于GAMPSO-SVM的大坝变形监控模型

李涧鸣1,2,3包腾飞1,2,3卢远富1,2,3孙鹏明1,2,3高瑾瑾1,2,3

(1. 河海大学 水利水电学院， 南京210098； 2. 河海大学 水文水资源与水利工程科学国家重点实验室， 南京210098； 3. 河海大学 水资源高效利用与工程安全国家工程研究中心， 南京210098)

摘要：建立合理的安全监控模型对实测资料进行实时分析和处理对大坝的安全运行有着重要意义．近年来，支持向量机(SVM)在建立监控模型中得到了广泛应用．但参数的选取对SVM模型的精度有相当大的影响．为了提高参数选择的精度，在标准粒子群算法(PSO)的基础之上，提出了一种加入高斯扰动项的变异粒子群优化算法(GAMPSO)，对支持向量机的参数进行寻优，建立了基于GAMPSO-SVM的大坝变形监控模型，并进行工程实例验证．结果表明，该模型能有效避免陷入局部最优，具有更好的预测精度和泛化能力．

关键词：大坝安全；变形预测；粒子群算法；支持向量机；高斯扰动

大坝变形作为最重要的监测量之一，能够较直观可靠地反映大坝的安全性态．现阶段，大坝安全监控模型主要有多元回归模型[1]和以人工神经网络为代表的人工智能模型等[2-3]．其中，多元回归模型要求观测样本足够充分，且精度受相关性影响．而人工神经网络作为一种仿生算法，理论体系不完备，网络拓扑结构和参数初值选择有一定主观性，并且由于以经验风险最小化为基础，易产生“过拟合”问题，泛化能力较差．支持向量机(SVM)是Vapnik提出的一种机器学习方法[4]，有坚实的理论基础，能较好解决高维数和非线性问题，克服人工神经网络“过拟合”的问题，小样本有很好的泛化能力．但SVM模型中核函数参数σ和惩罚因子C的选择对预测精度影响较大．可以采用粒子群优化算法(PSO)[5]对SVM参数进行寻优．该算法虽具有算法简单，效率高等优点，但存在易陷入局部最优等问题，往往达不到较好精度．本文提出了一种基于高斯扰动的自适应变异粒子群优化算法(GAMPSO)，对SVM模型的参数进行寻优．通过工程实例进行验证，结果表明，GAMPSO-SVM模型具有更高的精度和泛化能力．

1支持向量机

对于回归问题，支持向量机(SVM)的基本思想是利用核函数，将输入的变量映射到一个高维空间中，从而将低维的非线性问题转化为高维空间中的线性回归问题来解决[7]．其实质是一个凸二次规划的求解问题．

对于训练集(xi，yi)，i=1，2，…，n，xi∈Rm，yi∈R．可用非线性映射φ(·)建立向高维空间的映射，并构造回归函数

式中，w为权向量；b为常数．

以结构风险最小化[6]为原则，为使回归函数最优，需满足w的范数‖w‖最小，可转化为

训练样本满足

引入松弛变量，则问题等价于：

式中，ξ为松弛变量，ξ≥0；C为惩罚因子，C>0，需人为拟定．ξ和C的引入放松了条件的限制并对不严格满足条件的点给与相应的惩罚，以控制经验风险和模型复杂度之间的折中并降低对噪声的敏感程度．

引入Lagrange乘子，建立Lagrange函数：

式中，αi为Lagrange乘子．

根据最优化理论转化为求对偶问题，由KKT(Karush-Kulm-Tucker)条件：

可求得：

消去w和ξi，并引入核函数K(xi，yj)，满足Mercer条件，可得线性方程组：

式中，e=[1，1，…，1]T；I为单位矩阵；α=[α1，α2，…，αl]T；Qij=K(xi，xj)．

其中，核函数常用径向基(RBF)核函数，形式为：

可得回归模型：

核参数σ和惩罚因子C的选取对SVM模型的精度有相当大的影响．本文利用GAMPSO算法对参数C和σ进行寻优．

2GAMPSO算法

2.1标准PSO算法

粒子群算法(PSO)的基本思想是把优化问题的解看作搜索空间中的粒子，并由目标函数为粒子确定适应度值．各粒子在解空间中的运动过程中相互合作并传递信息，使位置不停更新，进而使得整个种群逐步逼近最优的目标．

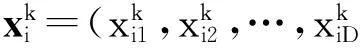
式中，ω为惯性权重，ω>0，用以控制粒子以前速度对当前速度的影响，对于基本粒子群算法，ω取为1；c1，c2为加速常数，分别调整向pbest和gbest方向运动的最大步长；r1，r2为[0，1]区间服从均匀分布的随机数．为防止粒子盲目搜索，将其速度和位置限制在一定区间[-Vmax，Vmax]，[-Xmax，Xmax]．

2.2GAMPSO算法

标准PSO算法应用广泛，但存在后期收敛缓慢，精度低和易陷入局部最优等缺点．因此在其基础上作了一些改进，提出了一种加入高斯扰动项的变异粒子群优化算法(Adaptive Mutation Particle Swarm Optimization based on Gaussian Disturbance， GAMPSO)．在标准PSO算法的基础上进行了如下改进：

1)惯性权重ω的改进

ω对算法的收敛具有重要作用，取值较大有利于全局搜索，收敛速度较快，但搜索较为粗略，而取值较小则有利于局部搜索，易得到更精确的解，但搜索速度慢[8]．基本PSO算法中ω取为1，搜索具有盲目性．Shi等提出了线性递减惯性权重策略[9]，由于初始ω取值较大，后来逐渐减小，可以提高搜索能力．但由于线性变化，全局和局部搜索比例不变，速度控制不合理，搜索时间不够．因此，本文采用余弦递减惯性权重策略，以增加初期迭代的全局搜索时间和后期迭代的局部搜索时间，从而更大程度加快初期搜索的速度，提高后期搜索精度．惯性权重变化如下：

式中，wini，ωend分别表示初始迭代和迭代完成时的惯性权重；K为迭代的次数．

2)引入高斯扰动

标准PSO算法中，随着算法的迭代搜索，粒子表现出较强的群集性，种群多样性显著降低，后期搜索常陷入停滞状态，从而易陷入局部最优解．加入了高斯扰动项可以在搜索过程中在各维度对粒子速度进行扰动，可使算法避开局部最优解的能力进一步加强，保持粒子多样性和活跃性，避免早熟收敛．引入高斯扰动后速度更新公式变为：

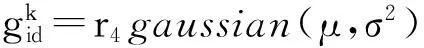
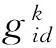
3)引入变异操作

为进一步增强种群多样性借鉴遗传算法的思想，在PSO算法中引入自适应变异操作，尽可能使陷入停滞的粒子跳出局部最优，进入解空间其他区域，从而提高算法找到精度更高解的可能性．具体来说，在每次位置更新后，对粒子随机产生一个[0，1]区间服从均匀分布的随机数r，指定一个阈值μ，对r>μ的粒子进行变异，即随机对其中某一维位置分量进行初始化．

综合以上改进策略，相比标准PSO算法，GAMPSO算法有更高的收敛速度和搜索精度，且可降低迭代过程种群多样性损失，增加粒子活力，有效避免陷入局部最优解．

3大坝变形监测GAMPSO-SVM预警模型的建立

以交叉验证(CV)[10]意义下的准确率作为GAMPSO中的适应度函数，用GAMPSO对SVM中的参数C和σ进行寻优[11]，用训练集建立SVM模型，从而对预测集进行预测分析[12]，大坝变形监测GAMPSO-SVM预警模型的流程图如图1所示．

图1　GAMPSO-SVM模型流程图

4实例分析

某水电站位于安徽省泾县青弋江上游河段，大坝为混凝土重力拱坝，坝高76.3 m．外部变形监测设有高程控制网、平面控制网、视准线、垂线、沉陷和裂缝的观测．本文选择布置在拱冠18号坝段的垂线径向变形监测数据，对所建模型的拟合效果和预测精度进行测试．选取2012年3月3日～2013年7月15日共500组数据用于拟合，2013年7月16日～2013年7月22日共7组数据用于预测．

大坝变形考虑水压，温度，时效的影响[13-15]．水压因子取H，H2，H3，H44项；温度因子分别取上下游T1，T2，T7，T16，T30，T60，T90共14项，时效因子取lnθ1项．共计19个输入变量，其中，H为上游水深；Ti为坝上(坝下)气温计前i天测值的平均值；θ为监测日到始测日的累计天数除以100．

将样本数据归一化到[0，1]区间，归一化后的变量为

其中，Ymax，Ymin分别代表每一组数据的最大、最小值．

初始化参数如下：种群迭代次数为100；种群数量为30；c1，c2均取为2；惩罚因子C和核参数g=1/(2σ2)变化范围分别为[0.1，100]和[0.001，1 000]；惯性权重变化范围为[0.4，0.9]，Vmax=αXmax，α取为0.6；交叉验证参数为5；高斯扰动中μ=0，σ2=|pid|；自适应变异中阈值μ取为0.5．通过GAMPSO寻优得，C=52.065，σ=3.131．

采用复相关系数R和均方差FMSE比较GAMPSO-SVM模型，PSO-SVM模型和逐步回归模型的拟合精度见表1．为直观分析，将GAMPSO-SVM和逐步回归模型的拟合值进行比较如图2所示．结果表明，GAMPSO-SVM模型的拟合精度显著高于逐步回归模型，复相关系数达到0.999．

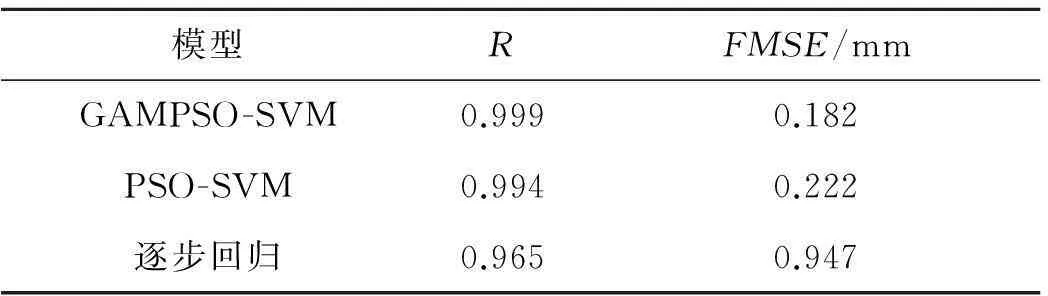
表1　模型拟合时参数比较

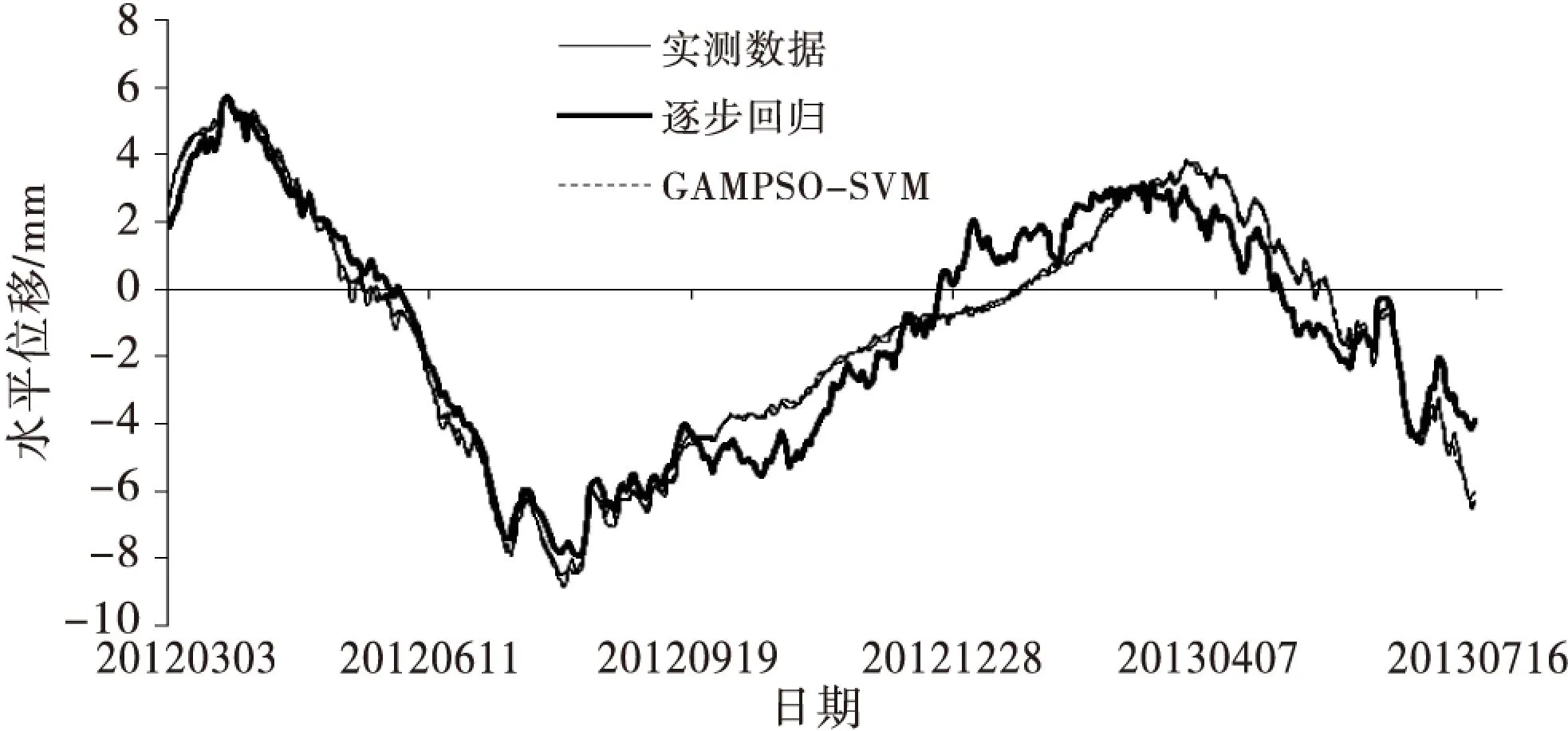
图2　模型拟合曲线图

采用均方差FMSE，平均绝对误差MAE，平均绝对百分比误差MAPE对不同模型的预测精度进行比较，见表2，各模型的预测结果见图3，表3则列出了各模型的预测值和绝对误差．

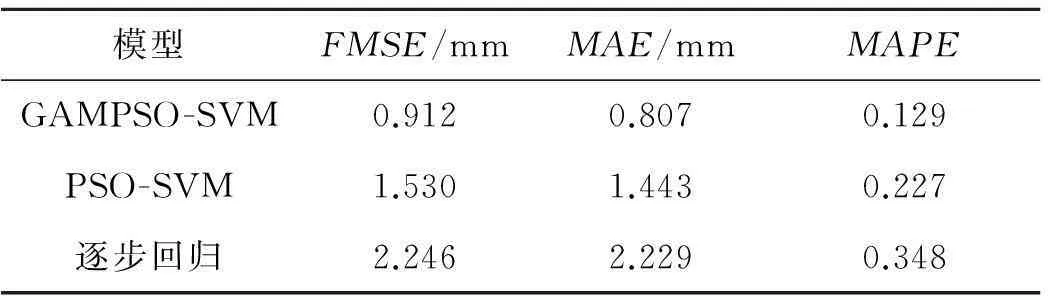
表2　模型预测精度评价指标比较

图3　模型预测曲线图

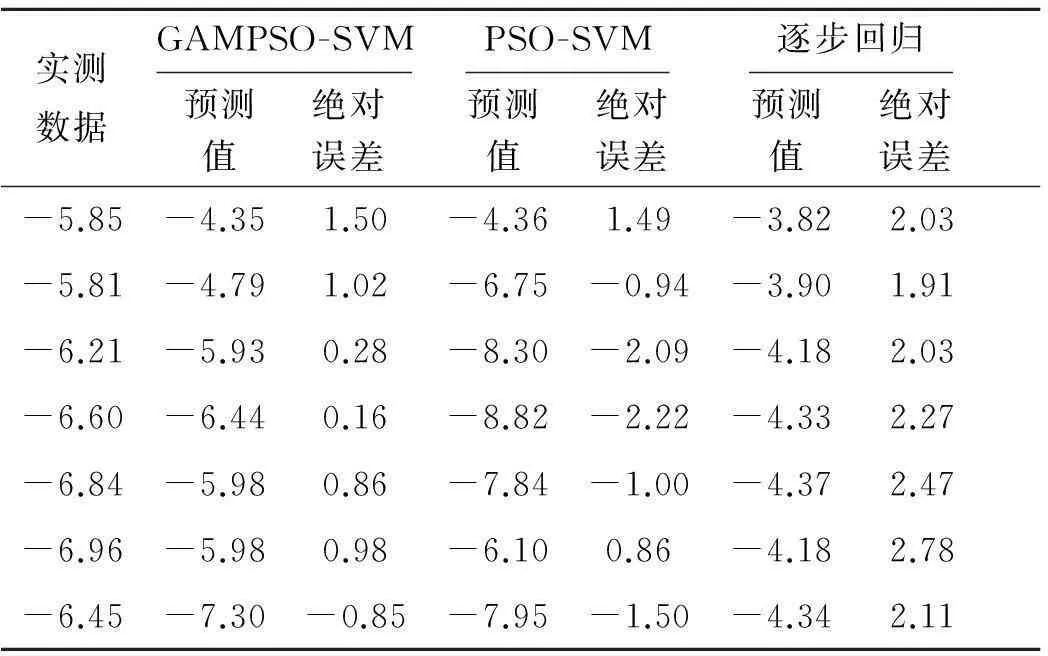
实测数据GAMPSO-SVM预测值 绝对误差PSO-SVM预测值 绝对误差逐步回归预测值 绝对误差-5.85-4.351.50-4.361.49-3.822.03-5.81-4.791.02-6.75-0.94-3.901.91-6.21-5.930.28-8.30-2.09-4.182.03-6.60-6.440.16-8.82-2.22-4.332.27-6.84-5.980.86-7.84-1.00-4.372.47-6.96-5.980.98-6.100.86-4.182.78-6.45-7.30-0.85-7.95-1.50-4.342.11

从以上图表可以看出，逐步回归模型的预测精度较差．而GAMPSO-SVM模型的FMSE、MAE、MAPE均明显小于PSO-SVM模型的，最大误差不超过1.5 mm，表明其预测精度在PSO-SVM模型的基础上有了较大程度提高，该模型有较好的泛化能力．

5结论

本文提出了一种基于高斯扰动的自适应变异粒子群优化算法(GAMPSO)，建立了GAMPSO-SVM模型，并在大坝变形监测方面进行了实例验证，取得了较满意的结果．可得出如下结论：1)GAMPSO算法能较好地克服粒子群算法后期收敛慢和易陷入局部最优等不足，能更加准确地寻找到SVM的参数，故GAMPSO-SVM模型较PSO-SVM模型有较大改进．2)用GAMPSO-SVM监测模型对某大坝变形进行预测．拟合复相关系数达到0.999，预测均方差、平均绝对误差、平均绝对百分比误差分别为0.912、0.807和0.129，均明显小于逐步回归和PSO-SVM模型，最大预测误差控制在1.5 mm以内．故可以证明，与常规模型相比，GAMPSO-SVM变形监测模型具有较好的拟合和预测精度，显著提高了模型的泛化能力，故可应用于解决工程实际问题．

参考文献：

[1]陈久宇，林见．观测数据的处理方法[M]．上海：上海交通大学出版社，1987．

[2]SU Huaizhi， HU Jiang， WU Zhongru． A Study of Safety and Early-warning Method for Dam Global Behavior[J]． Structural Health Monitoring， 2012， 11(3)： 269-279．

[3]王凌．智能优化算法及其应用[M]．北京：清华大学出版社，2001．

[4]Vapnik V N． The Nature of Statitical Learning Theory[M]．New York： Springer-Verlag， 1995．

[5]Kennedy J， Eberhart R． Particle Swarm Optimization[C]． IEEE Int. Conf. on Neural Networks， Piscataway： IEEE Service Center， 1995：1942-1948．

[6]邓乃扬，田英杰.数据挖掘中的新方法-支持向量机[J]．北京：科学出版社，2004．

[7]苏怀智，温志萍，吴中如.基于SVM理论的大坝安全预警模型研究[J]．应用基础与工程科学学报，2009，17(1)：40-48．

[8]陈国初，俞金寿.增强型微粒群优化算法及其在软测量中的应用[J]．控制与决策，2005，20(4)：377-381．

[9]Shi Y， Eberhart R． A Modified Particle Swarm Optimizer[C]． IEEE Int. Conf. on Evolutionary Computation， Piscataway： NJ， IEEE Service Center， 1998. 69-73．

[10] Oh Hee-Seok， Kim Donghoh， Lee Yangjo， et al. Cross-validated Wavelet Shrinkage[J]． Computational Statistics， 2009， 7(6)：573-577．

[11] Chang C C， Lin C J. LIBSVM： A Library for Support Vector Machines[DB/OL]. 2011-10-07．

[12] 刘天祥，包腾飞，等.基于遗传算法的LIBSVM模型大坝扬压力预测研究[J]．三峡大学学报：自然科学版，2013，35(6)：24-28．

[13] 吴中如，沈长松，阮焕祥.水工建筑物安全监控理论及应用[M]．南京：河海大学出版社，1990．

[14] 顾冲时，吴中如.大坝与坝基安全监控理论和方法及其应用[M]．南京：河海大学出版社，2006．

[15] 李珍照.大坝安全监测[M]．北京：中国电力出版社，1997．

[责任编辑王康平]

Study of Dam Deformation Monitoring Model Based on GAMPSO-SVM

Li Jianming1,2,3Bao Tengfei1,2,3Lu Yuanfu1,2,3Sun Pengming1,2,3Gao Jinjin1,2,3

(1. College of Water Conservancy & Hydropower Engineering, Hohai Univ., Nanjing 210098, China; 2.State Key Laboratory of Hydrology-Water Resources & Hydraulic Engineering, Hohai Univ., Nanjing 210098, China; 3.National Engineering Research Center of Water Resources Efficient Utilization & Engineering Safety, Hohai Univ., Nanjing 210098, China)

AbstractIt is important to build a reasonable safety monitoring model to analyze and process the real-time data for the operation of a dam. Recently, the support vector machine(SVM) has been widely used in establishing monitoring models. However, the selection of parameters has a great effect on the precision of SVM. In order to improve the precision of the parameters, on the basis of particle swarm optimization(PSO), a new adaptive mutation particle swarm optimization based on Gaussian disturbance(GAMPSO) method is proposed to optimize the parameters; and the combination of GAMPSO and SVM is used to establish a dam deformation monitoring model. Finally, practical engineering analysis is made. The results show that this model can avoid trapping in local optimum and shows better accuracy and generalization ability.

Keywordsdam safety;deformation prediction;particle swarm optimization;support vector machine;Gaussian disturbance

中图分类号：TV698.1

文献标识码：A

文章编号：1672-948X(2015)06-0042-05

DOI：10.13393/j.cnki.issn.1672-948X.2015.06.009

通信作者：包腾飞(1974-)，男，教授，博士生导师，研究方向为水工建筑物安全监控、评估及反馈分析．E-mail：baotf@hhu.edu.cn