逐步RVM-Markov模型在大坝变形预测中的应用

唐　琪　包腾飞　杜传阳　滕雯雯

(1. 河海大学 水文水资源与水利工程科学国家重点实验室，南京　210098； 2. 河海大学 水资源高效利用与工程安全国家工程研究中心，南京　210098； 3. 河海大学 水利水电学院， 南京　210098； 4. 威海市水利局，山东威海　264200)



逐步RVM-Markov模型在大坝变形预测中的应用

唐琪1，2，3包腾飞1，2，3杜传阳1，2，3滕雯雯4

(1. 河海大学 水文水资源与水利工程科学国家重点实验室，南京210098； 2. 河海大学 水资源高效利用与工程安全国家工程研究中心，南京210098； 3. 河海大学 水利水电学院， 南京210098； 4. 威海市水利局，山东威海264200)

摘要：相关向量机(RVM)模型具有结构稀疏化、核函数选择范围广等特点，应用到大坝变形预测中比支持向量机(SVM)模型更具优势．同时考虑到残差对预测精度的影响，引入Markov链用于预测数据修正，从而得到一种高精度的逐步RVM-Markov组合模型．在实际应用中，RVM模型的泛化能力与SVM相当，向量数量却远小于SVM模型，计算过程得到简化，Mrakov链对残差进行修正后又提高了预测精度．将上述组合模型用于大坝变形实例分析，获得了较好的回归预测效果．

关键词：大坝变形监测模型；相关向量机；Markov链

大坝变形位移是大坝安全监控的重要方面，根据大坝变形实测资料进行分析预测，对了解大坝运行状况，监控大坝和坝基安全起到重要作用[1]．变形测值受水压、温度和时效等因素的影响，会存在一定的趋势变形及周期波动．近些年来，支持向量机(Support Vector Machine，SVM)模型以其在小样本非线性数据回归预测上良好的适用性而在大坝变形监测领域得到广泛研究，但该模型仍存在惩罚系数易选择不当、支持向量个数随样本的增大成线性增长等问题．而Micheal E.Tipping[2]在2001年提出的相关向量机(Relevance Vector Machine，RVM)模型不仅具有与SVM相当的适用范围与泛化能力，而且以其结构稀疏化、核函数不需满足Mercer条件等优点很好地弥补了SVM模型的不足．另外考虑到变形测值波动较大会引起残差规律的变化，降低预测精度，本文利用Markov链模型具有适应大波动数据的优点，将RVM与Markov链模型相结合，并采用逐步更新样本数据的方法，得出一种高精度的变形预测模型，并应用到工程实例中进行验证．

1相关向量机

1.1相关向量机基本原理

相关向量机(Relevance Vector Machine，RVM)与SVM类似，但RVM是在贝叶斯理论框架下进行学习，在先验参数的结构下基于主动相关决策理论(Automatic Relevance Determination，ARD)来移除不相关的点[3]，从而获得稀疏化的模型．

其中，ω=(ω0，ω1，…，ωN)T为权值向量；K(x，xj)为核函数，εi为附加噪声．

相关向量机假定ti服从均值为y(xi)的高斯分布，即p(ti|x)～N(ti|y(xi)，σ2)．

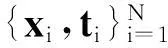
其中t=(t1，…，tn)T，ω=(ω1，…，ωn)T，Φ∈RN×(N+1)，Φ=[φ(x1)，φ(x2)，…，φ(xN)]T，φ(xi)=[1，K(xi，x1)，…，K(xi，xN)]T．

RVM对样本集的训练目的是得到权值向量的后验分布．先定义ω满足ARD高斯先验分布

其中α=(α0，α1，…，αN)T为超参数，每一个αi都相互独立且只与其对应的权值ωi相关[4]．

利用公式(2)(3)，根据贝叶斯公式可得权重ω的后验分布为

从而

其中，Σ为后验协方差矩阵，μ为后验均值向量，B=σ-2I．

对权值进行积分，即

由此可得，p(t|α，σ2)～N(0，C)，其中协方差

通过最大化边缘似然p(t|α，σ2)来进行稀疏贝叶斯学习，为了计算方便，可以转化成对数形式：

对公式(10)关于α求导可以得到迭代公式

其中μi是μ的第i个元素，∑ii是矩阵∑的第i个对角元素，γj=1-αj∑jj．

根据公式(6)、(7)、(11)、(12)可以迭代计算出边缘分布最大化的α和σ，并且出现很多αi趋向于∞的情况，代入公式(11)可得μi趋向于0，则可以将其对应的基向量删除，令对应的ωi=0，从而得到稀疏化的RVM模型．

1.2RVM相较于SVM的优点分析

1)RVM的核函数不需满足梅西(Mercer)定理(关于梅西定理，本文不作详细讨论)，其选择范围要比SVM更广．这一选择条件的放宽，进一步提高了RVM的适用性．

2)针对现实情况常常出现样本重叠的问题，SVM利用惩罚系数来进行处理．但SVM不能对此系数做自动评估，需要手动设置，惩罚系数设置不当，将会引起过拟合的问题而导致结果不理想．由于RVM的参数可以自动赋值，则避免了这一问题．

3)对于同样的样本数据，RVM训练过程中“相关向量”的比重要远远小于SVM“支持向量”的比重．SVM中“支持向量”的个数随着其训练样本的增大而线性增加，遇到较大的训练样本时，会影响其最终的测试速度，而RVM的“相关向量”个数增长速度相对于“支持向量”则要慢了很多．这一特性，使得RVM在某些对实时性要求较高的情况之下，能表现得更为理想．

2Markov链修正模型

2.1马尔科夫过程基本原理

马尔科夫过程(Markov Process)是一个无后效性的随机过程，具体是指当ti时刻所处状态为已知时，大于ti时刻所处状态的概率特性只与过程在ti时刻所处状态有关，而与过程在ti时刻以前的状态无关[5]．而马尔科夫链(Markov Chain)就是指具有马尔科夫性质的状态和时间均离散的随机过程．在大坝安全监测中，各个测点的垂直位移、水平位移、应力、渗流等物理量数据均是与时间相关的状态函数，并且状态和时间均离散，是典型的马尔科夫随机过程．

设V(0)为初始状态E1的初始向量，则经过k步转移后，向量V(k)可通过下式求得：

2.2马尔科夫链修正残差

利用马尔科夫链对RVM模型预测结果进行修正，首先求出拟合值与实测值的残差序列，根据残差序列划分概率区间，通过各个状态向下一个时段的转移的频率可以计算出转移概率，进而构造出转移概率矩阵[6]，本文采用1步转移矩阵，即k=1．

在用RVM模型进行预测时，根据式(16)进行残差修正：

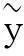
3逐步RVM-Markov大坝变形预测模型实现步骤

混凝土坝的变形位移主要考虑水压、温度和时效的影响[7]，因此可以采用如下统计模型：

其中，δH、δT、δθ分别为水压分量、温度分量和时效分量，H、H0表示监测日和始测日的上游水头，t为监测日到始测日的累计天数，t0为系列监测资料中的第一天到始测日的累计天数，θ=t/100，θ0=t0/100．该统计模型共包括与水压、温度、时效相关的10个输入向量，输出向量为大坝变形位移．

另外，还需按下式对监测数据进行标准化处理，使处理后的数据保持在[0.1，0.9]，以提高学习速度：

其中xmax和xmin是每组监测数据的最大值和最小值．

本文将马尔科夫链与RVM模型相结合，并进一步改进，采用逐步更新的方法，以期提高长期预测的精度．首先根据N期实测数据建立模型并进行预测，得到第N+1期预测值，然后去除第一期数据并加入第N+1期预测数据，再得到第N+2期预测值，依次类推，即总是取最近的N期数据重新建立模型对下一期数据进行预测．

综上，逐步RVM-Markov预测模型的算法流程图如图1所示．

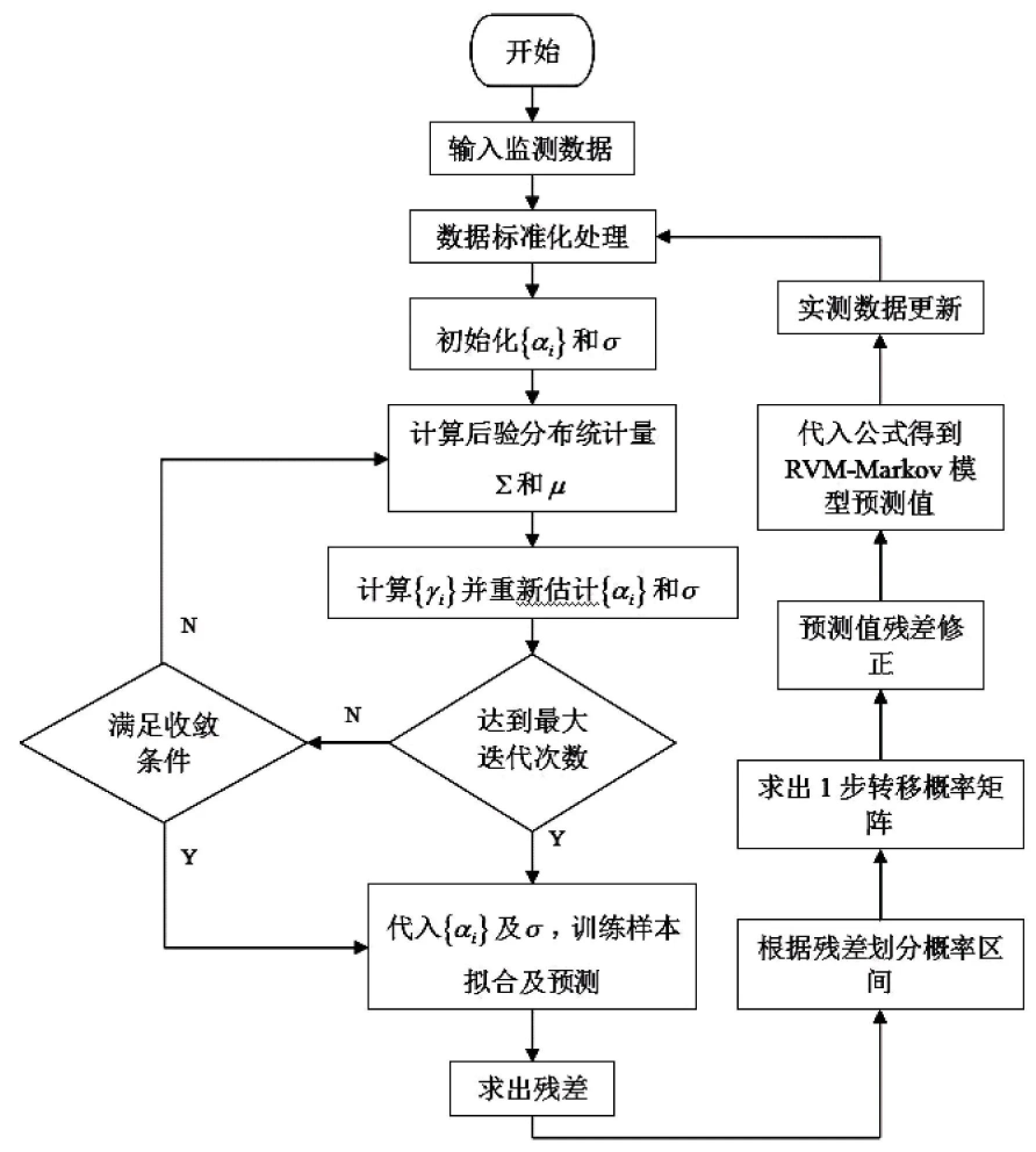
图1　逐步RVM-Markov模型回归预测流程图

4工程实例

某水电站位于我国安徽省泾县，水库总库容24.76亿m3，年发电量3.16亿kW·h．其坝型为重力拱坝，最大坝高76.3m，坝顶高程126.3m．取该坝8号坝段坝体垂线2009年2月1日至2013年2月13日期间的监测资料进行分析，由于相邻两天数据相近不具有代表性，因此每7d取一组数据，共得到210组径向位移监测数据为样本，前200组用于拟合，后10组用于预测．

首先将2009年2月1日至2012年12月5日这200组数据进行标准化处理，然后代入RVM模型训练，核函数选择高斯径向基(RadialBasisFunction，RBF)核函数，核参数 取0.7，得到一系列拟合值．将位移实测值与拟合值相减得到残差，其中上限为1.04mm，下限为-0.86mm，据此将残差序列分为4个区间，见表1．

表1　概率区间划分

在预测过程中，如果模型的残差超出区间边界值，则大于1.04 mm时归于状态IV，小于-0.86 mm时归于状态I．将残差代入马尔科夫链分析，求得1步转移概率矩阵如下：

将以上各计算结果代入公式(16)进行残差修正即可得到RVM-Markov模型拟合值，其拟合效果见图2．然后用逐步更新学习样本的方法预测2012年12月12日至2013年2月13日的10组数据，逐步RVM-Markov模型的预测结果见表2．

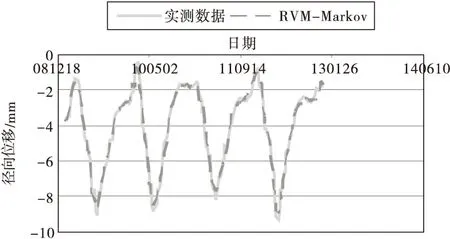
图2　RVM-Markov模型拟合曲线图

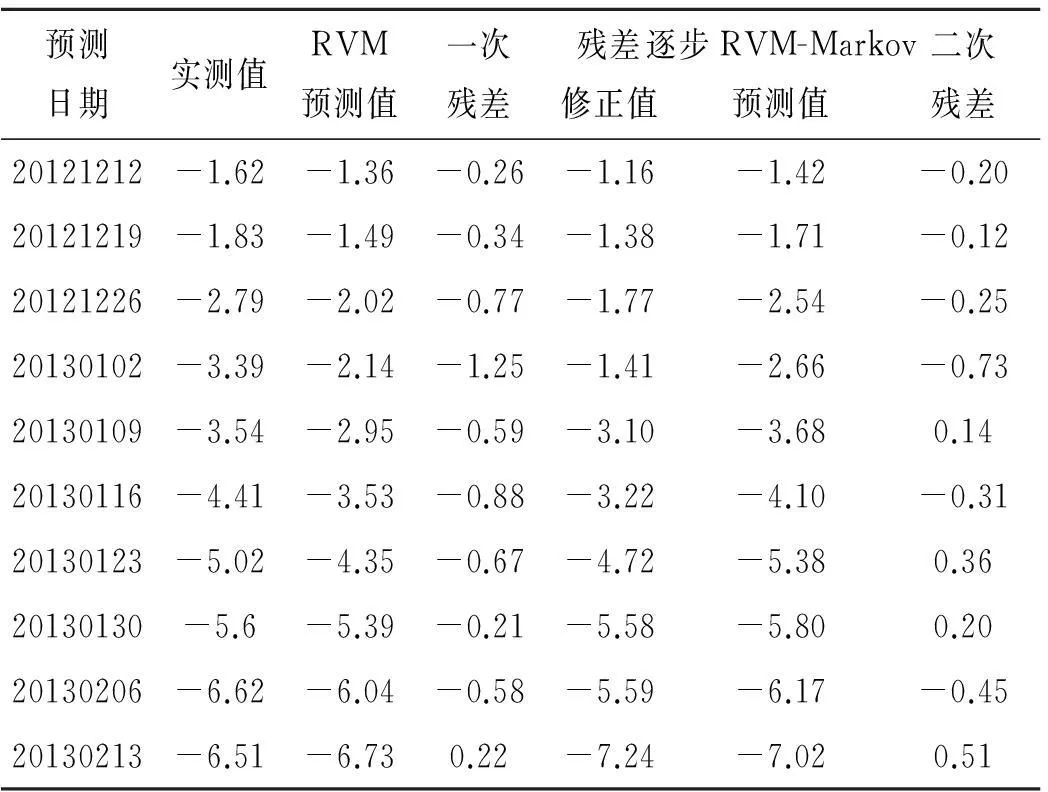
预测日期实测值RVM预测值一次残差残差修正值逐步RVM-Markov预测值二次残差20121212-1.62-1.36-0.26-1.16-1.42-0.2020121219-1.83-1.49-0.34-1.38-1.71-0.1220121226-2.79-2.02-0.77-1.77-2.54-0.2520130102-3.39-2.14-1.25-1.41-2.66-0.7320130109-3.54-2.95-0.59-3.10-3.680.1420130116-4.41-3.53-0.88-3.22-4.10-0.3120130123-5.02-4.35-0.67-4.72-5.380.3620130130-5.6-5.39-0.21-5.58-5.800.2020130206-6.62-6.04-0.58-5.59-6.17-0.4520130213-6.51-6.730.22-7.24-7.020.51

为了便于直观地表现出逐步RVM-Markov模型的优越性，又采用SVM、RVM模型进行回归预测，将3种模型的预测效果进行对比见图3．利用各自的均方差来反映不同模型的回归预测精度，同时记录支持向量与回归向量的个数来比较SVM与RVM模型的复杂程度，对比效果见表3．

图3　3种模型预测曲线图

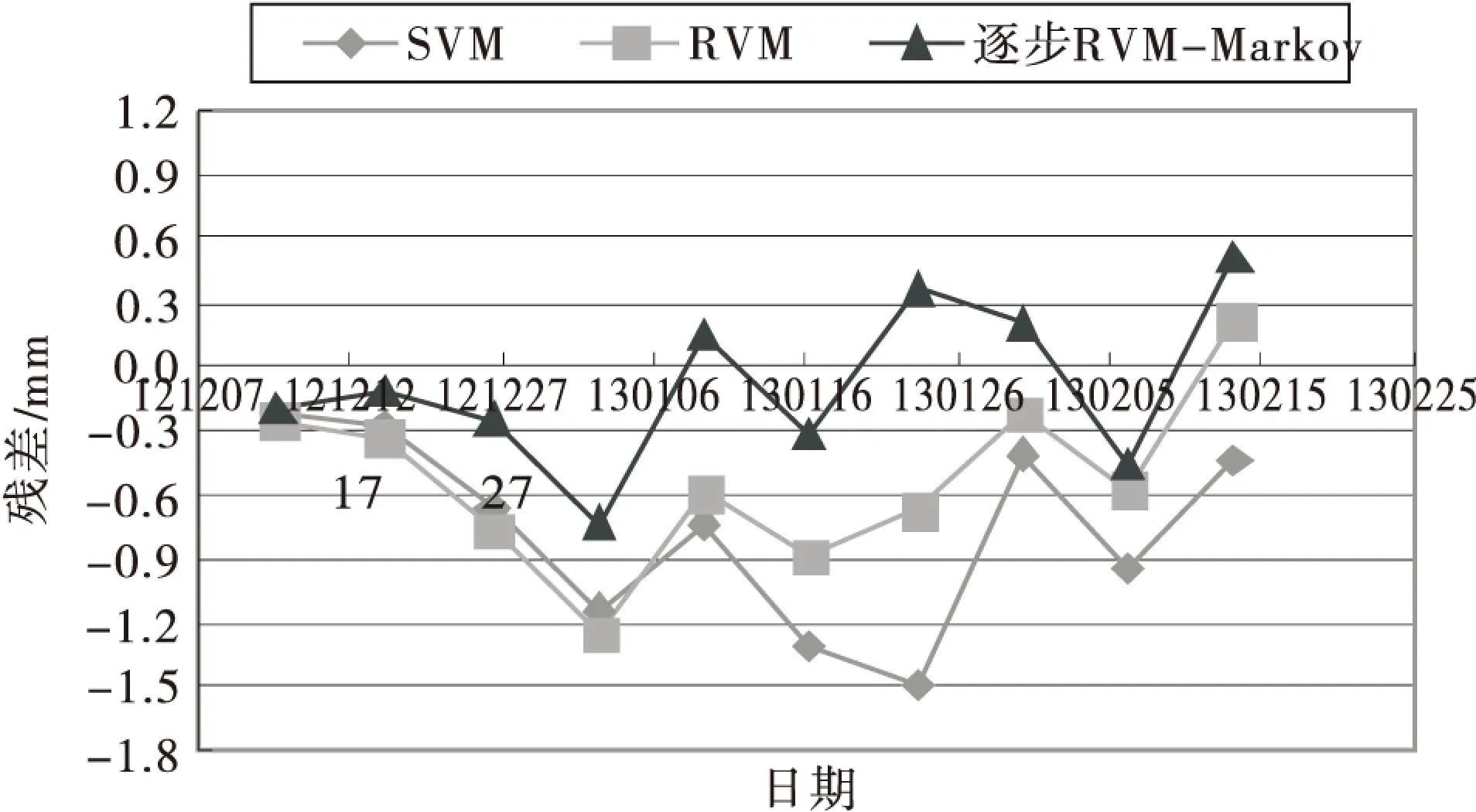
图4　3种模型预测残差曲线图

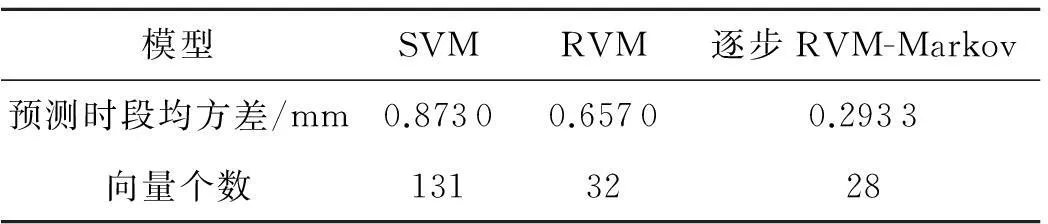
模型SVMRVM逐步RVM-Markov预测时段均方差/mm0.87300.65700.2933向量个数1313228

由图2可以看出逐步RVM-Markov模型的拟合精度较高，同时从图3、4也可以看到逐步RVM-Markov模型预测效果较好，其残差相较于其他两种模型更接近于0，表3的均方差数据也反映出该模型的预测精度要优于其他两种模型．另外根据表3中支持向量与相关向量的个数对比可以得知，SVM模型的支持向量多达131个，而两种RVM模型的相关向量分别为32个和28个，说明RVM模型结构经过稀疏化之后计算的复杂度相较于SVM模型已经大大降低．

5结论

为了弥补SVM模型惩罚系数易选择不当、计算结构复杂等缺陷，将基于贝叶斯框架的RVM模型应用于大坝变形预测，并对残差进行Markov链修正，而且采用逐步更新训练样本的方式以提高预测精度，共同构成了逐步RVM-Markov组合模型．经过工程

实例验证，RVM模型在大坝变形回归预测的应用中拟合精度较高，且经过超参数α的筛选，其结构比SVM更加简化，降低了计算的复杂程度；将Markov链应用于残差修正，有效地提高了预测精度；逐步RVM-Markov组合模型具有相对简单的运算结构与良好的预测精度，在大坝变形监测领域具有良好的应用价值．

参考文献：

[1]顾冲时，吴中如．大坝与坝基安全监控理论和方法及其应用[M]．南京：河海大学出版社，2006．

[2]Tipping M E． Spare Bayesian Learning and the Relevance Vector Machine[J]． Journal of Machine Learning Research，2001(1)：211-244．

[3]王晶．稀疏贝叶斯学习理论及应用研究[D]．西安：西安电子科技大学，2012．

[4]嵇小辅，张孟尧，王博，等．基于相关向量机的赖氨酸反应过程参数软测量[J]．华侨大学学报：自然科学版，2013，34(1)：22-25．

[5]牛东晓，关哲，任峰．等．基于马尔科夫过程的电力企业市场竞争预测[J]．华北电力大学学报，2004(01)：66-68．

[6]张鑫，任永泰，王福林，等．基于改进灰色马尔科夫模型的年降水量预测[J]．数学的实践与认识，2011，41(11)：51-57．

[7]方卫华．基于峰值识别理论的大坝安全监控模型[J]．水电能源科学，2008，26(5)：78-79，149．

[责任编辑王康平]

Application of Progressively RVM-Markov Model to Prediction of Dam Deformations

Tang Qi1,2,3Bao Tengfei1,2,3Du Chuanyang1,2,3Teng Wenwen4

(1. State Key Laboratory of Hydrology-Water Resources & Hydraulic Engineering, Hohai Univ., Nanjing 210098, China; 2. National Engineering Research Center of Water Resources Efficient Utilization and Engineering Safety, Hohai Univ., Nanjing 210098, China; 3. College of Water Conservancy & Hydropower Engineering, Hohai Univ., Nanjing 210098, China; 4. Weihai Municipal Water Conservancy Bureau, Weihai 264200, China)

AbstractThe relevance vector machine(RVM) model has some features including the rarefaction of its construction and the broad range of its kernel function. Thus, using the RVM model to predict the dam deformations has more advantages than using SVM. When we consider that the residual will influence the precision of prediction, the introduction of Markov chain, which can help us correct the predicting data, will enable us to get a highly precise progressively RVM-Markov model. When the RVM is utilized practically, it can have the generalization ability equal with that of the SVM; but it needs much less vectors than the SVM does. Consequently, the process of calculating is simplified; and the Markov chain increases the precision of prediction. Finally. if we use the combined model mentioned above to predict the dam deformations, we will get better results of regression prediction.

Keywordspredicting model for dam deformation;relevance vector machine(RVM);Markov chain

基金项目：国家自然科学基金青年项目(51209078)

收稿日期：2015-06-19

中图分类号：TV698.1

文献标识码：A

文章编号：1672-948X(2015)06-0047-05

DOI：10.13393/j.cnki.issn.1672-948X.2015.06.010

通信作者：唐琪(1991-)，女，硕士研究生，研究方向为水工结构安全监控．E-mail：xqyt77@163.com