电磁源近场测量理论与技术研究进展

黄志洵

(中国传媒大学信息工程学院，北京100024)



电磁源近场测量理论与技术研究进展

黄志洵

(中国传媒大学信息工程学院，北京100024)

摘要：讨论了近场的两类基本电磁环境——束缚场与消失态；前者包含静态场(按r-3规律衰减)和感应场(按r-2规律衰减)；后者包含消失平面波谱，当离源的距离增大时指数地急速下降。束缚场在本文中称为类消失场。近年来两者都发现了电磁波在自由空间以超光速传播的现象，实验上还进一步观察到负波速。由最近几年的实验，对束缚场而言结果并不支持普遍认为的以光速(v=c)迟滞传播的观点；根据对天线近区内无迟滞现象的观测，提供了束缚电磁场的非局域性的实验证据，有的实验甚至达到了高度超光速，即v≥10c。非局域性是一个量子力学概念，故束缚场的非局域特性可能在经典电磁学与量子力学之间建立紧密联系。

在实际应用方面，论述了从辐射近场测量数据转换到辐射远场的技术，包括平面波谱(PWS)法和微波二端口网络散射矩阵法。此外还叙述了与近场微波显微镜发展的有关问题。但本文强调在近场测量中发现的新现象，给出了理论上的多个对偶关系。讨论了近场超光速现象的量子解释，认为应从理论上应用“消失态是虚光子”的思想。本文提出应当重视的一个研究领域是：在不使用反常色散和LHM超材料的近场条件下获得的在自由空间的内向波。最后指出了使用环天线做进一步实验的必要性。

关键词：近场；束缚场；消失态；超光速；负波速；超前波；虚光子

1引言

距离天线小于几分之一(例如1/6)波长的地方是天线的近区(near region)，这里的电磁环境复杂，电磁状态与远区有很大不同。例如很奇怪的，这里会有准恒定场(quasi-steady field)，即类稳场(quasi-static field)，甚至有静电场(electrostatic field)；场表现出电抗性和储能性；场强随距离增大而下降的规律也与远区非常不同。在这里，比值E/H不是常数，波阻抗Z00的概念失去了意义。更奇怪的是，场传播的速度(也可理解为波速)可能比c大得多，而且离天线越近这个速度值会越大。还有令人难以理解的现象，即近区中发现有负波速存在；这不仅威胁到因果性(causality)，而且向天线会聚的波无法解释其来源。所发现的对时间逆行的波(waves backward in time)更给人以莫明其妙之感。……，凡此种种既复杂又激起了研究者的兴趣。

广义的天线概念扩大了研究的领域；实际上，对金属而言，一个小孔、一根尖须、一个凸出物，都有天线的功能和效果，也就有远区、近区之分。在近区，特别要考虑消失场(evanescent field)或称消失波(evanescent waves)的存在，它加大了近场结构的复杂性。虽然我在《截止波导理论导论》[3]一书中已详细论述了消失场(波)的理论，但考虑到激发装置在数学分析上的艰难[4]，分析还是不够深刻的。2008年笔者的论文“论消失态”[5]发表，分析和认识有所深入；但在今天我们还要继续在2013年发表的论文(“自由空间中天线近区场的类消失态超光速现象”)[6]中开始的工作，即把近区场和消失态结合起来研究，并介绍某些相关的应用。

2近场定义和消失态影响[5-7]

在小电偶极子(basic electric dipole)理论中，选用球坐标(r，θ，φ)进行分析，当小天线长度远小于波长(l≪λ)，线上电流分布为等幅、同相(I)，这时由分析可得电场分量

(1)

(2)

这个r值叫特征距离，通常用它作为天线电磁场分区的界线，见表1。在表1中，r≪λ/2π时称为静电场区，其实称“静态场区”(static field region)更确切些，因为通常只把纯粹的电荷场才称为静电场或Coulomb场，而现在天线上的电流是交变的(ejωt)。另外，有时也把表1中的近场区和中场区合称近场区，也有一个称呼是束缚场(bounded field)。与小电偶极子有关的情况见图1。

(a)小电偶极子和球坐标　

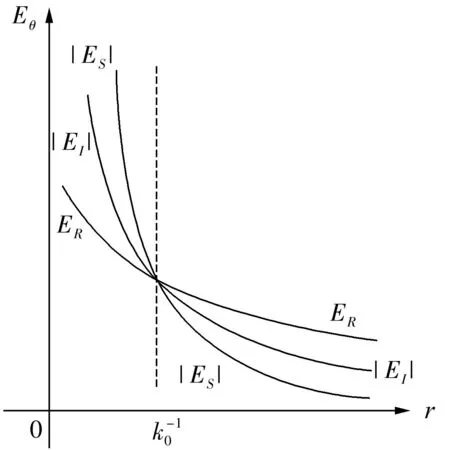
(b)不同类型的场强变化图1

根据电小天线的电磁场定义近区，特点是分区界线(距离)与天线无关，唯一地取决于源的波长——λ的大约1/6距离之内即为近区。

一个任意场源在以波长衡量时的近区和远区的电磁场特性是完全不同的，这为大自然构成的奇妙提供了又一生动的例证。在近区，极其靠近场源的环境中存在最有意思的场，其性质与Coulomb静电场非常相似，称之为“静态场”又有些勉强——首先这里的场源是时变场ejωt的电流，而非静电荷；其次Coulomb场是与距离呈平方反比关系，而这里是呈r-3关系(下降更快)。称呼为static fields(静态场)当然没有问题。离源稍远处也有r-2项，称为感应场。有意思的是这两项均为贮能场，虽有瞬时能量流动但在一个周期中平均值为零。因此能量是由场源周期性地流出，然后又回到场源，不会在系统中消耗掉。……当r用波长度量是很大(r≫λ)时，场变为与传播方向垂直，在场强振幅不变条件下我们由r→∞的极限情况得到理想的平面波，亦即在很远距离上得到横波，即振动方向与传播方向垂直的波。但是，正如J.Stratton指出的那样，在源的附近(即近区)可能有传播方向上的纵向分量，即纵波成份。

表1　电小天线场区划分

如果天线是大辐射器(例如大型抛物面天线)，场区划分方法有所不同；即不仅要考虑源波长λ，近场范围还与辐射器的最大口面尺寸D有关。一种分区方法是，r<λ/2π为天线口径场，r<10λ为电抗性近场，r<2D2/λ为辐射近场(radiative near field)，r>2D2/λ为辐射远场(radiation far field)。大辐射器场区划分见图2。

图2　大辐射器的场区示意　

但是，我们必须建立起更广泛的近场概念。笔者曾指出[6]，天线近区场具有类消失场(evanescent field like或quasi-evanescent field)的特征。消失场具有随距离(r)呈指数下降的特性：

E=E0e-αr

(3)

式中E0为起始点场强，E为距起始点为r处的场强。如α较大，E随r下降很快。实际的电磁结构，出现消失场是常见的，当然其近区场特点非常突出，“远区场”实际上不存在了。为估计近区的r的大小，可考虑取E≤0.1E0，这时有

(4)

若已知衰减常数α的值，可以据此确定近区范围的大小。

图3　偶极天线与近场测量平面　

问题在于如何从理论上考虑和计算消失态(evanescent state)影响。上世纪90年代曾发展近场测量技术，这种平面扫描近场测量技术为确定天线方向图及其参数提供了一条既经济又准确的途径，它的理论基础是场的平面波谱(plane-wave spectrum，PWS)描述方式[7]。天线远场方向图与PWS之间有简单关系；在多数应用中，由近场测量数据经过Fourier变换可得远场方向图。设有一中央馈电的电偶极子天线如图3，取直角坐标系(x，y，z)，原点设在天线中心，而z轴上距原点d处的平面S为近场测量平面。自由空间中若无电荷源(ρ=0)、无传导电流(σ=0)，Maxwell波方程为

(5)

式中k2=ω2εμ；对r≥0的地方有一个解：

(6)

类似地对磁场可导出：

(7)

(8)

(9)

现在可在图3所示的平面作planar scanning，其中d是在近区内。在该平面处有

(10)

式中

(11)

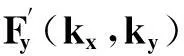
(12)

因而Ey(x，y，0)与Fy(kx，ky)是另一个Fourier变换对；数学说明参见附录。

以上提供了理论基础；由于使用计算机模拟，可用PWS法计算偶极天线的孔隙场分布(aperture distribution)。选择测量平面靠近天线，故消失波包含在近场测量之中。消失态近场行为虽对远场方向图无影响，对于准确建模于近场却重要。上述原理已在实验上有过实证。……另外，有关用近场数据推算远场的详尽说明容后述。

3近场研究的新概念[8，9]

(13)

但在矢量代数中，对任意标量Φ有▽×▽Φ=0，故可取

亦即

(14)

上式也写作

(15)

(16)

(17)

假定电荷源是点电荷q(t)，则可证明解答Φ可表为以下形式：

(18)

而负速度在过去只表示“运动方向相反”而非其值真的为负。如速度值本身就是负的(与矢量方向无关)，则不符合因果性(causality)要求，即因必先于果，而非果先于因。

然而在今天，可以肯定地说上述看法都错了。首先，近年来做成功多个负群速(NGV)实验，证明负速度确实存在[10]。其次，如今对因果性有了更本质的认识，即其根本点在于“果不能影响(反作用于)因”[11]，而不是因必须先于果——量子力学(QM)的发展早已表明这说法并不严格地正确，只是在日常生活中“经典地”正确。总之，Maxwell—D’Alembert方程的超前解不能随便抛弃。

这样，近场研究出现了新情况、新概念。安放在空间某处的源，周围不仅有推迟势的作用，可能还有超前势的作用。这样讲是否有实验基础？回答是肯定的；例如2009年N.Budko[12]在实验中发现近场区的负速度，而且实际上有用的波并非必定以光速c前进；他不仅以实验观测到nagative waveform velocity，而且指出波有可能travel back in time。这些都是过去的教科书中所没有的！……其他实验还多不及备述。

现在我们把上述一般理论分析具体化到简谐电磁场，即时谐波ejωt的情形。这时∂/∂t变为jω，故有以下方程：

(19)

(20)

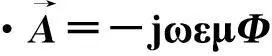
(21)

这时可把D’Alembert方程写作

(22)

(23)

式中k2=ω2εμ；以上两式是Helmholtz方程。是非齐次方程，用于研究包含激发问题在内的电磁场问题。以上两方程的特解为

(24)

(25)

正如前面已讨论过的，这些都属于推迟解(retarded solution)；这种给出答案的方式甚至使人们以为是体现了时间箭头(time’s arrow)，即时间单向性。但这并非对自然规律的完备描述。也就是说，Helmholtz时谐波方程的解必然还有超前解(advanced solution)。

我们把注意集中于标量方程；若空间无体电荷源，常写作下式形式：

(▽2+k2)ψ=0

(26)

式中 ψ是波函数，而上式是无源空间的波幅方程。假定在空间某处放一个点源，在点源外产生的标量势(标量齐次Helmholtz方程的解)一定满足导数连续条件。取球坐标系，并将原点放在点源的位置；从对称性可知势函数仅为坐标r的函数，故以上方程写作

整理后得

(27)

由此得到的解包含两项：①沿r正向朝无限远传播的波，标志符号e-jkr；②从无限远处朝原点方向(即沿r负向)传播的波，标志符号ejkr。通常的做法是舍弃②，理由是“不可能”，或“无物理意义”。但是，在21世纪已过去15年的今天，由于超前波理论重受重视(实验上的标志是负群速实验大量出现)[10]，今后的研究人员必然要考虑“不抛弃第②项”；现今的分析与前面所述内容是一致的。

如果我们沿用习惯的做法，即只承认①的合理性，把微分方程的解写为

rψ=e-jkr

亦即

(28)

因而得到幅度按r-1规律减弱的球面波，即远区辐射场。但这是传统的过于简单化的作法，已不能适应今天的研究工作的需要。总之，对于一个辐射源，矢量电磁场近场、中场动力学远比简单的理解(波以球面波形式向外传播)更为复杂。在源的附近，有时发现波形主体向内行进的现象。因此，波向内传播并非像有的文献所说，只有用左手材料(LHM)构建源天线时才会存在。如果我们上溯到1945年R.Feynman和J.Wheeler的论文，就会明白超前波(advanced waves)思想出现得很早，这与很久以后才出现的LHM无关。超前波也是Maxwell电磁理论的解，只是它会向源聚合集中，甚至在时间上倒运行(黄志洵[8-10]有多篇文章论述这一问题)。当然，过去长期以来未见实证，超前解、超前波的理念未受重视，但今天的情况完全不同了。可以说，近场问题在理论上是复杂的，研究发现会有许多“反常”现象，因此，更加激起了研究者的兴趣。

4近区场与引力场的比较研究

众所周知，通常的电磁理论对离源很近的区域是不加重视的，人们的知识很少。虽然辐射场以光速(c)传播，这一点可以确定；束缚场传播速度如何就不太清楚了。然而大自然的内部充满了许多奇妙的现象之间的联系，例如近区(束缚)场传播与万有引力传播之间有某种可比性；下面是一些理论思考与研究进展。

1687年出版的Newton[13]的划时代著作共有3部分；前面有2个重要的导言，即“定义”和 “运动的公理或定律”。在导言中，Newton提出了关于运动的3大定律。而在第二编Ch.12(“球体的吸引力”)中，提出了万有引力定律。关于后者他的陈述如下：

“推论Ⅲ：一个球相对于另一个球的运动吸引(力)，正比于吸引的与被吸引的球，即正比于这两个球(质量)的乘积。推论Ⅳ：在不同距离处，(引力)正比于该乘积，反比于两球的球心间距的平方”。

在全书的“总释”中，Newton说：“我们以引力作用解释了天体及海洋的现象；所发生的作用取决于它们包含的固体物质的量，并可向所有方向传递到极远距离，总是反比于距离的平方。”但是他又说：“我还不能从现象中找出引力特性的原因，我也不构造假说”。……

Newton的理论像一道强光照亮了中世纪时的蒙昧世界，其作用怎样估计都不过份。正因为如此，笔者在一首诗中写道：“牛顿仍称百世师”！他的理论是人类认识史上的一次飞跃。万有引力定律也称为平方反比定律(Inverse Square Law，ISL)，写作以下形式：

(29)

式中G为Newton引力常数，1998年国际推荐值为

G=6.673(10)×10-11m3/kg·s2

(30)

自ISL提出后的300年来，还没有哪个理论在预言的精度上可与之相比。

如果我们注意到半径为r的球的面积计算公式为

S=4πr2

(31)

则容易理解平方反比规律为何出现在物理现象中；在ISL出现98年后，即1785年，法国物理学家C.Coulomb宣布，他通过实验发现：带同号静电的两球间的斥力与两球中心间距的平方成反比，与各自所带电荷乘积成正比，即

(32)

这是Coulomb定律，它与万有引力定律惊人地相似，启发人们做进一步的比较研究。实际上，Coulomb定律也是ISL。例如，假设引力传播速度是超光速的，Coulomb场(静电场)传播速度是否也比光速快？这是有可能的，国际上也循此途径开展研究，有关成果反过来又会促进引力速度研究。

2000年，墨西哥物理学家R.Tzontchev等[14]使用van de Graaf静电发生器开展研究。两金属球半径10cm，中心间距3m，离地面高度1.7m；使用了尖锐的电脉冲。测量结果是，Coulomb作用的传播速度为v=(3.03±0.07)×108m/s，亦即v=1.0107c，比光速快了1.07%。

R.Sminov-Rueda是西班牙物理学家，2007年他指导完成两篇论文；其一为A.Kholmetskii等[15]的文章“束缚性磁场推迟条件的实验”，此文用环天线(loop antenna)做研究，进行了实验，获得两个超光速数据(v=2c，v=10c)；对此的解释是“近区束缚场的非局域性质”(nonlocal properties of bound fields in near zone)。我们知道，非局域性(non-locality)是量子力学(QM)的重要特性之一，其含义几乎等同于超光速性(superluminality)。因而，这篇论文的观点是意味深长的。

A.Kholmetskii等[16]的另一文章是“近区束缚电磁场传播速度测量”，理论分析计算和实验都更完整。发送、接收天线均为环天线，安装在尺寸大于3m的木桌上。实验给出了v/c与r的关系；在远区(r≥80cm)，v=c；在近区，当r=(50—60)cm，v=4.3c；当r= 40cm，v≅8.2c。结论是，当r<λ/2π，束缚场以超光速传播，表现出明显的非局域性。

2011年O.Missevitch等[17]的论文似为Smirnov-Rueda指导下完成的第3篇对天线近区束缚场的研究，实验技术和方法均有改进。文章给出的一个测量结果是v=(1.6±0.05)c；作者们认为有关工作属于“超光速的电磁波传播物理学”(the physics of EM wave propagation at a speed exceeding c)。

2014年 R.Sangro等[18]的论文 “Coulomb场传播速度的测量”，竟然是从讨论引力传播速度问题开始的。这证明我们的判断正确，即宇宙中的静态(static)或准静态(quasi-static)场具有相似的规律，对它们可作有益的比较研究。作为源(source)的东西亦并非仅对孤立的电荷，而可以是作匀速运动的电子束，亦即以恒定速度移动的电荷，其产生的电场仍是Coulomb场。实验技术复杂而精细，结果中未提供明确的速度数据，但证实了“电子束携带Coulomb场”的想法。

以上文献在时间上涵盖了2004年至2014年，获得的Coulomb场传播速度处在超光速即(1.01~10)c的范围内。有关进展不仅丰富了对近区场的认识，还坚定了“引力以超光速传播”的信心。

5近区场的类消失态性质[3，5-6]

电磁波的时间相位因子是ejωt-γz，其中z是传播方向的坐标(距离)，γ是传播常数(γ=a+jβ，a衰减常数，β相位常数)。对于金属壁均匀柱波导而言，内部电磁状态是有截止现象的场，截止频率ωc=2πfc(下标c代表cutoff)。可以证明与fc对应的截止波长为

(33)

式中h是本征值(eigen value)，上式体现了本征值非零的传输系统的特性。

γ的英文写法是propagation constant；现定义一个参数叫传播因子(propagation factor)：

kz=-jγ=β-jα

(34)

因而传输系统可分为两区域，即表2；由于截止区kz几乎是纯虚数，对应的波矢称为虚波矢(imaginary wave vector)，相应的波叫虚电磁波(imaginary waves)。

表2　波导内的两种电磁状态

不仅如此，两者均随距离增大而迅速衰减，只是规律不同——消失场按e-αr规律，近区场按与r3(或r2)呈反比关系。我们认为在一定条件下两者可以非常接近；取消失场强为

Ee=E0e-αr

(3a)

电小天线的场强为

(35)

等式两边各取自然对数，得

lnE0-αr=lnK-lnr3

故可得

(36)

只要上式满足，两种场的下降完全一样。这虽在实际上不可能(因上式中a与r有关)，但却是两个随r增大而不断减弱的场的有趣比较。

另外，两者都有类稳场(quasi-static field)的特征。在消失场理论中，虽然是时变场，但对于某些结构的分析，竟可把它看成为单独电场的静态场情况(例如截止波导中的TM模式用等效电容器分析处理，TE模式用等效电感处理)。在电小天线理论中，也有类似情况——靠近天线的场会遵循Poisson方程，因而可按静电场去处理。

由于上述种种原因，消失场结构和天线近区场结构中，都发现了超光速传播的现象，从而把我们的神秘感又推进了一步。大自然就这样不断刺激人们的想象，使研究者欲罢不能，充满浓厚兴趣。表3是自1999年以后的20多年来各国科学家在理论上和实验上对消失态电磁场造成超光速现象以及近区电磁场中发现超光速现象的研究成果，跨越非常宽的频段(从短波到太赫)。一种情况是速度值为正时的超光速，这时v≤10c；另一种情况是速度值为负时的超光速，那是一种比无限大速度还大的速度[19]，其含义我们已作过多次论述[8-10]。……需要指出的是，早在1996年Ranfagni[20]即用“消失态的存在”解释某些近区场超光速现象，参见图4。

图4　近区场实验中侧向消失场的示意

表3中的两大部分是相互联系的，也符合2013年黄志洵[6]论文的主题和基本观点。图5是表3中最后一项的示意，即樊京等做近区场实验时的装置，实验设计有创新的内涵。

表3　近年来消失态电磁场和近区场研究中发现的超光速现象

续表

图5　 磁偶极子(环天线)测量系统

对于表3，笔者特别关注一篇论文，N.Budko[12]的文章 “自由空间中电磁场局域负速度观测”，该文从提出一个基本的问题开始：究竟是什么以速度c(299792458m/s)行进?众所周知这个值已被国际计量组织确定为米定义的基础(见P.Giacomo，Metrologia，1984，Vol.20，25)。在考虑实际中广泛采用的电磁脉冲时，有一个问题始终存在：是什么离开了用该速度行进的波阵面(wave front波前)？通常认为是自由空间中的完整电磁波形。然而矢量电磁场的近场、中场动力学比简单的“向外传播”要复杂很多。特别是在紧靠源的地方，波前以光速向外传播，波形主体却向内或反时传播(main body of wavefront appears to go inwards or back in time)，此效应导致自由空间中的超光速结果。

Budko提示的近场电磁现象令人惊奇，例如他展示了几个以时间为函数的近场波形的细节，它们是通过逐步加大与源的距离(r)而获得的。尽管波包的边缘向右移动，内含部分却向左移动，即travels back in time。实验证实了上述的模拟(仿真)计算，实际的负速度区大约为8mm。虽然测量的对时间逆行移动较小，这可用源和接收天线间的相互作用等因素而解释。Budko最后力图对所观测的现象从经典或量子理论作出说明，但是很明显，论文在这方面比较弱。有一个解释是这样的：近场和中间场成分都包含一个额外的关于远场的相对时延。这些相对时延随着离场源距离的增加而逐渐消失。因此辐射场的整体效果由两部分组成：一是通常的以光速向外的运动，二是相对向内的运动。这导致了在近场和中间场中所选择的波形特征的速度明显超出了光速。

笔者认为，近场超光速现象可用消失态理论解释，近场负速度现象可用Maxwell-d’Alembert方程的超前解说明。再加上虚光子理论的帮助，这一切均为可理解的物理实在。然而Budko似乎不熟悉、不清楚这些理论，感到有些茫然是可以理解的。

6从辐射近场数据外推到辐射远场[29-31]

前已述及天线的远场条件是r≫2D2/λ，D是大型辐射器的口面尺寸。这个条件的推导是根据天线孔径上的最大相位相差不超过π/8；推导过程是：先假定有1个小尺寸源天线s发射出球面波，经距离r到达最大孔径D的大型待测天线(此时作接收天线)；由图6所示，中心点O与边缘点A有射线的行程差(Δr)，按三角形SOA，有

(37)

由于r≫Δr，D≫Δr，得近似关系式：

(38)

若Δr→0，则r→∞，表示如要求平面波照射待测天线口面，理论上要求无限大测试距离。实际上只是限制Δr的大小，例如规定Δr≤λ/16，代入上式得到

(39)

这时相应的相位差为β(Δr)=2π/λ·λ/16=π/8。

图6　远区界限值的推导依据　

对于大型口面的发射天线，若源频率较高(波长较短)，2D2/λ会是一个较大的值，建设测试场很不方便。例如D=10m，λ=1cm，则可算出2D2/λ=20000m=20km；这个距离很大，而远区的要求是r≫2D2/λ，故可知由辐射近场数据(在小范围获得)推出远场数据是有很大意义的。从辐射近场测量结果推算出需要的远场数据是早在上世纪60年代就展开研究的技术；在平面扫描中探头作平移，以检测场的幅度和相位，操作过程要保证扫描面与大型天线口面的平行度。那么怎样保证得到的结果可靠？首先要有确切的变换理论，其次要有能处理大量数据的电子计算机。

目的在于用小距离内的实验取代大尺度的实验；或者在小距离范围模拟远场条件(缩距技术)，由近场测试数据计算远场方向图(解析技术)。另有一种外推技术，意思是说可以用平面波散射矩阵为基础，并把天线看成一种比二端口(two ports)网络复杂得多端口换能器(multi-ports transducer)，对空间辐射的每个方向和每一种极化都对应一个输入口和一个输出口。这种换能器把自身体系内的波转换为空间内的平面波角谱(发射天线状态)，或把自由空间的平面波角谱转换为系统内的波(接收天线状态)。因此，天线的诸特性要依靠散射矩阵参数的确定。

图7　电磁波辐射系统示意　

先考虑截面A0处的场；横向场写作

(40)

(41)

Ui=ai+bi

式中Z0i为第i口传输线阻抗；按归一化条件(取Z0i=1)处理，这时可写出

(42)

(43)

(44)

(45)

(46)

(47)

式中上标(+)号代表正向传输，(-)号代表反向传输，下标m表示考虑了不同极化情况。

假定有二端口网络，一口的入射、出射波为a0、b0，另一口为a1、b1，则有

b0包含两部分：反射波S00a0和am透射过来的波，故据图6可写出

(48)

所谓b1现在是bm，故有

(49)

为了加深对以上两式的理解，看两种具体情况。先假设天线用于辐射，电磁波bm向外，故am=0，得

b0=S00a0

(50)

(51)

(52)

(53)

类似方法还可分析处理一个完整的传输系统(包含发射天线、传输空间、接收天线)，这里从略。本节内容已表明可以通过波导模式理论与微波网络相结合而建立起可以从近场数据外推远场的基础。图8是一个实例，抛物面天线口径D=0.3m，频率13.5GHz；曲线中的实线是在远场实测方向图，虚线是口径场分布推出的远区数据；二者基本上吻合一致。

图8　由解析技术算出的远场方向图与实测比较　

7基于受试样品与近场相互作用的近场微波显微镜[7，33-36]

科技发展的一个重要特点是各种新材料不断涌现；如何确定它们的性质，需要采取不同的、在多波段实施的测量手段。对材料的理解正来自对于电磁场和物质相互作用的研究，凝聚态物理中进行测量的新方法得到发展；其中的一个技术是在近场条件下实施测量，这时的电磁环境体现为近区场and/or消失场，它们与被测样品(sample)产生相互作用。所得到的知识弥补了传统远场测量的不足。与材料的光学方法测量相比，微波辐射与物质相互作用的方式更加直接。……以上的叙述简单说明了微波近场扫描显微镜(near-field scanning microwave microscope，NSMM)的由来。

NSMM的一个要素是近场微波探头(探针)，英文为near-field microwave probe(NMP)。在微波技术发展史上，波导技术中有一种小孔耦合，其理论基础由H.Bethe建立(见Phys.Rev.，1944，Vol.66，163)。图9显示利用小孔作NMP的NSMM，图中的平板是金属板，上有小孔，产生近场电磁结构；受试样品放在板子与检测器之间。

图9　用小孔作为探针的NSMM示意　

探针还有多种形式可用，图10显示一些可能的方案；许多近场微波显微镜包含一个类似于次波长触角的特性，即显微尖端，该显微尖端被仔细地审视，几乎达到了对样本的审视程度。该尖端可以用小孔在不透明的屏幕上形成图(9(a))，由削尖的棒子形成的电线或探查隧道显微(STM)尖端图(9(b))，电开放式传输线平端(9(c))，磁性回路图(9(d))；以及使用平行微带线的方案，见图(9(e))。可以看出，设计中采用了微波传输线的各种形式，从波导到微带线。

(a)　　　　　　　　　(b)　

(c)　　　　　　　　　(d)　

(e)图10　NMP的各种方案　

图11是美国Maryland大学研制的扫描谐振腔近场微波显微镜(scanned resonator near-field microwave microscope)，注意探针与受试样品之间的关系(tip/sample interaction)。在一般情况下，尖端或者接触样品，或者保持一个远小于探针尖端特性长度D的间距h；现在场区分为3段：近场(静态场)，中场(感应场)，远场(辐射场)，而远场满足D≪λ≪r。在尖端的近场，电场、磁场结构复杂，场分布取决于尖端几何形状及环境的情况；E/H比值可比377Ω大得多或小得多。这些场不是横场，更接近正交，它们按r-2或r-3规律衰减。近场定义是D≪r≪λ，延迟效应小表示传播速度大。当然，近场状态也可能有消失场(态)，具有虚波数的“波”不会带走能量，而是储存电能and/or磁能；这种状态无论小孔或尖端都会有。因此，在针头作用下的样品所产生的是狭义的近场and/or消失场。

图11　扫描谐振腔近场微波显微镜示意　

NSMM具有很高分辨率，可测纳米级、微米级样品；频带也很宽。美国Angilent公司似有产品；中国计量科学院(NIM)可能要研制这种设备，这为近场测量研究提供了动力。

8近场超光速现象的量子解释

现在我们尝试用量子理论解释近区场超光速现象。传统上，电磁理论工作者和天线工程师不大可能在自己的工作中使用量子力学(QM)；但在近区电磁场研究不断深入而且有新发现时就有这样做的必要。首先应了解，QM的本质在于其非经典性、微观性和非局域性；量子力学和狭义相对论(SR)在本质上并不具有一致性(同一性)。R.Penrose曾指出[37]，EPR论文的“物理实在”贯穿着相对论精神，正确的非局域QM图像与SR之间有本质上的冲突”。……笔者认为，SR与QM之间有根本性矛盾。这不是偶然的，它们实际上代表两种不同的自然观和宇宙观。SR不对微观体系作正面诠释，它在1905年问世时国际科学界还不能认识原子的性质，8年后(1913年)Bohr才提出原子能级的概念。SR理论在提出时即表现为经典性和宏观性，到1935年EPR论文发表时又呈现其局域性[38-40]。可以说，EPR论文与SR论文在本质上一致，因而我们能理解Einstein为什么固执地反对QM——QM的非局域性(non-locality)思维方式正是与SR格格不入的东西。EPR论文是1935年发表的，其局域性原则与SR一致，坚持能量与信息以超光速传送的不可能性，坚持在类空的分离体系(Ⅰ和Ⅱ)之间存在超距作用的不可能性。又用思维实验说明QM是违反局域性原则的，而这正是在QM中分离体系有超距作用的根本原因。

2007年 Kholmetskii等[15，16]声称他们在天线近场实验中“证实了非局域性”，因此对这个non-locality应有更深刻的了解。笔者认为QM的3个本质特征中最重要的就是非局域性，其核心思想就是超光速性。近场实验对非局域性的肯定表示经典电磁理论与量子理论之间有深刻联系，只有同时使用这两者才能使自然现象得到理解和诠释；因此在这里有必要再作阐述。

Einstein对QM的反对态度从1926年开始显露，1935年与B.Podolsky、N.Rosen联合发表论文时达到顶点，而EPR论文后来是从反面促进了科学的发展。该文以SR为思想基础，而SR和EPR都否定超光速的可能。但QM允许超光速存在，并与研究超光速的前提即QM非局域性一致。1985年John Bell说[41]，Bell不等式是分析EPR推论的产物[42]，该推论说在EPR文章条件下不应存在超距作用；但那些条件导致QM预示的奇特相关性。Aspect实验[43]的结果是在预料之中的，因为QM从未错过，现在知道即使在苛刻的条件下它也不会错。可以肯定实验证明了Einstein的观念站不住脚。Bell认为在进退两难的处境下可以回到Lorentz和Poincarè，他们的以太是一种特惠参考系，在其中事物可以比光快。Bell指出正是EPR给出了超光速的预期。……1992年以来有多个超光速实验成功的报道，有的以量子隧穿为基础，有的利用经典物理现象(如消失波、反常色散)。而在2008年，D.Salart等[44]用处于纠缠态的相距18km的2个光子完成的实验证明其相互作用的速度比光速大一万倍以上，为104c～107c；可以说此实验对有关EPR的长期争论作了结论。

多年来，量子超光速性是笔者的主要研究课题之一。1985年我们提出了量子势垒的等效电路模型；1991年我们最早指出截止波导中消失波模有负相速(vp<0)和负群速(vg<0)现象，笔者的专著《截止波导理论导论》获全国优秀科技著作奖。2003年我们用同轴光子晶体进行实验并观测到阻带中的超光速群速，为(1.5～2.4)c。2012年提出量子超光速性(Quantum Superluminality，QS)概念[45]，并建议改造现有的高能粒子加速器以寻找和发现超光速奇异电子。另外，我们多次指出：自2000年以来的负群速实验常以某金属(如铯、钾、铷)的原子蒸汽状态作为受试对象，充分利用激光的高科技特性和手段，从而使之成为具有典型量子光学(QO)特征的现代物理实验，因而极不同于经典性质的物理实验。负群速不仅是超光速的特殊形态，而且普遍具有下述特征：输入脉冲进入媒质前，出口处即呈现输出脉冲峰，因而与经典因果性不同。

消失态中指数下降现象在量子势垒中也存在[45]；这种电磁状态有普遍性，因而具有明显特色——传播方向上波矢大小近似为虚数，几乎没有行波(类似驻波)；是电抗性贮能场；等等。它有静态场特征，但又不完全一样。更奇妙的是，消失态与量子场论中的虚光子(virtual photons)相对应[46]。我的朋友Günter Nimtz教授一直坚定地认为“evanescent modes are virtual photons”。

早在1971年C.Carniglia和L.Mendal[47]发表论文“电磁消失波的量子化”，文中说是“选择利用消失波的虚光子途径来表达场”。1973年S.Ali[48]发表论文“量子电动力学(QED)中的消失波”，文中说“消失波实际上是承载场和源相互作用的虚光子”，又说“消失波将成为一个量化理论的虚粒子群”、“消失场与虚光子场是相同的，这并不是一种模式对模式的同一性。”2006年A.Stahlhofen和G.Nimtz[49]发表论文“消失模是虚粒子群”，文中说多年来基于QED的研究认同消失模与虚光子的一致性，其怪异性质(如非局域性和不可观测性)违反了相对论因果律。2000年G.Nimtz教授曾致函笔者说“只有在引入并考虑QM时，消失模才能得到正确描述和理解；消失模现身为虚光子，但它不能测出”。他又说：“我认为消失模是满足Galilei不变性的，不知你同意否？”

因此，从量子场论(QET)和量子电动力学(QED)的角度看，消失态是虚光子群总体贡献的结果。既然电磁源近场的两个组成部分(束缚场和消失场)是类消失态和消失态，故用虚光子理论作为超近区的超光速现象的解释是有益的。例如Nimtz曾指出，在Feynman型时空图上，虚光子对应的过程是空间距离在变而时间基本不变，这就代表有潜在的极高速度。这与用经典电磁理论研究截止波导时的发现[3]——在截止区相位常数近于零的事实总是指向消失态传播非常之快的状况。我们可以从中有所领悟。

9结束语

本文从理论和应用两方面概述了天线(广义说法是任何电磁源)近区场研究的情况和进展。在实际应用方面，论述了传统的从辐射近场(radiating near-field)到辐射远场(radiating far-field)的数据转换理论，以及近场微波显微镜的发展；由此看出近场研究的重要性，从而知道为什么有许多科学工作者投身于这一领域。……然而，由于自二战时期以来70多年期间有天线工程方面的巨大研究规模和技术进步，多数人只关注远场，对近场只满足于片段的(有时甚至是片面的)了解，造成的结果是近场(特别是非常靠近源的地方)的理论进展缓慢滞后；只是到最近十几年中情况才开始改变。

由本文的内容可知，大千世界丰富多彩，人们的认识也就不能简单化、单一化。想象一下，一个被纯电抗性场紧紧包围的源天线，有功功率(有时是强大的有功功率)却从这种贮能场环境中冲出，在远区形成接近平面波的电磁结构，这难道不是非常生动有趣的场景么？近年来在非常靠近源的地方发现了超光速传播现象和负波速传播现象，这都要求更进一步的更深刻的解释。而把上述现象与纯粹Coulomb场、以及充塞宇宙中的引力场的超光速传播现象相联系，这种比较研究方法给人们带来了更多的启示。

本文给出了多个理论上的对偶关系——束缚场与消失场；推迟解与超前解；正波速超光速与负波速；束缚场传播与引力场传播；辐射近场与辐射远场；模式理论与网络理论；经典电磁学分析与量子理论分析；实光子与虚光子；这些对偶性质的二元化特征正是事物本性的体现。……以下笔者给出对进一步开展研究的几点建议：

首先，本文所述近场、中场、远场的划分方法是根据电(小)偶极子天线的场分析而提出来的。然而，近年来的实验显示，环天线具有方便实验、新现象频发、理论尚待深入的特点[15，28]，非常值得再作研究，并探索相关的超光速现象和负波速现象。

其次，对消失态的研究虽有很大进展[5，50-52]，但要深刻认识和掌握其潜在的特质，仍然是困难的。怎样认识它造成的超光速现象？怎样用虚光子理论分析近场？诸多问题仍然待解。近年来意大利物理学家开展了企图直接观测虚光子的研究[53，54]，值得注意。近场理论研究或许能在量子理论的介入下才能取得突破。

再次，虽然早在1945年J.Wheeler和R.Feynman[55]即指出了Maxwell-Helmholtz波方程的超前解不应随便抛弃，但他们当时也不敢说会有单独的超前波存在。在今天，我们知道确有负速度的波[8-10]。特别是，2009年N.Budko[12]以实验发现了天线近场区的负速度，现象是在自由空间中发生的，并不依靠反常色散之类的媒质。近年来以负物理参数为基础的超材料(metamaterials)理论与技术迅猛发展[56]；在这研究浪潮中也出现了对所谓内向波的研究[57]，却是依靠所谓“异向介质”的，实际上是一种左手材料技术。我们课题组也在2014年成功地测到了负群速(NGV)[58，59]，但也是使用了以左手传输线为基础设计的芯片……然而现在面对的近场测量不一样，它是不依赖上述条件(如反常色散媒质、LHM材料)也会出现的现象，这就更具有研究价值。

总之，我们强调打破思想局限，用此前被认为不可能的方式思考，去认识未知，去理解现象。对未来的发展我们充满期待。

参考文献

[1]Silver S.Microwave antenna theory and design[M].New York：McGraw Hill，1949.

[2]宋文淼等.实物与暗物的数理逻辑[M].北京：科学出版社，2006.

[3]黄志洵.截止波导理论导论(第2版)[M].北京：中国计量出版社，1991.

[4]黄宏嘉.微波原理[M].北京：科学出版社，1963

[5]黄志洵.论消失态[J].中国传媒大学学报(自然科学版)，2008，15(3)：1-19.

[6]黄志洵.自由空间中近区场的类消失态超光速现象[J].中国传媒大学学报(自然科学版)，2013，20(2)：40-51.

[7]Zhang T，Lucas J.The computation of dipole antenna aperture distribution by near-field measurement plane wave spectrum method[A].Proc 3rd Inter Symp on Antenna and EM Theory[C].Nanjing，1993.

[8]黄志洵.影响物理学发展的8个问题[J].前沿科学，2013，7(3)：59-85.

[9]黄志洵.电磁波负性运动与媒质负电磁参数研究[J].中国传媒大学学报(自然科学版)，2013，20(4)：1-15.

[10]黄志洵.负波速研究进展[J].前沿科学，2012，6(4)：46-66.

[11]刘辽.试论王立军实验的意义[J].现代物理知识，2002，1：27-29.

[12]Budko N V.Observation of locally negative velocity of the electromagnetic field in free space[J].Phys Rev Lett，2009，102：020401 1-4.

[13]Newton I.Philosophiae naturalis principia mathematica[M].London：Roy Soc，1687.((中译：王克迪译)牛顿.自然哲学之数学原理[M].西安：陕西人民出版社，2001.)

[14]Tzontchev R，et al.Coulomb interaction does not spread instantaneously[J].14 Oct 2000，arXiv：phys.100100 36Ⅵ[Phys Class-ph].

[15]Kholmetskii A，et al.Experimentsal test on the applicability of the standard retardation condition to bound magnetic fields[J].Jour App Phys 2007，101：023532 1-11.

[16]Kholmetskii A，et al.Measurement of propagation velocity of bound electromagnetic fields[J].Jour Appl Phys，2007，102：013529 1-12.

[17]Missevitch O，et al.Anomalously small retardation of bound(force)electromagnetic fields in antenna near zone[J].Euro Phys Lett，2011，93：64004 1-5.

[18]Sangro R，et al.Measuring propagation speed of Coulomb field[J].arXiv：1211，2913 v2[gr-qc]，10 Nov 2014.

[19]Sommerfeld A.Uber die fortpflanzung des lichtes in dispergierenden medien[J].Ann d Phys，1914，44(1)：177-182.(又见：Brillouin L.Uber die fortpflanzung des lichtes in dispergierenden medien[J].Ann d Phys，1914，44(1)：203-208.)(also：Brillouin L.Wave propagation and group velocity[M].New York：Academic Press，1960.)

[20]Ranfagni A，Mugnai D.Anomalous pulse delay in microwave propagation：A case of superluminal behavior[J].Phys Rev E，1996，54(5)：5692-5696.

[21]Enders A，Nimtz G.On Superluminal barrier traversal[J].J Phys I France，1992，(2)：1693-1698.

[22]Nimtz G.Heitmann W.Superluminal photonic tunneling and quantum electronics[J].Prog Quant Electr，1997，21(2)：81-108.

[23]Wynne K，Jaroszynski D A.Superluminal terahertz pulses[J].Opt Lett，1999，24(1)：25-27.

[24]Wynne K，Tunileling of single cycle terahertz pulses through waveguides [J].Opt Commun，2000，176：429-435.

[25]Ranfagni A.Anomalous pluse delay in microwave propagation：A plausible connection to the tunneling time[J].Phys Rev E，1993，48(2)：1453-1458.

[26]Mugnai D，et al.Observation of superluminal behaviors in wave propagation[J].Phys Rev Lett，2000，84(21)：4830-4833.

[27]Walker W D.Superluminal near-field dipole electromagnetic fields[EB/OL].http：//www.arXiv.Org，1999.

[28]樊京.自由空间磁力线速度测量实验[J].中国传媒大学学报(自然科学版)，2013，20(2)：64-67.

[29]Kerns D M，Daghoff E S.Theory of diffraction in microwave interferometry[J].J R NBS，1960，64B(1)：1-13.

[30]Kerns D M，Plane wave scattering matrices of interaction between a radiating and a receiving antenna[J].J R NBS，1976，80B(1)：5-12.

[31]黄志洵.广义散射矩阵及功率波理论的若干问题[J].凯山计量，1985，(2)：1-15.

[32]林昌禄.天线测量技术[M].成都：电讯工程学院出版社，1987.

[33]Wei T，et al.Scanning tip microwave near-field microscope [J].Appl Phys Lett，1996，68：3506-3508.

[34]Vlahacos C P，et al.Near-field scanning microwave microscope with 100μm resolution[J].Appl Phys Lett，1996，69：3272-3274.

[35]Symons W C，et al.Theoretical and experimental characterization of a near-field scanning microwave microscope[J].Trans IEEE，2001，MTT(Jun)：1-20.

[36]Anlage S，et al.Principles of the near-field microwave microscope[M].New York：Springer，2007.

[37]Penrose R.The emperor’s new mind[M].Oxford：Oxford Univ Press，1989.

[38]Einstein A.Podolsky B，Rosen N.Can quantum mechanical description of physical reality be considered complete[J].Phys Rev，1935，47：777-780.

[39]黄志洵.从EPR思维、Bell不等式到量子信息学[J].北京广播学院学报(自然科学版)，2001，(4)：1-11.

[40]黄志洵.论EPR思维研究[J].北京广播学院学报(自然科学版)，2004，11(1)：27-39.

[41]Brown J，Davies P.原子中的幽灵[M].(易必洁译)，长沙：湖南科技出版社，1992.

[42]Bell J.On the Einstein-Podolsky-Rosen paradox[J].Physics，1964，1：195-200.(又见：Bell J.On the problem of hidden variables in quantum mechanics[J].Rev Mod Phys，1965，38：447-452.)

[43]Aspect A，et al.The experimental tests of realistic local theories via Bell’s theorem[J].Phys Rev Lett，1981，47：460-465.(又见：Aspect A，et al.Experimental realization of Einstein-Podolsky-Rosen-Bohn gedanken experiment，a new violation of Bell’s inequality[J].Phys Rev Lett，1982，49：91-96.)

[44]Salart D，et a1.Testing the speed of“spooky action at a distance”[J].Nature，2008，454：861-864.

[45]黄志洵.论量子超光速性[J].中国传媒大学学报(自然科学版)，2012，19(3)：1-16；19(4)：1-17.

[46]黄志洵，石正金.虚光子初探[A].现代基础科学发展论坛2010年学术会议论文集[C].北京平谷，2010.

[47]Carniglia C，Mendal L.Quantization of evanescent electromagnetic waves[J].Phys Rev，1971，3(2)：280-296.

[48]Ali S.Evanescent waves in quantum electrodynamics with unquantized sources[J].Phys Rev D，1973，7(6)：1668-1674.

[49]Stahlhofen A，Nimtz G.Evanescent modes are virtual photons[J].Euro Phys Lett，2006，76(2)：189-192.

[50]黄志洵.消失态与Goos-Hänchen位移研究[J].中国传媒大学学报(自然科学版)，2009，16(3)：1-14.

[51]黄志洵.消失场能量关系及WKB分析法[J].中国传媒大学学报(自然科学版)，2011，18(3)：1-17.

[52]Fornel F.Evanescent waves—from Newtonian optics to atomic optics[M].Berlin：Springer，2001.

[53]Onfrio R，Carugno G.Detecting Casimir forces and non-Newtonian gravitation[J].arXiv：hep-ph/0612234V1，19 Dec 2006.

[54]Kim W，Onfrio R.Detectability of dissipative motion in quantum vacuum via superadiance[J].arXiv：0705，2895 V1[quant-ph].20 May 2007.

[55]Wheeler J A，Feynman R P.Interaction with the absorber as the mechanism of radiation[J].Rev Mod Phys，1945，17(2/3)：157-181.

[56]黄志洵.电磁波负性运动与媒质负电磁参数研究[J].中国传媒大学学报(自然科学版)，2013，20(4)：1-15.

[57]刘慈香等.异向介质中的内向波[J].中国科学院研究生院学报，2006，23(6)：815-820.

[58]黄志洵，姜荣.量子隧穿时间与脉冲传播的负时延[J].前沿科学，2014，8(1)：63-79.

[59]Jiang R(姜荣)，Huang Z X(黄志洵)，Miao J Y(缪京元)，Liu X M(刘欣萌).Negative group velocity pulse propagation through a left-handed transmission line[J].arXiv.org/abs/ 1502.04716，2014

附：关于Fourier变换对

在高等数学中，积分变换包含Fourier变换、Laplace变换、Hankel变换等。函数f(t)的Fourier变换为

而F(λ)的Fourier逆变换为

f(t)称为F(λ)的象原函数，F(λ)称为f(t)的象函数。

定义方式也可有些变化；例如取f(t)的Fourier变换为

则逆变换为

也有另一种定义方法，取

则有

在工程计算中Fourier变换对有广泛的应用。

(责任编辑：龙学锋)

Recent Advances in the Theory and Technology of EM Source’s Near-field Measurement Study

HUANG Zhi-xun

(Communication University of China，Beijing 100024，China)

Abstract：In this paper，we review the two major types of the near-field EM environments，i.e.the bounded fields and the evanescent state.The bounded fields contains the static field(attenuated by the law of r-3) and the induced field(attenuated by the law of r-2)；and the evanescent state contains an evanescent plane wave spectrum，which is very rapidly attenuated away from the source(exponentially).In this article，the bounded fields was also called the evanescent-state like fields.Recently，in these two situations it has been discovered that the EM-waves travel at superluminal velocity in free space.And furthermore，experimental observation of the free space negative wave velocity was presented.In recent years，based on the several experiments，we can conclude that experimental dataes do not support the validity of the standard retardation constraint(v=c)generally accepted in respect to bound fields.According to the observation of no retardation inside the near zone of the antenna，the experimental evidence for nonlocal properties of bound EM fields is reported.Some of that retardation parameter v for bound fields highly exceeds the velocity of light，i.e.v≥10c.Due to the nonlocality is the concept of Quantum Mechanics(QM)，the nonlocal characteristics of bound fields promise to shed a new light on a possible close relationship between classical electromagnetism and the QM.

In direction of practical application，we review the technology of transfer from the radiating near-field measurement dataes to the radiating far-field.It contains the method of plane-waves spectrum(PWS)and the method of microwave network scattring matrix.We also described the developments of the near-field microwave microscope.But we emphasize the new phenomenon which discovered in the near-field tests，gives several theoretical relations in pair.The quantum explanation can use on the near-field superluminal behaviors and the theoretical study must to use the idea of “evanescent states are virtual photons”.In this paper，the inner waves obtained in near-field of free space are important，especially it don’t needs the anomalous dispersion tests and the LHM meta-materials.Finally，we must use the loop-antenna in near-field experiment in the future.

Keywords：near-field；bounded field；evanescent states；faster-than-light；negative wave velocity；advanced waves；virtual photons

作者简介：黄志洵(1936-)，男(汉族)，北京市人，中国传媒大学教授、博士生导师，中国科学院电子学研究所客座研究员。

收稿日期：2015-12-15

中图分类号：O413.2

文献标识码：A

文章编号：1673-4793(2015)05-0001-18