东亚夏季风降雨的可预报性研究

刘成璟，章向明* ，唐佑民,3

(1.卫星海洋环境动力学国家重点实验室，浙江 杭州 310012；2. 国家海洋局 第二海洋研究所，浙江 杭州 310012；

3. 北不列颠哥伦比亚大学 环境科学与工程系，加拿大 不列颠哥伦比亚省 乔治王子城 V2N4Z9)



东亚夏季风降雨的可预报性研究

刘成璟1,2，章向明*1,2，唐佑民1,2,3

(1.卫星海洋环境动力学国家重点实验室，浙江 杭州 310012；2. 国家海洋局 第二海洋研究所，浙江 杭州 310012；

3. 北不列颠哥伦比亚大学 环境科学与工程系，加拿大 不列颠哥伦比亚省 乔治王子城 V2N4Z9)

摘要:本文根据CMAP(The Climate Prediction Center Merged Analysis of Precipitation)观测资料，使用相关系数和均方根误差，对CHFP2(Coupled Historical Forecast Project, phase 2 )的2个模式对东亚夏季降雨的季节预报技巧作出评价。在完美模式的理论框架下，分别使用基于信噪比的潜在相关系数和基于信息熵的潜在可预报性指标，对该区域主要针对夏季降雨的可预报性作出评价。通过最可预报分量分析(PrCA)，得到季节降雨的最可预报型。将最可预报型投影到海温场，得到了降水最可预报型对应的海温分布。研究发现：相关系数所反映的预报和观测的线性相关程度总体上是低纬度海洋区域比高纬度陆地区域高，而均方根误差反映的则是在海洋区域降雨预报偏离实际值的程度较陆地区域大，预报水平与目前降雨的季节预报水平相符。潜在可预报性估计表明，潜在可预报率存在空间上的变化，从低纬度向高纬度、从海洋到内陆，呈衰减趋势。同时，信号和噪音的分析表明，信号成分占主导作用，形成了潜在可预报率的空间分布格局，暗示了海洋外强迫的重要作用；中国大陆缺少像海洋区域那样明显的外强迫，因此降水季节预报技巧相比热带海洋区域非常有限。海温投影的分析表明海洋的外强迫是东亚降雨季节预报的重要来源。尽管厄尔尼诺本身的复杂性，它对东亚夏季风的重要影响及其与东亚降雨预报之间的遥相关揭示了它们内在的联系。

关键词:东亚降雨；季节预报；潜在可预报性；最可预报成分

0引言

东亚夏季降雨受多方面因素的影响，最主要的包括东亚季风、青藏高原以及厄尔尼诺等。由于东亚季风从海洋带来大量水汽到季风区，因此季风环流对东亚降水有十分重要的影响。东亚夏季风是形成和维持独特的东亚季风气候的主要气候系统。雨带位置的推进和降雨强度的变化，与季风的强度和位置有显著关系，它的年际波动和变率与东亚洪涝等自然灾害密切联系。因此提高东亚夏季风提前几个月的预报水平具有十分重要的意义。青藏高原是该区域重要的大气热量源汇，对我国季风气候影响显著，同时由于高原地形对西南季风的阻挡作用，且具有独特的热力性质，形成高原季风。高原季风建立和撤退的早迟、持续时间、中心位置的偏移和高低压范围的大小，均会造成高原季风和我国夏季风反常，进而影响到东亚夏季降雨形势。

东亚夏季降雨影响因素众多，而且各影响因子具有的复杂性，造成了东亚降水预报的困难性。一方面，目前对部分影响因子的变化规律理解不够，或者变化本身就高度非线性、高度随机性；另一方面，影响因子与降雨的关系及影响机制缺少明确统一的认识。比如虽然研究称降雨量大小与季风强度有关，但基于各自的考虑，东亚季风强度存在不同的指数定义[1]。而提高降雨预报的能力，必须要以上述内容为前提。目前东亚降雨季节预报仍然是季节尺度气候预报的重大挑战。比如耦合模式CFS(Climate Forecast System)和POAMA(Predictive Ocean-Atmosphere Model for Australia)，虽然在预报西北太平洋-东亚(WNP-EA)850 hPa纬向风异常能达到几个月的预报时效，但在预报该区域夏季平均降雨异常时即使是0月的预报时效仍然具有困难[2]。

如何区分东亚降雨预报中不可逾越的障碍部分和模式误差等可以改进的部分，是一个非常值得关心的问题。潜在可预报性的评价正是作了这样的区分，指出了预报技巧的上限，为模式的发展提供了科学的指导。

气象预报领域的可预报性研究可以追溯到上个世纪。20世纪初，便有了通过求解描述大气运动的数学方程来预报天气的构想，随后几十年建立起来的一套数学方程和数值解法取得重大的突破，奠定了目前天气业务预报的基础。然而，预报取得成功的同时，问题也一并显现：非线性系统的混沌特性使得系统对初始条件非常敏感。即使初始条件很小的不确定性都会呈指数增长使预报失效[3]。随着预报的发展，可预报性的研究也不断深入。潜在可预报性(或预报的不确定性)的估计，成为了热点课题。一般认为一个系统有较高的可预报性，则预报的不确定性较小，反之亦然[4]。然而潜在可预报性的精确估计仍然没有统一的意见。

不少研究在完美模式的理论框架下，通过信噪比等衡量了潜在可预报的外部变率和内部变率的相对贡献。但是有研究指出这种方法低估了潜在可预报性。近年来，基于信息论的理论框架形成并应用于潜在可预报性的系统评价[5]。这种理论引入了信息论“熵”的概念，作为不确定性的度量。把潜在可预报性确定为气候态分布和预报分布的某种“距离”。初始条件的引入带来的熵(混乱程度)的减少，这样通过预报就得到了额外的信息。基于方差的方法和基于信息论的方法从不同的方面定量描述了潜在可预报性，集合预报产品为潜在可预报性的研究提供了方便的策略。本文也将采用这些策略，首先对模式的实际预报技巧作出评价；然后分别使用信噪比和信息论的方法对潜在预报率作出评价；并进一步研究东亚降雨的最可预报成分以及可预报性来源等问题。

1模式、资料和研究方法

1.1模式和资料

本文采用的模式数据是耦合历史回报计划的第二代(CHFP2)，它是加拿大气候模拟和分析中心(CCCma)以提高季节气候预报能力为目的发展出来的耦合模式预报系统。CHFP2预报系统在模式上较第一代有了很大的提高。它使用的海洋模式OM4较之前的OM3垂直分辨率有很大提高，并且在次表层加热、跨密度面混合、水平摩擦、输运和扩散的参数化等方面均有改进[6]。CHFP2包含2个版本模式，分别是CM3和CM4。每个模式的集合数均为10。它们海洋分量相同(OM4)，但大气分量分别为AM3和AM4。

模式产生集合成员有多种方法。比如从同一初始条件，通过加随机扰动使得每个集合成员向不同的趋势演进。或者可以从不同的初始条件，即在预报之前的不同时间开始运行。CHFP2产生集合成员的方法是：先从不同的初始状态开始同化运行，得到不同的模式状态，再把这些状态作为初始条件运行得到预报。模式产生了大量的回报结果，即从1979年1月到2010年12月，每天的和每月的大气、海洋中海表温度、降雨、风场等变量的数据。回报结果可以用来估计预报的可信度，为校正和发展业务预报提供了实验平台；还可以用来研究模式的中、长期预报的能力和限制。

模式的网格化：大气和表面场均为2.5°×2.5°，范围90°N~90°S ，0°E~357.5°E，即144×73个网格点。海洋场网格为1°×1°，且每个大气格点单元下的海洋格点单元正好是6个。

CM3和CM4耦合模式反映了海洋对大气的强迫和大气的反馈作用，因而比单纯的大气模式能更好地模拟海洋-大气系统。2个模式均为每天1次，将大气和海洋分量耦合。海洋分量从大气分量接收日平均的表面热量、水和动量通量，运行1 d后，更新日平均海表面温度(SST)返回给大气。

本次研究使用的是32 a(1979—2010年)每月的降雨预报资料。以季节预报为主要研究对象，如夏季，则从5月份开始报6、7、8三月，并取其平均作为季节预报。研究的区域为东亚，范围3°N ~ 53°N ，73°E ~ 135°E，对应25×21个网格点。

本文采用的观测资料是CMAP(CPC Merged Analysis of Precipitation)，其融合了高度计和5种卫星估计每月的降雨资料。在评价模式的实际预报技巧时，所取的时间区间和空间网格均与模式资料相对应。

1.2预报率研究

预报率研究分为实际预报技巧评价和潜在可预报性估计两部分。实际预报技巧衡量的是预报和观测之间的接近程度，通常采用相关系数和均方根误差等方法来衡量。而潜在可预报性是基于完美模式的假设，与实际预报技巧不同，它并不使用观测资料。

信噪比(SNR和STR)是衡量潜在可预报性使用较为广泛的方法。但研究表明它其实低估了真实的潜在可预报性[7]。基于信息论的原理，可以得到更可靠的衡量可预报性的一套直观的方法。

根据信息熵理论，至少有3种衡量可预报性的方法：可预报信息PI，相对熵RE[8]和互信息MI[9]。3种方法各有千秋，都可以作为衡量可预报性的指标。RE和PI衡量单个预报分布的不确定性，均为初始条件的函数。可以证明，PI和RE取所有初始条件的平均都等于MI[10]。在有限维、静态、高斯和马尔科夫系统的情形，3种方法均可得到解析表达式[11]。

1.2.1信噪比与潜在可预报性

信噪比(SNR)方法以前一直被广泛运用于季节预报可预报性的衡量[12]。在季节时间尺度，信号被认为是大气在缓慢变化的外强迫的作用下的响应，如海表面温度SST、海冰等，而噪音是由相对高频的大气变率如天气过程引入。在集合预报中，信号和噪音可以用集合平均的方差和集合成员在所有初始条件上的分布的方差表达，即：

(1)

(2)

通常用SNR和STR衡量潜在可预报性：

(3)

(4)

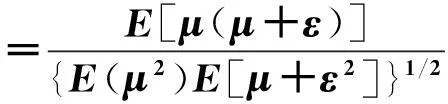
(5)

1.2.2信息熵与潜在可预报性

熵在很多领域都可以作为不确定性的一个自然的而且基本的度量。在可预报性的研究中，熵作为离散度(不确定性)的度量，熵值越大，不确定性越大。连续分布的熵定义为：

H(x)=-∫p(x)lnp(x)dx

(6)

含义为随机变量的平均不确定性。基于信息熵的可预报性方法的核心思想就是：量化气候态分布和预报分布的不同，初始条件的加入(预报)带来额外的信息，不确定性降低，代表可预报性的增加。

假设模式预报某气候变量v，其气候态分布为p(v)。给定初始条件i，产生一个集合预报，这是条件i下的条件概率，记为p(v|i)。从而气候态分布表达式为：

p(v)=∫p(v|i)p(i)di

(7)

相对熵RE和可预报信息PI，根据分布p(v)和p(v|i)熵的两种“距离”分别定义为:

(8)

PI=-∫p(v)lnp(v)dv+∫p(v|i)lnp(v|i)dv

(9)

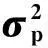
(10)

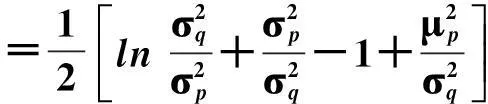
(11)

气候态方差通常是常数，或缓慢的变化，因此PI由预报方差(集合分布)决定。但PI忽略了RE中集合平均μp的地位，而集合平均代表的信号成分，通常被认为是外强迫作用下的响应。对于季节预报来说，信号成分正是可预报性的主要来源。RE中信号和噪音成分的贡献暗示了可预报性的来源：内部动力和外强迫。

另一种潜在可预报性指标，即互信息，定义为[5]：

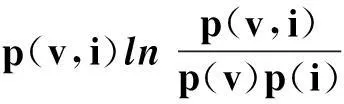
(12)

其中p(v|i)为联合概率分布。当v和i相互独立时，即预报和初始条件相互独立，可预报性消失。当预报和气候态方差是高斯分布，MI可以表示为[12]：

(13)

以上3种方法都可以衡量可预报性。PI和RE衡量的是单个预报的潜在可预报性，是初始条件和预报时效的函数。它们在所有初始条件上的平均值正好等于MI。

关于PI和RE两者的区别，很重要的一点是：RE是绝对差，其值总是大于等于“0”；PI是相对差，其值有可能是负值。一般来说，对模式的预报有一个基本的要求就是不能比气候态差。当PI为负值时，代表了预报比气候态有更大的熵，不符合要求，因此认为是不可预报的。从而用PI衡量可预报性，要求PI必须为正值，这可以解释为预报分布相对于气候态分布复杂程度的减少，显得很直观。另外，当且仅当预报和气候态分布完全相同时，RE是在统计意义上与0没有差别的小值。即用RE来衡量可预报性，预报和气候态的分布如果有统计显著差别时，都代表了可预报。这是否是RE的一个缺点，取决于可预报性更好的定义。还有其他诸如此类的解释，但并不只是有利于一个方法[8]。一个直观的例子，假设预报和气候态分布只在平均值上不同。由于熵相对空间上的平移具有不变性，因此PI将是与0统计上无差别的小值，而RE则是正值[13]。

1.2.3两种方法的关系

气候态方差可以分解为信号方差和噪音方差[14]：

var(T)=var(S)+var(N)

(14)

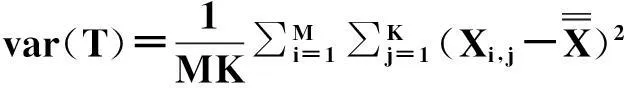
注意到PI和RE均与μq无关，不失一般性，假设等于0。则[5]：

(15)

(16)

(17)

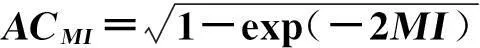
基于SNR的指标仅仅衡量了集合平均μp与观测(假设的一个集合成员)的线性相关部分，而基于MI的指标ACMI则衡量了线性和非线性的两种统计相关，这就解释了基于信噪比的指标低估的部分。当且仅当气候态分布与预报分布都是高斯分布且预报方差为常数时，两者相等[5,15]。

1.3最大信噪比和可预报分量分析(PrCA)

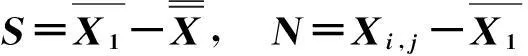
试图寻找一个向量q，把S和N投影到q上，使得SNR最大，即[15]：

rs=qT×S;rN=qT×N

(18)

(19)

根据瑞利商定理，上述最优化问题归结为特征值特征向量问题[16-17]：

qT∑S=λqT∑N

(20)

通过解特征方程

(21)

得到所要寻找的q。因此PrCA也称为最大SNR EOF分析，由ALLEN和SMITH首次引进[18]，通过压缩噪声的影响最优化信号估计。在实际研究中，空间网格点数一般比总的样本数要多，这样求逆过程中遇到并不是满秩矩阵的问题，为此采用截断EOF的方法。与主成分分析PCA不同，PrCA是可预报成分(可预报率)的最优化，而不是要求方差(变率)最大。

2东亚夏季降雨实际预报技巧

本文主要使用相关系数(COR)和均方根误差(RMSE)来评价CHFP2的2个模式的实际预报技巧。

2.1相关系数

相关系数的计算公式为：

(22)

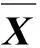
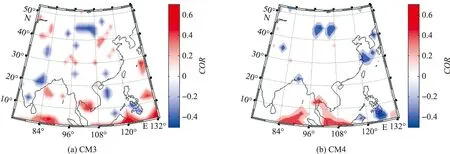
图1　CM3 和CM4的实际预报技巧CORFig.1　The actual forecast skill COR of models CM3 and CM4

先看中国大陆，CM3在中东部、华北地区(30°N~40°N)出现了较大的正相关，达到0.4左右，而CM4在该区域相关较弱，甚至为零，预报水平较低。CM3在华南地区(20°N~30°N)和中国南海的西沙群岛一带(10°N~20°N)出现了负相关，CM4则没有显著的线性相关，实际预报技巧一致较低。再看更低纬度的海洋区域(低于10°N)，2个模式在印度洋和南海都具有较高的相关系数，最高达到0.6。CM3在热带太平洋相关系数较高，而CM4则为负相关。

总体上，相关系数所反映的预报技巧CM3比CM4高。两者都是低纬度海洋区域预报技巧比高纬度陆地区域高。但2个模式相关系数所反映的实际预报技巧非常有限，因为不论是陆地还是海洋区域，并没有出现大范围的较高的相关系数。事实上这与现阶段模式普遍的预报水平相符。

实际预报技巧低，有多方面的原因：首先，对东亚降雨的影响因子认识还不够深入、机制还不够清楚，在模式中未能有效体现。比如青藏高原对东亚降雨的影响不但深刻，而且复杂，其作为东亚地区较大的冷热源汇，积雪、植被等对热收支有十分重要的影响。高原地形独特的热力性质产生高原夏季风，其年际变化伴随东亚夏季风其他子系统变化，通过季风环流的异常变化对中国夏季气候产生重要影响。它与东亚夏季降水的密切关系是不言而喻的。但是由于青藏高原观测资料匮乏，针对高原气候的长期演变和原因以及与东亚季风各系统关系的研究还很少。同时，影响因素本身又高度非线性，加大了数值模拟的难度。CHFP2作为全球模式，注意力更多集中在大尺度环流上，其中没有充分体现出甚至没有体现这些对东亚夏季降水必不可少的过程。

事实上，全球模式在模拟东亚气候均存在较大的局限性。在将全球模式应用于区域尺度气候模拟过程中，由于计算机能力和资源的限制，模式水平分辨率一般较低，如CHFP2仅为2.5°×2.5°的分辨率，难以较好地描述区域地形和中小尺度物理和化学等作用过程。但是随着模式越精细，随之付出的计算代价也大大增加。如何在模式精度和计算代价之间做好权衡是需要考虑的问题。更重要的是还涉及可预报性的问题。分辨率的提高未必能使降水的预报能力得到本质改善，却大大增加了计算成本，后面潜在可预报性评价将会给出理论依据。

前文中介绍模式的时候提到，CM3 和CM4海洋模式相同，而大气模式不同。大气模式的改进并没有为实际预报技巧提高带来帮助，其原因为何，还需要继续进行潜在可预报性的分析。

2.2均方根误差

均方根误差的计算公式为：

(23)

其中：Xi表示预报值，Yi表示观测值，n代表样本数。均方根误差代表的是预报和观测之间绝对差异的大小，值越大表明预报技巧越低。计算结果如图2所示，在中国大部分地区，RMSE反映的预报技巧差异并没有相关系数所反映的那么明显。其它地区，CM4较之CM3在孟加拉国、中国南海等区域有更大的RMSE，暗示了实际预报技巧更低，后文在进行信噪比和潜在可预报性分析时将会作进一步评价。在印度洋区域(孟加拉湾)，2个模式的RMSE均较大，反映了该区域2个模式的预报偏离实际值的程度较大，实际预报技巧较低，关于其可预报性后文也会作进一步的分析。

图2　CM3 和CM4的实际预报技巧RMSEFig.2　The actual forecast skill RMSE of models CM3 and CM4

3东亚夏季降雨季节尺度潜在可预报性

东亚夏季降雨的季节预报技巧受限于多方面的因素，至少包含以下几点：首先是模式方面，模式能否有效地模拟东亚季风系统的主要物理过程，耦合模式对海-气相互作用的描述是否到位等。这方面的不确定性可以通过修改模式的方程、完善模式的参数化等来消除。这要求加深对耦合过程的认识，不断提高模式精度。其次是初始条件的误差。初始场的误差是客观存在的，这受限于当时的技术条件，虽然不能彻底消除，但随着观测手段的逐步提高和同化技术的改善，有望减少这方面的限制。最后是系统的混沌特性和随机过程的强迫，即模式对初始条件的敏感性。随着积分的进行，开始较为接近的初始状态差异逐步拉大，最终的预报分布和随机分布没有两样，即不可预报。这就涉及到可预报时限方面的问题。超过了一定的时限，即使模式再完善，精度再高，预报技巧也无法提高。

基于信噪比的潜在可预报性指标ACp，衡量的是外强迫相对于内部高频噪音的相对重要性；而基于信息熵的指标ACMI衡量的是预报分布和气候态分布之间的差异，这种差异被认为是初始条件产生的预报带来的信息的增加，即不确定性的降低。两者虽然是不同的理论体系，但存在着密切的联系。用信息论的观点来看，气候态分布不含有初始条件的信息，具有原始的混乱程度；若用信噪比的观念来看分布的方差即是“噪音”。预报分布引入了初始条件的区分，其混乱程度降低，熵值发生变化，而预报(集合平均)分布的方差即认为是“信号”。

如图3所示，2个模式中ACMI和ACp均随着空间变化而变化，且变化特征相似，这是因为它们都是基于“信号”和“噪音”。空间变化上，均为从低纬度到高纬度，从海洋到内陆呈衰减趋势。这表明不论是传统的信噪比还是信息熵的理论给出的潜在可预报性评价，都认为热带海洋区域潜在可预报性水平比中国大陆区域高。

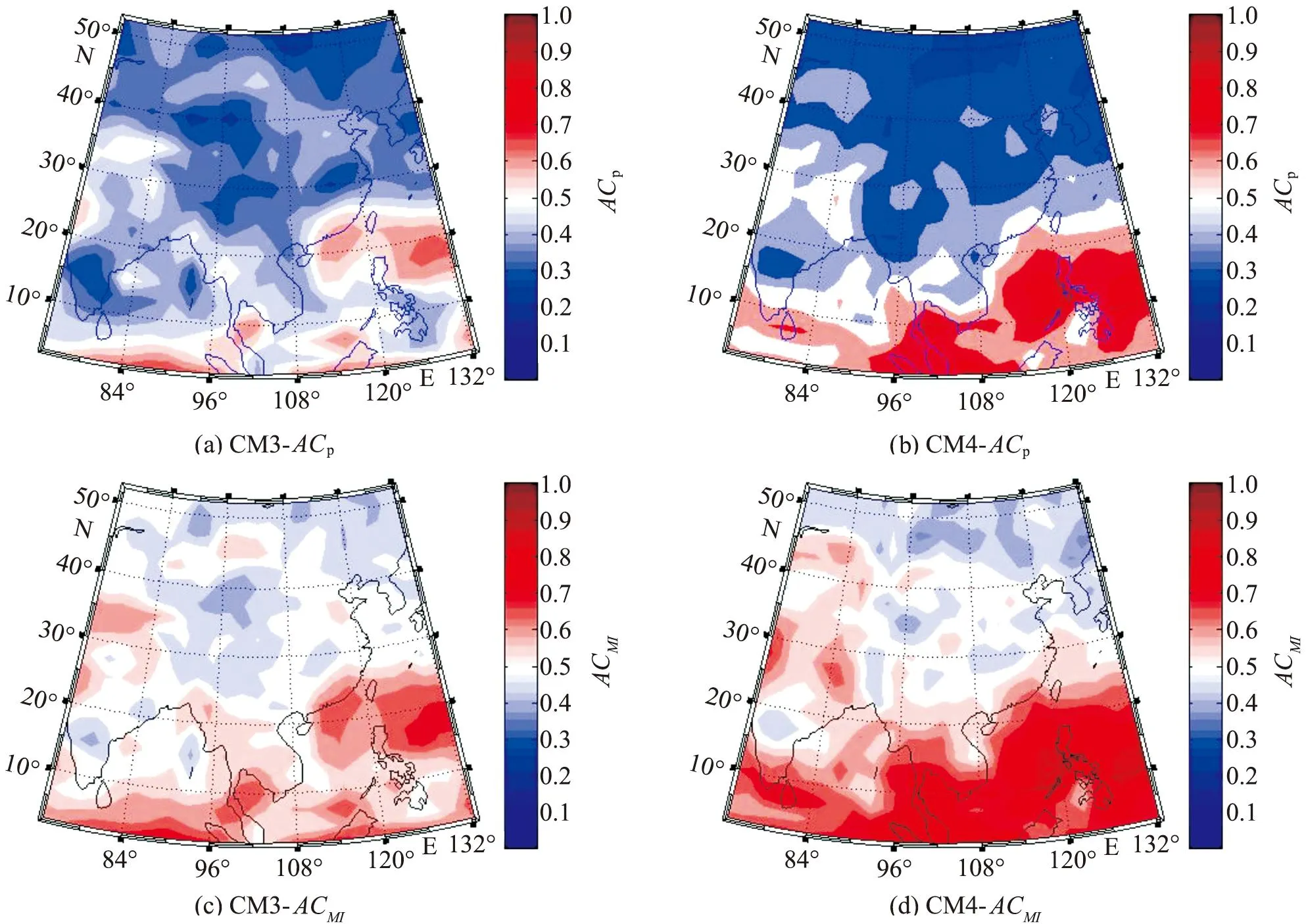
图3　CM3 和CM4的潜在可预报性指标ACp和ACMIFig.3　SNR-based and MI-based potential predictability for models CM3 and CM4

同时两者也存在明显的不同。ACp反映预报和初始信息的线性关系，而ACMI还包括了两者之间的非线性关系。对比发现，在ACp较低的一些区域，用ACMI指标衡量却获得较高的评价。结合式(17)这一点很容易理解：ACMI大于等于ACp，当且仅当预报和气候态分布都是高斯的，且预报方差是常数时取等号。

另外，如图3所示，在南海、西太平洋区域不论是ACMI还是ACp，都一致为高值，而同一纬度的孟加拉湾区域则明显较低，形成“东强西弱”的格局。

因为ACp和ACMI都是基于信号和噪音，通过信号和噪音方面的分析可以有助于理解东亚夏季降雨潜在可预报性估计的结果。如图4所示，2个模式在热带海洋区域，特别是南海和西太平洋区域，均具有很强的信号成分，而在这两个区域噪音则相对较弱。这为上述空间变化的特征给出了合理的解释：在外强迫作用下，预报的分布明显区别于气候态分布，即带来了信号；且预报对初始状态的微小扰动并不敏感，从而噪音较弱。而中国大陆缺少像海洋区域那样明显的外强迫，因此降水季节预报技巧相比热带海洋区域非常有限。

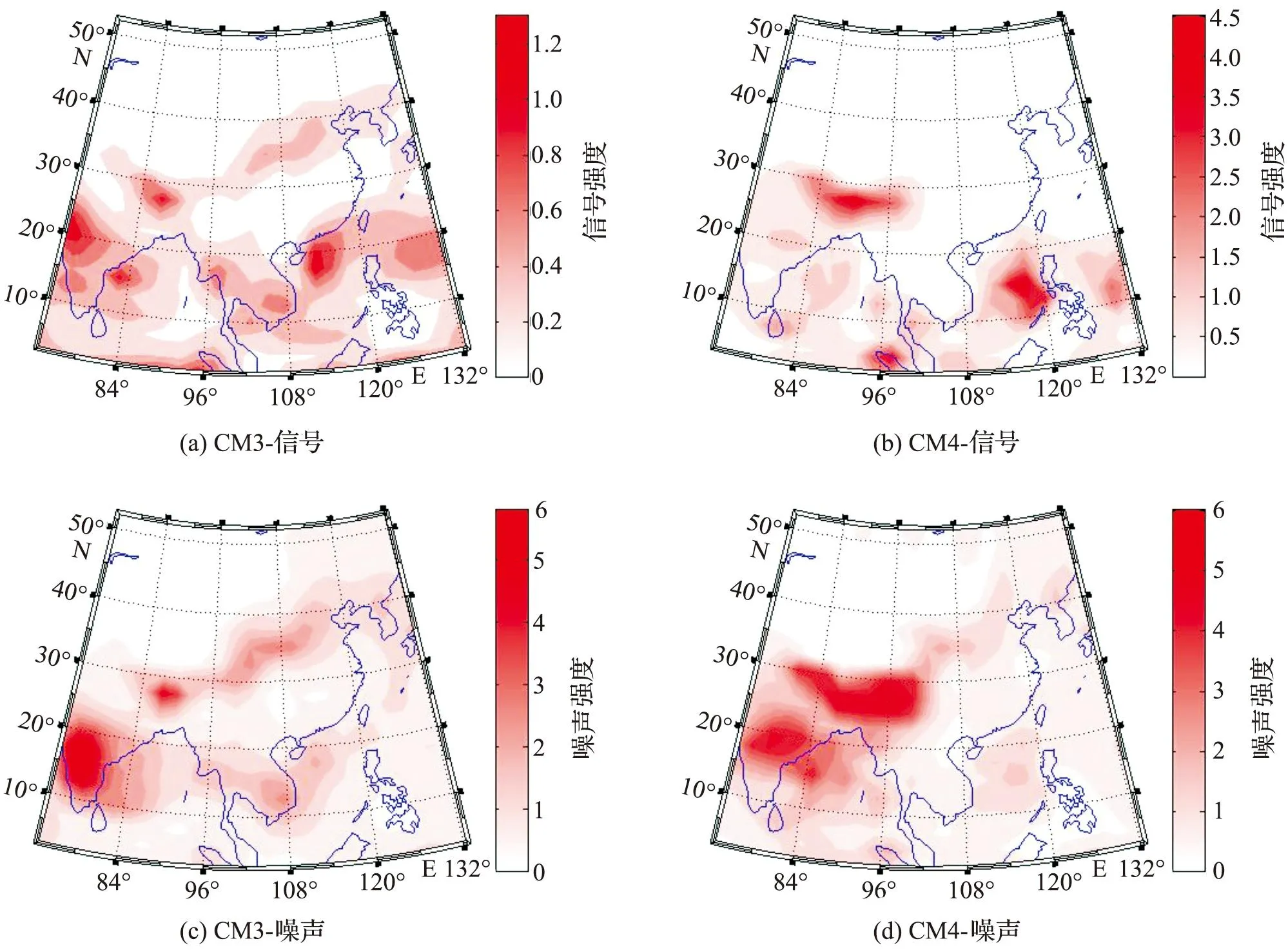
图4　CM3 和CM4的信号和噪音分布Fig.4　The spatial pattern of signal and noise variances for models CM3 and CM4

由图4中的噪音分布可知，2个模式在孟加拉湾区域均具有很强的噪音成分，远高于同纬度的南海和西太平洋区域。而该区域的信号成分相比南海和西太平洋区域又较弱，这两方面因素造成了上述热带海洋区域潜在可预报性“东强西弱”的格局。噪音成分成为限制孟加拉湾区域预报技巧的主要因素，这与中国大陆主要受限于缺少信号成分不同。

信号和噪音的作用，实际上反映的是内部变率和外强迫的相对重要性。根据式(15)，ACMI由信号和噪音方差共同决定。如孟加拉国夏季出现的信号较强，却因为噪音成分比其他季节高出一个量级，而没能得到较高的潜在可预报性评价。一方面在缓慢变化的外强迫作用下，预报的分布明显区别于气候态分布，从而可获得额外的信息；另一方面，预报的轨迹从初始状态一个微小的扰动逐步分离，集合成员之间的差异随着积分的进行而拉大，即不可预报。潜在可预报性估计是考虑了两方面因素的一个综合评价。

2个模式的差异方面，由图4可知，CM3的信号分布在30°N~40°N之间具有带状特征，噪音分布特征与之类似，而CM4不具有这样的信号分布，反而是其噪音分布在对应的区域具有这样的条带。这就解释了在中国中东部、华北地区CM3的预报技巧高于CM4的原因：CM4的大气模式改进，并没有为这里带来更多的信号成分。

另外，在南海和赤道太平洋的海洋区域，CM4的信号则要比CM3强得多，导致潜在可预报性要高。这也暗示了海洋外强迫的重要作用。

随着海-气相互作用研究的不断深入，人们深刻认识到海洋对区域气候的影响。耦合模式把区域气候系统纳入大尺度环流的优势是不言而喻的。潜在可预报性的分析结果则表明，随着对耦合过程认识的加深、观测手段的完善和模式计算精度的提高，热带海洋区域的预报能力将有较大的上升空间；而中国大陆区域则没有这么乐观，即使提高模式精度，模式也难以显示较好的稳定性，预报能力上限较低。

4东亚降雨季节预报的最可预报型

PrCA即最可预报成分分析，是信噪比率的最大化，而不是像主成分分析那样要求解释方差(变率)最大。通过PrCA方法得到最可预报成分和对应的空间型。如前所述，本研究预报目标为夏季，则预报初始时间为5月1号，取6月、7月和8月的平均作为夏季预报。因而在PrCA分析之前季节内变率已被过滤，结果中包含的是年际变率和长期趋势。若要包含季节内变率应当选择每天或者每周的预报资料。

将PrCA前几个空间模与对应的时间系数相乘再求和，可以用来重构预报场。除了前2个模态外，其余更高阶的模态的方差贡献都很小。因此本文只考察前2个模态的空间分布和时间序列，它们代表了可预报的主要特征(解释方差如表1所示)。影响东亚夏季降雨预报的因素很多，内、外部因子共同作用错综复杂。从前面分析来看，夏季信号成分的分布不集中，信号的强度振幅又非常小，而噪音的振幅却较大。同时，夏季风等主导因素往往又以突变的方式完成季节转换，具有很强的非线性特征，这些都是造成夏季预报不同于其他季节的一个重要原因，夏季的季节预报仍然是个挑战。

表1　CM3和CM4的PrCA前2个模态的方差贡献比(夏季)

如图5所示，从空间分布来看，2个模式夏季的空间型均较为复杂，不像其他季节主要集中于热带海洋区域，纬度上分布于10°N~30°N之间(图略)，与其他季节相比，潜在可预报能力存在明显的“北移”。这一点2个模式的结果中有同样的体现。很明显，夏季的外强迫因子使得潜在可预报的能力北移。夏季风在此过程中起着至关重要的作用。而ENSO对亚洲夏季风的2个子系统即南亚夏季风和东亚夏季风的不同影响，分别解释了这2个区域潜在可预报性特征，这是东亚夏季降雨可预报性的主要来源。

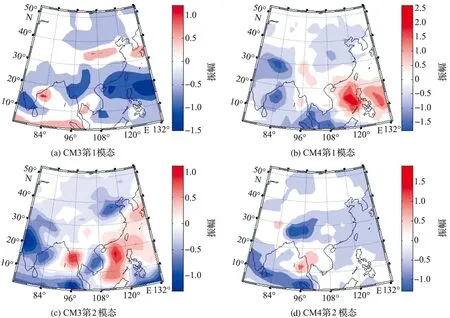
图5　CM3和CM4的最可预报成分对应的空间型Fig.5　The most predictable pattern of PrCA for models CM3 and CM4

CM3的空间型，第1模态正位相(红色)在孟加拉湾和中国大陆的东北、华北地区占有较大比重；负位相(蓝色)在南海、西太平洋占有较大比重。第2模态正位相主要分布在南海、黄海和东海；负位相主要分布在孟加拉湾、西太平洋和中国大陆的东北、华北地区。CM4的空间型，第1模态正位相集中于南海和西太平洋区域；负位相主要分布于孟加拉湾，中国大陆东北、华北地区比重较小。第2模态正位相分布范围很小，负位相集中于孟加拉国和孟加拉湾区域。

前文在评价东亚降雨的实际预报技巧时(图1)，曾提到2个模式在30°N~40°N区域相关系数具有差异，CM4虽然改进了大气模式，但实际预报技巧并未比CM3好。CM3的第1、第2模态在该区域均有较大比重，而CM4前2个模态在此区域比重较小，第2模态几乎没有分布。CM4这样的空间型表明，最可预报成分在30°N~40°N区域占比小，可预报性低。从信号和噪音的比率看，CM4虽然改进了大气模式，但从耦合系统的整体来看，系统对初始条件的敏感性，使得模式随着积分的进行，集合成员之间的差异逐步拉大，造成较大的预报误差方差即引入了噪音，从而可预报性降低。潜在可预报性的研究正是综合评价模式的预报能力上限，为模式的发展提供了科学的指导。

图6是2个模式PrCA的时间序列，显示了显著的年际变率，而长期趋势并不明显，因此反映的是年际变率的潜在可预报性。观察CM3第1模态的时间序列特征，在1983和1998年均出现了极大峰，这些年份正是强厄尔尼诺年。由于PrCA是信号与噪音的比率最优化，峰值代表在强厄尔尼诺年有强降雨信号。并且我们认为具有这样的年际变化特征的降雨为最可预报的。那么该可预报成分与赤道东太平洋的海温异常或许存在遥相关。

同时，CM3第2模态与CM4第2模态的时间序列变化规律十分相似，应当具有某种联系。下面海温投影得到的最可预报型对应的SST异常将印证上述想法。

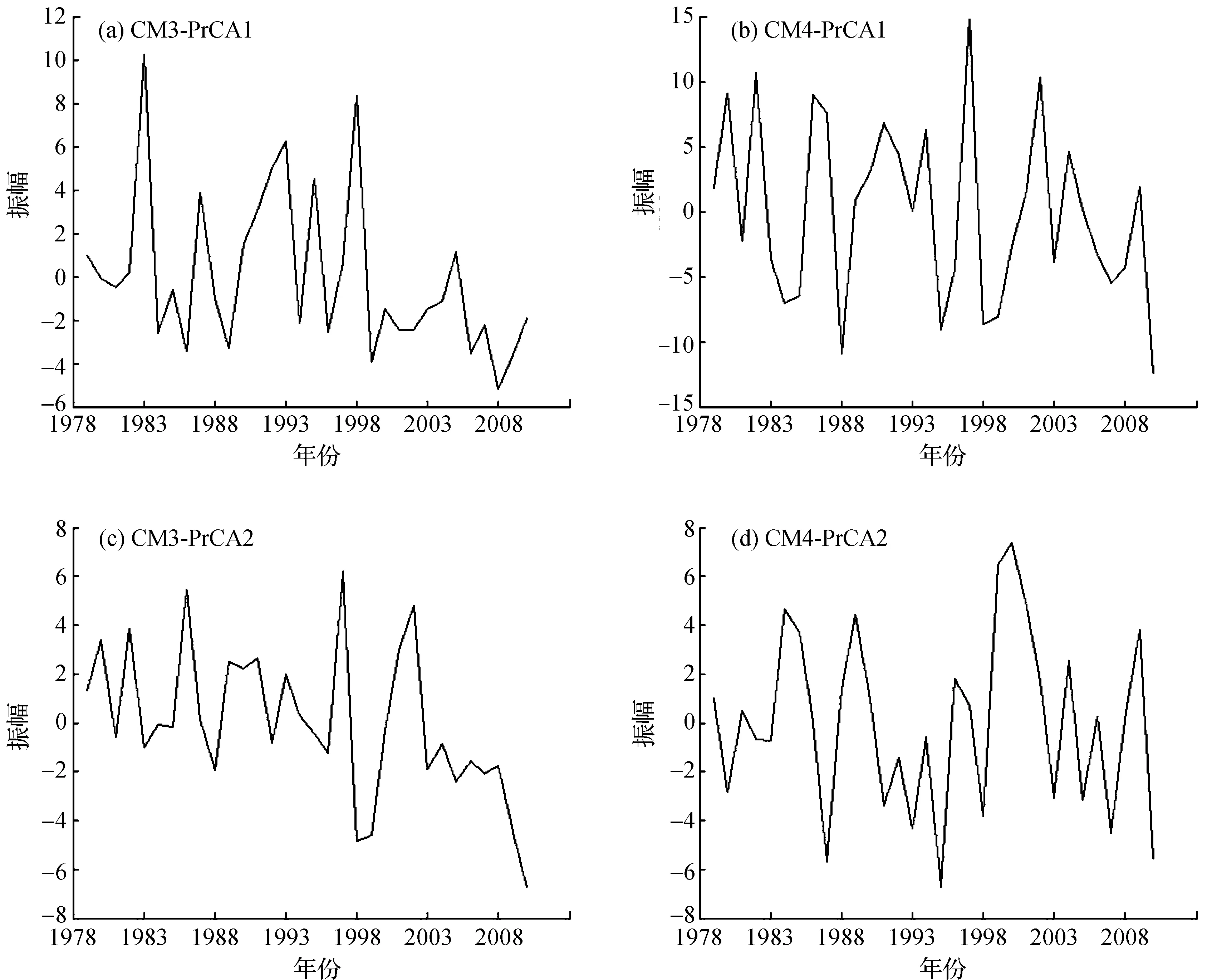
图6　CM3 和CM4最可预报成分的时间系数Fig.6　The time series of PrCA for models CM3 and CM4

东亚夏季风对东亚降雨具有十分重要的影响，而ENSO又是亚洲夏季风季节可预报性的主要来源[15]，本研究试图揭示东亚夏季降雨与赤道太平洋SST异常的遥相关。将PrCA得到的最优滤波算子投影到观测的海表面温度异常(SSTAHadI)，得到最可预报型对应的海温分布(范围：120°E~60°W，30°S~30°N)。图7依次为CM3和CM4的前2个模态的时间序列相对应的SSTA分布。

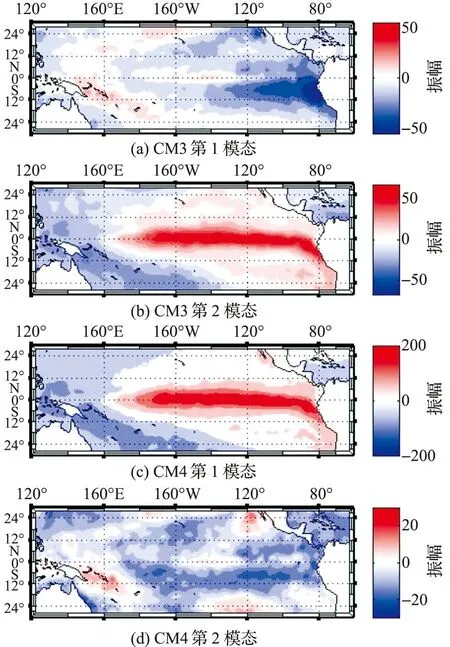
图7　CM3 和CM4的PrCA第1和第2模态对应的海温型Fig.7　The corresponding SSTA pattern associated withthe PrCA mode 1 and mode 2 for models CM3 and CM4

CM3的第1模态对应的SSTA呈现明显的厄尔尼诺结构。CM3的第2模态对应的SSTA和CM4的第1模态对应的SSTA分布结构高度吻合，均为东赤道太平洋冷池明显正异常，且延伸较远。CM3的第1模态对应的SSTA分布和CM4的第2模态对应的SSTA分布较为类似，均为东赤道太平洋冷池负异常，但两者又有一定差异：前者相对集中在厄瓜多尔和秘鲁沿岸，呈现明显的拉尼娜特征；而后者强度较弱，且分布不集中，延伸较远。因此这两种类型的SSTA分布，分别与2个最典型的可预报成分相联系。其中CM3中2种类型比重相近，而CM4中第1种类型明显占主导作用。这说明后者相比前者在大气模式方面的改进，使得该模式在ENSO信号的驱动下，获得很好的稳定性，海-气相互作用更加明显，耦合较强。

SST通常与缓慢变化的外强迫相联系，代表了可预报成分；或者说在缓慢变化的SST外强迫作用下，预报的分布明显区别于气候态分布，从而可获得额外的信息，即潜在可预报性。赤道太平洋SSTA分布和东亚夏季降雨的最可预报成分相联系。东亚降雨对赤道东太平洋SST异常的遥响应，形成了稳定的遥相关型，揭示了ENSO对东亚夏季降雨可预报性的影响。

5讨论和结论

大气和海洋动力系统受非线性或随机外强迫的作用，很大程度上限制了潜在可预报性，即预报的不确定性。此不确定性是动力系统固有的，而与系统的数学表示无关。其主要特征是原本接近的初始状态分离的速率。即使是完美模式，这种不确定性仍然存在，不可能通过完善模式来消除或减轻。因此，潜在可预报性的研究可以探测预报技巧的提升空间，为模式的改进指明方向。

潜在可预报性的精确估计是很有挑战性的课题。近来，通常用信噪比或完美相关系数来衡量潜在可预报性。这种方法存在几个问题：首先，信号是可预报的而噪音不可预报的假设并非总是成立。在某些情况下，噪音可能产生或增加可预报性，如ENSO的可预报性中西风爆发和高非线性的作用。其次，集合平均和集合成员之间的相关性本质上是初始条件和预报之间的线性关系，是广义的潜在可预报性的一个特殊情形，而更直观的潜在可预报性应该是衡量初始条件和预报的相关性(线性或非线性)。因此信噪比事实上低估了真实的潜在可预报性。

本研究中使用了基于信息熵的潜在可预报性指标来研究东亚降雨的潜在可预报性。使用多集合的集合预报产品，详细分析了基于信息熵和基于信噪比的两种方法衡量的东亚夏季风降雨的潜在可预报性。

总体来看，2个模式的潜在可预报性指标ACMI和ACp的特征基本类似。在30°N~40°N的带状区域信号和噪音的分布特征差异，解释了中国中东部、华北地区CM3的预报技巧高于CM4的原因。2个模式PrCA分析结果的对比从另一个方面解释了这一点，CM3的前2个最可预报分量在该区域均有较大比重，而CM4则比重较小，第2模甚至没有分布。但在南海和赤道太平洋的海洋区域，CM4的信号则要比CM3强得多，导致潜在可预报性要高。这也暗示了海洋外强迫的重要作用。

虽然2个模式的实际预报技巧都非常有限，但热带海洋区域还是有较高的潜在可预报性。实际预报技巧过低，主要受限于模式未能有效模拟东亚季风区海-气动力过程以及随机误差的影响。潜在可预报性的分析结果表明，随着对耦合过程认识的加深、观测手段的完善和模式计算精度的提高，热带海洋区域的预报能力将有较大的上升空间；而中国大陆区域则没有这么乐观，即使提高模式精度，受非线性和随机因素的影响，模式难以显示较好的稳定性，预报能力上限较低。

PrCA即最可预报成分分析，是信噪比率的最大化。本文通过分析PrCA得到最可预报成分和对应的空间型，着重研究了东亚夏季降雨的季节预报的可预报性。研究发现：PrCA的模存在空间和季节变化。PrCA的最可预报成分年际变率显著，而长期趋势并不明显。夏季前3个模的方差贡献比总和均低于50%，远低于其他季节，表明了夏季预报系统的复杂性和独特性。并且，夏季的外强迫如夏季风带来的信号成分，使得潜在可预报的能力 “北移”。海陆性质和地理纬度的差异，使得中国大陆缺少像孟加拉湾、南海、西太平洋区域明显的信号成分，甚至在中国西南很大一片区域存在较强的噪音成分，限制了潜在可预报性。

将PrCA分解出的最优滤波算子投影到观测的海表面温度异常，得到最可预报型对应的海温分布。2种类型的SSTA分布，分别与2个最典型的可预报成分相对应。厄尔尼诺本身虽然是非线性的，其作用的内在机制也很复杂，很难将它完全归结为信号或者噪音，但赤道太平洋SSTA和东亚夏季降雨的最可预报成分相联系，揭示了ENSO对东亚夏季降雨可预报性的影响，是东亚夏季降雨的可预报性的主要来源。

由于全球模式在模拟东亚气候时普遍存在的局限性，CHFP2不可避免地也具有水平分辨率低的缺陷。其中没有充分体现出东亚夏季风和青藏高原等对东亚夏季降水必不可少的因素的影响、甚至这些机制还不是十分清楚。在可预报性来源方面也没有体现出这些因素的显著作用。今后应当加强这方面的研究，有望为模式的改进提供可靠的理论依据，为东亚降雨提供更高的预报技巧。

但作为全球模式，CHFP2注意力更多集中在大尺度环流上，对海-气耦合过程的模拟体现出了一定的优势。特别是鉴于ENSO对东亚夏季降雨的预报技巧的支撑，加强模式对ENSO的模拟能力，也将有助于提高东亚降雨预报的能力。

另外，本研究中的分析是基于高斯分布的假设，为的是可以得到MI等的解析表达式，以简化潜在可预报性的计算。高斯分布的假设对于月平均或季节平均的预报是合适的。如果是更短时间尺度的预报，则该假设未必成立。这种情况下，基于信息熵的潜在可预报性计算需要根据概率密度分布进行积分，有一定挑战。

参考文献(References)：

[1] WANG Bin, WU Zhi-wei, LI Jian-ping, et al. How to measure the strength of the east Asian summer monsoon[J]. Journal of Climate,2008,21(17):4 449-4 463.

[2] LEE S S, LEE J Y, HA K, et al. Deficiencies and possibilities for long-lead coupled climate prediction of the western north pacific-east Asian summer monsoon[J].Clim Dyn,2011,36(5-6):1 173-1 188.

[3] SHUKLA J. Predictability in the midst of Chaos: A scientific basis for climate forecasting [J]. Science,1998,282(31):728-732.

[4] TANG You-min, CHEN Da-ke, YANG De-jian, et al. Methods of estimating uncertainty of climate prediction and climate change projection [C]∥SINGH B R. Climate change-realities, impacts over ice cap, sea level and risks. InTech,2013:397-420.

[5] DELSOLE T. Predictability and information theory. Part 1: measures of predictability[J]. J Atmos Sci，2004,61(20):2 425-2 440.

[6] MERRYFIELD W J, LEE W S, TANG You-min, et al. The Canadian seasonal to interannual prediction system. Part 1:models and initialization[J].Monthly Weather Review,2013,141(8):2 910-2 945.

[7] TANG You-min, CHEN Da-ke, YAN X. Potential predictability of Northern America surface temperature part 1: Information-based vs signal-to-noise based metrics[J].J Clim,2014,27(4):1 578-1 599.

[8] RICHARD K. Measuring dynamical prediction utility using relative entropy[J]. J Atmos Sci, 2002,59(13):2 057-2 072.

[9] LEUNG L Y, NORTH G R. Information theory and climate prediction[J]. J Clim,1990,3(1):5-14.

[10] COVER T M , THOMAS J A. Elements of information theory[M].New Jersey: Wiley-Blackwell,2006.

[11] CANE D, MILELLI M. Multi-model super ensemble technique for quantitative precipitation forecasts in Piemonte region[J]. Nat Hazards Earth Syst Sci,2010,10(2):265-273.

[12] TANG You-min, RICHARD K, MOORE A M. Comparison of information-based measures of forecast uncertainty in ensemble ENSO prediction [J]. J Climate,2008,21(2):230-247.

[13] DELSOLE T, TIPPETT M K. Predictability: Recent insights from information theory[J]. Rev Geohpys,2007,45(4):1-22.

[14] KUMAR A, HOERLING M P. Annual cycle of Pacific-North American seasonal predictability associated with different phases of ENSO[J]. Journal of Climate,1998,11(12):3 295-3 308.

[15] YANG D, TANG You-min, ZHANG Yao-cun, et al. Information-based potential predictability of the Asian summer monsoon in a coupled model[J]. J Geophys Res,2012,117(D3):812-819.

[16] SCHNEIDER T, GRIFFIES S M. A conceptual framework for predictability studies[J]. J Clim,1999,12(10):3 133-3 155.

[17] VENZKE S, ALLEN M R, SUTTON R T, et al. The atmospheric response over the North Atlantic to decadal changes in sea surface temperatures[J]. J Clim,1999,12(8):2 562-2 584.

[18] ALLEN M R, SMITH L A. Optimal filtering in singular spectrum analysis[J]. Physics Letters A,1997,234(6):419-428.

林其良,黄大吉,宣基亮.浙闽沿岸潮余流的空间变化[J].海洋学研究,2015,33(4):30-36,doi:10.3969/j.issn.1001-909X.2015.04.003.

LIN Qi-liang, HUANG Da-ji, XUAN Ji-liang. Spatial variation of the tidal residual currents in the coastal area off Zhejiang and Fujian Provinces in the East China Sea[J]. Journal of Marine Sciences,2015,33(4):30-36, doi:10.3969/j.issn.1001-909X.2015.04.003.

Predictability of the East-Asian summer monsoon

rainfall in two coupled models

LIU Cheng-jing1,2，ZHANG Xiang-ming*1,2， TANG You-min1,2,3

(1.StateKeyLaboratoryofSatelliteOceanEnvironmentDynamics,Hangzhou310012,China; 2.TheSecond

InstituteofOceanography,SOA,Hangzhou310012,China; 3.EnvironmentScienceandEngineering,

UniversityofNorthernBritishColumbia,PrinceGeorgeV2N4Z9,Canada)

Abstract:The skills of seasonal forecast of East-Asian precipitation, especially for summer seasons were studied. In the perfect model scenario, the potential predictability of East-Asian precipitation in seasonal time scale using signal-to-noise ratio and information-based indices were commented. The most predictable components and corresponding spatial patterns were also derived by PrCA analysis. The results show that the relationship of forecasts and observations displayed by correlation coefficient is characteristic of higher level in ocean region at low latitudes than in land region at high latitudes. While root mean square error skill shows that forecast diverging degree from observations in ocean region is much more than that in land region. Both agree with the current level for forecast. By estimating potential predictability, it shows that the potential predictability exists a spatial variation and it decays from low to high latitude and from ocean to land region. Further analysis of signal and noise components reveals the important role of marine forcing. The skill of seasonal rainfall is quite limited for lacking of apparent marine forcing in the mainland. By projecting the time series of the leading two modes onto the SSTA field, it shows that the forcing of ocean is the main source of potential predictability of East-Asian precipitation prediction in seasonal time scale. Despite the complexity of ENSO, it is clear that it has great influence on East-Asian monsoon, and the teleconnection between East-Asian precipitation prediction and ENSO may reveal the internal relations of them.

Key words:East-Asian precipitation; seasonal forecast; potential predictability; most predictable component

作者简介:林其良(1989-)，男，浙江台州市人，主要从事近海动力过程方面的研究。E-mail:635860038@qq.com

基金项目:国家重点基础研究发展计划项目资助(2011CB409803)；国家自然科学基金项目资助(41306025)；国家海洋公益性行业科研专项经费项目资助(201205015)

收稿日期:2015-05-25修回日期:2015-07-23

Doi:10.3969/j.issn.1001-909X.2015.04.002

中图分类号:P456.7

文献标识码:A

文章编号:1001-909X(2015)04-0017-13