2个耦合模式中MJO的预报技巧

刘　达，章向明*，唐佑民,3

(1.卫星海洋环境动力学国家重点实验室，浙江 杭州 310012；2.国家海洋局 第二海洋研究所，浙江 杭州 310012;3.北不列颠哥伦比亚大学 环境科学与工程学院, 加拿大 不列颠哥伦比亚省 乔治王子城 V2N4Z9)



2个耦合模式中MJO的预报技巧

刘达1,2，章向明*1,2，唐佑民1,2,3

(1.卫星海洋环境动力学国家重点实验室，浙江 杭州 310012；2.国家海洋局 第二海洋研究所，浙江 杭州 310012;3.北不列颠哥伦比亚大学 环境科学与工程学院, 加拿大 不列颠哥伦比亚省 乔治王子城 V2N4Z9)

摘要:本文使用加拿大气候模拟与分析中心(Canadian Center for Climate Modeling and Analysis,CCCma)的耦合模式预报产品，应用以信息论为基础的可预报性理论框架，诊断、分析了耦合模式中Madden-Julian Oscillation(MJO)的预报率，包括实际预报技巧和潜在预报率，以及热带季节内尺度变率(Intraseasonal Variability,ISV)最可预报模态的空间分布。并在此基础上讨论了不同时间尺度平均对MJO预报技巧的影响。结果表明:本文使用的2个耦合模式中，MJO的预报技巧与目前全球主要使用的预报模式相近，约为10 d。潜在可预报技巧可以达到30 d以上。随着时间尺度从日平均增加到10 d平均，MJO的实际预报技巧与潜在可预报技巧都相应提高，尤其是潜在可预报技巧的提高更加显著。进一步分析发现，影响实际预报技巧的一个重要因素是初始条件MJO信号的强弱，当MJO信号很强时，预报技巧较高，反之则较低。本文最后分析了模式中ISV最可预报模态的空间分布，并讨论了如何利用这种最可预报空间分布提高ISV的实际预报技巧。

关键词:MJO；预报技巧；潜在预报率；最可预报模态

0引言

Madden-Julian Oscillation(MJO)是热带低频30~90 d振荡，是大气中最重要的低频振荡现象之一[1-2]。它起源于热带西印度洋，向东传播，在东印度洋和西太平洋上空达到最强，过了国际日期变更线后减弱，但有时会在热带大西洋加强。MJO在传播过程中伴随着强烈的积云对流活动，给热带印度洋和西太平洋带来强降水。同时MJO带来的强风对热带印度洋的动力过程有显著的驱动作用，比如在热带印度洋激发赤道开尔文波并造成东印度洋的季节内变化[3]；MJO还影响热带气旋的生成[4-7]、亚洲季风系统的爆发及季节性雨季和旱季转换[8]。我国研究人员比较关注的是MJO对南海夏季风爆发的影响及MJO引起的南海(东亚)夏季风活动异常[9-11]，以及MJO对ENSO事件爆发的调制作用[12-15]。此外，MJO和北大西洋涛动(North Atlantic Oscillation,NAO)也有密切关系[16]。MJO影响热带及热带以外地区不同时间尺度的大气和海洋现象，同时也是热带地区季节内变化可预报率的主要来源[17]。对MJO的有效预测不仅有助于更加清楚地了解MJO本身的发展过程，而且可以填补天气预报与季节预报之间的空缺[18-19]。综上所述，对MJO的预报不仅对印度洋区域有重要意义，对研究全球天气和气候变化也有重要意义。

近年来，MJO的模拟和预报已得到了国内外学者的极大关注，并取得了显著进步。目前全球通用模式对MJO的预报技巧普遍可以达到2周左右[20]，在MJO比较活跃的北半球冬季，模式对MJO的预报技巧可以达到3周[21-22]。

利用环流模式(General Circulation Model,GCM)对MJO的预报还存在一些限制因素[22-25]，比如积云参数化方案的缺陷[26-28]，粗糙的网格分辨率[23,29-30]以及缺乏对海-气耦合过程的模拟[31-32]等。除此之外，利用数值模式对MJO的预报还受到由观测带来的初始条件的误差和同化系统误差的影响[33]。

现有模式对MJO的预报还需要进一步改进，那么模式可以改进的空间有多大，预报技巧的极限是多少，这些问题都需要通过对潜在预报率的研究来回答。大气海洋系统的可预报率主要受到2个因素的限制：第一是由随机因素和非线性因素造成的影响，由此造成的预报误差和不确定性是耦合模式固有的，不可消除；第二是受到耦合过程认识的局限性、模式和观测的误差或者计算资源的局限性等因素影响造成的预报不确定性，这种不确定性可以随着预报能力的提高而减小。潜在预报率的研究正是为了区分这2种误差。基于完美模式假设，WALISER et al[34]利用大气环流模式(Atmospheric General Circulation Model,AGCM)对MJO的潜在预报率进行了分析，发现模式的降水场中MJO的潜在可预报技巧约为10~15 d，而纬向风场中的潜在可预报技巧可以达到25~30 d。但是由于大气模式缺乏重要的海-气耦合过程，因此对MJO的潜在可预报技巧的计算还存在较大误差。PEGION et al[35]发现耦合模式中MJO的潜在可预报技巧更高，可以达到45 d。目前，已经有很多学者利用不同的模式考察了MJO的潜在可预报率，但是这些工作大多是分散的，缺乏全面和统一的评估标准，因此NEENA et al[36]利用8个耦合模式(如澳大利亚气象局海气耦合模式ABOM1、ABOM2，NCEP耦合模式CFS1、CFS2等)，在信噪比框架下进行了关于MJO潜在预报率的分析，发现耦合模式中MJO的潜在可预报技巧可以达到35~45 d。目前模式的实际预报技巧与之相比，还有相当大的提升空间。

本文使用加拿大气候模拟和分析中心(CCCma)的2个全球耦合模式预报产品对MJO的预报率进行了系统分析，增补了目前MJO预报率评价的模式成员，完善了系统研究MJO预报率的工作。特别指出的是，目前潜在预报率研究主要依赖于传统的信噪比框架。然而，已有研究表明，信噪比估算的潜在预报率低于真实的潜在预报率[37]。因此，本文既考虑了信噪比，同时也利用了以信息论为基础的可预报性理论框架，估算模式中MJO的潜在预报率,并进一步分析了模式中热带季节内尺度变率(Intraseasonal Variability, ISV)最可预报模态的空间分布。这些工作为进一步提高MJO的预报能力提供了科学依据。

1资料和方法

1.1资料

本文使用的850 hPa(U850)和200 hPa(U200)纬向风场数据为NCEP/NCAR所发布(http:∥apdrc.soest.hawaii.edu/data/data.php)，时间跨度为1975—2011年，分辨率为日平均的再分析数据。对外长波辐射(Outgoing LongwaveRadiation,OLR)数据为NOAA发布的同时间段的日平均再分析数据。这些数据空间分辨率均为2.5°×2.5°。用于衡量本文计算的MJO指数(RMM)准确性的标准是由澳大利亚气象局提供的，利用实时多变量计算的RMM(http://www.bom.gov.au/climate/mjo/)。

本文使用的预报产品为CCCma耦合预报计划第二阶段(the Second Phase of Canadian Historical Forecasting Project,CHFP2)第三代全球耦合气候模式(the Third Generation Coupled Global Climate Model,CM3)和第四代全球耦合气候模式(the Forth Generation Coupled Global Climate Model,CM4)的集合预报产品。CM3和CM4的初始条件均为1979—2010年每月1号，包含10个集合成员，模式向后预报365 d。模式集合成员是利用NCEP/NCAR再分析数据积分4个月以后得到，第1个成员超前初始时刻12 h，第2个成员超前24 h，每个成员间隔12 h，以此类推，第10个成员超前5 d。

CM3和CM4的海洋模块相同，是CCCma的第四代海洋模式(the Forth Generation Ocean General Circulation Model,OM4)，大气模块分别为第三代AGCM(the Third Generation Atmospheric General Circulation Model,AGCM3)和第四代AGCM(the Forth Generation Atmospheric General Circulation Model,AGCM4)。

AGCM3利用频谱变化方法来描述水平空间结构的主要变化，垂向利用混合矩形有限元坐标[38]。AGCM3的垂向高度为50 km，分为32层。地表过程模拟使用了VERSEGHY et al[39]提出的3层土壤方案。潜热和动量交换采用了ABDELLA 和MCFARLANE[40]提出的方案，即当表面浮力通量向上时，增加了垂向的热量和水汽混合，从而保证混合层可以达到理想的高度。对流参数化方案采用了ZHANG和MCFARLANE[41]提出的方法，其中包含了对贯穿对流的模拟。

AGCM4在AGCM3基础上进一步发展，AGCM4的垂向结构与AGCM3相似，但对流层的分层更加密集。AGCM4的物理过程参数化方法使用了关联k分布模型[42-44]。辐射传输使用了McICA方法[45]，辐射传输方案中考虑了气溶胶引起的直接或间接的辐射效应，并且增加了硫循环[46-47],以及基于LOHMANN和ROECKNER[48]方法的云微物理方法。

OM4垂向使用了Z坐标，水平向为荒川B型网格。OM4垂向从表层以下10 m到400 m共分为40层，其中16层位于200 m以上。水平方向的球面网格间距经向约为1.41°，纬向约为0.94°。OM4中利用傅里叶滤波抑制由于网格收敛在北极导致的计算不稳定性，并在北极集中建立一列特殊的示踪网格[49]。模式的垂向混合使用了LARGE et al[50]提出的KPP(K-profile parameterization)方案，并向其中加入了能量约束，底部加强了垂直示踪扩散系数用以代表潮汐的混合作用[51]。水平摩擦使用了LARGE et al[52]提出的各向异性粘度参数化方案。

本文采用的模式预报数据变量为U850、U200和OLR。预报数据需要去掉季节循环。由于预报数据的初始条件是不连续的，需要利用观测数据与预报数据结合，去掉预报数据的前120 d平均。最后进行标准化[24]。

1.2方法

1.2.1实际预报技巧

本文主要利用相关系数(Correlation,COR)和均方根误差(Root Mean Square Error,RMSE)来定量评价MJO的实际预报技巧。

COR的定义为：

COR(t)=

(1)

RMSE的定义为：

RMSE(t)=

(2)

其中：RMM和RMMp分别是观测与预报得到的MJO指数，PC1和PC2是联合经验正交函数分析(Empirical Orthogonal Function,EOF)得到的前2个时间序列，N为样本数，下标p表示为预报值。COR主要衡量了预报产品相对于观测位相预报的准确性，COR越大，位相预报的准确度越高。RMSE衡量了预报与观测振幅之间的差异，RMSE越小，预报的振幅越接近观测。

1.2.2潜在可预报率

(1)信噪比

信噪比(Signal-to-Noise Ration,SNR)是一种已经被广泛应用的潜在预报率衡量指标。在季节尺度上，信号被看成是大气对一些缓慢变化的外界强迫，例如海表温度、海冰等要素的响应，噪声则是对更加高频的天气过程的响应[15]。在集合预报中，信号(Signal,S)和噪声(Noise,N)的大小可以近似地通过集合预报来估计[53-55]，即:

(3)

(4)

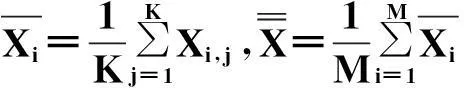
(5)

通常用来衡量潜在预报率的指标主要有SNR和信号率(Signal-to-Total Ration,STR)，即

(6)

(2) 信息熵

熵是一个衡量系统混乱程度的物理量，可以通过p(x)的连续分布计算得到，即:

H(x)=-∫p(x)lnp(x)dx

(7)

基于信息熵衡量潜在预报率的指标主要有相对熵(Relative Entropy,RE)和预报信息(Predictive Information,PI)等。这些基于信息熵的指标的中心思想是使用预报的概率密度与气候态的概率密度之间的差来度量预报不确定性的大小。

假设v是某一大气(海洋)变量，它的气候态分布是p(v)。对于给定的某一初始状态i，v的预报能用它的条件分布p(v|i)表示。因此，RE和PI可以被定义为：

(8)

PI=H(v)-H(v|i)=-∫p(v)ln[p(v)]dv+

∫p(v|i)ln[p(v|i)]dv

(9)

RE和PI是v的预报分布与气候态分布的相对差和绝对差。RE表示为用气候态分布p(v) 代替预报分布p(v|i) 的信息不充分性。PI右端第一项是气候态分布的熵，衡量没有任何观测和模式提供的其他信息时预报的不准确性；第二项是预报分布的熵，衡量引入观测和相关预报后的不确定性。如果RE和RI越大则意味着由于预报提供的有效信息使得引入观测或预报后的不确定性减小程度越大，因此潜在预报率越高[56]。

当气候态分布和预报分布都是正态分布时，RE和PI可以通过变量的均值和方差计算得到[56]：

(10)

(11)

RE和PI是衡量单个预报量的潜在预报率的指数。所有初始条件下的RE和PI的平均值被证明与另外一个统计量——相互信息量(Mutual Information,MI)相等[57]，即：

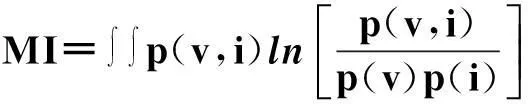
(12)

其中：p(v,i)是v和i的联合概率密度分布。由于与全初始条件下的RE相等，因此通过衡量气候态分布与预报分布的差别或者以初始状态i与未来状态v的统计相关性来计算潜在预报率是2种等价的方法[57]。若预报分布和气候态分布都是正态分布，那么:

(13)

(3) 可预报成分分析

可预报成分分析(Predictable Component Analysis,PrCA)是类似于传统的主成分分析(Principal Component Analysis,PCA)的一种分解潜在预报率的方法。PCA将总方差分解到不同的特征向量，PrCA是将全部潜在预报率分解到不同的成员中，每个成员对潜在预报率的贡献不同。在分解潜在预报率的过程中，如果有少数成员占主导地位，使用PrCA可以让我们只关注具有较高贡献率的成员，从而得到最可预报的空间分布。

理论上，在集合成员数无限的情况下，S和N是相互独立的，但是实际过程中成员数往往是有限的，所以对S的计算往往会受到N的影响。因此，潜在预报率的最佳状态是SNR最大。寻找一个向量q，使得S和N投影到这个向量以后得到的方差最大，即：

rs=qT×S;rN=qT×N

(14)

(15)

根据瑞利定理，上式的最优解可以转化为

qT∑S=λqT∑N

(16)

其中:λ为特征向量；∑S和∑N分别是S和N的协方差矩阵[59-60]，因此PrCA也被称为最大信噪比EOF分析，最初是由ALLEN和SMITH[61]引入用来去除N对S计算的影响，现在已经被广泛应用于潜在预报率的研究[62-63]。

在实际计算中，由于格点的个数比样本数多，得到的∑N通常不是满秩的，所以PrCA采用截断PCA的方法使得特征向量的协方差矩阵满秩。本文选取了PCA的前30个模态。本文主要关心的是PrCA得到的模式中ISV最可预报模态的空间分布。

2MJO信号的提取

为了考察模式中MJO的预报技巧，首先需要利用观测数据计算并得到相应的MJO空间分布。本文计算的方法是基于WHEELER和HENDON[64]提出的方法(WH04)，即利用15°N~15°S范围内OLR、U850以及U200进行联合EOF分析。方法如下：首先将观测数据去掉时间平均以及前3个谐波，滤除季节循环；然后去掉前120 d的平均，从而可以有效地去除与ENSO有关的年际变化以及时间尺度更长的变化；经过上述处理的数据再进行纬向平均去掉纬向变化；为了保证上述3个变量在联合EOF中具有相同的方差贡献，将3个变量分别进行标准化；最后进行联合EOF分析[64]。

图1是OLR、U850以及U200三个变量的联合场进行EOF得到的前2个模态的空间型，2个模态对应的方差贡献率分别为13.36%和12.26%。2个模态都表现出MJO全球纬向1波的特征， U200与U850的反位相关系可以看出大气中的斜压结构。在EOF的第1模态(EOF1)中，纬向风场在0°和150°E附近发生变化，风向的变化有利于增强大气对流。EOF的第2模态(EOF2)与EOF1近似正交。

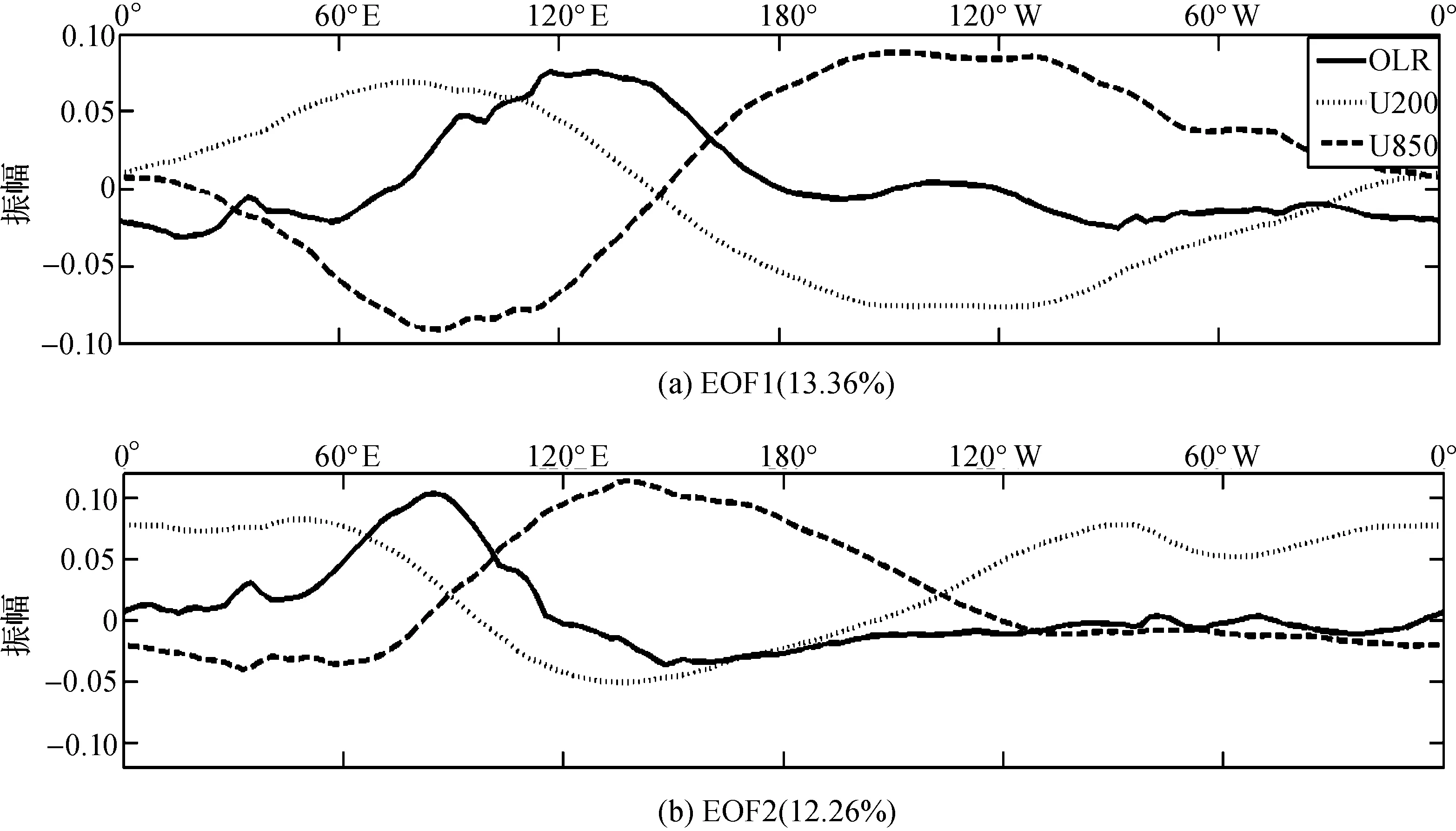
图1　利用观测OLR、U850以及U200进行联合EOF所得到的MJO的空间分布Fig.1　The spatial distribution of MJO calculated by combined EOF using observed OLR, U850 and U200

WHEELER和HENDON[64]在提出如何计算RMM的同时，也利用这个指数对MJO信号的强弱以及位相进行区分。将RMM<1的情况定义为弱MJO现象，RMM>1为强MJO现象，同时强MJO又可以根据PC1和PC2的大小关系分为8个位相。我们利用这种方法将MJO信号进行区分合成，可以得到在OLR以及低层风场(850 hPa)中MJO位相的空间分布，分别如图2和图3所示。MJO不同位相的变化间隔约为6 d，从不同位相可以看到MJO的传播和发展过程。在OLR的位相分布中，对流中心在向东发展的过程中强度不断减弱。位相1至位相4，位于太平洋的对流减弱，非洲和印度洋的对流开始建立(图2)。低层风场中，从位相4开始MJO在印度洋地区逐渐发展并伴随着向东传播的西风异常，与太平洋地区逐渐减弱的东风异常造成太平洋低层风场辐合。此外，非洲地区建立起东风异常，并与已经向东发展到海洋大陆的西风异常组成了低层风场的辐散。

图2　利用WH04方法对MJO位相进行区分得到OLR异常不同位相的空间分布Fig.2　The spatial distribution of different MJO phases in OLR anomaly, the phases were distinguished by WH04 method

图3　利用WH04方法对MJO位相进行区分得到低层风场异常(850 hPa)不同位相的空间分布Fig.3　The spatial distribution of different MJO phases in low-level wind anomaly(850 hPa), the phaseswere distinguished by WH04 method

3MJO的预报率

3.1MJO的实际预报技巧

为了客观地评价2个模式对MJO的预报技巧，我们计算了模式预报值与观测值之间的COR与RMSE。由图4a可见，CM3和CM4有相似的实际预报技巧，在初始阶段CM4的技巧略高。如果以COR为0.5作为有效预报技巧，可以发现CM3和CM4在7~10 d左右COR下降到0.5以下。在预报时效不超过10 d的条件下，2个模式对MJO都具有较好的预报能力。图4b显示2个模式的RMSE的变化非常相似，随着预报时效的增长，RMSE逐渐增加，在20 d左右预报与实际观测误差达到最大，并且稳定下来。

图4　CM3和CM4的实际预报技巧Fig.4　The actual forecast skill of models CM3 and CM4图a中水平虚线代表COR为0.5的有效预报技巧The horizontal dash line represents the least useful correlation of 0.5 in fig.a

在不考虑初始条件MJO信号强弱的前提下，CM3和CM4对RMM的有效预报技巧可以达到10 d左右。利用WHEELER和 HENDOU[64]对MJO位相进行区分的方法对初始条件MJO信号的强弱以及8个位相进行区分，可以得到表1的分布。由于强MJO信号的每个位相样本数较少，所以选取弱 MJO和强 MJO两类事件，考察初始条件MJO信号强弱对实际预报技巧的影响，并进行比较。

表1　MJO事件按位相分布的样本数

图5a和5b分别给出了CM3和CM4针对弱MJO和强MJO作为初始条件模式预报的RMM与对应观测值之间的COR，图中的误差区间为自举检验的显著性区间，自举检验设计将在3.3节中详细介绍。2个模式对弱MJO与强MJO分别作为初始条件的预报技巧差别显著，弱MJO作为初始条件时模式预报技巧明显低于强MJO。弱MJO作为初始条件时，预报时间超过7 d后，CM3的COR略有提高，但是此时CM3对RMM的实际预报技巧的有效性是值得怀疑的。以上结果表明，初始条件MJO信号的强弱对模式的预报技巧有较强的影响，在短期预报中，模式对弱MJO作为初始条件的预报技巧较差。模式的实际预报技巧受初始条件的影响显著。

3.2模式对RMM的潜在可预报率

图6显示的是模式中MJO的潜在可预报技巧，CM3和CM4在预报时效为10 d时，ACp与ACMI均可以达到0.9以上，在预报时效为25 d时仍然可以达到0.5，这说明模式对于RMM的预报技巧还有很大的提升空间。通过模式的进一步发展，可以显著提高对RMM的预报技巧，实际预报技巧可以从现在的10 d左右提升到30 d以上。

尽管ACp与ACMI两个指数在短时间内的区别并不是很明显，但是由图6可见，30 d后ACp与ACMI的差别可以达到0.1左右。这是由于ACp忽略了集合平均预报与集合成员的非线性统计关系，因此ACMI更接近真实的潜在可预报率，因此下面对潜在可预报率的讨论主要参考ACMI。

在上文对于实际预报技巧的分析中，我们发现初始条件MJO信号的强弱对实际预报技巧的影响较大。那么，潜在可预报技巧是否存在同样的规律？图7给出了利用CM3、CM4分别计算弱MJO、强MJO作为初始条件的ACMI。可以看出，在预报时效较短的情况下，强MJO为初始条件的ACMI稍高一些，但差别并不明显。初始条件MJO信号的强弱对潜在预报率的影响较小。这可能是由于初始条件的差异对模式不完美性的影响较小导致的。

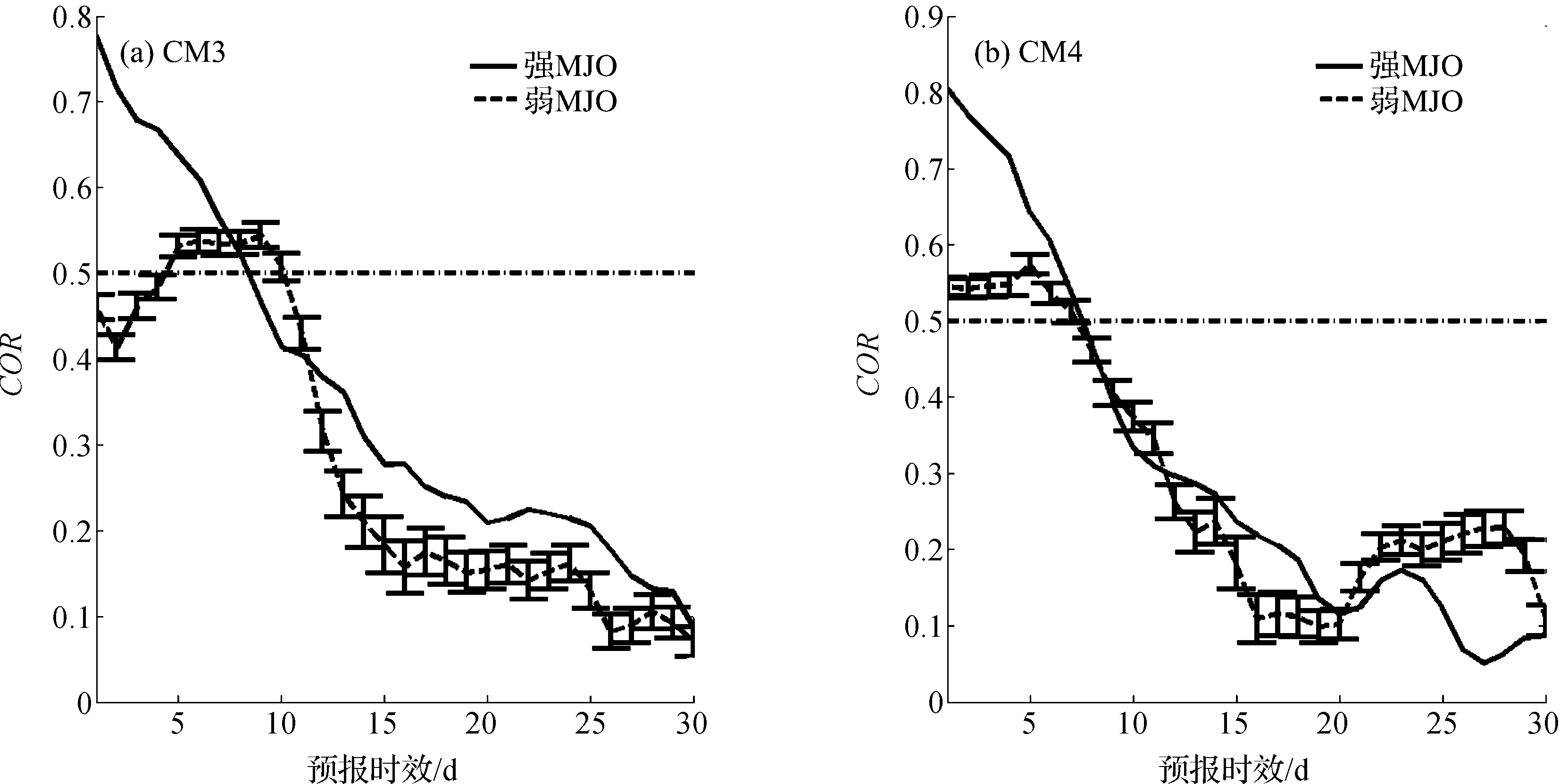
图5　弱MJO和强MJO分别作为初始条件的RMM预报值与观测值之间的CORFig.5　The correlation of observed RMM and predicted RMM with weak MJO and strong MJO as the initial condition respectively水平虚线代表COR为0.5的有效预报技巧；误差区间为自举检验的显著性区间The horizontal dash line represent the least useful correlation of 0.5, vertical error bars represent the sample standard deviation calculated using bootstrap experiment

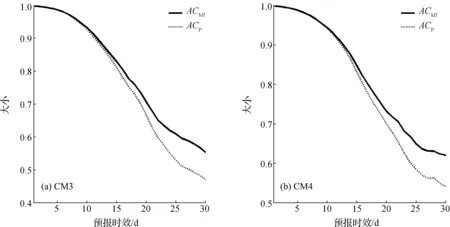
图6　预报数据中RMM的潜在可预报率Fig.6　The potential predictability of RMM in the forecast data

图7　弱MJO和强MJO分别作为初始条件下预报数据的ACMI指标Fig.7　The ACMI of forecast data with weak MJO and strong MJO as the initial condition respectively误差区间为自举检验的显著性区间；由于指标的自举检验置信区间较小，在图中变现为1条直线Vertical error bars represent the sample standard deviation calculated using bootstrap experiment.The standard deviation of ACMI is small, expressed as a straight line in the figure

在计算ACp过程中可以得到预报数据中信号和噪音的分布，在一定程度上信号与噪音的变化决定了模式对RMM的潜在预报率。如图8所示，在CM4中随着预报时间的增加，信号成分逐渐减少，噪声逐渐加强，噪声在20 d 左右超过信号，对比图4中COR的变化趋势可以发现CM4对RMM的实际预报技巧大约在20 d左右降到最低，同时RMSE的变化也在20 d左右达到最大。因此，提高模式中信号的分布或者降低噪声的分布都会明显提升模式的实际预报技巧，因此在下一节将通过使用时间平均来降低噪声的分布，从而提升模式的预报能力。

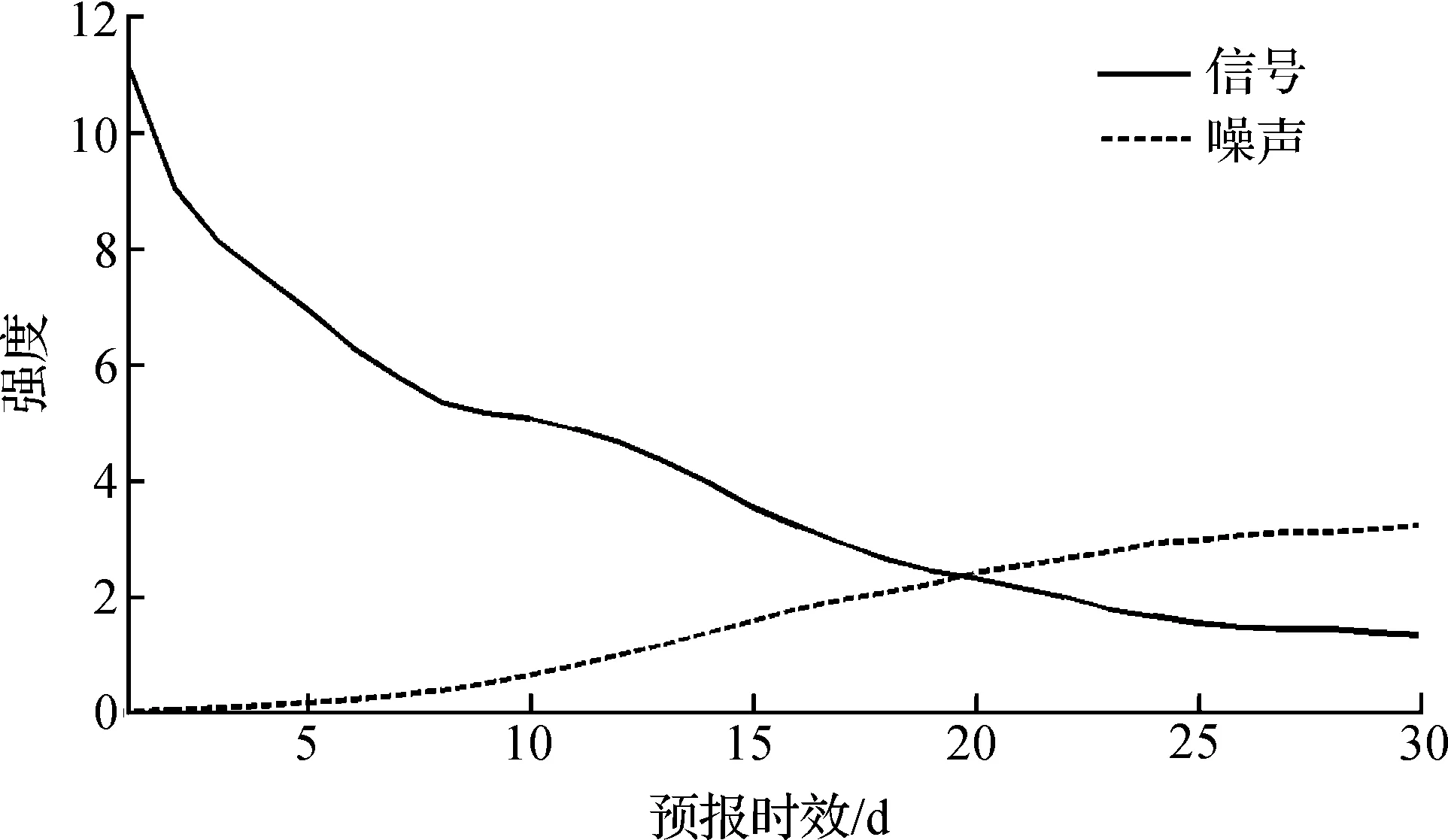
图8　CM4中信号和噪声的变化Fig.8　The variety of signal and noise in model CM4

3.3不同时间尺度平均对RMM预报技巧的影响

在前文的计算结果中，对于实际预报技巧及潜在预报率的考察都是基于日平均的时间尺度。在本节中，将计算不同时间尺度平均下模式对RMM的实际预报技巧和潜在预报率。由于t检验需要有效自由度，而对于时间平均很难估计样本的有效自由度，因此利用自举检验代替t检验得到不同时间平均下的置信区间。自举检验的设计方法如下：(1)将1979—2010年的观测与预报数据，根据不同的时间尺度，组成一对；(2)在所有的观测-预报组合中随机选取95%的成员分别计算COR和RMSE；(3)重复上一步骤1 000次得到的标准差作为给定置信度的置信区间[65]。在检验潜在可预报率时，只需要在步骤1中将预报数据按照不同时间尺度进行计算，然后重复步骤2、3。

图9分别给出了CM3和CM4在不同时间尺度平均下COR以及RMSE的计算结果，并与日平均数据计算得到的结果进行对比，图中的误差区间为自举检验的显著性区间，时间平均分别选取5 d和10 d进行计算。从图9a和图9b可以看出，5 d和10 d平均比日平均的COR有一定的提高，但是并不明显。图9c和图9d为RMSE在不同时间尺度平均下的计算结果，不论是5 d还是10 d平均的RMSE都比日平均小很多，并且这种差异比较显著。由此可见，通过不同时间尺度的平均可以明显减弱RMSE增强的幅度，提升模式的预报技巧。

图9　CM3和CM4中不同时间平均尺度的实际预报技巧Fig.9　The actual forecast skill over different averaging time scales in models CM3 and CM4图中的误差区间为自举检验的显著区间Vertical error bars represent the sample standard deviation calculated using bootstrap experiment

为进一步考察时间平均的影响，计算了10 d平均与日平均预报技巧的相对差别。对10 d的资料平均所得到的技巧为R10，这个相对差别被定义为：

(17)

(18)

其中：R1是原始日平均数据,i是原始数据时间。该差别反映了时间平均后的预报技巧相对于日平均的预报技巧的提高。图10是CM4的10 d平均与日平均的相对差别BB。在图9中COR的变化并不明显，但是通过图10可以发现COR的相对变化可以达到0.1以上，时间平均对COR的影响比较明显。由此可见，时间平均可以有效地滤除预报数据中低频的噪声，从而提高信号的比例。

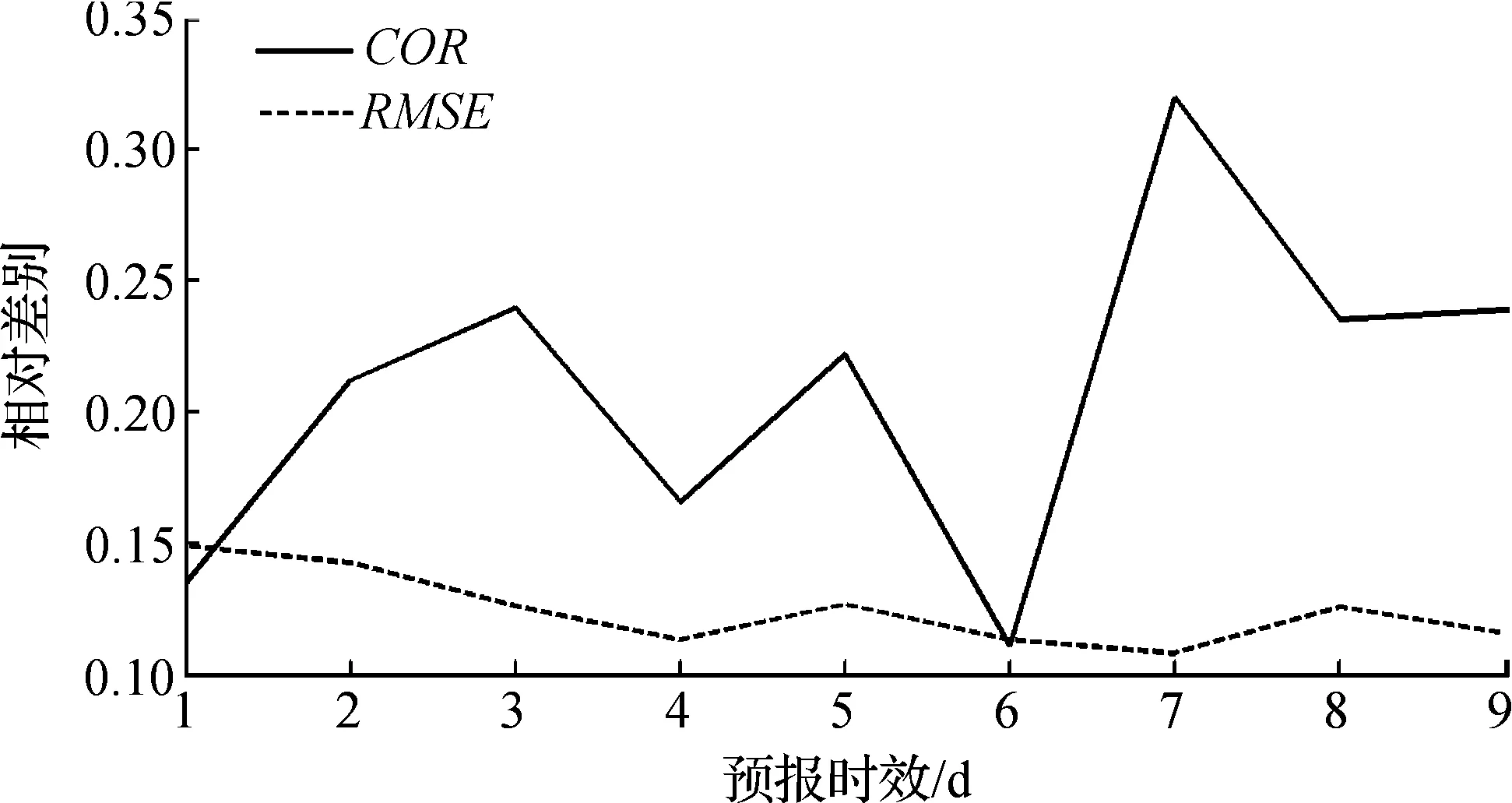
图10　CM4中10 d平均下的COR和RMSE相对于日平均数据的相对变化Fig.10　The relative change of COR and RMSE between tendays mean and daily mean in model CM4

为考察潜在预报率是否也受到时间尺度变化的影响，我们作了类似分析。图11分别计算了CM3和CM4中ACMI在不同时间尺度平均下的变化。图中ACMI随着时间尺度的增加相应提高，而且ACMI的检验误差很小，趋近于0,表明时间平均对ACMI的提高比较显著。与日平均的潜在可预报技巧相比，随着时间平均的增加，潜在预报率也相应提高。影响大气可预报性的主要误差来源于非线性的噪声和模式的随机误差。通过时间平均可以降低非线性噪声和随机误差对MJO低频信号的干扰，从而提高MJO的可预报技巧。

3.4ISV最可预报的空间型

虽然利用RMM可以简单直观地发现潜在预报率的特征，但是一维的指数很难描述复杂的大气环流结构，因此本节将利用PrCA方法分析模式中ISV最可预报模态的空间分布。

第2节中，在纬向平均的基础上得到了MJO空间模态，利用这种方法计算得到的RMM与WH04的相关较好，因此在保证观测数据处理合理的前提下，本文利用未进行纬向平均的观测数据进行联合EOF得到MJO二维空间模态。与之对应的PC1和PC2与WH04的相关系数可以达到0.79和0.80,说明未进行纬向平均的数据同样可以维持较强的MJO信号。由此得到的MJO二维空间模态如图12所示，通过这种二维分布，能够更加明显地看出MJO的水平空间结构，同时有助于与PrCA得到的结果进行对比。

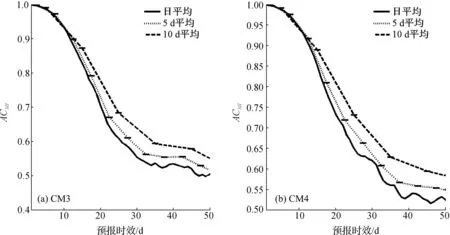
图11　不同时间尺度平均下的预报数据ACMI指标Fig.11　The ACMIover different averaging time scale图中的误差区间为自举检验的显著区间Vertical error bars represent the sample standard deviation calculated using bootstrap experiment

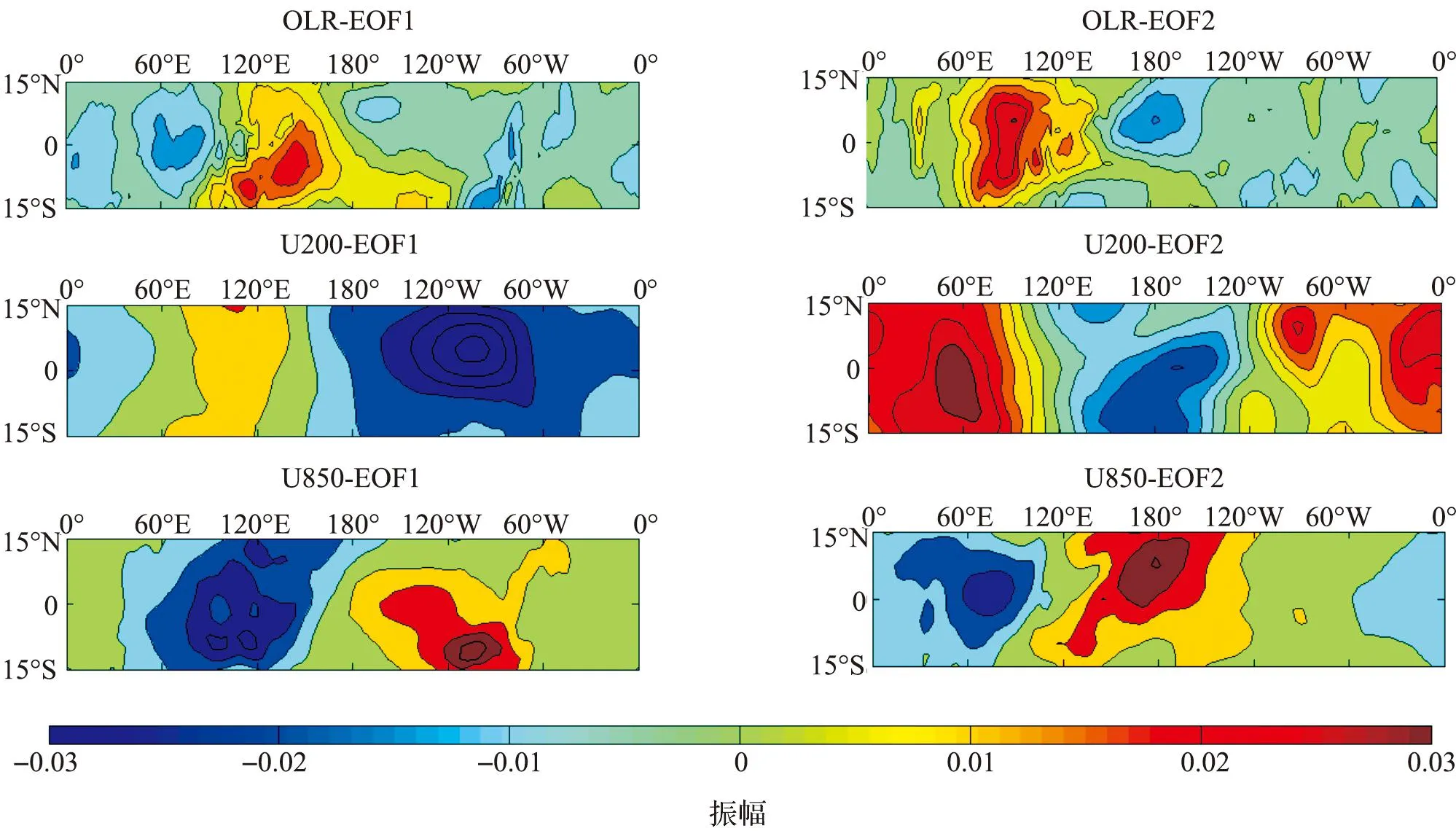
图12　利用未进行纬向平均的观测数据进行EOF得到的MJO空间模态Fig.12　The spatial distribution of MJO calculated by EOF using observed data without meridional mean

PrCA主要是发现最可预报成分及相应的最可预报的空间模态。对CM3和CM4中OLR、U200和U850三个变量的联合场进行PrCA分析，得到的ISV最可预报的空间分布分别如图13和图14所示，通过对比PrCA的结果与观测MJO的EOF空间模态(图12)可以发现，PrCA的第1空间模态(PrCA1)与EOF2相似，并且PrCA的第2空间模态(PrCA2)与EOF1非常相似。PrCA的2个模态中纬向风场存在斜压结构，同时表现出MJO纬向1波的特征，这表明MJO是ISV最可预测的空间结构。由于PCA是利用解释方差得到不同的空间模态，而PrCA是考察潜在预报率最大的模态，因此导致了PrCA的计算结果与PCA结果的区别。

图13　CM3预报数据进行PrCA计算得到的最可预报的2个空间模态Fig.13　Two of the most predictable components in model CM3 calculated by PrCA

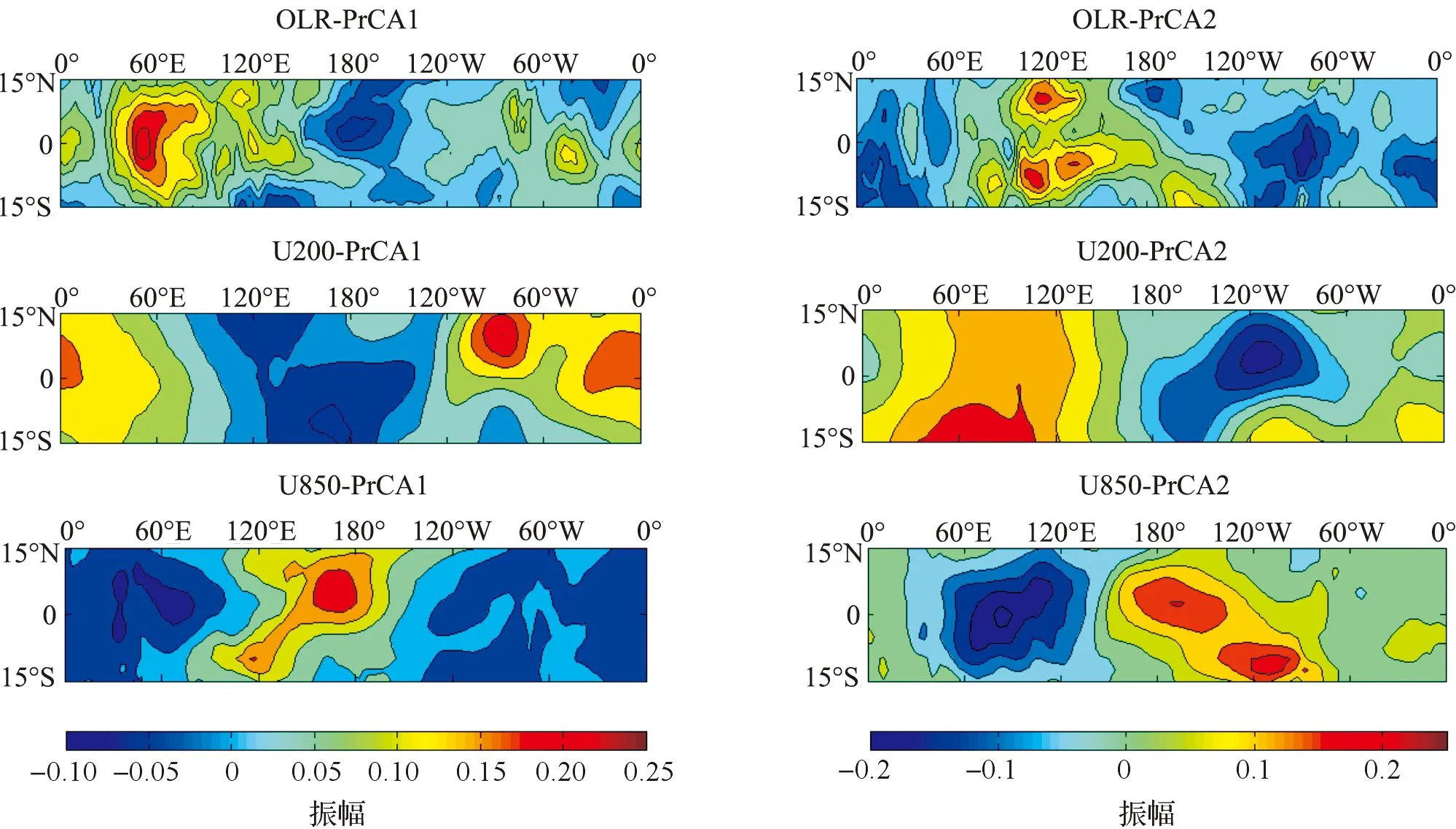
图14　CM4预报数据进行PrCA计算得到的最可预报的2个空间模态Fig.14　Two of the most predictable components in model CM4 calculated by PrCA

为了进一步探讨PrCA在预报中的应用，将观测OLR、U200和U850变量的联合场投影到PrCA的空间模态上，得到1组新的时间序列，计算2组时间序列的COR可以得到图15的结果。如果同样以相关系数0.5作为有效预报技巧，可以发现PrCA刻画的时间序列与观测有很好的相关关系，预报时效可以达到20 d左右。对比上文10 d左右的预报时效，PrCA能显著地提高预报技巧。因此，在进行ISV业务化预报时，也许可以选择PrCA作为预报对象，从而得到更高的预报技巧。

图15　将CM3和CM4观测数据变量场投影到PrCA空间结构上得到的时间序列与PrCA序列的CORFig.15　Correlation between the observation projected time series and PrCA time series for models CM3 and CM4

4结论

MJO作为热带大气重要的季节内变化，已经受到国内外学者的广泛关注，MJO的数值模拟以及预报已经成为大气科学的前沿问题。本文利用集合预报产品和以信息论为基础的可预报性框架，研究了MJO的实际预报技巧和潜在预报率。

通过计算发现，所选择的2个加拿大模式CM3和CM4对MJO有相似的预报技巧，预报时效约为10 d。模式对RMM的实际预报技巧受初始条件MJO信号的强弱影响较大，在初始条件为弱MJO信号的情况下，模式对MJO的预报效果相对较差。另一方面，相比于实际预报技巧，潜在可预报技巧受初始条件影响较小。CM3和CM4对MJO的潜在可预报技巧可以达到30 d以上，模式有较大改进空间。值得注意的是，在潜在预报率的计算中，ACMI比ACp更能准确地反映模式真实的潜在预报率。RMM的潜在可预报技巧在不同时间尺度下变化显著，通过时间平均可以有效降低预报与观测的绝对差异，降低模式中的非线性和随机噪声对预报的影响，从而提高潜在可预报技巧。

通过PrCA的计算可以发现，模式中MJO是ISV最可预报的空间分布，其中最可能得到的预报空间分布为MJO的第2空间模态，因此在热带大气的低频振荡中潜在预报率最高的信号是MJO。另外，利用PrCA得到的时间序列还可以为预报ISV提供一种新的方法。将PrCA方法应用于RMM的预报还需要更多的探索。

参考文献(References)：

[1] MADDEN R A, JULIAN P R. Detection of a 40-50 day oscillation in the zonal wind in the tropical Pacific[J]. Journal of the Atmospheric Sciences,1971,28(5):702-708.

[2] ZHANG Guang-jun，MU Ming-quan. Simulation of the Madden-Julian Oscillation in the NCAR CCM3 using a revised Zhang-McFarlane convection parameterization scheme[J]. Journal of Climate,2005,18(19):4 046-4 064.

[3] ZHOU Lei, MURTUGUDDE R. Influences of Madden-Julian Oscillations on the eastern Indian Ocean and the maritime continent[J]. Dynamics of Atmospheres and Oceans,2010,50(2):257-274.

[4] CHEN Guang-hua, Huang Rong-hui. Dynamical effects of low frequency oscillation on tropical cyclogenesis over western North Pacific and the physical mechanisms[J].Chinese J Atmos Sci: in Chinese，2009，33(2):205-214.

陈光华,黄荣辉.西北太平洋低频振荡对热带气旋生成的动力作用及其物理机制[J].大气科学，2009,33(2)：205-214.

[5] SUN Zhang, MAO Jiang-yu, WU Guo-xiong. Influences of intraseasonal oscillationson the clustering of tropical cyclone activities over the western North Pacific during boreal summer[J]. Chinese J Atmos Sci: in Chinese，2009，33(5):950-958.

孙长,毛江玉,吴国雄.大气季节内振荡对夏季西北太平洋热带气旋群发性的影响[J].大气科学，2009，33(5):950-958.

[6] PAN Jing, LI Chong-yin, SONG Jie. The modulation of Madden-Julian oscillation on typhoons in the Northwestern Pacific Ocean[J]. Chinese J Atmos Sci: in Chinese,2010,34(6):1 059-1 070.

潘静,李崇银,宋洁.热带大气季节内振荡对西北太平洋台风的调制作用[J].大气科学,2010，34(6):1 059-1 070.

[7] TIAN Hua, LI Chong-yin, YANG Hui. Modulation of typhoon genesis over the western North Pacific by intraseasonal oscillation[J].Journal of Tropical Meteorology:in Chinese,2010,26(3):283-292.

田华,李崇银,杨辉.热带大气季节内振荡对西北太平洋台风生成数的影响研究[J].热带气象学报，2010，26(3)：283-292.

[8] WEBSTER P J, MAGANA V O, PALMER T N, et al. Monsoons: Processes, predictability, and the prospects for prediction[J]. Journal of Geophysical Research: Oceans (1978-2012),1998,103(C7):14 451-14 510.

[9] LIN Ai-lan, LIANG Jian-yin, LI Chun-hui. Spectral variation characteristics of South China Sea summer monsoon convection in intraseasonal oscillation[J].Journal of Tropical Meteorology: in Chinese,2005,21(5):542-548.

林爱兰,梁建茵,李春晖.南海夏季风对流季节内振荡的频谱变化特征[J].热带气象学报，2005，21(5):542-548.

[10] JIA Xiao-long, LIANG Yun. Possible impacts of the MJO on the sever ice snow weather in November of 2009 in China [J]. Journal of Tropical Meteorology: in Chinese,2011,27(5):639-648.

贾小龙,梁云.热带MJO对2009年11月我国东部大范围雨雪天气的可能影响[J].热带气象学报，2011，27(5)：639-648.

[11] BAI Xu-xu, LI Chong-yin, TAN Yan-ke, et al. The impacts of the MJO (Madden-Julian Oscillation)on spring rainfall in East China [J].J Trop Meteor: in Chinese,2011,27(6):814-822.

白旭旭,李崇银,谭言科,等.MJO对我国东部春季降水影响的分析[J].热带气象学报，2011,27(6)：814-822.

[12] DING Yi-hui, LI Chong-yin. Onset and evolution of the South China Sea monsoon and its interaction with the Ocean[M]. Beijing: China Meteorological Press,1999.

丁一汇，李崇银.南海夏季风爆发和演变及其与海洋相互作用[M].北京：气象出版社,1999.

[14] KESSLER W S, KLEEMAN R. Rectification of the Madden-Julian Oscillation into the ENSO cycle[J]. Journal of Climate,2000,13(20):3 560-3 575.

[15] TANG You-min, YU Bing. MJO and its relationship to ENSO[J]. Journal of Geophysical Research: Atmospheres(1984-2012),2008,113(D14):762-770.

[16] CASSOU C. Intraseasonal interaction between the Madden-Julian oscillation and the North Atlantic oscillation[J]. Nature,2008,455(7212):523-527.

[17] ZHANG C, GOTTSCHALCK J, MALONEY E D, et al. Cracking the MJO nut[J]. Geophysical Research Letters,2013,40(6):1 223-1 230.

[18] CHOU Ji-fan, ZHENG Zhi-hai, SUN Shu-peng. Numerical prediction of 10-30 dextension period-chaos[J].Chinese J Atmos Sci: in Chinese,2010,30(5):569-573.

丑纪范，郑志海，孙树鹏，10-30d延伸期数值天气预报的策略思考——直面混沌[J].气象科学，2010，30(5)：569-573.

[19] LIANG Ping, DING Yi-hui. Extended forecast test based on intraseansonal oscillation[J]. Chinese J Atmos Sci: in Chinese,2012,36(1):102-116.

梁萍，丁一汇.基于季节内振荡的延伸预报试验[J].大气科学，2012，36(1)：102-116.

[20] LAU W K M, WALISER D E. Intraseasonal variability in the atmosphere-ocean climate system[M]. Springer Science & Business Media,2011.

[21] SEO K H, WANG W, GOTTSCHALCK J, et al. Evaluation of MJO forecast skill from several statistical and dynamical forecast models[J]. Journal of Climate,2009,22(9):2 372-2 388.

[22] KANG I S, KIM H M. Assessment of MJO predictability for boreal winter with various statistical and dynamical models[J]. Journal of Climate,2010,23(9):2 368-2 378.

[23] SLINGO J M, SPERBER K R, BOYLE J S, et al. Intraseasonal oscillations in 15 atmospheric general circulation models: Results from an AMIP diagnostic subproject[J]. Climate Dynamics,1996,12(5):325-357.

[24] LIN H, BRUNET G, DEROME J. Forecast skill of the Madden-Julian Oscillation in two Canadian atmospheric models[J]. Monthly Weather Review,2008,136(11):4 130-4 149.

[25] KIM H M, WEBSTER P J, CURRY J A. Impact of shifting patterns of Pacific Ocean warming on North Atlantic tropical cyclones[J]. Science,2009,325(5936):77-80.

[26] LIU Ping, WANG Bin, SPERBER K R, et al. MJO in the NCAR CAM2 with the Tiedtke Convective Scheme*[J]. Journal of Climate,2005,18(15):3 007-3 020.

[27] JIA Xiao-long, LI Chong-yin. Sensitivity of simulated tropical intraseasonal oscillation to cumulus parameterizations [J]. Acta Meteor Sin: in Chinese,2007,65(6):837-854.

贾小龙,李崇银.热带大气季节内振荡数值模拟对积云对流参数化方案的敏感性[J].气象学报，2007，65(6)：837-854.

[28] VITART F, HUDDLESTON M R, DÉQUÉ M, et al. Dynamically-based seasonal forecasts of Atlantic tropical storm activity issued in June by EUROSIP[J].Geophysical Research Letters,2007,34(16):130-144.

[29] INNESS P M, SLINGO J M, WOOLNOUGH S J, et al. Organization of tropical convection in a GCM with varying vertical resolution; implications for the simulation of the Madden-Julian Oscillation[J]. Climate Dynamics,2001,17(10):777-793.

[30] JIA Xiao-long, LI Chong-yin, LING Jian. Impacts of cumulus parameterization and resolutions on the MJO simulation[J].Journal of Tropical Meteorology: in Chinese,2009,25(1):1-12.

贾小龙,李崇银,凌健.积云参数化和分辨率对MJO数值模拟的影响[J].热带气象学报，2009，25(1)：1-12.

[31] HENDON H H, LIEBMANN B, NEWMAN M, et al. Medium-range forecast errors associated with active episodes of the Madden-Julian Oscillation[J]. Monthly Weather Review,2000,128(1):69-86.

[32] FU Xiou-hua, WANG Bin, WALISER D E, et al. Impact of atmosphere-ocean coupling on the predictability of Monsoon Intraseasonal Oscillations[J]. Journal of the Atmospheric Sciences,2007,64(1):157-174.

[33] FU Qiang, MANABE S, JOHANSON C M. On the warming in the tropical upper troposphere: Models versus observations[J]. Geophysical Research Letters,2011,38(15):532-560.

[34] WALISER D E, LAU K M, STERN W, et al. Potential predictability of the Madden-Julian oscillation[J]. Bulletin of the American Meteorological Society,2003,84(1):33-50.

[35] PEGION K, KIRTMAN B P. The impact of air-sea interactions on the simulation of tropical intraseasonal variability[J]. Journal of Climate,2008,21(24):6 616-6 635.

[36] NEENA J M, LEE J Y, WALISER D, et al. Predictability of the Madden-Julian Oscillation in the Intraseasonal Variability Hindcast Experiment (ISVHE)*[J]. Journal of Climate,2014,27(12):4 531-4 543.

[37] TANG You-min, CHEN Da-ke, YANG De-jian, et al. Methods of estimating uncertainty of climate prediction and climate change projection[M]//SINGH B R. Climate change-realities, impacts over ice cap, sea level and risks. Croatia InTeeh,2013:397-420.

[38] LAPRISE R, GIRARD C. A spectral general circulation model using a piecewise-constant finite-element representation on a hybrid vertical coordinate system[J]. Journal of Climate,1990,3(1):32-52.

[39] VERSEGHY D L. CLASS—A Canadian land surface scheme for GCMs. I. Soil model[J]. International Journal of Climatology,1991,11(2):111-133.

[40] ABDELLA K, MCFARLANE N A. Parameterization of the surface-layer exchange coefficients for atmospheric models[J]. Boundary-Layer Meteorology,1996,80(3):223-248.

[41] ZHANG Guang-jun, MCFARLANE N A. Sensitivity of climate simulations to the parameterization of cumulus convection in the Canadian Climate Centre general circulation model[J]. Atmosphere-Ocean,1995,33(3):407-446.

[42] LI Jiang-nan. Accounting for unresolved clouds in a 1D infrared radiative transfer model. Part I: Solution for radiative transfer, including cloud scattering and overlap[J]. Journal of the Atmospheric Sciences,2002,59(23):3 302-3 320.

[43] LI Jiang-nan, BARKER H W. Accounting for unresolved clouds in a 1D infrared radiative transfer model. Part II: Horizontal variability of cloud water path[J]. Journal of the Atmospheric Sciences,2002,59(23):3 321-3 339.

[44] LI Jiang-nan, BARKER H W. A radiation algorithm with correlated-k distribution. Part I: Local thermal equilibrium[J]. Journal of the Atmospheric Sciences,2005,62(2):286-309.

[45] PINCUS R, BARKER H W, MORCRETTE J J. A fast, flexible, approximate technique for computing radiative transfer in inhomogeneous cloud fields[J]. Journal of Geophysical Research: Atmospheres (1984-2012),2003,108(D13):909-924.

[46] LOHMANN U, FEICHTER J, CHUANG C C, et al. Prediction of the number of cloud droplets in the ECHAM GCM[J]. Journal of Geophysical Research: Atmospheres (1984-2012),1999,104(D8):9 169-9 198.

[47] VON SALZEN K, LEIGHTON H G, ARIYA P A, et al. Sensitivity of sulphate aerosol size distributions and CCN concentrations over North America to SOx emissions and H2O2 concentrations[J]. Journal of Geophysical Research,2000,105(D8):9 741-9 765.

[48] LOHMANN U, ROECKNER E. Design and performance of a new cloud microphysics scheme developed for the ECHAM general circulation model[J]. Climate Dynamics,1996,12(8):557-572.

[49] GENT P R, BRYAN F O, DANABASOGLU G, et al. The NCAR climate system model global ocean component*[J]. Journal of Climate,1998,11(6):1 287-1 306.

[50] LARGE W G, MCWILLIAMS J C, DONEY S C. Oceanic vertical mixing: A review and a model with a nonlocal boundary layer parameterization[J]. Reviews of Geophysics,1994,32(4):363-403.

[51] SIMMONS H L, JAYNE S R, LAURENT L C S, et al. Tidally driven mixing in a numerical model of the ocean general circulation[J]. Ocean Modelling,2004,6(3):245-263.

[52] LARGE W G, DANABASOGLU G, MCWILLIAMS J C, et al. Equatorial circulation of a global ocean climate model with anisotropic horizontal viscosity[J]. Journal of Physical Oceanography,2001,31(2):518-536.

[53] KUMAR A, HOERLING M P. Annual cycle of Pacific-North American seasonal predictability associated with different phases of ENSO[J]. Journal of Climate,1998,11(12):3 295-3 308.

[54] SHUKLA J. Predictability in the midst of chaos: A scientific basis for climate forecasting[J]. Science,1998,282(5389):728-731.

[55] PENG Ping, KUMAR A, WANG Wen-shou. An analysis of seasonal predictability in coupled model forecasts[J]. Climate Dynamics,2011,36(3-4):637-648.

[56] TANG You-min, LIN Hai, MOORE A M. Measuring the potential predictability of ensemble climate predictions[J]. Journal of Geophysical Research: Atmospheres(1984-2012),2008,113(D4):84-84.

[57] DELSOLE T, TIPPETT M K. Predictability: Recent insights from information theory[J]. Reviews of Geophysics,2007,45(4):429-430.

[58] YANG De-jian,TANG You-min,ZHANG Yao-cun, et al. Information-based potential predictability of the Asian summer monsoon in a coupled model[J]. Journal of Geophysical Research: Atmospheres(1984-2012),2012,117(D3):812-819.

[59] VENZKE S, ALLEN M R, SUTTON R T, et al. The atmospheric response over the North Atlantic to decadal changes in sea surface temperature[J]. Journal of Climate,1999,12(8):2 562-2 584.

[60] SCHNEIDER T, GRIFFIES S M. A conceptual framework for predictability studies[J]. Journal of Climate,1999,12(10):3 133-3 155.

[61] ALLEN M R, SMITH L A. Optimal filtering in singular spectrum analysis[J]. Physics Letters A,1997,234(6):419-428.

[62] SUTTON R T, JEWSON S P, ROWELL D P. The elements of climate variability in the tropical Atlantic region[J]. Journal of Climate,2000,13(18):3 261-3 284.

[63] TANG You-min, KLEEMAN R, MOORE A M. Comparison of information-based measures of forecast uncertainty in ensemble ENSO prediction[J]. Journal of Climate,2008,21(2):230-247.

[64] WHEELER M C, HENDOU H H. An all-season real-time multivariate MJO index: Development of an index for monitoring and prediction[J]. Monthly Weather Review,2004,132(8):1 917-1 932.

[65] YOUNAS W, TANG You-min. PNA predictability at various time scales[J]. Journal of Climate,2013,26(22):9 090-9 114.

刘成璟，章向明，唐佑民.东亚夏季风降雨的可预报性研究[J].海洋学研究,2015,33(4):17-29,doi:10.3969/j.issn.1001-909X.2015.04.002.

LIU Cheng-jing，ZHANG Xiang-ming，TANG You-min. Predictability of the East-Asian summer monsoon rainfall in two coupled models[J]. Journal of Marine Sciences, 2015, 33(4):17-29, doi:10.3969/j.issn.1001-909X.2015.04.002.

Forecast skill of MJO in two coupled models

LIU Da1,2, ZHANG Xiang-ming*1,2，TANG You-min1,2,3

(1.StateKeyLaboratoryofSatelliteOceanEnvironmentDynamics,Hangzhou310012,China; 2.TheSecond

InstituteofOceanography,SOA,Hangzhou310012,China; 3.EnvironmentScienceandEngineering,

UniversityofNorthernBritishColumbia,PrinceGeorgeV2N4Z9,Canada)

Abstract:Using the production of two coupled model from CCCma, and based on the information theory,the predictability of the Madden-Julian Oscillation including the actual forecast skill and potential predictability and the most predictable compnents of ISV were evaluated.The influence of different average time scale was also discussed. It is found that MJO has skillful forecast up to the lead time around ten days in these two coupled models, similar to the current forecast models.MJO can be forecasted potentially at more than one month of lead time. The actual forecast skill and potential predictability of MJO can be further developed as the averaging time scale increased from daily to ten days， especially the potential predictability increased more significantly. Further analysis found that the MJO signal strength of initial condition is the main factor to influence the forecast skill, if the MJO signal is strong, it has the best skill, vice versa. At last,the most predictable distributions of ISV were analyzed and the methods using such distributions to improve the actual forecast skill of ISV were discussed.

Key words:MJO；forecast skill；potential predictability；the most predictable component

通讯作者：*章向明(1959-)，男，工程师，主要从事海-气相互作用方面的研究。E-mail:zhangxm@sio.org.cn

作者简介:刘成璟(1990-)，男，江苏盐城市人，主要从事可预报性方面的研究。E-mail:crucios@163.com

基金项目:国家自然科学基金项目资助(41276029)

收稿日期:2015-04-22修回日期:2015-06-09

Doi:10.3969/j.issn.1001-909X.2015.04.001

中图分类号:P456.7

文献标识码:A

文章编号:1001-909X(2015)04-0001-16