基于遗传算法的电动汽车充电站布局的最优规划

刘　飞

(北京物资学院，北京101149)

基于遗传算法的电动汽车充电站布局的最优规划

刘飞

(北京物资学院，北京101149)

摘要：电动汽车充电站是电动汽车市场化、产业化的重要支撑系统，对电动汽车充电站的布局规划进行研究，构建完善的充电服务网络，有利于电动汽车的推广。首先分析了电动汽车充电站布局规划相关研究现状，总结了目前充电站布局规划存在的问题，根据区域交通流量守恒原理对所要规划的区域进行充电需求小区的划分，并对其划分原则和可行性进行了探讨。然后利用单目标非线性规划建立了充电站投资成本、运行及维护成本的最小化的布局规划模型。在模型的优化求解方面，传统的优化算法很难求解这样复杂的问题，选择了遗传算法求得模型的最优解，确定了充电站的位置和容量，并用实例得出了优化后的充电站及其服务范围，验证了模型的准确性和有效性，为充电站布局规划工作提供了一定的经验。

关键词：电动汽车充电站；布局规划；遗传算法；服务网络成本最小

中图分类号：TM715

文献标识码:A

DOI:10.3969/j.issn.1672-0792.2015.08.007

收稿日期：2015-05-28。

作者简介：刘飞(1991-),男，硕士研究生，研究方向为物流系统规划，E-mail:liuxinye121@126.com。

Abstract：Electric vehicle charging stations are important support system for electric vehicle marketization and industrialization. To study the electric vehicle charging stations’ layout planning and building a sound network of services are in favor of the promotion of electric vehicles. This paper first analyzes the layout planning related research status of electric vehicle charging stations, summarizes the current problems of the charging station layout planning, according to the regional traffic flow conservation principle to divide the area into charging requirements cell, and its principles and feasible division nature were discussed. Then use the single nonlinear objective programming to establish a layout planning model whose charging stations investment costs, operation and maintenance costs are minimum. In terms of the model optimal solution, the traditional optimization algorithm is difficult to solve such a complex problem, the article choose to use the genetic algorithm to obtain the optimal solution of the model, in order to determine the location and capacity of the charging station, and the use of the example verify the accuracy and validity of the model. Finally, this article obtains charging stations and services which are optimized with examples, to verify the accuracy and validity of the model, and provide some experience for the charging station layout planning.

Keywords：electric vehicle charging station; layout; genetic algorithm; network cost minimization

0引言

汽车在城市的发展中起了不可忽视的作用，但是传统的汽车使用的能源多是油气，这样不仅大量有污染性的气体被排放到环境中，而且还使不能再生资源供应加剧紧张。《BP年世界能源统计年鉴2014》显示2013年中国已成为仅次于美国石油消费量第二的国家，天然气消费增速达到10.8%，为当年天然气消费量最大的国家[1]。其中车用油气是这些能源大幅度增长的原因之一，而且还有扩张的趋势。

就汽车行业本身来说，解决油气短缺限制发展的问题，现实的选择是从节约使用和替代两个方面入手，即发展新能源汽车[2]。作为新能源汽车之一，电动汽车使用的电能来源主要是太阳能、风力、燃料、水力，一般没有直接排放的污染物，对环境污染甚小。建设和发展电动汽车充电设施有利于电动汽车产业的推广。充电设施是电动汽车商业化、产业化过程中的重要因素，主要包括交流充电桩、充电站、电池更换站3种类型[3]。近年来，随着车用电池技术的不断突破，以及政府的大力支持，电动汽车在各国、各城市得到了广泛的推广应用[4，5]，纯电动汽车和可插电外充的混合动力电动汽车主要以集团化用车为主，已在许多国家和地区示范应用，充电基础设施也正在加紧建设中[6]。

由于电动汽车越来越多的优势被人熟知，电动汽车保有量的不断加大带来了充电需求的加大，这时候充电需求就需要量化。王飞龙等[7]根据用户的数量，考虑充电时间等因素，利用多元线性回归和Bass扩散模型对充电需求进行了预测。量化了充电需求，就要对充电站布局规划，鉴于目前落后的现状，充电站的布局规划也就成了国内外学者研究的热点。张成等[8]用网格法确定规划区充电站站址，并提出了负荷率控制系数和充电负荷密集区等概念，接着建立了充电站规划模型和充电站盈利模型。王泽黎等[9]应用混沌粒子群算法优化了充电站的布局。葛少云等[10]在充分考虑路网结构、车流信息和用户路程损耗等因素的情况下提出充电站选址定容的优化方法，并利用加权Voronoi图来实现充电站服务范围的自动划分，然后以全社会成本最小为目标从多种规划方案中选择最优的方案。孙小慧[11]从燃料需求的空间分布角度出发，解决了需求点与供应站之间的总距离最小、供应站服务的需求量最大、以及基于此两类目标的多目标优化问题。林琳等[12]分析了电动汽车的充电行为，然后建立了充电服务系统的排队模型，旨在寻求顾客与充电站服务设置之间的平衡，保证充电站最佳服务能力和最合理配置。虽然这些文献考虑到布局规划的影响因素并构建了数学模型，但是并没有充分考虑充电用户的充电需求，没有让资源得到充分利用，做到充电站服务网络总成本最小。本文首先最大化的考虑用户的充电需求，然后构建了充电站布局的最优规划模型，通过模型的优化求解，确定了充电站站址和规模。

1电动汽车充电站布局规划的数学模型

首先在选定的规划区域内划分充电需求小区，然后构建总成本最小化的目标函数，通过优化求解确定充电站的规模和位置。因为电动公交车、环卫电动汽车等集团用车具有特定的停车场所和几乎不改变的路线，所以它们的充电站的布局规划可以采取固定的模式。但是电动出租车等乘用车行驶自由，没有固定的模式，建立充电需求小区可以将问题简化，本文的研究对象设定为集中公用充电站，服务车辆为出租车和私家车。

1.1　充电需求小区的划分

充电需求小区法是把电动汽车的充电需求不规则的划分为若干个充电小区，每一个充电小区的充电需求在其几何中心，并且建立投资成本、运行及维护成本的优化函数来确定充电站的位置和容量[13]。

(1)可行性

需求小区的重心和电动汽车的数量在一定的时期内不变，这样就可以把具有充电需求的电动汽车看成是位于这个区域重心位置的负荷点。另外，在充电站的建设初期，建设单位为了统一协调供电，以便发挥供需双方最大的经济效益，会指导充电的用户到附近的充电站进行充电，这样充电用户就会固定在某处充电，使得充电需求小区更符合实际。另外根据区域交通流量守恒原理，单位时间内，某一区域内的电动汽车进出数量是一致的，区域内的电动车数量是一定的。所以某充电站需要提供的充电服务次数需求可以参照某一区域内电动汽车的数量。

(2)划分原则

充电需求小区的划分要做到科学、合理，应充分考虑各种影响因素，目前充电需求小区的划分遵循下列几点：

1)由于充电安全和征地成本较高的原因，充电站不宜设在城市中心区域，因此划分时排除中心区域；

2)充电需求小区应充分把电动汽车的续航里程考虑在内，在充电需求比较集中的地方向周围辐射，选择的区域适当小，控制在合理范围内；

3)尽量把用户少的需求点放在充电小区边缘，适当考虑城市的自然分界和街道路网结构；

4)考虑区域用地性质。

总之，充电需求小区的划分既要符合实际的充电服务网络又要达到简化问题的目的[14]。

1.2　数学模型的建立

科学、合理、可行的充电服务网络，不仅能够推进电动汽车市场化，而且还能够兼顾充电需求和资源利用，既能使电动汽车的充电需求得到满足，方便电动汽车用户充电，还能够合理利用资源，减少资源的浪费[15]。考虑到充电站布局规划的基本原则和影响因素，在此基础上建立充电成本最小化的电动汽车充电站布局规划模型。其数学模型描述如下：

(1)

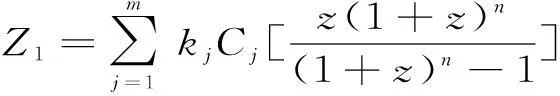
(2)

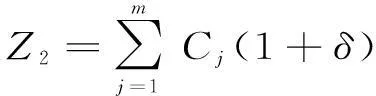
(3)

(4)

式中：Z1表示充电站建设的投资的固定成本；Z2表示充电站运行和维护的成本；Z3表示充电用户的充电成本。m表示建设的充电站的数量；Cj表示充电站的建设成本；z表示贴现率；n表示投资回收年限；kj表示0～1变量，如果kj=1则表示第j个候选站被选中，否则kj=0；δ表示折算系数；c0表示单位车辆单位距离的损耗费用；Ny表示每年的天数；Td表示平均每个充电用户的日充电次数。

(5)

其中：h1表示电动汽车百公里耗电；h2为电动汽车平均日行驶路程；q表示电动汽车电池的容量。Ij表示充电小区i内的充电用户到充电站j充电的集合。gij为0～1变量，约束充电需求小区i内的充电用户在某时段只到第j个充电站进行充电。gij=1代表充电需求小区i内的充电用户到充电站j充电。gij=0 代表充电需求小区i内的充电用户不到充电站j充电。

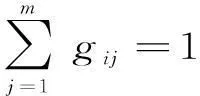
(6)

Dij充电需求小区i的集合中心到候选站j的距离；ηij表示路况系数；Wi表示充电小区i内电动汽车的保有量。

1.3　约束条件

考虑到实际情况，比如充电容量和用户的方便性，充电站布局规划模型还需要加入以下约束条件。

(1)充电站充电容量约束

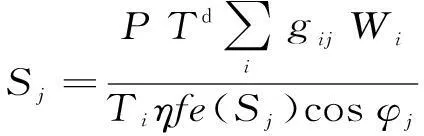
(7)

(8)

式中：Sj表示第j个充电站的配电量；P表示单个电动汽车的充电功率；Ti表示每日第i种充电模式下的充电时间；η表示充电的效率；f表示充电机的需用系数；e(Sj)表示充电站的负载率；cosφj表示充电站的功率因数。

(2)充电站服务半径约束

(9)

式中：充电站的服务半径约束用R表示。

联合公式(1)、(5)、(6)、(9)，构建充电站布局最优规划的数学模型，其中构建的模型中有很多的变量，包括电动汽车充电用户组成的离散变量、充电站需求量等整数变量。传统的优化算法很难求解这样复杂的问题，本文选择遗传算法进行求解。

2遗传算法的应用

遗传算法是模拟生物在自然环境中优胜劣汰、适者生存的遗传和进化过程而形成的一种自适应能力的、全局性的概率搜索算法[16]。通过模拟生物进化中优胜劣汰、适者生存的原理，进行编码与进化寻优，末代种群中的最优个体经过解码可以作为问题的近似最优解[16]。遗传算法没有连续和导数存在的要求，搜索空间没有限制。

2.1　染色体编码

采用二进制为染色体编码，编码串为A={aj,i=1,2,…,n}，A为维实向量，n为充电需求小区的个数，aj=gijj(j=1,2,… ,m)，m为充电站的个数，gij为0～1变量，约束充电需求小区i内的充电用户在某时段只到第j个充电站进行充电，则充电站的个数为

(10)

式中：f1表示充电站的同时率；[]表示取整数。

2.2　适应度函数

适应度函数也叫评价函数，根据目标函数可以确定适应度函数[17]。遗传算法常常将目标函数直接作为适应度函数，但是由于在执行操作时，它要求与个体适应度成正比的概率来决定当前群体中每个个体遗传到下一代群体中的概率，要正确计算概率，要求所有个体适应度函数值必须非负[18]。把目标函数当作适应度函数，不用再进行求导等数学运算，由以上可知，本文的目标函数就是最小化问题，可以进行适当的转化，即Fit(Z)=-Z。

则适应度函数为：

(11)

式中：cmax为Z的最大估计值。

3遗传算法的终止原则和最优解的确定

3.1　终止原则

考虑到充电站布局规划的模型的情况，关于遗传算法有3种终止原则：

(1)如果在事先选择的最大迭代次数之内获得最优解，就停止迭代；

(2)如果到了事先选择的最大的迭代次数即停止迭代；

(3)在可能得不到最优解的情况下，满足以下收敛准则就停止运行。

通常收敛准则可以定义为：

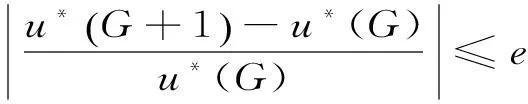
(12)

式中：第G代最优个体的适应度用u*(G)表示。

3.2　确定最优解的方法

遵循上面遗传算法的终止原则，相应确定最优解可以参照以下标准：

(1)群体中最好的为最优解。

(2)最优解可以是在群体中挑选出的最好的。

(3)最优解可以是满足条件的那个。

还有一种情况就是得到很多个最优解或者满意解，这个时候就要根据实际情况选择。

算法流程如图1。

4算例分析

某规划区的面积为10.5 km2，在规划的时间范围内电动汽车的保有量是2 190辆，目前已知的是规划区已经按照用地性质、道路等因素划分了20个充电需求小区。充电需求小区内几何中心的坐标和电动汽车的数量如表1所示。先假设在充电站规划这段时间之内电动汽车的数量恒定，每天快速充电的用户比例是80%，常规充电的用户的比例是20%，充电功率设定为20 kW，平均每辆电动汽车两天充一次电。现在规划区域内计划建设5个充电站，已经考虑了所有的情况，候选站址的具体位置见表2。

图1　遗传算法流程图

表1　电动汽车保有量和小区的几何中心　km

表2　候选站址的地理位置　km

电动汽车充电需求小区和候选充电站分布如图2。

参数取值如表3。

初步搜索寻优以式(1)为目标函数，式(6)～(9)为约束条件进行遗传编码，采用Matlab编写程序，最后运行得到模型的优化结果，候选站址和其服务范围见表4。

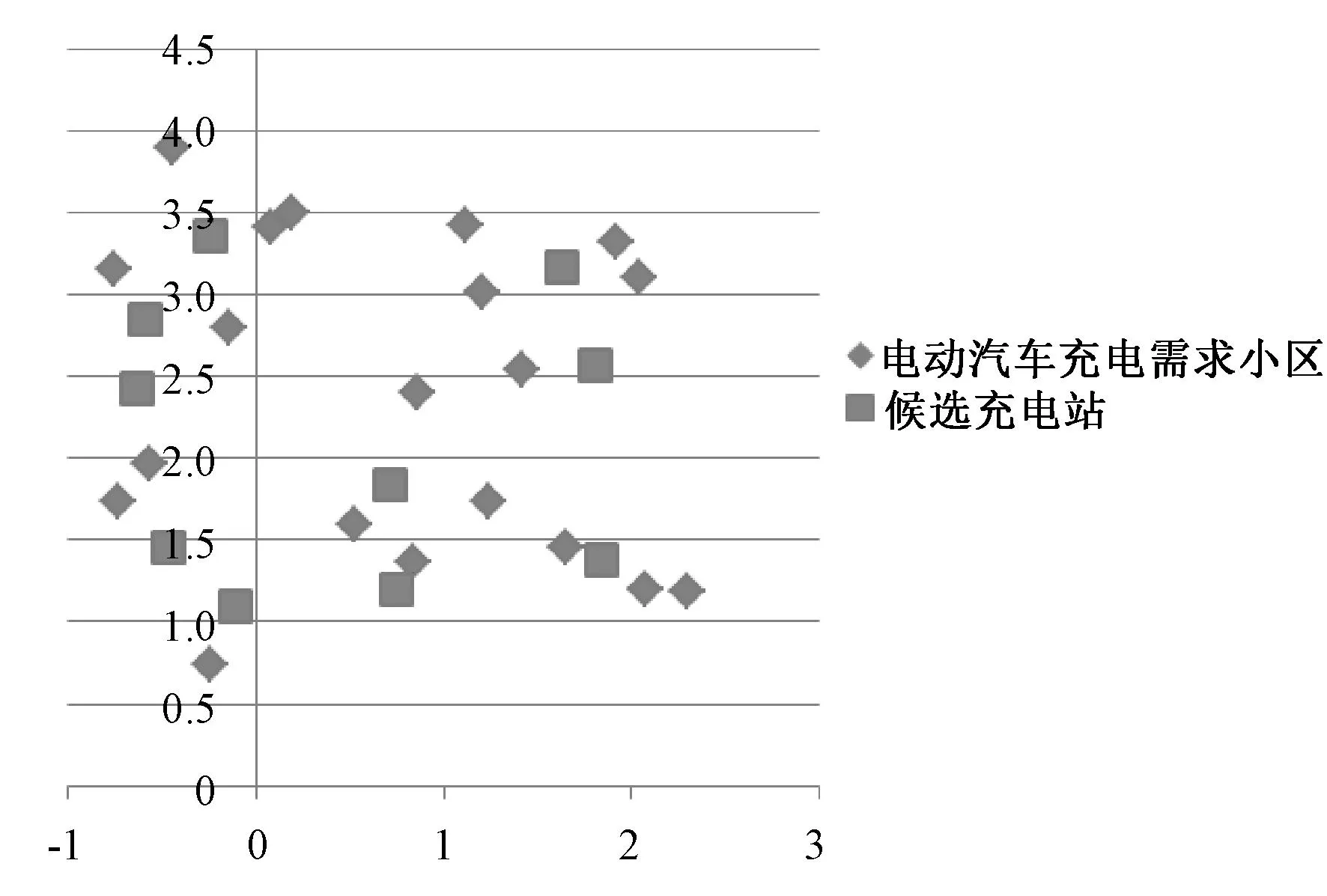
图2　电动汽车充电需求小区和候选充电站分布图

优化后的充电站及其服务的充电需求小区见图3。

从表4可以得出，充电需求小区内的几何中心基本上可以代表充电站的站址，规划区域内的2 190辆电动汽车的充电需求可以用这5座充电站来满足，总年费用为1 122.27万元。从表中的数据也可以看出，每个充电站服务的车辆并不相同，所以规划的充电站的容量也不一样，这样建设的充电站科学合理。

表3　参数取值表

表4　优化后的站址及其服务范围　km

图3　优化后的充电站及其服务的充电需求小区

5结论

充电站的布局规划涉及很多的部门，工程量非常大，所以在建设的过程中要考虑建设的成本，站在方便用户的角度，通过科学规划可以做到节约资源。本文基于电动汽车充电站布局规划相关研究现状，对所要规划的区域进行充电需求小区的划分，建立年费用函数最小模型，利用遗传算法求得满意解，使规划区域内电动汽车充电用户充电需求都得到了满足。从算例分析得出，本文采用的方法和模型是有一定的科学性的。但是充电站布局规划涉及的面很广，还需要在实际布局规划过程中根据实际情况合理确定充电站的规模和站址。

参考文献:

[1]Ruhl C. BP世界能源统计年鉴2014 [M] .英国石油公司, 2014.

[2]赵玲.济南市车用天然气需求预测及加气站选址研究[D] .济南：山东大学，2008.

[3]Q/GDW478-2010,电动汽车充电设施建设技术导则[S] .

[4]胡天娇，甄翠敏.国内外电动汽车基础设施建设运营[J] .河北联合大学学报(社会科学版)，2014，14(1)：54-56.

[5]王辉.电动汽车充电站规划与运营研究[D].杭州：浙江大学，2013.

[6]王阳.纯电动公交车充电需求特性及充电设施规划方法的研究[D] .北京：华北电力大学，2012.

[7]王飞龙，孙凯航，李燕青.基于用户分类的电动汽车充电站需求预测[J] .黑龙江电力，2013，35(2)：132-134.

[8]张成，滕欢.电动汽车充电站规划模型及评价方法[J].电力系统及其自动化学报，2014，28(1)：49-52.

[9]王泽黎，齐灿.电动汽车充电站最优规模和布局[J] .电力建设，2014，35(4)：132-136.

[10]葛少云，冯亮，刘洪，等.电动汽车充电站规划布局与选址方案的优化方法[J] .中国电力，2012，45(11)：96-101.

[11]孙小慧.考虑时空限制的电动汽车充电站布局模型[D] .大连：大连理工大学，2012.

[12]林琳，高亚静.基于排队理论的充电站最优配置[J].电力科学与工程，2014,30(4):33-37.

[13]吴春阳.电动汽车充电设施规划、接入及智能响应[D] .郑州：郑州大学，2011.

[14]何战勇.电动汽车充电站规划方法及运营模式研究[D] .北京：北京交通大学，2012.

[15]熊虎，向铁元，祝勇刚，等.电动汽车公用充电站布局的最优规划[J] .电力系统自动化，2012，(23):65-70.

[16]边霞，米良.遗传算法理论及其应用研究进展[J] .计算机应用研究，2010，27(7)：2425-2429.

[17]王进强，陈少华.基于改进遗传算法的含分布式电源的配电网故障定位[J].电力科学与工程，2013，29(12)：13-17.

[18]唐连生，李思寰，张雷.物流系统优化与仿真[M] .北京：中国物资出版社，2013.

Based on Genetic Algorithm Optimal Layout of Electric Vehicle Charging Station

Liu Fei

(Beijing Wuzi University，Beijing 101149，China)