板块运动几何模型的比较
吕志鹏
(中国地震局第一监测中心,天津 300180)
Comparison of Plate Motion Geometry Models
LV Zhipeng
板块运动几何模型的比较
吕志鹏
(中国地震局第一监测中心,天津 300180)
Comparison of Plate Motion Geometry Models
LV Zhipeng
摘要:基于空间大地测量数据建立板块运动的欧拉矢量具有更优的现势性。本文对其计算的3种几何模型进行了理论分析,并且利用IERS发布的ITRF2000速度场数据对上述3种几何模型进行了比较。结果表明,3种几何模型得到的板块运动的欧拉矢量具有统计一致性。但是,由它们得到的板块运动的欧拉矢量最大差异约1 mm/a,整体旋转量最大差异约0.2 mm/a,这对于高精度的大地测量和地球动力学应用影响显著。朱文耀等采用的几何模型更加合理,拟合精度更高,因而建议利用该模型进行板块运动欧拉矢量的拟合。
关键词:板块运动;空间大地测量;几何模型;差异;ITRF2000
一、引言
20世纪初Wegener提出了大陆漂移假说,随后地幔对流假说和海底扩张假说的提出为其提供了理论支持。直到20世纪60年代末,Morgan、Le Pichon和Mckenzie根据掌握的全球海岭、海沟、转换断层、地磁条带异常图像和地震等方面的资料,对海底扩张假说进行了论证,明确了岩石圈和软流圈的概念,从而提出了岩石圈由悬浮在软流圈的若干活动块体组成的板块构造学说。自此构造板块运动的定量分析成为地球动力学研究的热点问题。对板块运动的定量分析采用两种方法:①地质与地球物理方法;②空间大地测量方法。地质与地球物理方法利用板块扩张速度、转换断层方位角、地震滑移矢量等观测数据通过加权最小二乘法[1-2]拟合刚体板块运动的相对欧拉矢量。不同板块运动模型[3-4]建立过程中的主要区别在于:①观测数据种类、数量、精度及预处理方式;②数学模型的选择;③板块的划分方式。Minster和Argus分别于1978年和1991年基于热点(hotspot)假说和无净旋转(no-net-rotation)条件建立起了板块运动的绝对模型AM0-2[5]和NNR-NUVEL-1[6],为地球动力学研究提供了绝对的速度场基准。随着空间大地测量技术VLBI(very long baseline interferpmetry)、SLR(satellite laser ranging)、GNSS(global navigation satellite system)和DORIS(doppler orbitpgraphy and radio-position integrated by satellite)技术的发展和观测精度的提高,使得利用空间大地测量数据建立板块运动模型成为可能[7-10]。相对于几百万年尺度的地质与地球物理板块运动模型,基于空间大地测量数据建立的板块运动模型反映几十年尺度的板块运动模式。不同学者对利用空间大地测量数据建立板块运动模型过程中的各种影响因素,如原始数据协方差阵、台站的选择、绝对运动模型的约束条件和板块的划分方式等,进行了初步的分析[8,11-12],取得了诸多有益成果。
本文在已有研究工作基础之上对基于空间大地测量数据建立板块运动模型的3种几何模型[7-10]进行深入分析,然后根据IERS公布的ITRF2000速度场数据对上述3种几何模型进行精度分析,从而获得性能最优的几何模型。
二、几何模型描述
在用空间大地测量数据建立板块运动模型时,通常假设板块的运动服从欧拉定理,即刚体板块在地球表面绕某一固定轴做旋转运动。其数学形式如下
V=ω×r
(1)
式中,V为板块上观测台站的速度;ω为板块绕固定轴旋转的角速度;r为板块上观测台站的位置矢量。不同的几何模型的本质区别在于V和r的形式不同。
1. 几何模型1
Altamimi等[7]根据ITRF2000速度场建立了ITRF2000-PMM速度场模型,采用的几何模型如下
(2)
式中,(VX,VY,VZ)为板块上观测台站在地心直角坐标系下的速度;(X,Y,Z)为板块上观测台站在地心直角坐标系下的位置;(ωX,ωY,ωZ)为板块在地心空间直角坐标系下的角速度。根据欧拉定理,如果在板块上有两个及以上的观测台站,板块运动的欧拉矢量ω就可以用加权最小二乘法求得。此时,可以同时估计多个板块的欧拉矢量或单独估计每个板块的欧拉矢量。
2. 几何模型2
朱文耀等[8]利用ITRF2000速度场计算板块运动的欧拉矢量时,将刚体板块上观测台站的速度V分解为
V=Vh+Vt+Vr
(3)
式中,Vt和Vr代表冰后反弹速度和板块内形变速度;Vh为观测台站的水平速度,其具体形式如下
(4)
将式(4)代入式(1)可得几何模型
(5)
式中,(VX,h,VY,h,VZ,h)为板块上观测台站在地心直角坐标系下的水平速度;其他参数意义同上。同样可以采用加权最小二乘法获得板块运动的欧拉矢量ω。由于将观测台站的速度转换为水平速度,故需要对观测台站的权矩阵进行变换,即
Ph=B·P·BT
(6)
式中,P和Ph分别为观测台站在地心直角坐标系下速度和水平速度的权矩阵;B为转换阵,其具体形式如下
(7)
3. 几何模型3
金双根等[9]和朱新慧等[10]分别利用ITRF2000和ITRF2005速度场计算板块运动的欧拉矢量,将地心直角坐标系下的速度转换为站心直角坐标系下的速度,即
Vl=T·V
(8)
式中,V和Vl分别为观测台站在地心直角坐标系下和站心直角坐标系下速度;T为转换矩阵,其具体形式如下
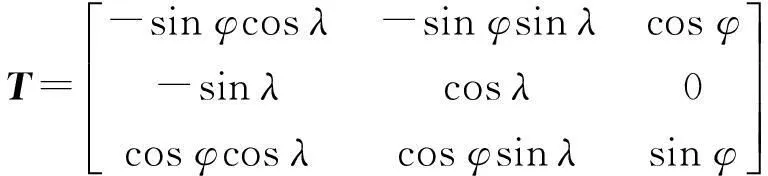
(9)
式中,φ、λ为观测台站的大地纬度和大地经度。同时,需要将观测台站的权矩阵转换到站心坐标系下
Pl=T·P·TT
(10)
式中,Pl为观测台站在站心直角坐标系下的权矩阵。
将站心直角坐标系下的速度Vl代入式(1)可得几何模型
(11)
式中,Ve和Vn为观测台站在站心直角坐标系下速度Vl的东向分量和北向分量;r为地球的平均曲率半径。根据式(11)利用加权最小二乘法可以求得板块运动的欧拉矢量。
三、数据分析
板块运动欧拉矢量的计算需要高精度的速度场,并且观测台站观测连续并且构造稳定。在此采用ITRF2000核心站速度场建立板块运动的欧拉矢量。观测台站的选择需要满足如下条件:①观测台站至少连续观测3年;②观测台站位于刚体板块上,远离地震带或变形区;③观测台站速度的形式误差优于3 mm/y;④观测台站至少3种技术解的速度残差优于3 mm/y。同时,由于Bahrein和Easter Island观测台站与NNR-NUVEL1A地质与地球物理模型的差异分别达到6 mm/y和10 mm/y,Tromsoe和Flin-Flon观测台站在欧拉矢量计算中残差达到2 mm/y,剔除上述4个观测台站。为了兼顾观测台站的均衡性加入O’Higgins和Haleakala 2个观测台站。最终,笔者利用52个观测台站计算板块运动的欧拉矢量(如图1所示)。
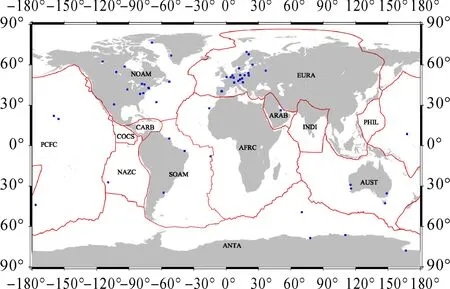
图1 计算板块运动欧拉矢量的观测台站分布
利用上述3种几何模型,可以得到ANTA(Antarctica)、AUST(Australia)、EURA(Eurasia)、NOAM(North America)、SOAM(South America)和PCFC(Pacific)6个板块的欧拉矢量,见表1。ARAB(Arabia)、AFRC(Africa)、NAZC(Nazca)板块由于只有一个观测台站无法获得欧拉矢量。COCO(Cocos)、JUFU(Juan de Fuca)、PHIL(Philippine)、INDI(India)板块由于没有观测台站分布也无法获得欧拉矢量。
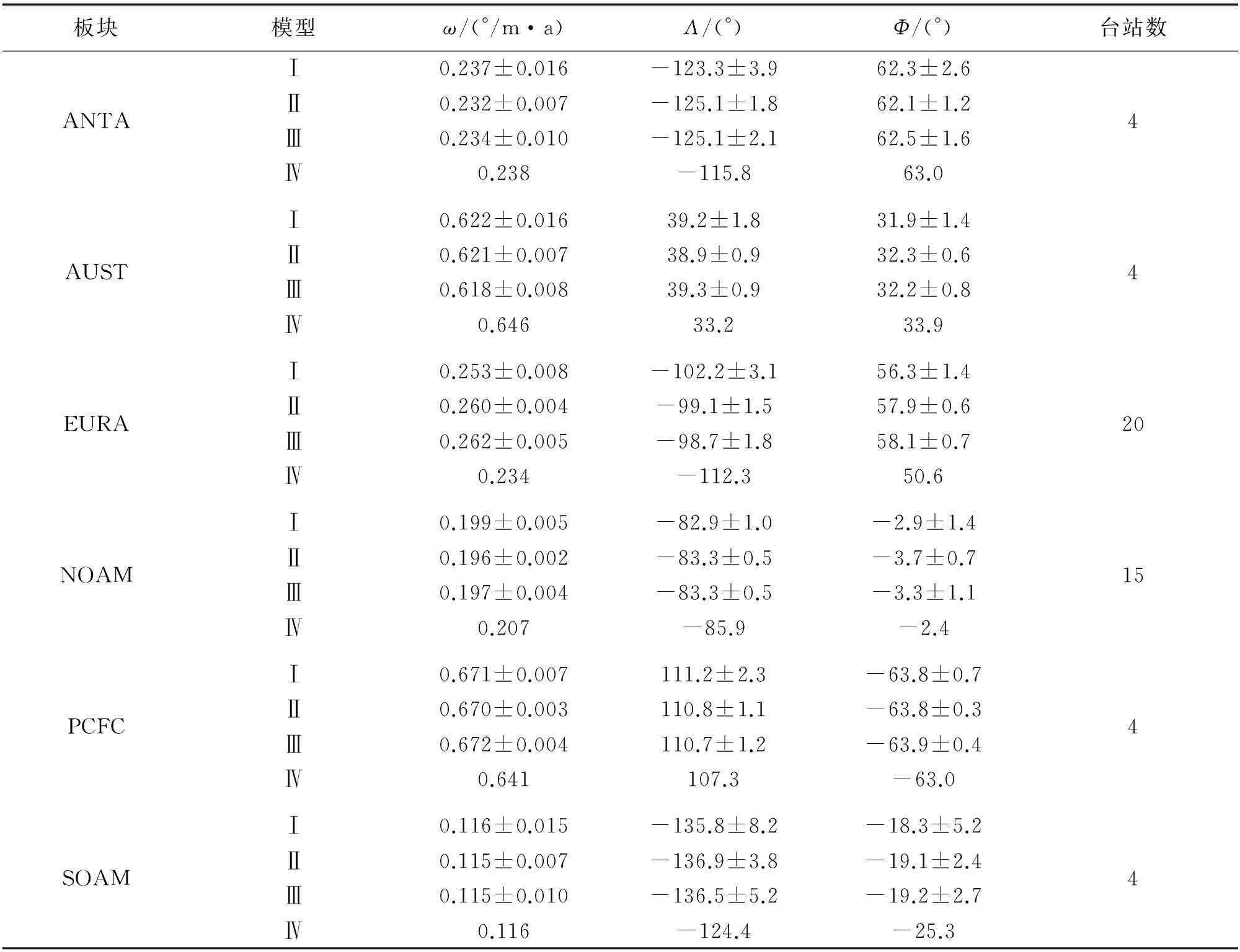
表1 不同几何模型得到的板块运动欧拉矢量
注:Ⅰ代表几何模型一得到的板块运动欧拉矢量;Ⅱ代表几何模型二得到的板块运动欧拉矢量;Ⅲ代表几何模型三得到的板块运动欧拉矢量;Ⅳ代表NNR-NUVEL1A模型。
由表1中可知,3种几何模型均可以互相落在99%的置信区间内。除EURA板块几何模型1无法落在几何模型2和几何模型3的95%的置信区间外,3种几何模型均可以互相落在95%的置信区间内。因而,总的来说3种几何模型具有统计上的一致性。同时,几何模型2和几何模型3可以互相落在68%的置信区间内,说明它们统计一致性更优。对3种几何模型的拟合精度进行考察可以发现,几何模型2的精度略高于几何模型3,且显著高于几何模型1。通过对3种几何模型结构进行分析可知,几何模型1采用的速度为观测台站在空间直角坐标系中的速度,这一速度融合了板块在垂直方向的速度分量,而这一速度分量在板块欧拉矢量的计算中并不考虑。这就造成了几何模型1的拟合精度显著下降。而几何模型2通过式(4)剔除了速度垂直分量的影响,拟合精度显著上升。相对于几何模型2,几何模型3中将地球视为绝对的球体进行欧拉矢量的计算。然而,地球表面不同观测台站的向径存在差异,因而模型3也具有理论缺陷。
上述3种几何模型计算得到的板块旋转量最大差异为0.032 4 mas/a,这等价于板块整体旋转约1 mm/a。这对于毫米级甚至亚毫米级的大地测量和地球动力学应用影响显著。例如,现今的GNSS速度场结算精度已经达到毫米甚至亚毫米级,板块运动的欧拉矢量的差异会影响速度场约束的精度和形变分析的结果。
接下来利用Argus等[6]发布的板块转动惯量数据,计算上述3种几何模型得到的板块欧拉矢量的整体旋转量,见表2—表4。笔者已经获得ANTA、AUST、EURA、NOAM、SOAM和PCFC 6个板块的欧拉矢量,对于其他板块的欧拉矢量,可以通过下述方法获得:
1) 直接采用NNR-NUVEL1A模型的欧拉矢量。
2) 对于每一个未获得欧拉矢量的板块m,其欧拉矢量ωm如下
ωm=ωpm+ωp
(12)
式中,ωp是板块p的欧拉矢量;ωpm是板块相对模型NUVEL1A中的板块p相对于板块m的相对欧拉矢量。因而,对于每一个未获得欧拉矢量的板块,可以通过ANTA、AUST、EURA、NOAM、SOAM和PCFC 6个板块获得6个欧拉矢量。
3) 将步骤2)中的6个欧拉矢量做平均作为板块的欧拉矢量。
4) 根据式(12),采用EURA板块计算AFRC和ARAB板块的欧拉矢量;采用NOAM板块计算CARB板块的欧拉矢量;采用PCFC板块计算NAZC、COCO、JUFU、PHIL板块的欧拉矢量;采用AUST板块计算INDI板块的欧拉矢量。

表2 几何模型1不同方法得到的整体旋转

表3 几何模型2不同方法得到的整体旋转

表4 几何模型3不同方法得到的整体旋转
对表2、表3、表4进行综合分析可知,几何模型2得到的整体旋转量小于其他两种几何模型。不同算法得到的整体旋转量最大差异为0.006 6 mas/a,这等价于板块整体旋转约0.2 mm/a,这对于亚毫米级的大地测量和地球动力学应用影响显著。例如,基于空间大地测量技术的长期极移监测显示,极点在73.9°±0.03°方向上以4.123±0.002 mas/a移动[13-14]。因而,上述几何模型的差异造成的参考系统的整体旋转大于极移监测的精度水平。
四、结束语
基于空间大地测量数据建立板块运动的欧拉矢量,相对于地质与地球物理方法更具现势性。Altamimi等[7]、朱文耀等[8]、金双根等[9]和朱新慧等[10]分别采用了不同的几何模型拟合板块运动的欧拉矢量。本文利用上述模型对ITRF2000核心站速度场进行分析,虽然这3种几何模型计算得到的欧拉矢量统计上具有一致性,但是朱文耀等[8]采用的几何模型更加合理,拟合精度更高。同时,由于不同几何模型计算得到的欧拉矢量最大差异约1 mm/a,整体旋转量最大差异约0.2 mm/a,这对于高精度的大地测量和地球动力学应用影响显著。因此,在利用空间大地测量数据建立板块运动的欧拉矢量时,建议利用朱文耀等[8]采用的几何模型。
参考文献:
[1]CHASE C G. The N Plate Problem of Plate Tectonics[J]. Geophysical Journal International, 1972, 29(2): 117-122.
[2]MINSTER J B, JORDAN T H, MOLNAR P, et al. Numerical Modelling of Instantaneous Plate Tectonics[J]. Geophysical Journal International, 1974, 36(3): 541-576.
[3]秦小军, 周硕愚, 吴云. 现今板块、块体运动定量模型的发展[J]. 大地测量与地球动力学, 1999, 19(2): 90-97.
[4]朱新慧, 孙付平, 王刃. 现今板块运动模型的发展及其比较[J]. 测绘科学技术学报, 2010, 27(3): 184-188.
[5]MINTER J B, JORDAN T H. Present-day Plate Motions[J]. Journal of Geophysical Research: Solid Earth (1978—2012), 1978, 83(B11): 5331-5354.
[6]ARGUS D F, GORDAN R G. No-net-rotation Model of Current Plate Velocities Incorporating Plate Motion Model NUVEL-1[J]. Geophysical Research Letters, 1991, 18(11): 2039-2042.
[7]ALTAMIMI Z, SILLARD P, BOUCHER C. ITRF2000: A New Release of the International Terrestrial Reference Frame for Earth Science Applications[J]. Journal of Geophysical Research: Solid Earth (1978—2012), 2002, 107(B10): ETG 2-1-ETG 2-19.
[8]朱文耀, 符养, 李彦,等. ITRF2000的无整体旋转约束及最新全球板块运动模型NNR—ITRF2000VEL[J]. 中国科学:D辑, 2003, 33(B04):1-11.
[9]金双根, 朱文耀. 基于 ITRF2000 的全球板块运动模型[J]. 中国科学院上海天文台年刊, 2002(23): 28-33.
[10]朱新慧, 孙付平, 王刃. 基于ITRF2005的全球板块运动模型[J]. 地球物理学进展, 2009 (3): 859-865.
[11]金双根, 朱文耀. 3 种板块绝对运动模型的建立及其比较[J]. 中国科学院上海天文台年刊, 2002 (23):21-27.
[12]张西光, 吕志平, 赵冬青. NNR 条件, ITRF 和全球板块运动模型[J]. 大地测量与地球动力学, 2007, 27(3): 39-43.
[13]GROSS R, VONDRAK J. Astrometric and Space-geodetic Observations of Polar Wander[J]. Geophysical Research Letters,1999,26(14):2085-2088.
[14]HOPFNER J. Chandler and Annual Wobbles Based on Space-geodetic Measurements[J]. Journal of Geodynamics, 2003, 36(3): 369-381.
[15]梁洪宝, 朱爽, 王友, 等. 陆态网络 GNSS 基准站阶跃偏移量的精确估计[J]. 震灾防御技术,2014,9(B10):622-631.
[16]杨建会, 聂桂根, 薛长虎. 基于GPS数据的川滇地区地壳水平运动研究[J]. 测绘通报, 2015(6):28-31,56.
[17]程鹏飞,成英燕,秘金钟,等. CGCS2000板块模型构建[J]. 测绘学报, 2013, 42(2): 159-167.
作者简介:吕志鹏(1988—),男,硕士,工程师,从事地球参考框架建立与维持的研究。E-mail:lvzhipeng2007@gmail.com
基金项目:中国地震局地震行业科研专项(201308009); 中国地震局地震科技星火计划(XH2015060Y);中国地震局青年震情跟踪课题(2015010211); 中国地震局第一监测中心科技创新主任基金(FMC2015001)
收稿日期:2015-06-16; 修回日期: 2015-08-08
中图分类号:P228.4
文献标识码:B
文章编号:0494-0911(2015)12-0015-05
DOI:引文格式: 吕志鹏. 板块运动几何模型的比较[J].测绘通报,2015(12):15-19.10.13474/j.cnki.11-2246.2015.367

