无迹卡尔曼滤波衰减记忆算法研究
王 仁,赵长胜,夏志浩,谭兴龙,孙 鹏
(1. 江苏师范大学城建与环境学部, 江苏 徐州 221116; 2. 常州金坛区规划局,江苏 常州 213200;
3. 江苏师范大学测绘学院,江苏 徐州 221116)
Study of Attenuation Memory Unscented Kalman Filtering Algorithm
WANG Ren,ZHAO Changsheng,XIA Zhihao,TAN Xinglong,SUN Peng
无迹卡尔曼滤波衰减记忆算法研究
王仁1,赵长胜1,夏志浩2,谭兴龙3,孙鹏1
(1. 江苏师范大学城建与环境学部, 江苏 徐州 221116; 2. 常州金坛区规划局,江苏 常州 213200;
3. 江苏师范大学测绘学院,江苏 徐州 221116)
Study of Attenuation Memory Unscented Kalman Filtering Algorithm
WANG Ren,ZHAO Changsheng,XIA Zhihao,TAN Xinglong,SUN Peng
摘要:无迹卡尔曼滤波算法作为典型的卡尔曼滤波改进算法,有效地解决了线性化时高阶项的舍弃误差和强非线性模型的无法线性化问题。但是常规的无迹卡尔曼滤波对旧的数据和当前数据的利用率是相同的,很容易导致滤波的发散。通过引进衰减因子加强了对当前数据的利用,降低了旧数据对滤波结果的影响。本文基于此提出了衰减记忆无迹卡尔曼滤波算法,并对衰减因子的确定进行了分析。仿真试验分析表明,衰减记忆无迹卡尔曼滤波算法能够提高滤波结果的精度。
关键词:无迹卡尔曼滤波;衰减因子;衰减记忆无迹卡尔曼滤波
一、引言
自1960年卡尔曼(R.E.Kalman)提出了卡尔曼滤波理论以来,这一理论就被广泛应用于各个领域,如动态导航定位、目标跟踪、卫星姿态确定等。但是随着应用的广泛性,卡尔曼滤波的弊端也凸显出来,因为在很多领域绝大多数是以非线性系统存在的,而卡尔曼滤波算法是针对线性系统的。因此有学者提出了扩展卡尔曼滤波算法,即把非线性系统方程线性化,一些问题得到了解决。但是在线性化时高阶项的舍弃,以及有些非线性系统的强非线性使扩展卡尔曼滤波也遇到了一些问题,此时有学者又提出了无迹卡尔曼滤波算法。无迹卡尔曼滤波算法通过某种确定性采样策略生成一组符合原状态分布的Sigma点集,再利用无迹变换(unscented transformation,UT)对这些点进行非线性变换,然后再来估计系统状态的估值及其协方差矩阵。常规的无迹卡尔曼滤波的当前观测数据与旧观测数据的使用程度是相当的,但是随着观测的进行,滤波模型很难准确地描述目标每一时刻的运动状态,使得状态估计太依赖于过去的数据,从而导致了滤波发散。基于此,本文提出了用衰减因子来限制旧观测数据的使用程度,可以有效提高计算结果的精度。
二、常规无迹卡尔曼滤波的计算过程
一般情况下,系统状态方程只考虑线性的,观测方程为非线性的。已知在tk时刻,有状态方程和观测方程分别为
Xk=Φk,k-1Xk-1+wk
(1)
Lk=h(Xk)+ek
(2)
式中,状态方程为线性函数,观测方程为非线性函数;Xk为tk时刻n×1维状态向量;Φk,k-1为状态转移矩阵;Lk为tk时刻m×1维观测向量;h(Xk)为非线性观测函数;wk和ek分别为n×1维状态噪声向量和m×1维观测噪声向量,均为加性高斯白噪声,二者的协方差矩阵分别为Qk和Rk,且互不相关。
无迹卡尔曼滤波算法的具体步骤如下:
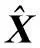
(3)
(4)
3) 通过非线性观测方程对Sigma点集χk进行非线性变换,得到新的Sigma点集,即预测观测向量
(5)
新的Sigma点集对应的均值权值和方差权值不变,仍为Wm和Wc,则有
(6)
(7)
(8)
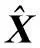
(9)
(10)
(11)
三、衰减记忆无迹卡尔曼滤波的计算过程
由上所述,无迹卡尔曼滤波的计算结果是在同种程度地依靠观测向量中所含各个时刻下的数据的基础上得出的。因此,旧数据在滤波中起到了过强的牵制作用,而由当前数据所给出的新信息对于一步预测值的修正作用则受到过强的抑制,致使滤波值不能较好地跟踪真值变化。衰减记忆无迹卡尔曼滤波算法利用衰减因子α>1限制卡尔曼滤波器的记忆长度,使得滤波过程更加重视新信息的利用,而降低了对旧数据的依赖性。具体来说,就是用衰减因子α对状态方差阵初值和噪声序列的既往值(它们反映了相应时刻数据对滤波值的作用大小)进行如下处理
用这种新的方差序列导出的衰减记忆滤波算法为:
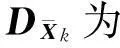
(12)
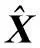
四、衰减因子的确定
衰减因子的取值对滤波结果影响很大,本文通过迭代计算来确定最优取值。衰减因子的取值范围α>1,可以分别取值以确定。根据α取1.0、1.1、1.15、1.2、1.25、1.3和1.4算得的结果如图1所示,经过比较分析本论文α取1.23时,滤波的结果最优。
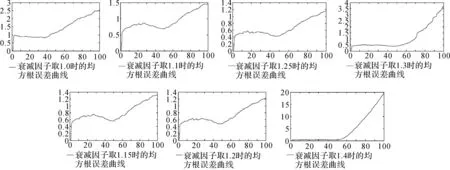
图1 衰减因子取不同值的计算结果
五、仿真试验分析
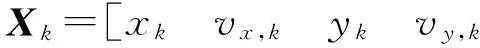
Xk+1=Φk+1,kXk+wk
(13)
(14)
其中
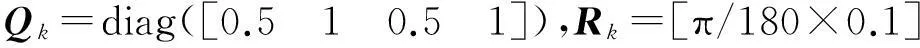
无迹卡尔曼滤波算法和衰减记忆无迹卡尔曼滤波算法的处理结果如图2所示。
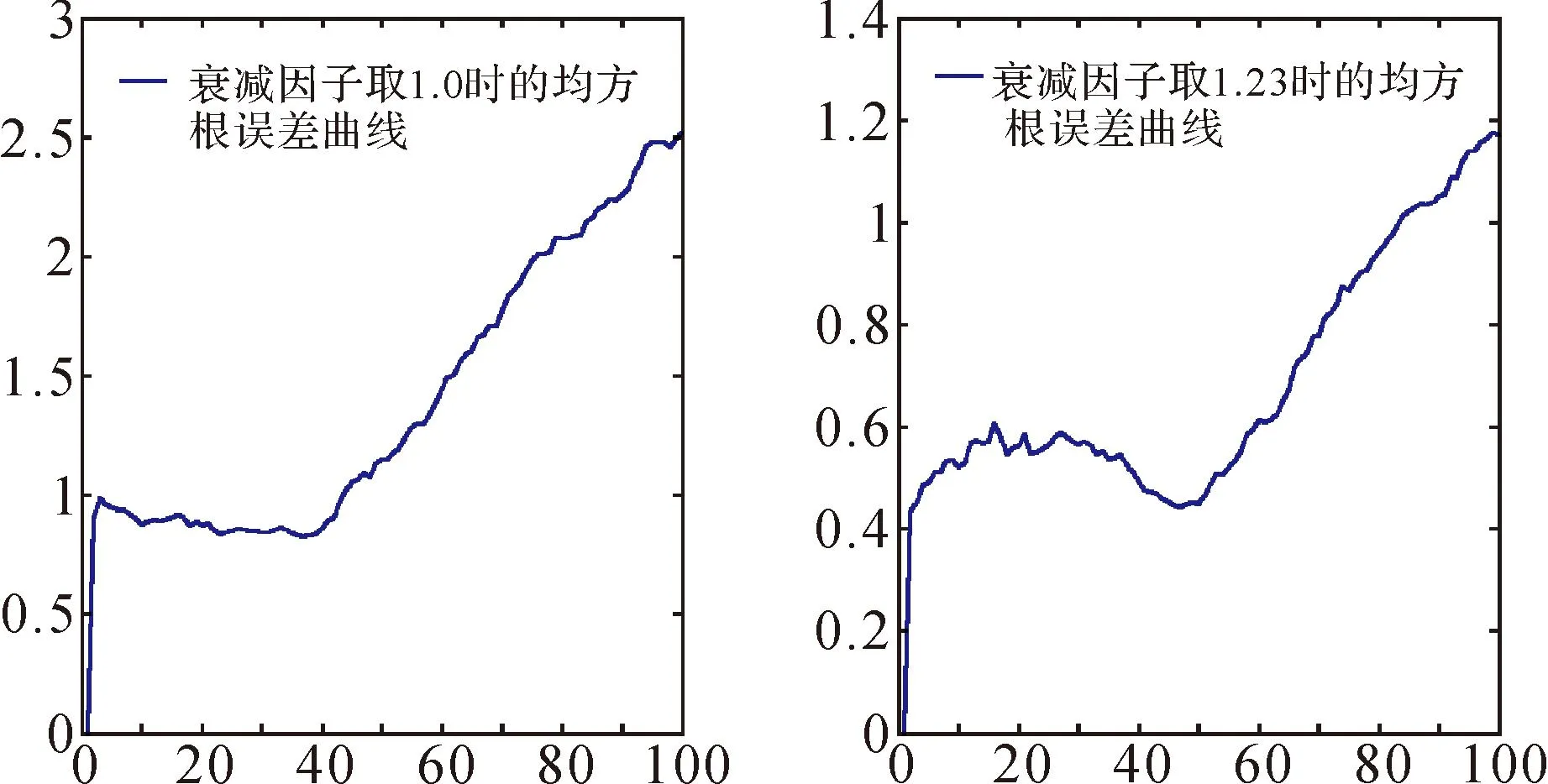
图2 仿真数据计算的结果
六、结束语
衰减记忆无迹卡尔曼滤波算法由于衰减因子的引入,对旧数据对滤波的结果进行了限制,凸显了新数据(当前数据)的作用。通过仿真试验结果的分析可以充分认识到,衰减记忆无迹卡尔曼滤波算法比无迹卡尔曼滤波算法更容易收敛且计算结果的精度更高。当然衰减因子的选取对数据处理结果也影响较大,通过迭代计算总能找到比较适合的衰减因子。
参考文献:
[1]杨元喜.自适应动态导航定位[M].北京:测绘出版社,2006:141-145.
[2]赵长胜.有色噪声滤波理论与算法[M]. 北京:测绘出版社,2010:153-155.
[3]万某峰,赵长胜.UKF滤波中蒙特卡洛采样策略比较分析[J].测绘通报,2012(12):37-39.
[4]万某峰.抗差自适应无迹卡尔曼滤波算法研究[D].徐州:江苏师范大学,2012.
[5]李莉.衰减记忆扩展卡尔曼滤波在目标跟踪中的应用[J].电子测量技术,2011(2):36-38.
[6]傅建国,王孝通,金良安,等.Sigma点卡尔曼滤波及其应用[J].系统工程与电子技术,2005(1):141-144.
通信作者:赵长胜
作者简介:王仁(1990—),男,硕士生,主要研究方向为GNSS数据处理理论及应用。E-mail:wangr1990322@163.com
基金项目:国家自然科学基金(41174032);江苏省自然科学基金(BK20150236);江苏师范大学研究生科研创新计划重点项目(2015YZD004)
收稿日期:2014-09-25
中图分类号:P228
文献标识码:B
文章编号:0494-0911(2015)12-0020-03
引文格式: 王仁,赵长胜,夏志浩,等. 无迹卡尔曼滤波衰减记忆算法研究[J].测绘通报,2015(12):20-22.DOI:10.13474/j.cnki.11-2246.2015.368

