人均住房面积与恩格尔系数关系分析

刘超

摘要：恩格尔系数是对居民生活水平的重要反映，即恩格尔系数小的家庭拥有更好的经济条件。此外，居民生活水平提高的同时，也对住房提出更高的要求。为此，本文试图对人均住房面积与恩格尔系数之间的关系进行实证分析。

关键词：人均住房面积；恩格尔系数；线性关系；Granger因果关系

中图分类号：F407.9 文献识别码：A 文章编号：1001-828X（2016）001-00000-01

一、引言

住房主要用来满足居民的生存、发展与享受需要，而居民对住房的要求直接体现出居民生活水平的高低。恩格尔系数是食品支出总额占个人消费支出总额的比重，同时也是居民生活水平的重要指标，因此透过恩格尔系数可分析出家庭的富足程度、生活水平、住房要求及住房面积。依此内容，本文实证分析人均住房面积与恩格尔系数之间的关系。

二、人均住房面积与恩格尔系数之间关系的实证分析

对于人均住房面积与恩格尔系数之间的关系，理论上认为此种关系表现为反向变动关系，同时诸方面所对应的的住房支出与包含恩格尔系数的收入函数关系表现为线性关系，但无法确定出住房面积与恩格尔系数的函数关系及住房面积受恩格尔系数的影响程度。为此，本文试图对人均住房面积与恩格尔系数之间的关系进行实证分析，以解决理论分析上遗留下来的问题。

（一）人均住房面积与恩格尔系数之间的线性关系

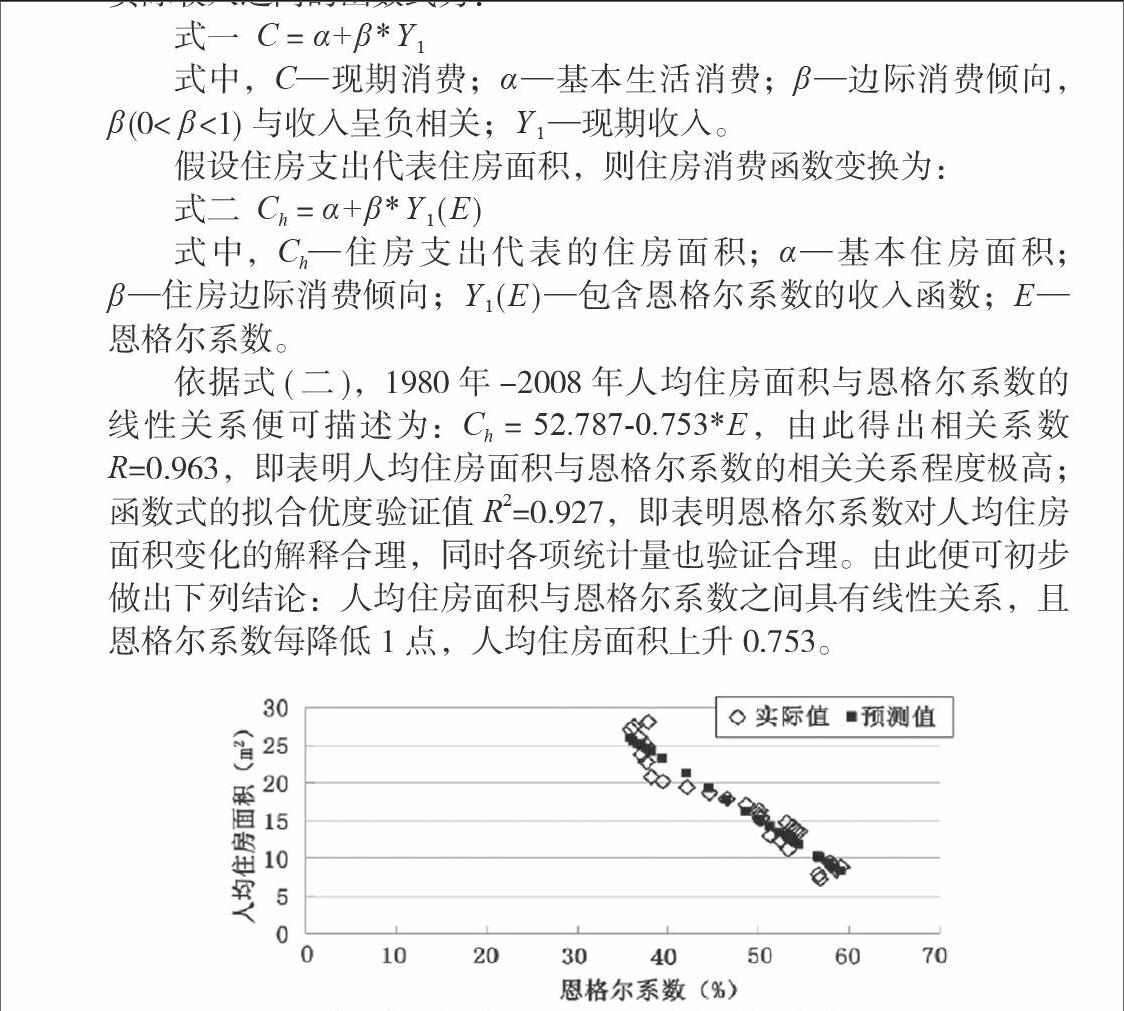
住房是用来满足居民的生存、发展与享受需要的物品，因此当居民收入提高、恩格尔系数下降的同时，住房消费曲线呈上升走向，具体表现为人均住房面积持续增加。图1为1980年-2008年人均住房面积与恩格尔系数之间的线性散点图。如图1所示，实际值由菱形散点表征。依据菱形散点的轨迹，首先假设人均住房面积与恩格尔系数之间具有线性关系，由此创建出因变量为人均住房面积、自变量为恩格尔系数的线性模型，同时采用最小二乘法估计模型。

凯尔斯认为居民绝对收入水平决定着消费支出，而消费支出与实际收入之间的函数式为：

式一 C = α+β*Y1

式中，C—现期消费；α—基本生活消费；β—边际消费倾向，β（0< β<1）与收入呈负相关；Y1—现期收入。

假设住房支出代表住房面积，则住房消费函数变换为：

式二 Ch = α+β*Y1（E）

式中，Ch—住房支出代表的住房面积；α—基本住房面积；β—住房边际消费倾向；Y1（E）—包含恩格尔系数的收入函数；E—恩格尔系数。

依据式（二），1980年-2008年人均住房面积与恩格尔系数的线性关系便可描述为：Ch = 52.787-0.753*E，由此得出相关系数R=0.963，即表明人均住房面积与恩格尔系数的相关关系程度极高；函数式的拟合优度验证值R2=0.927，即表明恩格尔系数对人均住房面积变化的解释合理，同时各项统计量也验证合理。由此便可初步做出下列结论：人均住房面积与恩格尔系数之间具有线性关系，且恩格尔系数每降低1点，人均住房面积上升0.753。

图1 人均住房面积的预测值与实际值比较

（二）人均住房面积与恩格尔系数之间的因果关系

上述分析结果表明，人均住房面积与恩格尔系数之间具有相关性。据此，下文采用Granger因果关系法深入验证人均住房面积与恩格尔系数之间的因果关系。Granger因果关系的检验根本上是对特定变量的滞后变量能够引入其他变量方程中进行验证，即若其他变量会对该变量产生滞后影响，则表明两者之间存在Granger因果关系。Granger因果关系的验证步骤为：

步骤一：根据1980年-2008年人均住房面积与恩格尔系数的时间序列，创建变量VAR模型；

步骤二：对人均住房面积及恩格尔系数进行对数处理，结果显示两者皆为平稳的时间序列；

步骤三：确定VAR模型中变量的滞后阶数，具体依照AIC/SC进行判定，判定值越小越好，即滞后时间等于1时，AIC=-8.47/SC=-8.18，且值最小，则滞后阶数选为1期或1年；

步骤四：采用EViews5.0，创建VAR（1）模型（向量自回归模型），同时验证Granger因果关系。

依据上述步骤得出的验证结果表明，滞后的1-5期中，人均住房面积并非恩格尔系数的原因，符合实际情况；滞后的1/4/5期中，恩格尔系数是人均住房面积的Granger原因，概率为92.33%，此结果符合理论分析的结果，且也与居民的普遍认识相符。

（三）恩格尔系数对人均住房面积的影响水平

根据上述分析内容，下文利用VAR模型对人均住房面积受恩格尔系数的影响程度进行深入分析。对于VAR（1）模型，下列函数式可用来描述人均住房面积：

式三 Loghouse=0.977+0.892*Loghouse（-1）-0.164*LogEn-gel（-1）

根据式（三）可知，上期住房面积会从正面影响到当期住房面积，而上期恩格尔系数会从负面影响到当期住房面积。

脉冲响应函数是用来描述VAR模型中特定内生变量对其他内生变量的影响及当任一误差项变化时或模型受到冲击时系统受遭受的动态影响。下文试图采用脉冲响应函数来描述恩格尔系数对人均住房面积的影响水平。

根据VAR（1）模型，采用广义脉冲法得出变量所对应的广义脉冲响应结果。结果显示，当期恩格尔系数每变动1%，当期人均住房面积便变动-0.15%，而后持续增加至第8期的-2.7%，并最终稳定下来。由此可见，人均住房面积从当期便受到恩格尔系数的反向影响，且此影响值的绝对值随时间的发展而逐渐变大，注意此种影响具有长期性。

三、结语

上文实证分析了人均住房面积与恩格尔系数之间的关系，分析结果表明：人均住房面积与恩格尔系数之间具有线性负相关的关系，即恩格尔系数持续下降的同时，人均住房面积持续增加。总的来讲，人均住房面积与恩格尔系数之间表现出下列变化规律：恩格尔系数低时，家庭富足程度高且人均住房面积大，反之亦然。单单就恩格尔系数来看，我国当前处在富裕阶段，但面对我国特殊的国情，恩格尔系数的反映或许不完全准确，但从改革开放至今，我国居民生活水平明显提高确是不争的事实，而在不久的将来，我国居民定将全面进入富裕阶段。

参考文献：

[1]肖娅.农村居民家庭恩格尔系数与人均居住面积的关系具体测度[J].商，2012，03：120+122.

[2]李翔.基于Eviews软件分析的上海市区人均住房居住面积影响因素研究[J].安阳工学院学报，2013，01：59-62.

[3]刘洋.利率变动与我国恩格尔系数变化的相关性分析[J].河北金融，2014，12：5-8.

[4]周玉科，高锡章，周成虎.全国农村人均住房面积的空间自相关分析[J].测绘与空间地理信息，2014，11：4-6.

[5]张志果，邵益生，徐宗学.基于恩格尔系数与霍夫曼系数的城市需水量预测[J].水利学报，2010，11：1304-1309.