随机激励下动力吸振器参数优化方法

贾安兵, 任传波, 朱　坤, 瞿育文

(山东理工大学交通与车辆工程学院， 山东淄博 255049)



随机激励下动力吸振器参数优化方法

贾安兵, 任传波, 朱坤, 瞿育文

(山东理工大学交通与车辆工程学院， 山东淄博 255049)

摘要：以二自由度振动系统为例，将多个频率下主振动系统的幅频值叠加来构造目标函数，选取合适的最优化方法优化设计动力吸振器的参数，并通过求解、分析振动系统的频域响应和时域响应，比较了设置动力吸振器前后以及取不同频率间隔时动力吸振器的减振效果.结果表明，随着频率间隔的减小，动力吸振器的减振效果变好，但当频率间隔减小到一定程度时，动力吸振器的减振效果变化不再明显.对二自由度振动系统吸振器参数优化设计的思想可以推广到复杂多自由度振动系统中，为随机激励下的动力吸振器参数优化设计提供了一种实用、有效的方法.

关键词：动力吸振器； 参数优化； 随机激励

机械振动会产生噪声以及有损于机械结构的动载荷，影响机器设备的工作性能和寿命，而动力吸振器是机械振动中常用的减振措施之一.李良伟等[1]运用Den Hartog的动力谐调消原理，通过选择适当的固有频率比和阻尼比来实现最大放大系数的最小化；王伟等[2]提出了通过使得幅频特性曲线下的面积最小化来优化动力吸振器参数的方法；侯祥林等[3]编写了一种将放大系数最大值最小化的算法，这种算法以幅频特性曲线下的面积与曲线峰值平方和为目标函数，将一定范围内的固有频率比和阻尼比分为若干个确定值，通过比较得到使放大系数最小的参数；Brown等[4]利用对主系统质量的位移最大值最小化的方法优化动力吸振器参数，其结果对激励频率反应过于敏感； Tigli[5]在此基础上，分别以主振动系统质量的位移、速度、加速度为目标函数，优化动力吸振器参数，分析比较3种方案得出了以主系统质量的速度为目标函数确定的吸振器参数使得吸振效果更佳.总结国内外对吸振器参数优化设计的研究可知[6-8]，对于简谐激励的研究较多，对于随机激励下减振参数优化设计方法的研究较少.本文研究随机激励下动力吸振器参数优化方法，以期使该方法符合实际环境中激励多为随机激励的情况，从而在优化动力吸振器参数的优化设计中更加实用.

1参数优化

1.1振动系统模型

为便于分析吸振器的减振效果，本文将对单自由度振动系统以及设置吸振器后的二自由度振动系统两种振动系统的简化模型进行研究比较.单自由度振动系统以及为其设置吸振器后的模型如图1所示.

根据牛顿第二定律，可建立图1(a)中所示单自由度振动系统模型的运动微分方程，即

(1)

(a)单自由度　　　　　　　(b)设置吸振器后图1　振动系统模型

同理，亦可建立图1(b)中所示二自由度振动系统模型的运动微分方程，即

其中，主振动系统质量m1=1kg，刚度k1=100N/m，阻尼c1=1N·s/m,吸振器质量为m2=0.1kg，刚度k2以及阻尼c2为待优化参数.

1.2构造目标函数

随机激励中包含多个频率，优化设计的减振参数能够在随机激励下使得吸振器达到良好的减振效果，构造目标函数使用的频率应该包括随机激励的主要频率，本文所用目标函数的具体构造过程如下所述.

首先，对式(2)进行傅里叶变换[9]可求得主振动系统的幅频相应函数

(3)

然后，在随机激励主要的频率范围0～25Hz内，等间隔d的取若干频率ω1、ω2、ω3、…，并将与这些频率对应的幅频特性函数|H1(ω1)|、|H1(ω2)|、|H1(ω3)|…叠加来构造目标函数，即

S(k2,c2)=|H1(ω1)|+|H1(ω2)|+|H1(ω3)|+L

(4)

1.3参数优化

式(4)所示的吸振器参数优化设计目标函数自变量为吸振器刚度k2以及阻尼系数c2，使目标函数S(k2,c2)分别对两个自变量求偏导，并令其分别为零，建立方程组

(5)

求解方程组(5)可求得目标函数的极值点，即优化得吸振器的参数k2和c2的值.按照上述步骤在频率范围0～25Hz内分别选取间隔d为5Hz、3Hz、1Hz、0.5Hz、0.1Hz进行参数优化，优化结果见表1.

表1　参数优化结果

2效果分析

2.1随机激励模型

本文参考张永林等[10]对随机路面不平度的总结研究，选用随机正弦叠加的方法来建立随机激励的时域模型.

(6)

将对应于各个小区间的正弦波函数叠加起来,就得到随机激励位移时域模型

(7)

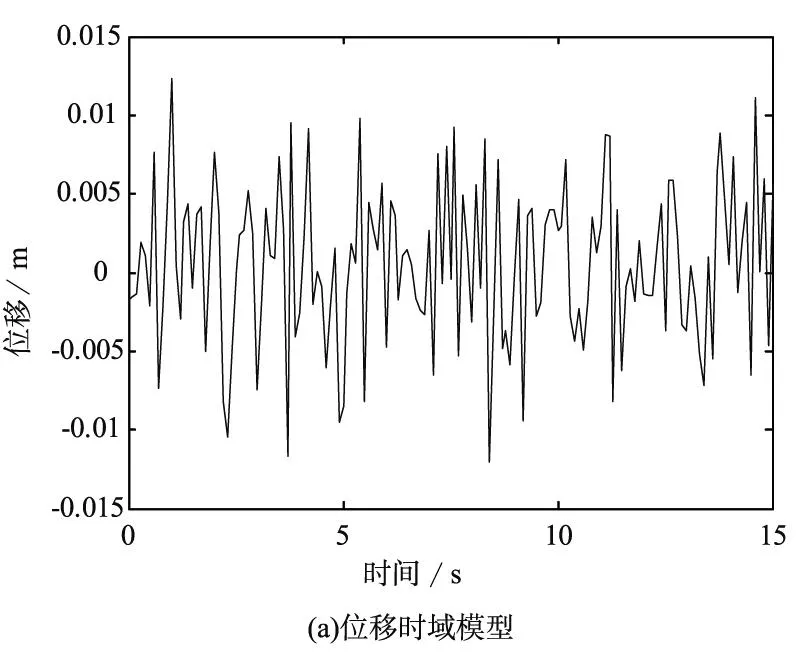
图2 路面随机激励时域模型

2.2时域响应分析

根据建立的随机激励时域模型，在此随机激励下分别将表1各参数值代入式(2)所示的微分方程中求解得对应的位移时域响应及加速度时域响应，如图3中(a)、(b)所示.

图3 时域响应

为便于更加直观地比较不同频率间隔时优化所得参数的减振效果，本文统计了不同频率间隔时优化设计参数后的位移时域响应、加速度时域响应的均方根值(见表2).

表2 位移、加速度均方根值

从图3以及表2中可以看出，随着频率间隔不断变小，吸振器的减振效果越来越好；但是同样可以看出，在频率间隔由1Hz变为0.5Hz，由0.5Hz变为0.1Hz的时候，振动系统的响应虽然在变小，但是变化的幅度不大.在优化设计吸振器的参数时，可以适当地选取频率间隔， 保证既不

会使得优化过程太过繁琐又能得到理想的参数.

3 结束语

本文提供的利用多个频率下主振动系统的频响函数值叠加来构造目标函数，并优化设计吸振器参数的方法，符合振动系统受到的激励多为随机激励的实际情况，优化所得参数使吸振器能在实际的工作环境中大幅减小主系统的振动.同时，本文又以随机激励下二自由度振动系统的参数优化设计为例，验证了这种参数优化方法的可行性，该方法也可应用于多自由度系统参数优化以及车辆减振参数的优化设计中.

参考文献:

[1] 李良伟,赵耀,陆坡,等.减小船舶轴系纵向振动的动力减振器参数优化[J].中国造船,2010(2):139-149.

[2] 王伟,赵庆海,张海燕,等.动力减振器参数优化分析[J].振动与冲击,2006(5):180-184.

[3] 侯祥林,李和玉,刘杰,等.最大值最小化问题的优化算法与多自由度动力减振器参数计算[J].振动与冲击,2008(1):100-106.

[4] Brown B, Singh T. Minimax design of vibration absorbers for linear damped systems [J]. Journal of Sound and Vibration, 2011,330:2 437-2 449.

[5] Tigli O F.Optimum vibration absorber (tuned mass damper) design for linear damped systems subjected to random loads [J]. Journal of Sound and Vibration, 2012,331:3 035-3 050.

[6] 龙岩,史文库,李辉,等.被动吸振器在整车振动控制中的应用[J].振动与噪声控制,2008(5):105-107.

[7] 王琳.动力吸振器的参数设计和动力学分析[D].石家庄:石家庄铁道大学，2012.

[8] Jang S J, Brennan M J, Respighi E,etal. A simple method for choosing the parameters of a two degree-of-freedom tuned vibration absorber[J].Journal of Sound and Vibration, 2012，331:4 658-4 668.

[9] 倪振华.振动力学[M].西安:西安交通大学出版社,1990.

[10] 张永林,钟毅芳.车辆路面不平度输入的随机激励时域模型[J].农业机械学报,2004,35(2):9-12.

(编辑：郝秀清)

One method for optimizing vibration absorber

parameters under random excitation

JIA An-bing, REN Chuan-bo, ZHU Kun, QU Yu-wen

(School of Trasportation and Vehicle Engineering, Shandong University of Technology, Zibo 255049, China)

Abstract:By taking a two-degree-freedom vibration systemfor example, this paper made the summation of response amplitude of the primary vibration systemunder different frequencyas objective function, used the appropriateoptimization method to choose and optimize dynamic vibration absorber parameters; and by workingout and analyzing the frequencydomain and timedomainresponse of vibration system, this paper contrasted the effect ofdifferent frequency intervals. The results showedthatthe smaller the frequency intervals are, the better the effect of the DVA is; but the effectof DVA will not change obviously when the frequency intervals are too small. By optimizing the parameters of a two-degree-freedom vibration systemand analyzing the results, this paper elaborated a thought that can beused to the optimization of parameters of complicatedmulti-degree-freedom vibration system, offereda practical and effective method for optimization of Vibration Absorber parametersunder random excitation.

Key words:dynamic vibration absorber; parametersoptimization; random excitation

中图分类号：O328

文献标志码：A

文章编号：1672-6197(2015)03-0008-03

作者简介：贾安兵，男，jiaanbing@126.com； 通信作者： 任传波，男，chuanboren@sdut.cn

基金项目：国家自然科学基金资助项目(51275280)

收稿日期：2014-09-29