空间自回归模型在新疆R&D溢出效应中的应用

张　静, 张辉国, 胡锡健

(新疆大学数学与系统科学学院， 新疆乌鲁木齐 830046)



空间自回归模型在新疆R&D溢出效应中的应用

张静, 张辉国, 胡锡健

(新疆大学数学与系统科学学院， 新疆乌鲁木齐 830046)

摘要：利用新疆各地州市的工业企业主营业务收入、工业企业科技人员数、工业企业R&D活动中的企业资金作为解释变量，建立了工业企业研究与实验发展经费的空间自回归模型.模型数据分析表明：新疆各地州市工业企业R&D投入存在明显的空间自相关现象，它反映了新疆各地州市工业企业R&D投入存在聚集效应；同一地区的工业企业研发策略表现为显著的替代型互动.研究表明，提高知识产权保护执行力度对有效提高新疆工业企业创新激励具有重要意义.

关键词：空间自回归模型； R&D投入； 替代型互动

空间自相关性的研究已有一段历史并取得了系列研究成果.Gould[1]于1970年首次提出后，有学者相继提出了空间自相关性分析的Moran’s I指数[2]以及空间自回归模[3]等.在Cliff和Ord[2]开拓性工作的基础上建立起来的一个计量经济学分支即空间计量经济学，它主要处理具有空间异方差结构和空间相依特征的经济数据.在计量经济模型中，我们常常遇到面板数据(panel data)和截面数据两种数据，这难免涉及到所研究对象的空间位置和由空间位置而产生的空间关联性.过去人们经常将经济体看作一个整体来分析，但是随着进一步地研究，人们越来越对各个研究对象之间的空间关联性感兴[4].经过大量深入研究，Anselin[3]找到求解无异方差空间自回归模型中所有参数的方法，并给出相关的计算公式和检验统计量，而Lesage[5]在解决有异方差空间自回归模型的参数求解问题时也运用了Bayesian方法.空间计量经济学方法在上述学者的研究和推广下被运用到了许多相关领域.近年来，一些国内学者[6-7]也试图把空间计量方法和一些经济指标的区域特征相结合，通过建立居民收入与城市经济水平的空间自回归模型，李旭颖等[7]分析了江、浙、沪地区居民收入的空间相关性和居民收入对城市经济水平的空间依赖性.作为一种较新的实证工具，空间计量经济学的理论及方法逐渐系统，并成为对经济现象空间特性进行实证研究的有力工具.另外，创新和技术进步是经济发展的主要因素，而技术进步又依赖企业的各种创新活动.虽然大中型工业企业已成为我国创新活动的重要力量，但和发达国家相比，中国的研发投入总体水平还很低，因此研究企业研发投入的策略至关重要.而不同地区的企业之间研发战略可能是相互影响的，可能是互补的，也可能是替代的：一方面，企业可以从竞争对手的创新思维中受到启发，从而促进自身的创新，企业之间竞相开展研发竞赛，增加研发投入以争夺市场份额垄断利润；另一方面，企业可以模仿竞争对手的新技术，当其他企业增加研发投入时，该企业可能选择减少研发甚至不研发.不同地区的研发投入可能存在空间相关性，企业自身因素或行业特征和其“邻居”企业研发投入策略都可能对企业研发投入产生重大影响，即R&D溢出效应.若忽略这一点，则很可能造成模型估计偏误，结论片面甚至毫无意义.工业企业作为我国创新活动的重要力量，其研发投入是否存在策略互动？若存在，是替代型还是互补型？对此问题国外仅有极少数学者对此进行实证检验[8-9].国内相关实证更是几乎空白，宗庆庆[10]首次研究企业研发决策之间的相互影响.本文利用空间自回归模型对新疆各地州市的工业企业的研发投入策略问题进行尝试性探讨.

1空间自回归模型及参数估计方法

1.1空间自回归模型

检验具有空间位置的某要素的观测值与其相邻空间点上的观测值是否有显著的关联性[11]即是空间自相关性分析.空间自相关所统计的内容主要有空间对象的空间位置和空间对象的属性，有许多方法和指标表示空间自相关，最常用的是Moran’sI指数.Moran’sI是用于衡量空间要素的相互关系，其值在-1到1之间.等于零则表明不存在空间相关性，小于零则表明存在负相关，反之为正相关.其计算公式如下：

式中xi和xj分别为i和j所在位置的观测值，wij为权重.而有关空间权重矩阵的选择，目前仍然没有统一的标准，由影响空间交互效应的变量计算得到的权重矩阵和二进制连接矩阵及距离矩[12]是常见的形式.

根据变量之间的空间相关性，Anselin L教授[3]得出一般形式的空间自回归模型，其形式：

(1)

其中y为被解释变量，权重矩阵ω1反映被解释变量本身的空间趋势，权重矩阵ω2反映残差的空间趋势，一般应有0≤ρ<1,0≤λ<1；x为解释变量.此模型可以派生出其它几种模型：

(1) 当ρ=λ=0时， 式(1)为传统的回归模型，记为LR，可以看出模型中，没有空间特性的影响.

(2) 当ρ≠0,β=λ=0时，式(1)为一阶空间自回归模型，记为SAR.此模型与时间序列分析中的一阶自回归模型十分相似，反映了所研究区域的被解释变量如何受到相邻区域被解释变量的影响，即变量在空间上的相关特征.

(3)当ρ≠0,β≠0,λ=0时，式(1)为混合回归与空间自回归模型，记为MSAR.在这个模型中，所研究区域的被解释变量不仅与本区域的解释变量有关，还与相邻区域的被解释变量有关.

(4) 当ρ=0,β≠0,λ=0时，式(1)为空间误差模型，记为SEM，这个模型可以改写为：(In-λω)y=(In-λω)xβ+ε.从中可知所研究区域的被解释变量不仅与本区域的解释变量有关，还与相邻区域的解释变量和被解释变量有关.

1.2参数估计

由于从形式上看各种空间自回归模型中的空间相关性与时间序列问题中的时间方向上的相关十分类似，因此人们希望将用于序列相关和滞后相关的最小二乘估计的性质直接用于空间的情形之中.但是，空间相关的特性是多方向的，因此空间模型分析方法不能直接用时间序列分析方法，如OLS、GLS以及Cochrane-Orcutt迭代算法.而又由于空间自回归模型中的右边含有内生变量，使得最小二乘参数估计通常不具有有效性和无偏性，因此最常用的方法是极大似然估计法、抛面似然法、二阶段最小二乘法以及Bayesian空间统计方法，其中涉及MarkovChainMonteCarlo模拟(简称MCMC)的GibbsSampling技术.

对于截面数据空间自回归模型的一般形式，令A=In-ρω1,B=In-λω2，则模型(1)可表示为

其对数似然函数为：

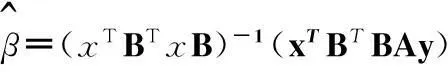
特别地，对MSAR的参数估计可按下面的步骤进行：

(1) 在给定ρ(0)的条件下可利用OLS将L(θ)最后一项最小化，获得最大估计量：记

则

E(I)=tr(ω-x(xTx)-1xTω)/(n-k)

tr(ω-x(xTx)xTω)2+

(tr(ω-x(xTx)-1xTω))2]×

在有空间自相关的情况下，要用伪R2代替传统的R2，它是回归平方和与因变量观测值的离均差平方和比值.在传统回归模型中，它等于R2，但在空间自回归模型中则不等[14].衡量回归模型的参数还有Maximized Log Likelihood(LIK)、Akaike Information Criteria(AIC)、Schwartz Criteria(SC)，LIK值高，AIC、SC值低的空间自回归模型解释能力较强.

2实证分析

本文数据取自新疆乌鲁木齐市、克拉玛依市、吐鲁番地区、哈密地区、昌吉回族自治州、伊犁州直属县(市)、塔城地区、阿勒泰地区、博尔塔拉自治州、巴音郭楞自治州、阿克苏地区、克孜勒苏自治州、喀什地区、和田地区14个地州市2010年的数据(数据来源：2011年新疆统计年鉴).为了研究新疆各地州市的工业企业研发投入的溢出效应，选取工业企业主营业务收入(sr),工业企业科技人员数(ry),工业企业R&D活动中的企业资金(se)作为解释变量，以研究与试验发展经费(rd)为被解释变量.由于区域经济发展的聚集特性，工业企业研究与试验发展经费在空间上还可能存在一定的相关性，而在空间自回归模型中如果存在异方差，参数估计就会变的更为复杂，因此对截面数据取自然对数后不仅可以消除异方差，同时由于模型中的回归系数都成了弹性系数，因此对方程的解释也大有好处.

空间自回归模型为：

其中rd=[rd1,rd2,…，rd14]T，rdi表示第i个地区2010年的工业企业研究与实验发展经费，

sri1表示第i个地区2010年的工业企业主营业务收入，ryi2表示第i个地区2010年的工业企业科技人员数，sei3表示第i个地区2010年的工业企业R&D活动中的企业资金.对于空间加权矩阵我们取ω1=ω2=ω，根据相邻与否构造加权矩阵，在空间加权矩阵中，相邻的地区对应的元素为1，否则为0.用Matlab模拟的各个模型的结果见表1.

表1　Matlab模拟的各模型结果

从上述各类空间自回归模型估计结果可以得出以下结论：

(1)LR模型中工业企业研究与实验发展经费对工业企业R&D活动中的企业资金的弹性系数是0.9955.即工业企业R&D活动中的企业资金增加1万元，研究与实验发展经费就会增加0.9955万元，且工业企业主营业务收入和工业企业科技人员数前的系数都为正，说明其对工业企业R&D投入具有带动作用，是正相关的.

(2)SAR模型估计结果知此模型拟合优度相对于LR模型下降.即影响某地区研究与实验发展经费的主要因素不只是其相邻地区的研究与实验发展经费.

图1　新疆各地州市的研发投入(取对数)

图2　新疆各地州市的研发投入(取对数)局部Moran’s I

(3)MSAR模型和SEM模型的拟合效果都比较好，研究与实验发展经费对工业企业R&D活动中的企业资金的弹性系数分别为0.9955和0.9982，系数都为正，说明企业科技投入对工业企业R&D投入具有带动作用，且从检验结果知新疆各个地区的研究与实验发展经费之间存在空间溢出效应，即新疆各个地区的研究与实验发展经费是负相关，特别地，通过ArcGIS软件做出新疆各地州的研发投入图1及其局部Moran’sI图2可以看出，塔城地区受其相邻地区克拉玛依市、昌吉回族自治州、伊犁州直属县(市)、阿勒泰地区研发投入的溢出效应的影响，博尔塔拉自治州受其相邻地区伊犁州直属县(市)研发投入的溢出效应的影响，克孜勒苏自治州及和田地区受其相邻地区阿克苏地区和喀什地区的研发投入的溢出效应的影响，该地区研发投入为零，即认为研发投入的成本远远大于模仿成本，因此选择模仿其相邻地区的研发技术而自身不研发，其研发策略表现为显著的替代型互动.

技术创新能力是形成企业核心竞争力的关键因素，企业能否进行技术创新、开发新的产品、提供新的服务决定了企业能否在市场上取得领先地位.由于新疆各个地区的研究与实验发展经费是负相关的，所以当某地区领先企业研发时，大多数其他地区企业都尽可能不研发而去模仿其领先地区企业的技术，从而降低了新疆整体的研发水平.因此，政府应对知识产权和技术产权加大保护力度，使企业在模仿其他地区的企业技术的基础上提高自主创新激励和自主研发能力.

3讨论

实证分析表明新疆各地州市的工业企业R&D溢出效应在5%的显著性水平下显著，即新疆各地州市的工业企业R&D投入显著存在空间自相关.研究经济问题时，我们实际遇到的很多经济指标都具有空间聚集效应，并且其截面数据往往存在空间自相关关系，如果我们想更科学，更合理地解释经济现象在空间上的变化特点和规律，就只能建立空间自回归模型并对其进行定量分析.但本文中仍有一些问题值得探讨：

第一，在定义空间邻接矩阵时，多数是以地理上的空间相邻性来度量，实际上R&D溢出并不仅限于相邻地区，也并不完全取决于地理空间距离，不同的相邻关系定义，模型会得到不同的估计结论.

第二，在空间自回归模型中，极大似然估计基于正态分布的假设与实际情况可能并不相符，并且其统计推断是基于渐近性质的，因此必须有足够的样本量才能使估计及推断的结果可靠.在本案例中，如能加大样本量应会有更好的结果.

参考文献:

[1]GouldPR.Isstatisticsinferencethegeographicalnameforawildgoose[J].EconomicGeography,1970,46:439-448.

[2]CliffAD,OrdJK.SpatialProcesses:ModelsandApplications[M].London:Pion,1981.

[3]AnselinL.SpatialEconometrics:MethodsandModels[M].Dordrecht:KluwerAcademicPublishers,1988.

[4]张晓庭.空间统计学简介[J].统计教育，1996(1):35-40.

[5]LesageJP.Bayesianestimationofspatialautoregressivemodels[J].InternationalRegionalScienceReview,1997,20(1-2):113-129.

[6]邹艳芬，陆宇海.基于空间自回归模型的中国能源利用率区域特征分析[J].统计研究，2005(10):67-71.

[7]李旭颖，陈宏民.居民收入与城市经济水平的空间自回归模型[J].系统工程理论方法应用，2005,14(5)：395-399.

[8]Cockburni,HendersonR.Racingtoinvest?Thedynamicsofcompetitioninethicaldrugdiscovery[J].JournalofEconomicsandManagementStrategy,1994,3(3):481-519.

[9]ZizzoD.Racingwithuncertainty:Apatentraceexperiment[J].InternationalJournalofIndustrialOrganization,2002,20(6):877-902.

[10]宗庆庆.中国工业企业R&D投入的策略互动行为研究[J].财经研究，2013,39(10):46-59.

[11]DavidMartin.Anassessmentofsurfaceandzonalmodelsofpopulation[J].InternationalJournalofGeographicInformationSystems,1996,10(8)：973-989.

[12]LegendreP,LegendreL.NumericalEcology:DevelopmentsinEnvironmentalModelling20[M].Amsterdam:Elsevier,1998.

[13]李序颖，顾兰.空间自回归模型及其估计[J].统计研究，2004(6)：48-51.

[14]AnselinL.Underthehood:Issuesinthespecificationandinterpretationofspatialregressionmodels[J].AgriculturalEconomics,2002,27(3):247-267.

(编辑：姚佳良)

The application of spatial autoregressive model in Xinjiang R&D spillover effect

ZHANG Jing, ZHANG Hui-guo, HU Xi-jian

(College of Mathematics and System Science, Xinjiang University, Urumqi 830046， China)

Abstract:If the industrial enterprise's main business income of all the cities in Xinjiang, the number of persons in science and technologyof industrial enterpriseand the enterprise capitalof industrial enterprise R&D in activitiesare used as explanatory variables, then spatial autoregressive modelof research and experimental development funds in the industrial enterprise can be established. Model data analysis shows that there is obvious autocorrelation phenomenonin industrial enterprise R&Dinvestment in all the cities of Xinjiang,and it reflects the gathered effect of industrial enterprise R&Dinvestment there.The R&D strategy of industrial enterprisein the same area is characterized by significant alternative interaction.The reasearch of this articleshows that improvethe protection of intellectual property rightsis important to improve the innovation motivationof industrial enterprisein Xinjiang.

Key words:spatial autoregressive model； R&D investment； alternative interaction

中图分类号：O211.9

文献标志码：A

文章编号：1672-6197(2015)03-0015-05

作者简介：张静，女， 81361424@qq.com; 通信作者： 胡锡健，男，xijianhu@126.com

基金项目：国家自然科学基金资助项目(41261087)； 教育部青年基金资助项目(12XJJC910001)； 新疆文科基地重大项目基金(0601920)

收稿日期：2014-09-10