固定点法GBSAR大气扰动误差改正方法研究

汪学琴，岳建平，邱志伟

(河海大学地球科学与工程学院，江苏 南京 210098)

WANGXueqin,YUEJianping,QIUZhiwei

固定点法GBSAR大气扰动误差改正方法研究

汪学琴，岳建平，邱志伟

(河海大学地球科学与工程学院，江苏 南京 210098)

ResearchofAtmosphericDisturbanceCorrectioninGround-basedSARbyGroundControlPoints

WANGXueqin,YUEJianping,QIUZhiwei

摘要：大气扰动是影响GBSAR观测精度的主要因素，基于固定点法的误差改正研究具有实际意义。本文基于GBSAR的IBIS-L系统获取监测区域实时位移信息，利用不同分布的固定点对位移进行了改正，得到目标点实际位移量。将改正后位移量与传统正垂线数据进行了对比分析。试验结果表明，固定点法可剔除大部分大气扰动影响，改正效果显著，且不同点位的固定点改正效果存在差异。

引文格式： 汪学琴，岳建平，邱志伟. 固定点法GBSAR大气扰动误差改正方法研究[J].测绘通报，2015(9)：24-27.DOI:10.13474/j.cnki.11-2246.2015.0270

关键词：GBSAR；大气扰动；误差改正；固定点；正垂线法

中图分类号：P237

文献标识码：B

文章编号：0494-0911(2015)09-0024-04

收稿日期：2014-07-28

基金项目：水能资源利用关键技术湖南省重点实验室开放研究基金(PKLHD201311)；国家自然科学基金(41174002)

作者简介：汪学琴(1991—)，女，硕士生，主要从事大地测量与测量工程方面的研究工作。E-mail：wxqstay@163.com

一、引言

地基合成孔径雷达(ground-basedsyntheticapertureradar，GBSAR)技术是一种基于微波主动探测成像的雷达观测技术，由星载合成孔径雷达干涉技术发展而来。该技术综合运用合成孔径技术与步进频率技术[1-2]，克服了星载SAR技术在时空失相干和时空分辨率方面的不足，并且可获取测区的二维影像[3]。GBSAR技术沿袭了InSAR技术的全天时、全天候、局域性、高精度、定点连续监测、灵活且可操作等优势，在变形监测与灾害预警等方面的应用越来越受到关注[4]。IBIS(imagebyinterferometricsurvey)遥测系统是由意大利IDS公司与佛洛伦萨大学基于GBSAR相关理论基础上联合研制的，能够对目标物的变形值提供高精度监测[4-5]。GBSAR差分干涉测量的精度较高,在较好的观测条件下，视线向测量精度可达亚毫米级，但实际测量中，因受到多方面因素的影响，精度有所降低[6-7]。影响干涉测量精度的因素有：系统频率不稳定、大气扰动、目标散射特性变化和噪声等，其中大气扰动是主要因素且其影响可达厘米级。为保证测量的精度，必须有效改正大气扰动的影响。

本文以IBIS-L系统为试验平台，以试验坝体上布设的监测目标点为研究对象，在试验区域稳定位置选取固定点(groundcontrolpoints，GCP),利用固定点法改正目标点位移数据，分析该方法对大气扰动误差的改正效果。

二、固定点法

由于大气环境在时间和空间上的不均匀性与实时性，使得大气扰动的影响较为复杂。尤其是当测区范围大、观测环境不稳定时，大气影响的干扰更为复杂。当研究区域范围较小、观测环境较稳定时，可假设大气环境影响均匀。固定点法以此假设为前提，在测区内选择稳定点作为GCP，对大气干扰量进行反演，利用差分原理改正测区内其他监测点的大气干扰量[8]。

假设φatm(r,t)为大气扰动相位,大气扰动值用函数h(r,t)表示,该函数的自变量为视线方向距离r和观测时间t,可将目标点的干涉相位表示为[9]

φ(r,t)=φdis(r,t)+φatm(r,t)=φdis(r,t)+

K·h(r,h)·r

(1)

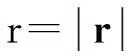
1. 一阶改正模型

大气扰动值函数可近似认为是仅与时间有关的常数h,那么，监测目标点的干涉相位函数简化为

φ(r,t)=φdis(r,t)+K·h·r

(2)

选取的GCP位于稳定区域，变形相位为零，其视线方向距离为r0。由该GCP的差分相位φ0=(r0,t)计算出

K·h=φ0(r0,t)/r0

(3)

将式(3)带入式(1)，可得到任何目标点改正后的差分相位的计算公式，即

φcorr(r,t)=φ(r,t)-[φ0(r0,t)/r0]·r

(4)

式中，φcorr(r,t)为目标点改正后的差分相位，可由此计算得距离值。

一阶改正模型适用于气象条件变化不大的较小区域。

2. 二阶改正模型

大气扰动函数可表示成距离的函数

h(r,t)=A(t)+B(t)·r

(5)

式中，A(t)和B(t)为与时间相关的常数。目标点的干涉相位可表示为

φ(r,t)=φdis(r,t)+K·[A(t)+B(t)·r]·r=

φdis(r,t)+a·r+b·r2

(6)

式中，a和b为随时间变化的系数。

通过两个已知的固定点R1和R2的差分相位可求得a和b的估值

φ1(R1)=a·r(R1)+b·r2(R2)

(7)

φ2(R2)=a·r(R1)+b·r2(R2)

(8)

(9)

最后，可由改正后的差分相位计算目标的位移值[10]

Δr=c·φcorr(r,t)/4πfc

(10)

二阶改正模型可用于气象条件变化明显的较大区域。

三、试验分析

1. 试验介绍

选取隔河岩大坝为试验场地，其位于清江下游湖北省长阳土家族自治县境内。此大坝为上部重力坝、下部重力拱坝的组合坝型[11]，坝顶长653.8m，坝顶高程206m，坝体高程150m以下设置为重力拱坝。雷达视线横跨坝体周围水面，隔河进行观测。试验观测时间为2013年7月31日11：47至8月1日4：00。以IBIS-L遥测系统为平台进行试验研究。本次试验为小范围观测，利用固定点法校正大气扰动时，采用一阶改正模型。在坝体外稳定区域架设GBSAR设备，约5min采样一次，共获取187组数据。在隔河岩大坝坝体上选取广泛分布的10个观测目标点(pix1至pix10)，点位分布如图1所示，分别对其位移值进行统计分析。

2.GCP点位分布影响

固定点法基本原理为：在试验区域选取GCP，作为改正坝体各pix大气扰动值的依据。在隔河岩大坝区域内选取2个GCP，其中GCP1位于坝基处，GCP2位于坝体之上，具体点位如图1所示。坝基为稳定区域，试验中可认为坝基处GCP1始终为稳定点，位移值主要由大气扰动引起。各个目标点改正前的位移值主要由各自自身位移和大气扰动误差共同构成。忽略仪器频率影响后，试验中位于坝体上的GCP2观测位移量主要来自坝体自身位移和大气扰动。GCP2的点位分布靠近隔河岩大坝正中央的15#坝段，以试验起始时刻的径向位移值为参考，利用正垂线法实测坝体高程169m处的相对径向位移值。从7月31日11:50至8月1日4:00,每10min监测一次，共98组数据，垂线法所得形变信息如图2所示。将其归化到视线向后可对GCP2的位移值进行初步改正。经过初步改正后，GCP2的位移值可视为大气扰动误差。由GCP1和GCP2的大气扰动误差分别得到各自的改正参数a，即一阶模型的改正系数，由此可得每个目标点的2组位移改正值，分别对10个目标点进行改正，所得结果如图3、图4、图5所示。

图1　点位分布图

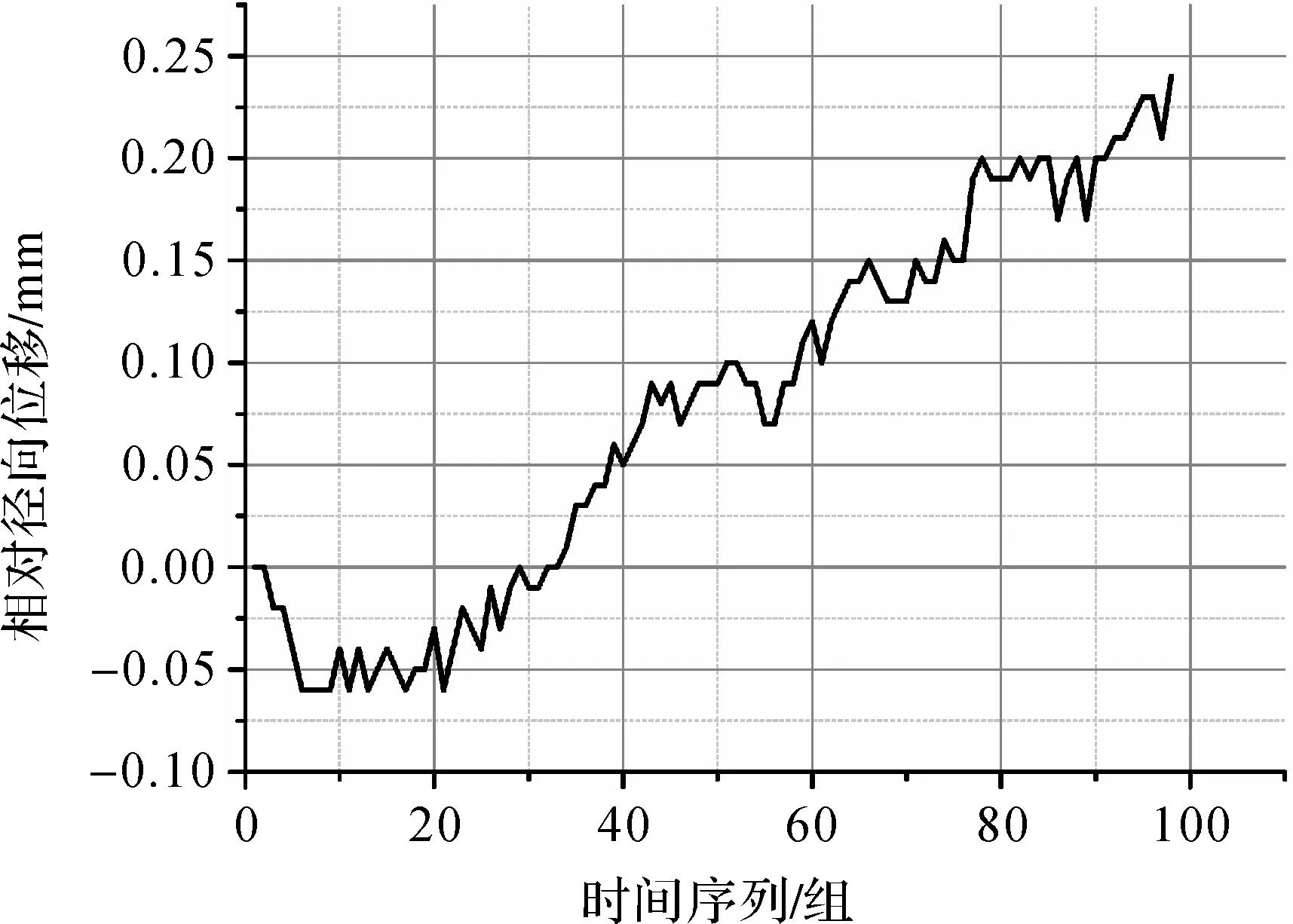
图2　15#坝段169 m处正垂线观测值

由图3可知，改正前各个目标点的视线向位移值波动可达厘米级，个别目标点位移值最大可达-15mm，且在中间段发生剧烈跳动，在后半段变化较平稳。可见，大气扰动的影响较大，不可忽略。10个目标点虽然分布位置存在差异，但位移值的总体变化趋势基本一致。对比图4、图5可发现，在本试验的小区域范围内，坝基处GCP1和坝体上GCP2的改正效果基本相同。在选取坝基处GCP1、坝体上GCP2对目标点进行改正后，各个目标点的视线向位移值波动均明显减小，位移总体分布在±2mm。改正后变化总体趋势与改正前相似，在中间时间段波动明显，但最终趋于平稳。可见，固定点法可以改正大部分大气扰动影响，且一次改正模型可以较好满足小区域改正需求。

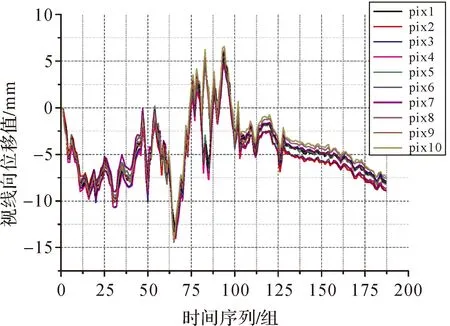
图3　改正前视线向位移值

图5　GCP2改正后视线向位移值

3. 改正效果分析

试验数据表明，位于坝体上的10个目标点改正前后的总体变化趋势相仿。为具体分析改正效果，现选图1中位于坝体正中部坝段的pix5为研究目标点。该点位于坝体正中坝段靠近坝顶处，其位置与正垂线法观测的高程169m处目标点位置大体相同，因此将其视线向位移值归化到垂线法的相对径向后，其值与垂线法测得的形变数据具有可比性。

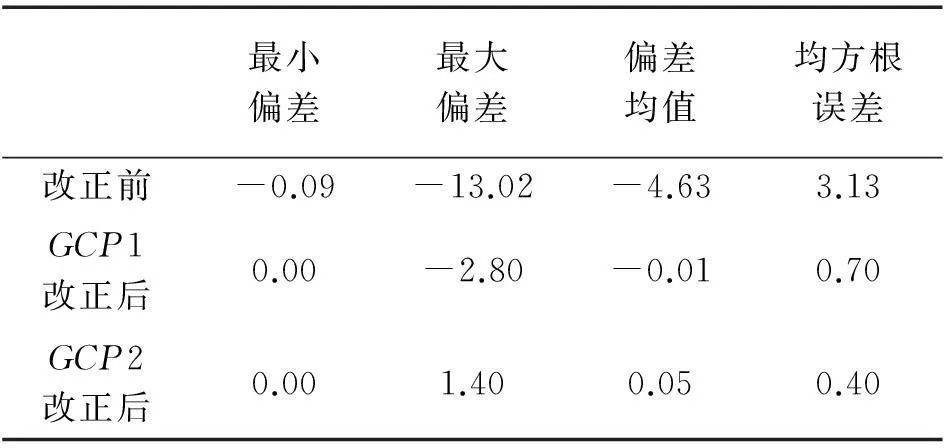
正垂线法为较传统的大坝变形监测方法，能够为气象补偿法改正效果的分析提供可靠依据。对正垂线法所得98组数据进行线性插值，使其与GBSAR数据具有统一时间间隔。根据坝基处固定点GCP1和坝体固定点GCP2的改正系数，对pix5的GBSAR数据分别进行改正。将固定点法改正前、GCP1改正后、GCP2改正后的相对径向位移值分别与同时刻正垂线法所测相对径向位移值进行差值，所得对比结果如图6、表1所示。由图6和表1中3个位移差值可看出：固定点法改正前位移值与垂线法位移值的差值达厘米级，最大可达13mm，最小约0.10mm，经固定点法改正后，差值明显减小。经坝基处GCP1改正后差值绝对值控制在2.80mm之内,偏差均值为-0.01mm。经坝体上GCP2改正后差值绝对值控制在1.40mm之内,偏差均值为0.05mm。利用GCP1和GCP2改正后的差值总体趋势一致，总体相差不超过±1.50mm。由此可知，对于较小范围，一阶固定点法可有效改正大气扰动误差，且改正效果明显。GCP1、GCP2改正后差值的均方根误差分别为0.70mm、0.40mm。当测区较小且坝体较稳定时，在坝基和坝体上选取固定点进行改正，均可有效改正大气扰动误差，且改正效果相差较小。选取坝体上的点作为固定点改正效果更为理想。

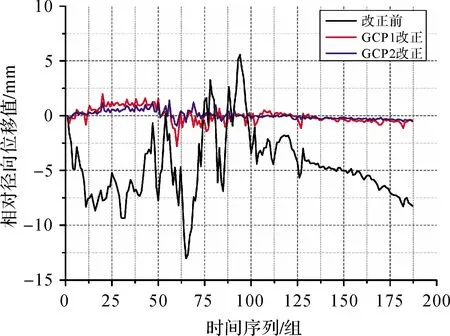
图6　改正前后位移值与正垂线位移值差值对比

mm

四、结束语

GBSAR技术的监测精度较高，可以满足实际工程需要。但是，该技术受环境影响较大，尤其是大气扰动的干扰，对观测结果影响明显。为了将该技术广泛而精确地应用于变形监测，大气扰动的改正研究成为提高观测精度的关键。本文针对IBIS-L系统获取的数据，选取不同分布的GCP，利用固定点法对试验区域的坝体目标点进行气象改正，并与垂线数据进行对比分析。结果表明，在较小区域内，一阶固定点法有效剔除了大部分气象扰动影响，提高了位移测量的精度。

参考文献：

[1]黄其欢,张理想. 基于GBInSAR技术的微变形监测系统及其在大坝变形监测中的应用[J].水利水电科技进展, 2011,31(3):84-87.

[2]ROSENPA,HENSLEYS,JOUGHINIR,etal.SyntheticApertureRadarInterferometry[J].ProceedingsoftheIEEE, 2000, 88 (3):333-382.

[3]杨红磊,彭军还,崔洪曜.GB-InSAR监测大型露天矿边坡形变[J].地球物理学进展,2012,27(4):1804-1811.

[4]RODRIGUEZE,MARTINJM.TheoryandDesignofInterferometricSyntheticApertureRadars[J].RadarandSignalProcessing, 1992, 13(9): 147-59.

[5]岳建平，方露，黎昵.用时间序列分析法进行建筑物沉降观测数据处理的研究[J].测绘通报，2007(7)：1-4.

[6]NOFERINIL,PIERACCINIM,MECATTID,etal.UsingGB-SARTechniquetoMonitorSlowMovingLandslide[J].EngineeringGeology, 2007,95(3): 88-98.

[7]周校,王鹏,邢诚. 基于GB-SAR的建筑物微变形测量研究[J].测绘地理信息,2012,37(5): 40-43.

[8]张祥,陆必应,宋千. 地基SAR差分干涉测量大气扰动误差校正[J].雷达科学与技术，2011,9(6): 502- 506,512.

[9]LUZIG,PIERACCINIM,MECATTID,etal.MonitoringofanAlpineGlacierbyMeansofGround-basedSARInterferometry[J].IEEEGeoscienceandRemoteSensingLetters, 2007,4(3): 495-499.

[10]张捍卫,丁安民,雷伟伟.空间大地测量学中的大气折射理论[M].北京：测绘出版社, 2011.

[11]刘德军,赵全麟,裴灼炎. 隔河岩大坝变形监测资料分析[J].人民长江，2000,31(6):39-41.