基于多标尺联合标定的经纬仪测量系统精度分析
肖华杰 范百兴 西 勤 潘廷耀 杨 凡 杨在华2
(1.信息工程大学 地理空间信息学院,河南 郑州450001;2.北京卫星环境工程研究所,北京100094)
1 引言
经纬仪测量系统由两台及两台以上的高精度电子经纬仪与计算机联机构成,根据空间前方交会原理获取空间点的三维坐标,系统的尺寸通过对基准尺的测量来确定。经纬仪测量系统可实现高精度、无接触测量。经纬仪测量系统一般采用0.5″的电子经纬仪,典型的工作范围为几米至几十米,点位精度为±(0.05~0.1)mm。经纬仪测量系统的优点是测量范围大,对环境的要求不高,是光学、非接触式的测量系统;缺点是人工照准目标,因而测量速度慢、自动化程度低。本文试验将在MetroIn工业测量软件下完成,对经纬仪测量精度的提高进行一些探索。
2 经纬仪测量系统分析
2.1 经纬仪空间前方交会原理
传统经纬仪建站采用两台经纬仪经过互瞄测量(相对定向)、基准尺测量(绝对定向)等步骤后,建立空间测量坐标系,如图1所示。
传统建站方法的测量步骤如下:首先,A、B两台经纬仪互相对瞄来进行相对定向,测得起始方向值(γAB,αAB)和(γBA,αBA)。然后 A、B分别对基准尺L的两端P1、P2进行观测,得到方向值(γAPi,αAPi)和(γBPi,αBPi),其中(i=1,2)。
此时,整个定向测量控制网中,存在如下的观测误差方程:
(1)由A、B两台电子经纬仪互瞄测量的水平角和垂直角等四个观测值得到的4个观测方程;
(2)测量基准尺的两个端点的水平和垂直角度值所得到的8个观测方程;
(3)基准尺的长度L可以视为已知长度基准,从误差方程的角度讲,基准尺长度即可作为一个约束条件;
根据上述观测值及长度约束条件,即可得到两台经纬仪建站时的误差方程组,进一步可以解算得到以下未知参数:
(a)A、B两台经纬仪的测站参数 (X01,Y01,Z01,Rx1,Ry1,Rz1)、(X02,Y02,Z02,Rx2,Ry2,Rz2);
(b)基 准 尺 端 点 P1、P2 的 (X1,Y1,Z1)、(X2,Y2,Z2);
这样,我们就建立好了测量坐标系(以经纬仪A的中心为坐标原点,A、B的连线在在水平面内的投影为X轴,经过A的中线的垂线的反方向为Z轴),可以对空间点进行交会测量,进而得到测量点的坐标。
目前,经纬仪交会测量系统均采用独立线状约束条件,最常用的是0.9m~1.5m的碳纤维或殷钢基准尺,基准尺的长度经过更高精度的仪器进行标定,以双频激光干涉仪配合光电瞄准仪测量基准尺为例,其标测距称精度优于±10μm。
因此,基准尺长度、交会距离和交会角度、基准尺的位置和姿态(基准尺与测站基线的关系)等因素,都会影响系统的建站精度。
2.2 传统经纬仪建站测量的缺点
通过对传统经纬仪建站方法的分析,可以发现该方法存在如下缺点:
(1)多余观测数较少
整个建站控制网中,未知参数的个数为12,而总观测误差方程个数为12,顾及到基准尺的长度约束所产生的一个误差方程,多余观测个数只有1个。从误差分析的角度讲,多余观测数较少时,单位权中误差增大,整个系统的重复测量精度会降低。
(2)系统建站无法检测系统粗差
整个系统中由于多余观测较少,且只有一个基准尺的长度作为整个系统的长度基准,因此系统对粗差的检核能力很差,当系统存在粗大误差时,无法及时的进行系统自我检核。
(3)受基准尺位置和姿态的影响较大,点位精度分布不均匀
经纬仪在测量空间三维坐标时,由于受空间角度前方交会测量原理的限制,点位精度在空间分布不均匀,以点位误差在XOY面上点位误差分布为例,其误差椭圆分布如图2所示。
从图2中可以看出,点位误差随着距离的增加而增加,近似呈现线性变化关系,此外,点位误差受交会角度的影响也很显著。要提高点位测量的精度,改善点位误差的空间分布特性,需要在空间不同的位置和姿态增加约束条件。
基准尺的不同放置位置和姿态,对系统整体定向的精度影响不同,因此,在同一个定向系统下,对于同一根基准尺,如果多次放置不同的位置和姿态,则可以极大地改善系统的定向精度。
从另一方面讲,对基准尺进行测量时,基准尺单点照准精度约在±5~±7μm,在观测条件较差时,照准精度还会低一些。实际测量中,用检定的长度进行解算时,由于照准误差的存在,实际上相当于基准尺长度已发生了变化,因此会影响到整个网的尺度基准。但由于照准误差是随机性的,所以,通过多个位置测量基准尺,可以减弱照准误差。
3 多标尺联合标定建站测量
当我们测量的空间较大时,我们就在空间放置较多的基准尺,均匀分布在待测的空间内,将所有的基准尺都参与坐标系解算,这样就会有更多的约束条件,可以在全方位测量空间内较好地控制的测量误差,改善测量误差的空间分布
对整个空间的整体测量精度来说将会得到一定的提高。
具体试验如图3所示:
(1)A、B两台TM5100A电子经纬仪进行精确互瞄;
(2)经纬仪测量L1-L9位置的全部碳纤维基准尺基准尺;
(3)系统定向解算(所有标尺统一参与坐标系解算),得到A、B两台经纬仪的测站参数;
(4)依次测量L1-L9位置的基准尺的两个端点,得到每个位置两个端点的三维坐标值(x1,y1,z1)和(x2,y2,z2);
这样我们就得到了多个基准尺联合参与定向解算时,这9个点位的测量精度。
4 试验与分析
本实验是为了验证在测量空间较大时,用经纬仪测量系统建站时,分别选用不同位置的约束点和标尺、多位置的约束点和标尺联合解算对经纬仪布站及测量精度的影响。示,在相距约3米的AB两点架设TM5100经纬仪,直线AB距墙面约4米。测量区域在墙面上的约8×2的范围内进行,分别设定9个基准尺位置,这九个位置的摆放要尽量均匀,以便得到不同区域内的测量精度。
因为在经纬仪测量系统中,基准尺长度、交会距离和交会角度、基准尺的位置和姿态(基准尺与测站基线的关系)等因素,都会影响系统的建站精度。因此,我们将给定多个基准尺的位置,尽可能的铺满整个平面,但又受到客观因素的限制,我们选择了具有代表性的9个位置。当然,经纬仪测量精度还受其他精度的影响,如人眼照准误差、仪器系统误差、指标差、环境变化引起的误差等,但这些误差都能通过一定的测量方法和手段来削弱,如正倒镜观测、多次观测取平均、仪器增加配种等方法。
5 总结
5.1 实验数据及比较结果
下表是3种测量方式在9个位置的标尺长度测量偏差。
单一位置标尺:是在L5位置测量一次基准尺,只用L5位置的基准尺参与定向解算,解算完之后进行单点坐标测量。
我们选择在一个比较稳定的空间内如图4所
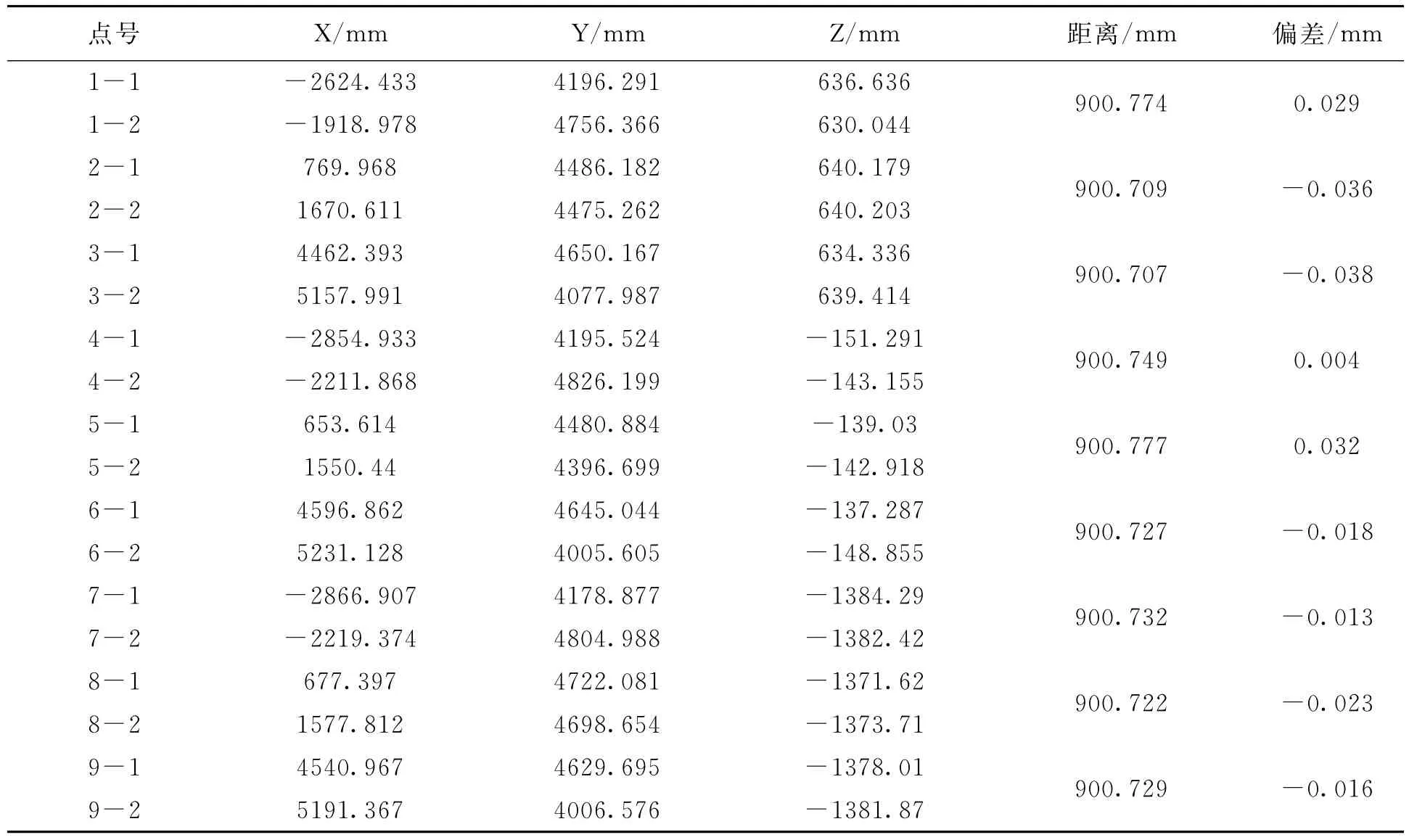
表1 单一位置标尺测量数据
特征位置标尺:是在L1位置测量一次基准尺,只用L1位置的基准尺参与定向解算,解算完之后只对L1位置的基准尺进行单点坐标测量。依次类推,用L2基准尺定向解算,测L2位置处基准尺。
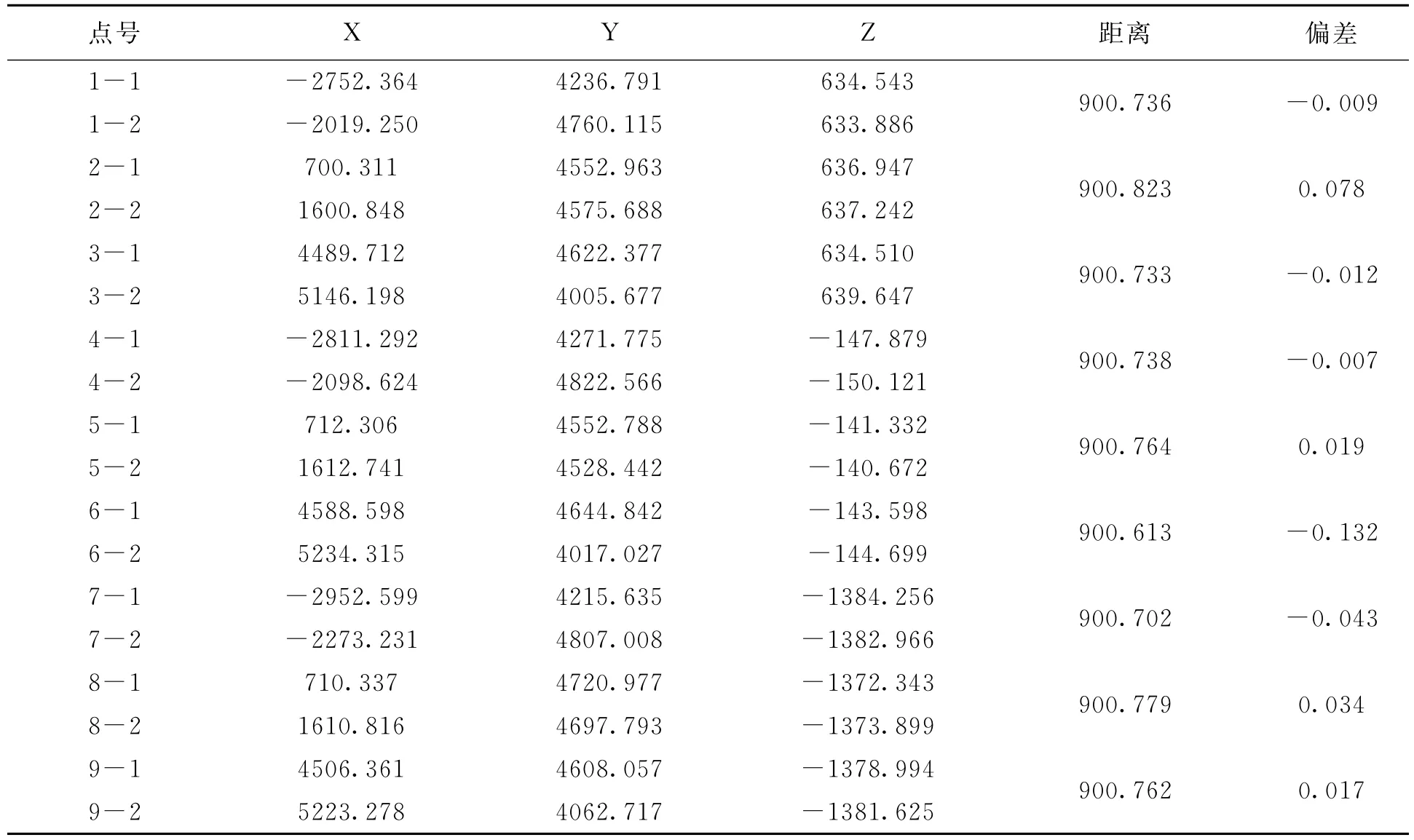
表2 特征位置标尺测量数据
多标尺联合测量:是将这九个位置的基准尺 全部参与定向解算,然后进行单点坐标测量。
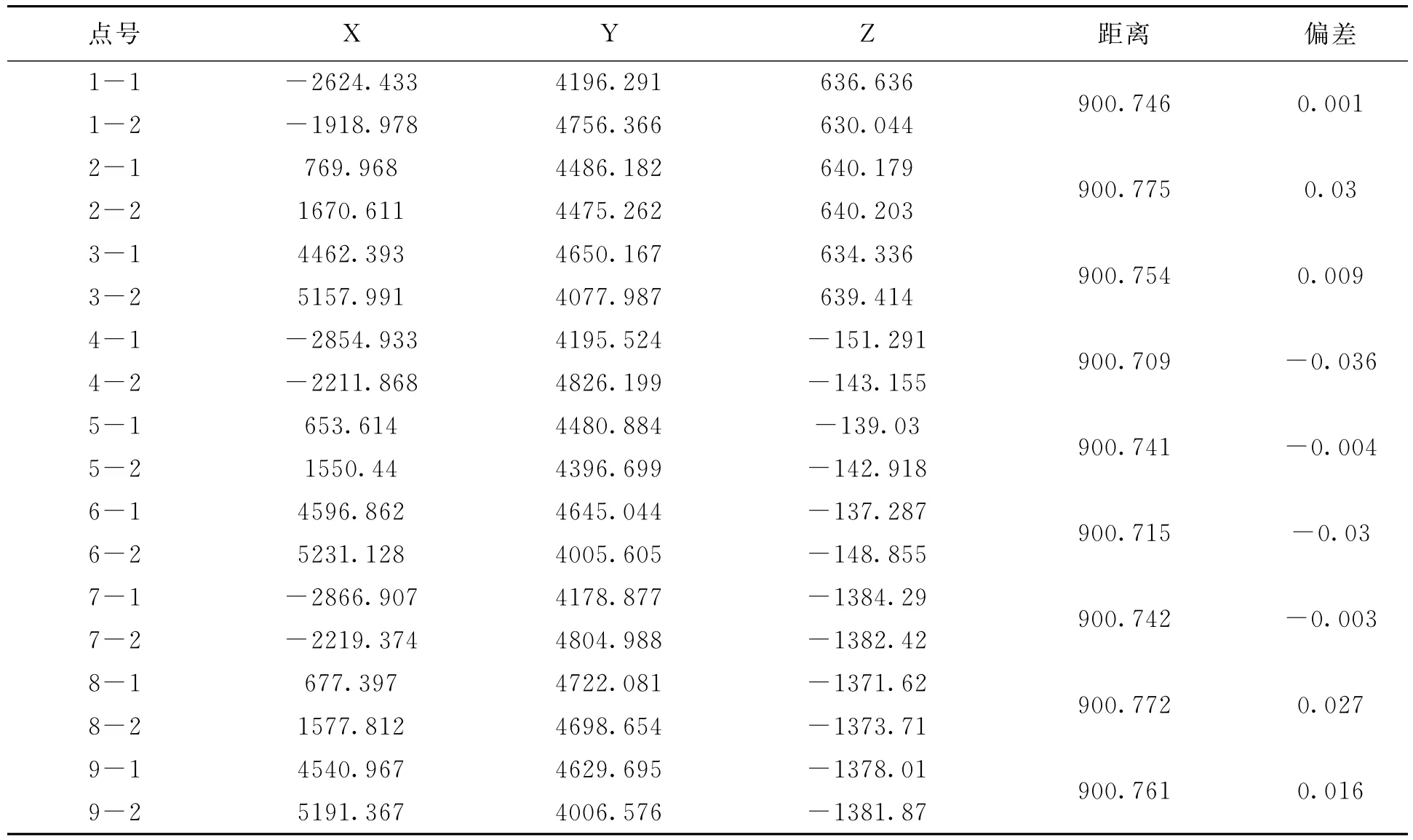
表3 多标尺测量数据
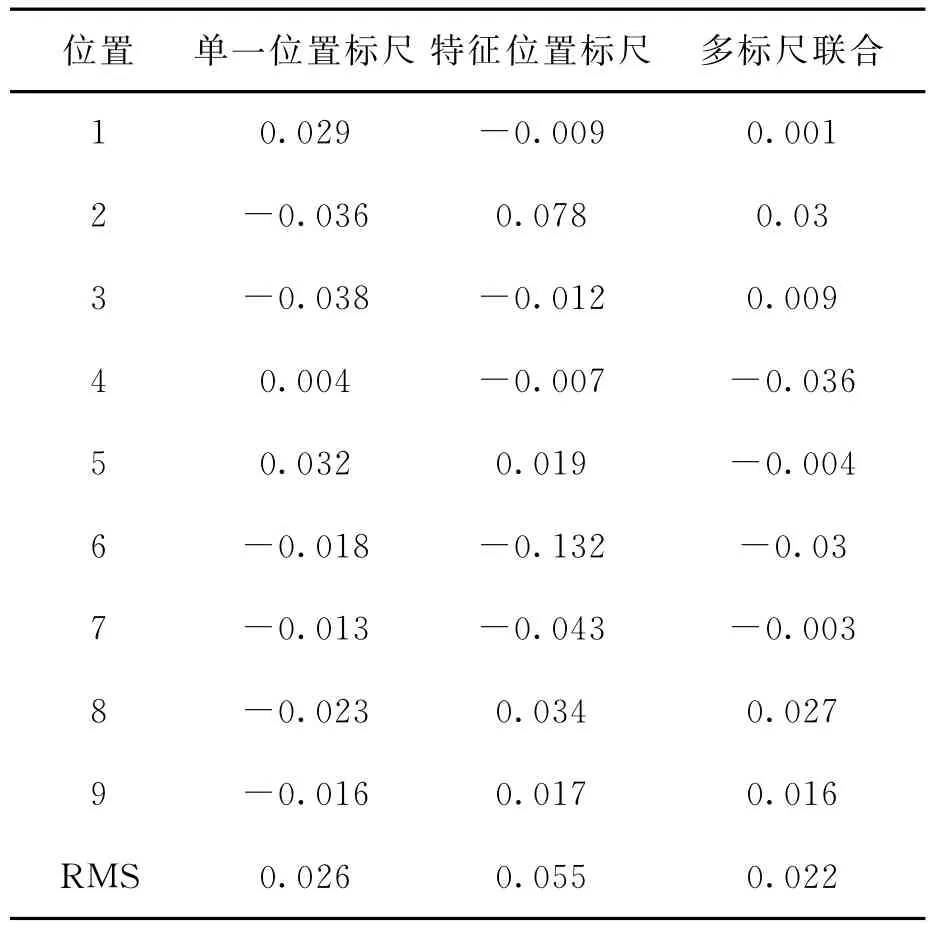
表4 三种方法比较结果
5.2 小结
综合以上结果,大致可以看出:
(1)只在特征位置放置标尺,并不能提高特征位置的测量精度,这依然取决于基准尺的测量精度。
(2)在图形位置最好、交会精度较高的位置放置基准尺,更有可能提高基准尺的测量精度,从而提高整网的测量精度。
(3)当测量范围较大时,采用多标尺联合标定的测量方法,对整体测量精度有提高。在经纬仪测量的全方位空间内,增加多个位置的基准尺,可以极大地改善系统定向的精度,系统的可靠性也更高。

