Zygmund型函数类的光滑性

高丹丹,李俊福,肖建斌

(杭州电子科技大学理学院，浙江杭州310018)



Zygmund型函数类的光滑性

高丹丹,李俊福,肖建斌

(杭州电子科技大学理学院，浙江杭州310018)

摘要：Hardy G.H.和Littlewood J.E.对Lipschitz函数类进行了刻画，获得了函数是Lipschitz函数类的充分必要条件，Zygmund A.定义了类似Lipschitz函数族的函数类，并给出了充分必要条件。在这两类函数类的基础上给出Zygmund型函数类的定义，并获得了函数为Zygmund型函数类的充分必要条件。

关键词：函数类；Zygmund定理；Hardy-Littlewood定理；二次方差

0引言

1预备知识

1.1　基本定义及符号

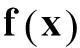
HardyG.H.,LittlewoodJ.E.和ZygmundA.分别定义下面3种函数类，并对其进行了刻画。

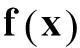
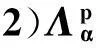
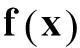
1.2　相关定理

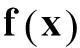
同时ZygmundA.也获得单位圆盘内解析函数与其边界函数具有Λ*性的充分必要条件：

2主要定理

证明1)充分性

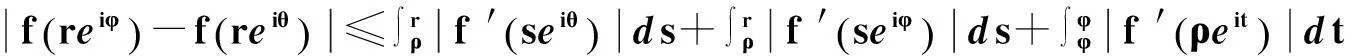
(1)

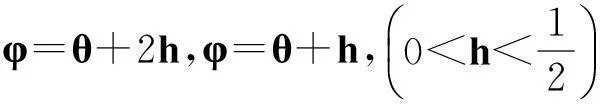
(2)

(3)

2)必要性

综合以上证明，得出定理4的正确性。

3结束语

本文给出了一种新的Zygmund型函数类，并且研究获得了函数为该Zygmund型函数类的充分必要条件，本文的研究对于研究Zygmund型函数类光滑性等性质有着重要的意义。

参考文献

[1]Duren P L.THEORY OFHp SPACE[M].New York:Academic press,1970:33-51,71-90.

[2]Rudin W.实分析与复分析(英文版)[M].北京:机械工业出版社,2006:50-54.

[3]任福尧.一个Zygmund定理的推广及应用[J].数学研究与评论,1988,(3):391-400.

[4]朱来义.Zygmund定理的一点注记[J].北京大学学报(自然科学版),1991,27(3):281-285.

[5]韦金生,朱来义.一致区域和Zygmund性质[J].数学杂志,1995,15(2):215-218.

[6]王朝祥,黄心中.闭区间上Zygmund函数的延拓定理[J].华侨大学学报(自然科学版),2006,27(2):119-122.

[7]宋金荣.关于Zygmund函数诱导的一个积分算子[D].苏州:苏州大学,2013:11-13.

[8]刘永民,郭健.Hardy空间到Zygmund型空间的Riemann-Stieltjes算子[J].数学学报,2014,57(4):693-708.

Smooth of the Zygmund Function Class

Gao Dandan，Li Junfu，Xiao Jianbin

(SchoolofScience，HangzhouDianziUniversity，HangzhouZhejiang310018，China)

Abstract：Hardy and Littlewood described the Lipschitz function and obtained a function is a sufficient and necessary condition for the Lipschitz class.The definition of Zygmund is similar to the Lipschitz class of functions，and gives a necessary and sufficient condition.In this paper，we give the definition of Zygmund type function on the basis of these two kinds of functions，and obtain a necessary and sufficient condition for Zygmund type functions.

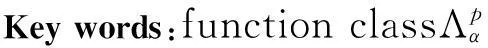
中图分类号：O174.5

文献标识码：A

文章编号：1001-9146(2015)06-0096-03

通讯作者：

作者简介：高丹丹(1991),女，河北衡水人，在读研究生，基础数学.肖建斌教授，E-mail:xjb@hdu.edu.cn.

收稿日期：2015-05-19

DOI：10.13954/j.cnki.hdu.2015.06.021