基于径向剖分的井地三维有限元电阻率与极化率模拟

黄俊革, 李林杰, 农观海,2, 闫怀超, 高文利, 林振洲

(1.上海应用技术学院 城市建设与安全工程学院，上海 201418;

2.桂林理工大学 地球科学学院，桂林 541004;

3.中国地质科学院 地球物理地球化学勘查研究所，河北 廊坊 065000)



基于径向剖分的井地三维有限元电阻率与极化率模拟

黄俊革1, 李林杰1, 农观海1,2, 闫怀超1, 高文利3, 林振洲3

(1.上海应用技术学院 城市建设与安全工程学院，上海 201418;

2.桂林理工大学 地球科学学院，桂林 541004;

3.中国地质科学院 地球物理地球化学勘查研究所，河北 廊坊 065000)

[摘要]采用径向剖分的有限元法对井地三维电阻率法进行数值模拟，以适应不同观测装置对数值模拟的要求。以井口为中心，将区域在环钻孔方向以45°夹角均匀剖分为八等分，再在直径方向上等距离剖分。径向剖分形成的单元呈环形分布，更符合井中电场的分布规律。与这种剖分相对应，设计了以井口为中心布置4条放射状测线(“米”字形)的井地观测装置，解决了井旁地质体位置未知的情况下难以确定观测方向的问题。通过对典型的地质模型进行有限元正演模拟计算，结果表明径向剖分数值模拟方法是可行的、准确的；以这种井地观测方式探测位置未知的地质体是行之有效的。

[关键词]井地；径向剖面；有限元；电阻率； 极化率

传统的井中电阻率测深大都采用单方向或向量激发的方式通过平行测线进行观测，在探测井旁盲矿、油气藏边界探查等领域得到广泛的应用[1]。基于勘查需求和应用领域的拓展，推动了井中电阻率测深的理论研究，如Wang等、Avdeev 等分别用有限差分和积分方程法对电阻率测井进行了三维模拟[2,3]；王志刚等对井地直流电法三维数值模拟及异常规律研究[4]。刘雪军等应用正演模拟方法研究供电电极在井中针对储集目标供电激发时，地下与地面电磁场的异常特征[1]；戴前伟等利用双频激电井地电位技术研究剩余油分布[5]；毛立峰等对井-地交流电法的矢量有限元三维正演问题进行了研究[6]；何展翔等在圈定油气藏、研究储层分布、油井的注水和注浆的动态监测方面均取得了一定的效果[7]；李长伟等研究了不同测量方式( 井-地，地-井，井-井) 下点源场井中电法的三维有限元数值模拟[8,9]；吕玉增等研究了地井五方位测量方法及正反演[10,11]；岳建华等研究了井-地三维电阻率成像技术及实现方法[12]。这些方法中，大都以地质体所在方位为主要探测方向，以井口为中心布置平行测网。在这样的探测方式中，地质体位置与探测异常的幅值有很大的关系，在探测之前必须确定正确的观测方向，才可以有效突出地质体异常，减少干扰异常；但在地下地质体位置未知的情况下，很难预先确定测线的布置方向。为此我们设计了以井口为中心布置4条放射状测线的井地径向观测装置，井中供电，地面测量相邻2个电极间的电位差，这样可以有效解决井旁盲矿体位置未知的情况下难以确定观测方向的问题，提高对井旁地质体的勘探能力，在探测地下水流向的工作中这种电极布设方式被广泛采用。针对这种观测方式，井地电法的数值模拟进行区域离散时，难以将其离散成六面体单元，且网格疏密不易控制，在剖分单元的3个方向上长度不能同时放大，造成网格剖分困难[8]。本文针对井中电场分布的特点和井地径向观测装置，设计了井地电场基于径向剖分的三维电阻率法有限元数值模拟方法，对目标区域进行统一的四面体剖分，以适应径向剖分多种网格单元并存的情况。通过对典型模型模拟计算并分析其异常特征, 结果表明该方法效果良好。

1井地径向电阻率、极化率观测方式

一般来说，为探测地下地质体，获得最大观测异常，应首先确定地下目标体的走向等信息，再确定观测主剖面、布置测网。井地径向三维电阻率、极化率测量方法使用的是单极—偶极装置,其基本思想是在井下以滚动形式进行点电源供电，地面上以井口为中心布置4条放射状(“米”字形)测线(图1)，测量测线上相邻电极之间的电位差，得到地下目标体视电阻率、视极化率信息。这种测量方式，无须预先确定观测主方位，便可得到地下地质体分布信息。

图1　井地径向剖面三维电阻率观测方式示意图Fig.1　Sketch of borehole-ground radial section 3-D resistivity survey method

2区域离散与单元分析

以有限单元法对区域进行三维模拟计算时，大都将观测区域均匀剖分成六面体，远离井口的大规模地质体需在3个方向(X、Y、Z)的剖分中占用很多剖分单元，剖分的适应性不佳。为了提高井地电法模拟的单元适应能力，我们采用以井口为中心，在直径方向(R方向)上、深度方向上(Z方向)等距离剖分，在环钻孔方向以45°夹角均匀剖分为八等分(图2)。采用这样的网格单元剖分方法对区域进行剖分，一方面使单元体积与单元到井孔的距离呈正比，即单元距离井口越远，单元体积越大，同样的剖分区域占用的网格数量大幅减少；另一方面，由于区域剖分单元以井口为中心环形分布，单元的一个边与电场等位线基本重合，与地井电场分布的实际情况更加吻合，提高了该单元节点之间的电位插值精度，从而可以提高正演的精度和速度。

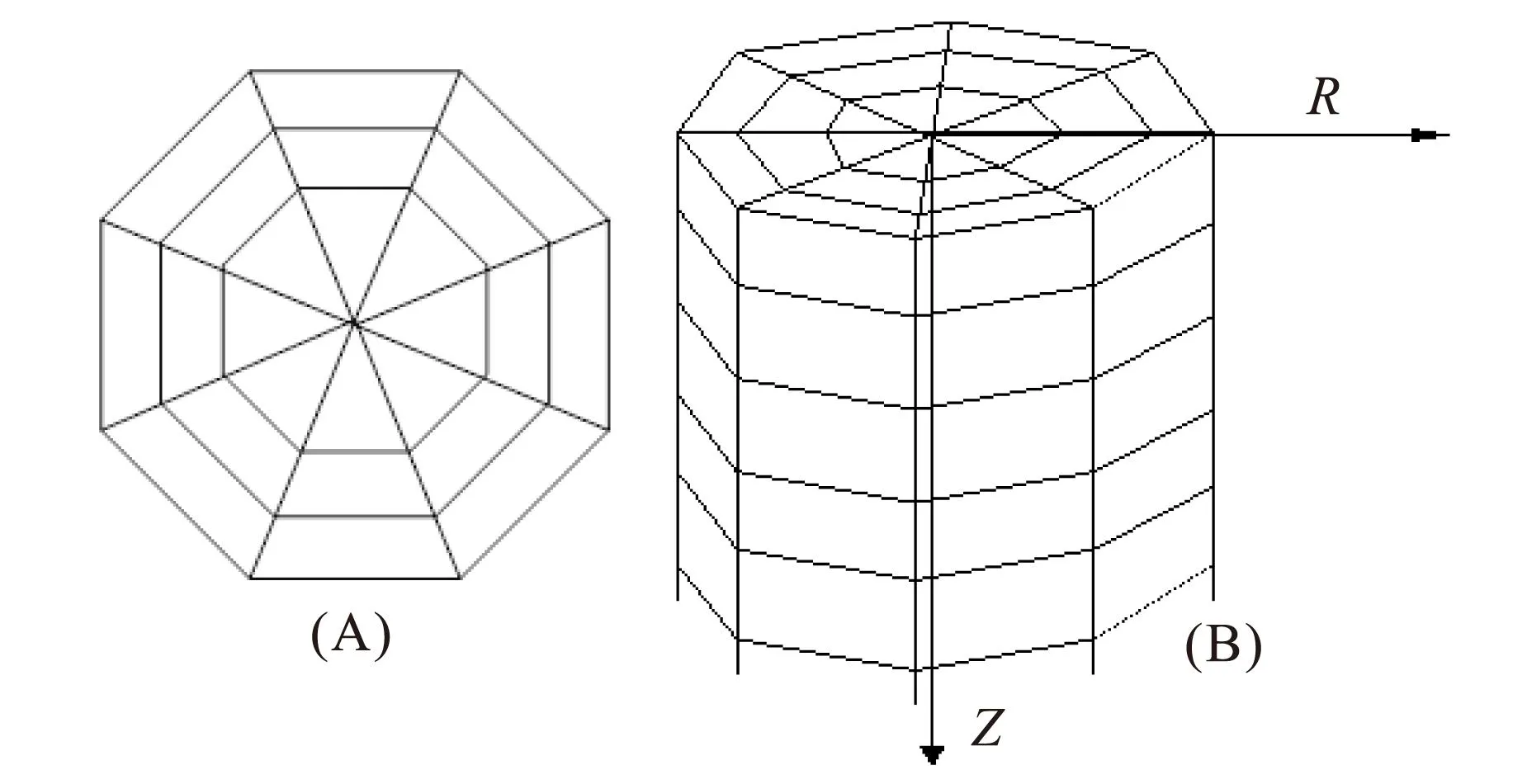
图2　三维空间剖分示意图Fig.2　Sketch of 3-D spatial division(A)目标区网格剖分俯视图;(B)目标区网格剖分侧视图

将区域进行剖分时，与井口相邻的单元被剖分成三棱柱，其他单元被剖分成水平截面为梯形的六面体(图3)。为了将网格剖分和算法统一，我们将每个六面体单元首先剖分成2个三棱柱单元, 再对每个三棱柱单元按照右手螺旋规则剖分成4个四面体，单元剖分规则和节点编号如图3所示。这样就可以实现在不增加节点数又能得到尽量多的剖分单元,从而达到提高有限单元计算精度的目的。

下面我们以节点编号为1, 2, 3, 5的四面体单元说明单元节点电位求解的过程。假设1, 2, 3, 5节点坐标分别为(x1,y1,z1), (x2,y2,z2), (x3,y3,z3), (x4,y4,z4);p(x,y,z)为四面体内部的一个点(图4)，p点的位置可写为以下4个表达式[13]

Li是x,y,z的线性函数，例如

其中

图3　模型单元剖分示意图Fig.3　Sketch of the model elements division(A)三棱柱体单元剖分示意图; (B)六面体单元剖分示意图

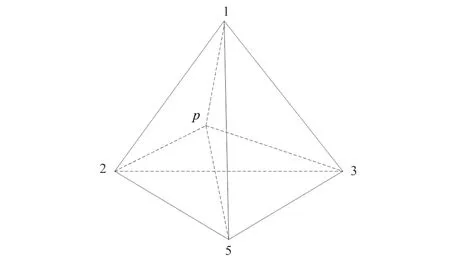
图4　四面体单元示意图Fig.4　Sketch of tetrahedron elements

是与四面体顶点坐标有关的常数。类似地，可得到L2,L3,L4。

单元中电位采用线性插值，u=α1x+α2y+α3z+α4,根据4个顶点的坐标和函数值，可确定4个系数α1, …,α4,可写成

其中形函数Ni=Li(i=1,…,4)。

为提高计算精度,采用三维电场的异常电位法求解[13],单元的电位列向量ue扩展成全体节点的电位列向量u，可以得到以下方程组

Ku=-K′u0

(1)

其中K和K′为系数矩阵，u为待求异常电位向量，u0为正常电位向量。井-地观测方式均匀半空间中的正常电位表达式为

(2)

式中的r′为镜像电源到观测点之间的距离。由于观测点位于地表，显然有r=r′，解线性方程组(1)，可得各结点的异常电位u，与预先计算的各节点正常电位u0相加，便可得到节点的总电位[14]。

3视极化率的计算

(3)

故

ηs=1-ρs2/ρs1

(4)

其中:ΔU为极化场电位差; ΔU1为一次场电位差; ΔU2为二次场电位差; ηs表示视极化率。

4数值算例与结果分析

4.1井旁低阻高极化模型

图5为一个直立井模型，井深20m。模型中井旁有一个棱柱地质体(位于南北方向测线第5断面下部，地质体的尺寸以及形状见图6)。其电阻率为5Ω·m，极化率为20%；围岩电阻率为100Ω·m，极化率为5%；地质体中心与井孔间的距离4m，距离地面6m。地面上以井口为中心布置4条放射状测线(图1)，供电点依次由浅及深(-1～-13m)供电，测量地面相邻两个电极的电位差，测线上2个测量电极之间的距离为1m。视电阻率、视极化率断面图成图规则是，以供电点深度为Z坐标，观测点中心坐标为X、Y坐标，共形成南北(5-1)、南西-北东(6-2)、西东(7-3)、西北-东南(8-4)方向4个断面。

图5　井旁低阻高极化模型示意图Fig.5　Schematic diagram of model 1

图6　异常体三维模型Fig.6　3-D model anomalous body

从图7(A)、(B)的低阻棱柱视电阻率南-北、东北-西南方向剖面可见，钻井两侧附近出现一对高幅值、直立脉冲形异常，钻井靠异常体一侧的脉冲异常为低阻，与地质体电性对应,另一侧为高阻。低阻脉冲异常顶部深度约为6m，呈下窄上宽的形态，低阻异常上部的宽度与地质体宽度基本一致。从图7(C)、(D)的视电阻率西-东、北西-南东方向剖面的异常特征图可见，除在井孔的两侧附近出现一对直立脉冲形异常外，脉冲异常的顶部出现一个扁平马鞍形低阻异常，与低阻地质体在断面上的投影位置和电性基本对应。总体来说，各方向断面均可见低阻体异常，且异常位置与地质体位置或地质体在断面上的投影位置相对应。

图7　低阻高极化地质体井地径向剖分数值模拟视电阻率断面Fig.7　Apparent resistivity sections on low resistivity & high polarizability geological body borehole-ground radially split numerical simulation

从视极化率剖面图(图8)可以看到，井孔两侧同样出现脉冲形高、低视极化率异常，高极化异常位于地质体一侧或与地质体投影位置相对应，最大异常达到9.8%，呈上宽下窄之势，异常外边缘与地质体外边缘对应良好。在各个方向的断面中均见极化率异常，位置对应良好，异常值大小与观测断面和地质体间距离相关。

为了检验计算结果是否准确，计算精度是否满足要求，利用较为成熟的井地三极测深装置六面体剖分数值模拟解与井地径向剖分的数值模拟结果进行对比。如图9(A)所示，低阻立方体棱长4m，电阻率5Ω·m，位于南北方向测线的下方，中心距离井孔4m，背景电阻率100Ω·m，供电点位于井中-1～-13m，观测点极距1m。对比图9(B)所示的视电阻率断面和图7(A)，异常形态基本相似。从表1的异常幅值的差异来看，均小于5%，两种模拟结果有差异主要是由于地质体体积差异所致。

4.2井旁高阻高极化模型

井旁高阻高极化模型的异常体位置、形态与井旁低阻高极化模型完全相同，只在电性上不同。异常地质体的电阻率为1 000Ω·m，极化率20%；围岩电阻率100Ω·m，极化率5%。

从模型的视电阻率断面(图10)来看，井孔深部两侧有2个纵向、性质相反的条带状异常，高阻异常位于南侧，与钻孔南侧地质体的性质相对应，异常顶部深度与地质体顶部基本吻合，但异常的位置与地质体对应不佳。

从视极化率断面来看，井孔的深部两侧出现了2组高低极化条带状异常，高极化异常位于高极化地质体一侧。除东西方向的视极化率断面(图11-C)与地质体的位置对应不佳外，其余断面的高极化与地质体的位置对应良好。这种情况，与东西方向的观测断面与地质体距离较大有关，而这一特征，更有利于地下地质体的定位。

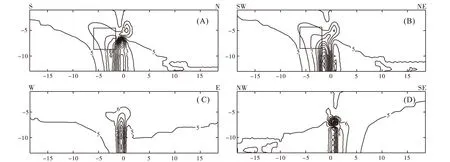
图8　低阻高极化地质体井地径向剖分数值模拟视极化率断面Fig.8　Apparent polarizability sections on low resistivity high polarizability geological & body borehole-ground radially split numerical simulation

图9　六面体模型及视电阻率断面图Fig.9　Schematic diagram of cube geological model and apparent resistivity section

观测点位视电阻率/Ω·mXYZ径向剖分六面体剖分相对误差/%观测点位视电阻率/Ω·mXYZ径向剖分六面体剖分相对误差/%0-18.5-3102.4103.5-1.10-8.5-389.486.63.20-17.5-3102.1103.3-1.20-7.5-387.084.03.50-16.5-3101.6102.9-1.30-6.5-385.483.81.90-15.5-3101.0102.4-1.40-5.5-385.586.4-1.00-14.5-3100.2101.7-1.50-4.5-387.791.0-3.70-13.5-399.2100.6-1.40-3.5-391.395.7-4.50-12.5-397.999.0-1.10-2.5-395.399.6-4.60-11.5-396.396.8-0.50-1.5-399.1102.4-1.30-10.5-394.393.90.50-0.5-3103.7106.0-2.20-9.5-392.090.31.800.5-399.495.14.4

4.3井孔穿过低阻高极化体模型

如图10(A)所示，模型中井孔穿过八棱柱低阻体(低阻地质体的尺寸以及形状参见图10-B)。八棱柱上表面距离地面4 m，纵向延伸4 m，低阻

图10　高阻高极化地质体井地径向剖分数值模拟视电阻率断面Fig.10　Apparent resistivity sections of high resistivity and polarizability geological body borehole-ground radially split numerical simulation

八棱柱电阻率5 Ω·m，极化率为20%；围岩电阻率为100 Ω·m，极化率为5%。这种模型主要针对地下水流速测定时，井孔中注以盐水等低电阻率模型而设计，主要勘察低阻高极化率物质被注入时视电阻率、视极化率的异常。

由于模型呈轴对称，各个方向的视电阻率、视极化率断面完全相同，因此仅呈现南北方向断面即可(图11-A、B)。图11(A)的视电阻率断面图显示，低阻马鞍状异常在宽度、深度方向的延展范围与低阻体形状基本一致，异常形态在水平方向上以井孔为中心对称分布。图11(B)所示的视极化率异常，在井孔周围出现一个圆锥形高低极化异常，上部中心为低极化异常，最大幅值-22%，

与异常体中心位置对应；两翼为10%左右的中极化异常，宽度与地质体吻合，呈对称分布；下部为以井孔为中心的高极化异常，最高异常幅值达到30%。 通过视电阻率和视极化率异常的位置与性质，可以推断地质体空间分布和电性。

4.4井孔穿过非对称形式的低阻高极化体模型

图12所示模型，为测定地下水流速时，井中注入低阻高极化率介质一段时间后，形成的低阻高极化率模型。上表面距离地面为4 m，纵向延伸6 m，低阻八棱柱电阻率10 Ω·m，极化率为10%；围岩电阻率为100 Ω·m，极化率为5%。

从图13和图11的视电阻率断面图对比来看，图13(A)的视电阻率异常在井孔南北两侧呈明显的非对称现象，井孔的南侧(-5～0 m)、视深度-4～-9 m之间存在明显的低阻异常，深部在井孔的南北两侧出现条带状异常。图13(B)的视极化率异常同样出现不对称现象，井孔的南侧(-5～0 m)、视深度-4～-9 m之间存在明显的高极化率异常，深部在井孔的南北两侧出现条带状异常。从视电阻率和视极化率的断面图中可以很好地判断水流的方向。

图11　高阻高极化地质体井地径向剖分数值模拟视极化率断面Fig.11　Apparent polarizability sections of high resistivity & high polarizability geological body borehole-ground radially split numerical simulation

图12　模型示意图Fig.12　Schematic diagram of models

图13　南-北方向视电阻率、视极化率断面Fig.13　Apparent resistivity and polarizability sections in south-north direction(A)视电阻率断面图; (B)视极化率断面图

图14　模型示意图Fig.14　Schematic diagram of a model

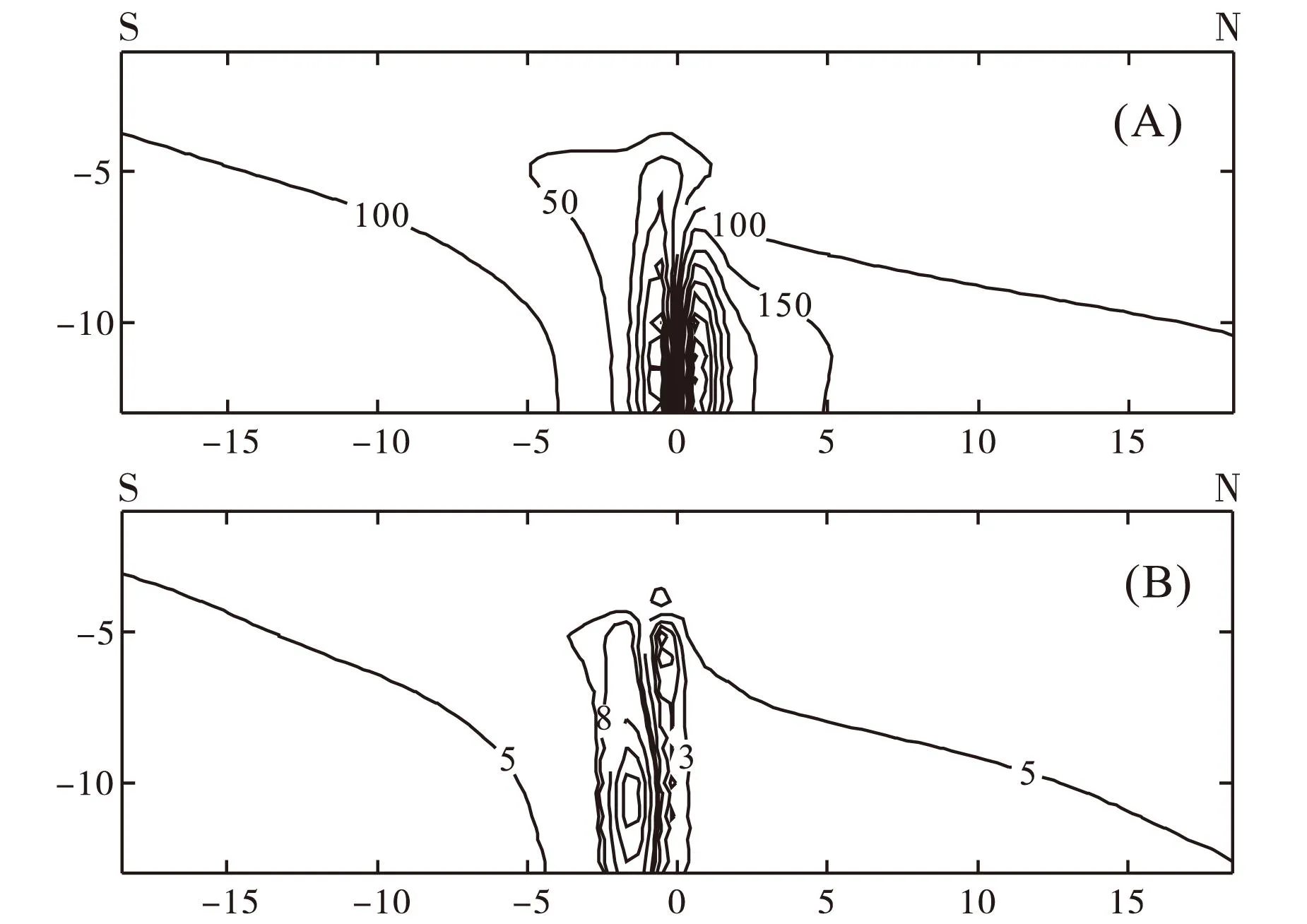
图15　南-北方向视电阻率、视极化率断面Fig.15　Apparent resistivity and polarizability sections in south-north direction(A)视电阻率断面图; (B)视极化率断面图

5结 论

本文给出一种适合井地电阻率、极化率观测的三维径向剖分的有限单元法数值模拟技术，通过与井地三极测深装置六面体剖分数值模拟结果进行比较，证明井地径向剖分数值模拟方法计算结果正确，满足异常分析的要求。通过对几个典型的地质模型的正演模拟计算, 分析其视电阻率和视极化率异常的分布规律，结果表明井地径向观测系统在探测位置未知的地质体是可行、有效的，尤其在地下水流向观测方面，径向剖分的数值模拟方式与观测装置的吻合性更好。

[参考文献]

[1] 刘雪军,王家映,何展翔,等.研究油气储集目标的井中地面电磁新技术[J].勘探地球物理进展,2006,29(2):98-101.

Liu X J, Wang J Y, He Z X,etal. Study of hydrocarbon accumulation by borehole-ground EM method[J]. Progress in Exploration Geophysics, 2006, 29(2): 98-101. (In Chinese)

[2] Wang T, Signorelli. Finite difference modeling of electromagnetic tool response for logging while drilling[J]. Geophysics, 2004, 69(1): 152-160.

[3] Avdeev D B, Kuvshinov A V, Pankratov O V,etal. Three dimensional induction logging problems, part 1: Anintegral equation solution and model comparisons[J]. Geophysics, 2002, 67(2): 413-426.

[4] 王志刚,何展翔,刘昱.井地直流电法三维数值模拟及异常规律研究[J].工程地球物理学报,2006,3(2):87-92.

Wang Z G, He Z X, Li Y. Research of three-dimensional modeling and anomalous rule on borehole-ground dc method[J]. Chinese Journal of Engineering Geophysics, 2006, 3(2): 87-92. (In Chinese)

[5] 戴前伟,陈德鹏,刘海飞,等.双频激电井地电位技术研究剩余油分布[J].地球物理学进展,2009,24(3):959-964.

Dai Q W, Chen D P, Liu H F,etal. Research of the residual oil distribution with dual frequency induced polarization and the borehole-to-surface potential method[J]. Progress in Exploration Geophysics, 2006, 29(2): 98-101. (In Chinese)

[6] 毛立峰,王绪本,何展翔.矢量有限元法在井-地交流电法三维正演问题中的应用[C]//中国地球物理学会第22届年会论文集.成都：四川科学技术出版社,2006:703-704.

Mao L F, Wang X B, He Z X. Application of vector finite-element method in 3D modeling on borehole-ground AC method[C]//22th Annual Conference of Chinese Geophysical Society. Chengdu: Sichuan Science and Technology Press, 2006: 703-704. (In Chinese)

[7] 何展翔,刘雪军,裘尉庭,等.大功率井-地电法油藏边界预测技术及效果[J].石油勘探与开发,2004,1(5):74-76.

He Z X, Liu X J, Qiu W T,etal. High-power surface-borehole electrical method in predicting reservoir boundary and its application[J]. Petroleum Exploration and Development, 2004, 31(5): 74-76. (In Chinese)

[8] 李长伟,熊彬,吕玉增.电法测井的三维有限元模拟[J].物探与化探，2012,36(4)：585-590.

Li C W, Xiong B, Lyu Y Z. Three-dimensional finite element modeling of electrical well logging[J]. Geophysical and Geochemical Exploration, 2012, 36(4): 585-590. (In Chinese)

[9] 李长伟,阮百尧,吕玉增,等.点源场井-地电位测量三维有限元模拟[J].地球物理学报,2010,53(3):729-736．

Li C W, Ruan B Y, Lyu Y Z,etal. Three-dimensional FEM modeling of point source borehole-ground electrical potential measurements[J]. Chinese Journal of Geophysics, 2010, 53(3): 729-736．(In Chinese)

[10] 吕玉增，阮百尧.地-井五方位IP异常特征与解释[C]//第九届中国国际地球电磁学术讨论会论文集.桂林：桂林工学院,2009:177-180.

Lyu Y Z, Ruan B Y. Anomalous characteristics and interpretation of surface-borehole 5-direction IP[C]//9th China International Geo-electromagnetic Workshop. Guilin: Guilin University of Technology, 2009: 177-180. (In Chinese)

[11] 吕玉增,阮百尧,彭苏萍.地-井方位激电观测异常特征研究[J].地球物理学进展,2012,27(1)：201-216.

Lyu Y Z, Ruan B Y, Peng S P. A study on anomaly of surface-borehole direction induced polarization survey[J]. Progress in Geophysics, 2012, 27(1): 201-216. (In Chinese)

[12] 岳建华,刘志新.井-地三维电阻率成像技术[J].地球物理学进展，2005,20(2):407-411.

Yue J H, Liu Z X. Three dimension resistivity tomography of mine-ground[J]. Progress In Geophysics, 2005, 20(2): 407-411. (In Chinese)

[13] 徐世浙.地球物理中的有限单元法[M].北京:科学出版社,1994.

Xu S Z. The Finite Element Methods in Geophysics[M]. Beijing: Science Press, 1994. (In Chinese)

[14] 黄俊革，阮百尧，王家林，等.钻井-地表电极联合电阻率观测装置的异常特征研究[J].地球物理学报, 2009,52(5):1348-1362.

Huang J G, Ruan B Y, Wand J L,etal. A study on anomaly of borehole-to-ground joint resistivity surveying system [J]. Chinese Journal of Geophysics, 2009, 52(5):1348-1362. (In Chinese)

3-D FEM modeling of borehole-ground resisitivity and

polarizability based on radial subdivision

HUANG Jun-Ge1, LI Lin-jie1, NONG Guan-hai1,2,

YAN Huai-chao1, GAO Wen-Li3, LIN Zhen-Zhou3

1.SchoolofConstructionandSafetyEngineering,ShanghaiInstituteofTechnology,Shanghai201418,China;

2.CollegeofEarthScience,GuilinUniversityofTechnology,Guilin541004,China;

3.InstituteofGeophysicalandGeochemicalExploration,CAGS,Langfang, 065000,China

Abstract:In order to fit different detecting installations, this paper makes 3-D modeling of the borehole-ground resisitivity and polarizability based on the radial division. Taking the well mouth as the centre, the region is equably divided into 8 sectors by 4 radial lines on the ground with the angle of 45° between two lines. Each sector is divided by a regular distance on radial line. The radial subdivision cells present a circular form, which is more coincidental with the distribution of an electric field. The paper designs the borehole-ground observation installation by setting 4 radial survey lines taking the well mouth as the center, thus, the surveying direction can be set under the unknown geologic bodies. The calculating of typical models shows that the subdivision method is correct and feasible. The surveying method by arraying around wells to detect the unknown position of geologic bodies is effective.

Key words:borehole-ground; radial subdivision; FEM; resisitivity; polarizability

[文献标志码][分类号] P631.3 A