裂缝性低渗油藏可动凝胶流动特性分析与渗流模型建立

安淑萍， 郑黎明， 赵　青

(1.陕西延长石油(集团)有限责任公司 研究院， 陕西 西安　710075； 2.中国石油大学(华东) 石油工程学院， 山东 青岛　266580)



裂缝性低渗油藏可动凝胶流动特性分析与渗流模型建立

安淑萍1， 郑黎明2， 赵青2

(1.陕西延长石油(集团)有限责任公司 研究院， 陕西 西安710075； 2.中国石油大学(华东) 石油工程学院， 山东 青岛266580)

摘要：可动凝胶深部调驱是微裂缝发育低渗特低渗储层水窜治理的重要手段，但现有可动凝胶渗流主要局限于均匀孔隙介质，微裂缝内流动和复杂储层渗流动力学模型研究均较欠缺.通过可动弱凝胶微裂缝渗流可视化实验，深入认识其在微裂缝这一孔隙结构中的流动特性.实验发现，可动凝胶微裂缝渗流表现出幂律流动形态、临界压力梯度、粘滞吸附、再次水驱潜在重新窜流风险等特点，渗流压力梯度受交联黏度、缝宽影响的敏感性较强.综合实验认识以及孔隙介质可动凝胶非线性渗流、低渗非线性渗流、双重介质渗流等数学模型，建立了微裂缝发育低渗特低渗储层可动凝胶调驱的数学模型，涵盖了流体运动、质量守恒、可动凝胶黏度特性等方程以及大裂缝优先调驱、非牛顿流体剪切、岩石孔渗吸附损伤、调驱过程微裂缝限压等系列附加判定指标，以尽可能贴近矿场调驱实际，为该类复杂储层可动凝胶渗流动力学分析提供基础.

关键词：微裂缝； 大裂缝； 低渗油藏； 可动凝胶； 渗流数学模型

0引言

裂缝性特低渗油藏中裂缝既是增加储层导流能力的主要孔隙结构，但又会在水驱开发中成为窜流的优势通道.尤其是当该类储层内部发育有大量天然微裂缝时，该类油藏的开发难度急剧增加.储层开发后期，产液逐渐下降，在面临增产提液要求下，油水井之间很快发生水窜，甚至出现暴性水淹.通过对储层多级高渗通道进行有效封堵，尤其是低黏度的可动凝胶等驱替进入储层内部[1,2]，增加水驱波及系数，成为了改善该类油藏开发后期效果的一个重要手段.

目前，围绕含裂缝多孔介质调驱(调驱剂以非牛顿流体作为主要研究对象)开展了大量的实验和理论研究，涉及了不同的调驱剂体系研制、调驱工艺优化和非牛顿流体(以可动凝胶为主)渗流规律分析[3-5].然而，在裂缝性低渗-特低渗油藏中，可动凝胶在微裂缝内的流动是制约整体封堵性能的主要因素，上述研究也仅主要针对非牛顿流体在均匀多孔介质中的渗流或交叉学科如压裂、钻井渗滤、岩体注浆中[6-8]非牛顿流体在裂缝-大裂缝内的宏观流动，而对调驱剂这一非牛顿流体在微裂缝以及裂缝性双重介质内部运移的研究较少.如马庆坤[5]分析了可动凝胶体系的渗流流变特性，建立了多参数的粘弹-触变性本构关系；舒刚[8]实验研究了中-大裂缝内聚合物CMC的流动；刘慈群[9]建立了弱压缩幂律非牛顿流体径向不定常渗流模型，并进行了简化数学分析；陈国[10]借鉴聚合物驱模型和组分模型，建立了均匀介质内的聚合物交联调剖驱油数学模型；崔英怀[11]综合可动凝胶体系流变特征、非线性渗流特征、一般质量传输方程，建立了均匀孔隙介质内可动凝胶体系驱油渗流数学模型.上述实验和理论研究给出了可动凝胶渗流特性，但存在研究裂缝较宽、裂缝内流体为聚合物、调驱剂在均匀孔隙介质中流动而未涉及裂缝这一结构等局限.

因此，以可动弱凝胶为驱替介质，开展非牛顿流体在微裂缝内的流动性实验，结合非牛顿流体流变特性、双重介质渗流力学理论，建立双重介质油藏非牛顿流体驱替模型，将指导微裂缝发育的双重介质油藏调驱渗流规律研究，对该类油藏设计施工方案、提高封堵效果提供理论支撑.

1可动弱凝胶微裂缝渗流特性实验

采用鄂尔多斯盆地某油田模拟地层水配置可动弱凝胶体系，将其在不同缝宽、驱替速率条件下注入微裂缝模型，分析可动弱凝胶在微裂缝中渗流特性.

1.1　实验材料与仪器

(1)实验材料：有机铬交联剂与聚合物HPAM的交联比为1∶60，聚合物质量浓度为0.25 g/L，可动凝胶交联曲线与模量测量如图1所示；模拟地层水.

(2)实验仪器：多功能采油驱替系统，Brookfield DV Ⅲ型旋转粘度计，磁力搅拌器，恒温箱，自制的可视化微裂缝模型(如图2所示)，压力表，真空泵.

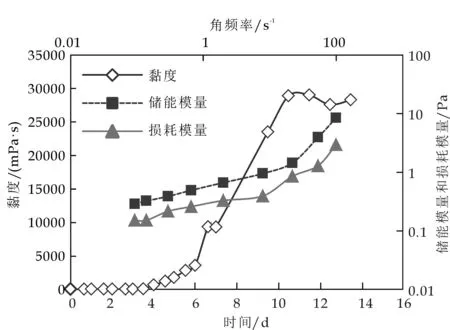
图1　可动凝胶交联曲线与模量

图2　可动弱凝胶微裂缝可视化驱替实验装置

1.2　实验步骤

连接实验装置，如图2所示，检查裂缝模型的密封性；开泵注入模拟地层水；切换阀门，将候凝36 h的可动凝胶注入微裂缝模型(缝宽30μm)，注入速度0.1 mL/min，记录不同时间下模型压力变化；停泵、清洗模型，重新将候凝96 h的可动凝胶注入中间容器，重复进行驱替，对比分析不同黏度的可动凝胶微裂缝流动规律；改换为缝宽为80μm的微裂缝模型，重复上述实验，对比分析不同缝宽条件下可动凝胶流动变化.

2结果与讨论

2.1　实验结果

裂缝性低渗特低渗油藏中，微裂缝这一孔隙结构具有较高的导流能力，可以明显降低储层的流动压力.根据微裂缝可动凝胶驱替实验(如图3和图4所示)得到，在相同注入速度和缝宽(30μm)条件下驱替可动凝胶，随注入时间的增加，可动凝胶在微裂缝中的流动阻力逐渐增加，不同初始交联强度下的可动凝胶在微裂缝中的流动阻力不同，注入时初始黏度越大，裂缝两端压力梯度亦越大.当初始黏度较低时，裂缝两端压力梯度缓慢增加，当初始黏度较高时，裂缝两端压力梯度先缓慢增加后呈抛物线型急剧上升.

图3　不同初始交联黏度下可动凝胶流动

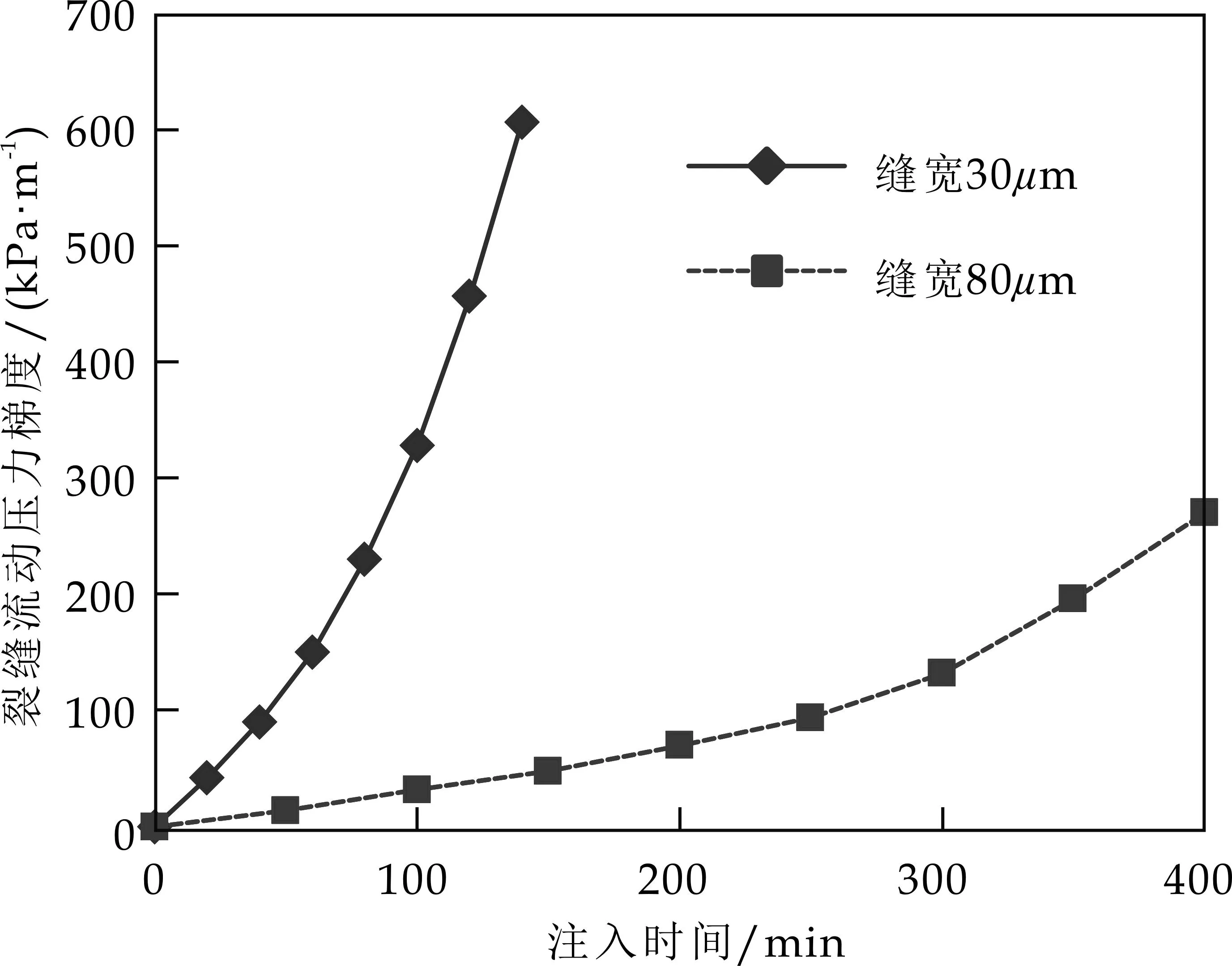
图4　不同缝宽条件下可动凝胶流动

在相同注入速度和初始交联强度(黏度100 mPa·s)条件下驱替可动凝胶，随缝宽的增加，可动凝胶在微裂缝中的流动阻力急剧降低，说明较窄微裂缝可动凝胶具有相对较差的流动性，储层调驱时堵剂优先进入宽裂缝.

2.2　分析与讨论

裂缝内幂律非牛顿流体流动公式为

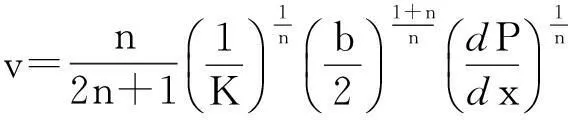
(1)

实验用可动凝胶在微裂缝中的渗流表现出明显的幂律流体流动特性，驱替过程中凝胶弹性模量的逐渐增强与黏性模量的逐渐降低，使得整体黏度发生改变，微裂缝中可动凝胶压力梯度呈指数性上升.微裂缝中的可动凝胶流动与聚合物表现出一定的相似性，均具有随注入速度增加，压力梯度快速增加的幂律流动形态.但可动凝胶微裂缝流动又不同于聚合物流动[8]，聚合物黏性模量要大于可动凝胶，当启动压力梯度较小、黏度较低时，聚合物在微裂缝的流动阻力要大于可动凝胶，但当压力梯度较大时，聚合物又表现出较强的黏弹-触变性，聚合物黏度急剧下降，而可动凝胶黏度降低幅度明显小于聚合物.

对于不同的裂缝缝宽，可动凝胶的流动阻力不同，随缝宽的减小，相同注入速度下压力梯度明显增大.但在微裂缝内的流动受到粘附层阻力影响与较强的剪切稀释作用，可动凝胶流动表现出与孔隙介质中渗流的相似性，较高压力梯度下流动趋于层流；当裂缝较宽时，可动凝胶受到的剪切稀释作用降低，流体流动趋于层流-紊流的过渡阶段[4].

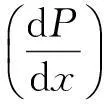
实验过程中，发现可动凝胶在微裂缝中驱替时，在粘附层的影响下亦表现出一定的吸附滞留特点，在双重介质可动凝胶驱替渗流力学模型建立时，应同样考虑裂缝表面的滞留.可动凝胶在微裂缝中的封堵还表现出一定的疏松性，当可动凝胶在模型中候凝以后再次进行水驱，如图5所示灰色连续相为水相，微裂缝中的可动凝胶(图中透明区域)间仍然具有一定的渗透性，相对其他未封堵高渗通道明显降低，但又明显高于低渗-特低渗的基质；这表明可动凝胶在具有一定液流转向作用的同时，同样保留再次形成新的次级窜流通道的可能性.实际矿场调驱时，应通过调驱工艺改进，增加微裂缝中的堵剂封堵强度与致密性，提高调驱的有效期，增加原油开发效果.

图5　可动凝胶候凝后再次水驱时流体分布形态(灰色连续相为水相)

3微裂缝发育低渗储层可动凝胶渗流数学模型建立

基于上述可动凝胶微裂缝渗流实验，流体表现出幂律流动形态、临界压力梯度、缝宽的敏感性和粘滞吸附等一系列特点，因此，在进行发育微裂缝双重介质中可动凝胶渗流数学模型建立与分析时，应补充相应的运动方程和辅助方程.

然而，目前已有常规孔隙介质的可动凝胶体系非线性渗流数学模型、单独宽裂缝的非牛顿流体流动模型，而关于发育多级裂缝的低渗多重介质可动凝胶驱替模型尚无报道.因此，在综合上述模型与双重介质渗流模型、天然微裂缝等效介质连续模型基础上，结合实验模拟流动规律，尝试建立可动凝胶在发育微裂缝的双重介质中的渗流数学模型，为该技术在裂缝性低渗油藏应用的理论解释与矿场优化提供指导.

假设条件：裂缝性低渗特低渗储层为均质、各向同性，大裂缝、微裂缝、基质均匀分布，整体满足Warren-Root模型[12]；两类介质中的油水流动符合达西流动，裂缝内调驱剂符合非达西流动；基质只有油水两相，调驱剂只通过裂缝；基质内流体流向微裂缝、存在窜流质量交换，微裂缝内流体再流向大裂缝、存在窜流质量交换；流体、基质、裂缝均可压缩；调驱剂只在微裂缝内受到剪切作用，在大裂缝内忽略剪切作用，大裂缝和微裂缝内各相流动满足同一相渗规律.

3.1　流动方程

裂缝发育储层流动包括了微裂缝、大裂缝和基质的流动，表示为三重介质驱替模型.假设基质、微裂缝和大裂缝分别具有孔隙度φm、φf1、φf2和渗透率km、kf1、kf2.采用经典的分流量数学模型[13]，其中油水两相流动方程为

(2)

(3)

调驱剂的流动方程为[4，11]

(4)

式(2)~(4)中:下标i=o，w，p分别表示油、水、调驱剂三相；j=1，2分别表示微裂缝和大裂缝；下标m、f分别表示基质和裂缝；v为渗流速度，m/s；Pi为i相的压力，MPa；λm为基质启动压力梯度，MPa/m；k为基质或裂缝的绝对渗透率，10-3μm2；kr为基质或裂缝中各相的相对渗透率，当基质和裂缝相对渗透率取同一曲线时，需对油水相进行归一化处理；μ为流体黏度，mPa·s；R为裂缝内的各相流体渗透率下降系数，无因次.

3.2　质量守恒方程

对于裂缝性低渗特低渗油藏，各孔隙类型间存在窜流条件下基质、微裂缝和大裂缝内的连续性方程为

(i=o,w)

(5)

(i=o,w,p)

(6)

(i=o,w,p)

(7)

式(5)~(6)中:ρi为流体密度，kg/m3；Smi为流体饱和度，小数；φ为孔隙度，在调驱过程中由于滞留吸附会发生变化，因此需要辅助方程进行迭代；u1m*、u2m*、u12*分别为微裂缝与基质、大裂缝与基质、微裂缝与大裂缝间的窜流，参考Barrenblatt拟稳态窜流公式，假设

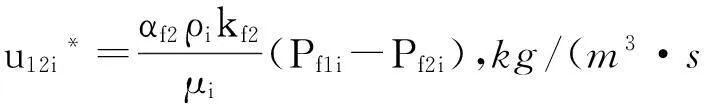
3.3　辅助方程

3.3.1绝对渗透率

对于低渗、特低渗储层，多孔介质渗透率随着孔隙压力的变化发生改变，将渗透率与孔隙压力表示为如下指数关系形式[14]:

km=km0exp[-β(Pm-P0)]

(8)

式(8)中:基质内孔隙压力采用体积平均方法获得，Pm=(1-Smw)Pm0+SmwPmw，MPa；β为渗透率变化系数，MPa-1；km0为孔隙压力P0为时的初始渗透率，10-3μm2.

3.3.2相渗方程

结合水驱时Van Genuchten油水相相渗函数和可动凝胶-水相相渗规律[4，11，15]，给出水、油两相和水、油、可动凝胶三相的相对渗透率如下，其中只有水、油两相时，

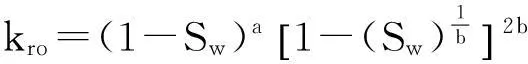
(9)

水、油、可动凝胶三相时，水相同上，可动凝胶体系水溶液、油相对渗透率为

(10)

式(9)~(10)中:a、b分别为水驱时油、水相的相渗方程系数，无因次；ak1、ak2为可动凝胶相对渗透率方程中的参数，无因次；X为交联体系交联剂与聚合物浓度之比，小数.

3.3.3毛管力方程

油、水相和油、凝胶相间的毛管力分别如下:

Pcw=Po-Pw,Pcp=Po-Pp

(11)

式(11)中:Pcw为油、水相间的毛管力，MPa；Pcp为油、凝胶相间的毛管力，MPa.

3.3.4密度变化

岩石和流体的状态方程如下[16]:

ρi=ρi0exp[Ci(Pji-P0)]

φm=φm0+Cm(Pm-P0)

φfj=φfj0+Cfj(Pfj-P0)

(12)

式(12)中:ρi0为流体初始密度，kg/m3；Ci、Cm、Cfj分别为流体、骨架基质和裂缝的体积压缩系数，MPa-1；P0为初始孔隙压力，MPa；φm0、φfj0分别为骨架基质和裂缝的初始孔隙度，小数；基质和裂缝内孔隙压力采用体积平均方法获得，即

Pfj=(1-Sfjw-Sfj0)Pfjp+SfjwPfjw+SfjoPfjo，MPa.

3.4　微裂缝张启压力

对于裂缝性低特低渗储层，当孔隙压力过高时会引起部分原油闭合微裂缝的张启，此处仅仅考虑微裂缝的张启，会引起基质、微裂缝、大裂缝间的孔隙分布比例改变.当微裂缝内的压力小于该临界张启压力时，原有孔隙结构分布比例保持不变，这也是调驱和后续注水过程需要达到的施工指标之一.天然裂缝的开启主要受水平主应力的影响，采用吴忠宝微裂缝张启压力公式如下[17]:

Pcf1=H[sinθ·(Fmax-Fmin)+Fmin]

(13)

式(13)中:Pcf1为微裂缝开启压力，MPa；H为油层某一点深度，m；Fmax、Fmin分别为最大与最小水平主应力梯度，MPa/m；θ为裂缝走向与最大水平主应力夹角，°；df1、df1′分别为微裂缝张启前、后的线密度，条/m.

3.5　可动凝胶黏度特性方程

3.5.1黏度变化

与单纯聚合物驱和孔隙介质可动凝胶驱不同，含裂缝低渗储层中可动凝胶在大裂缝中的触变性相对微裂缝内可进行忽略，只考虑微裂缝内的黏度触变，大裂缝内凝胶黏度此处只考虑随时间的变化.采用陈国交联调剖剂的黏度变化公式，可动凝胶黏度与聚合物浓度、体系各组分浓度、pH和成胶时间均有关[10].

(14)

式(14)中:Cp、Cg分别为聚合物和交联剂的浓度，Cg=XCp，mg/L；t为时间，min；tgei为成胶时间，min；Ca,max为酸组分的最大注入浓度，mg/L；A、B为交联函数的系数，无因次；μpoly(Cp,Cg)为参考酸浓度Ca,ref下当聚合物、交联剂浓度分别为Cp和Cg时凝胶的黏粘度，mPa·s.tgel、Ca,max、A、B、μpoly均由实验测定.

当超过一定黏度和驱替压力梯度时，室内发现可动凝胶在微裂缝内将不再流动，该临界条件主要受黏度的影响，因此定义裂缝内可动凝胶的临界黏度μpC，且满足

μp(t)≥μpC时，vfjp=0

(15)

3.5.2微裂缝内可动凝胶的剪切流变性

只考虑微裂缝内的可动凝胶黏度剪切作用，利用Carreau-Yasuda模型模拟孔隙介质内的剪切流变性[18]，即

(16)

式(16)中:γ为剪应变速度，即剪切率，s-1；μ0、μ∞分别为初始黏度和极限剪切黏度，mPa·s；λ为描述幂律流体剪切作用过渡区黏度变化的时间常数，s.

3.5.3渗透率降低系数

由于可动凝胶在裂缝内的吸附、捕集、滞留，造成裂缝绝对渗透率，该渗透率降低系数与体系浓度和体系性质有关.

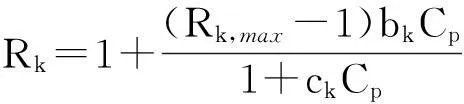
(17)

参考崔英怀、吴行才等[4，11]的可动凝胶渗流模型研究，渗透率降低系数亦可利用含油情况下的残余阻力系数进行表示.

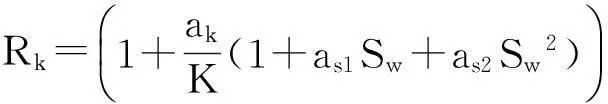
(18)

式(17)~(18)中:ak、bk、ck为方程系数，无因次；Rk.max为最大渗透率降低系数，无因次；as1、as2分别为吸附方程和动力学捕集滞留方程中的系数，无因次.

3.5.4孔隙度降低

在大量渗流数学模型研究中，往往只考虑渗透率的损害，而忽略了方程迭代中的孔隙度变化.可动凝胶在裂缝内同时会造成渗透率和孔隙度的降低，对于孔隙度的降低可通过渗透率的降低系数进行体现，也可通过裂缝的水力半径变化进行表示，即

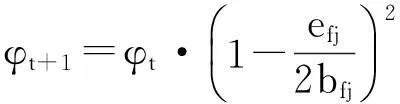
(19)

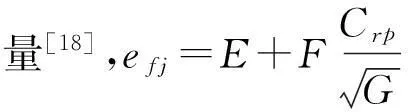
通过联立油、水、可动凝胶三相在多级裂缝和基质中的流动方程、质量守恒方程，代入流固相的辅助方程，建立得到微裂缝发育低渗储层可动凝胶渗流控制模型，通过数值离散化，并在迭代求解中进行微裂缝张启压力、可动凝胶黏度特性方程的数学判别，从而得到下一时刻多重介质各相流体压力-饱和度关系式.参考组分模型矩阵求解方法，综合压力-饱和度矩阵系数、初始边界条件，从而求解得到微裂缝发育低渗储层可动凝胶调驱后的流体饱和度再分布，揭示该类油藏多级裂缝窜流通道的液流转向调驱效果.

4结论

(1)裂缝性低渗特低渗油藏中，微裂缝这一孔隙结构可明显降低储层渗流阻力，在水驱开发后期，是导致油水井严重水窜的重要原因，进行可动凝胶在微裂缝的渗流研究，可深入认识该类储层深部调驱过程，为矿场调驱提供理论指导.实验发现，可动凝胶微裂缝渗流表现出幂律流动形态、临界压力梯度、缝宽的敏感性、粘滞吸附、再次水驱潜在重新窜流风险等特点；可动凝胶在微裂缝中的渗流压力梯度随注入初始黏度的增大、微裂缝缝宽的减小而急剧增加；宽裂缝是堵剂的优先注入通道.

(2)综合可动凝胶微裂缝渗流实验、均匀孔隙介质可动凝胶非线性渗流模型、双重介质渗流模型，尝试建立了微裂缝发育的低渗特低渗储层可动凝胶渗流数学模型，给出了基质、微裂缝、大裂缝中的可压缩水、油、可动凝胶三相流体的运动方程、质量守恒方程、辅助方程、微裂缝张启压力、可动凝胶黏度特性方程，考虑了低渗储层非线性渗透、可动凝胶裂缝优先流动、非牛顿流体微裂缝优先剪切、凝胶吸附对岩石孔渗的伤害、调驱过程微裂缝限制张启扩展等指标，尽可能贴近实际调驱矿场实际要求，为该类储层可动凝胶调驱动力学机制分析提供理论模型基础.

参考文献

[1] 马涛，何建华，王海波，等.可动凝胶颗粒在储层中的封堵性能研究[J].胶体与聚合物,2015,33(1):14-16，19.

[2] G.L.Lei,L.L.Li,H.A.Nasr El Din.New gel aggregates to improve sweep efficiency during waterflooding[J].SPE Reservoir Evaluation & Engineering,2011,14(1):120-128.

[3] A.H.Imqam,B.J.Bai,C.M.Xiong,et al.Characterisations of disproportionate permeability reduction of particle gels through fractures[C]//SPE Asia Pacific Oil & Gas Conference and Exhibition. Adelaide：Society of Petroleum Engineers,2014：1-14..

[4] 吴行才，朱维耀，马庆坤，等.可动凝胶体系非线性渗流特性及数学模型研究[J].石油钻采工艺，2006，28(5)：42-45.

[5] 马庆坤，朱维耀，高珉，等.可动凝胶体系渗流流变特性及其表征[J].石油学报,2007，28(5):85-88.

[6] 郭建春，刘恒，曾凡辉.裂一缝变缝宽形态对压裂井长期产能的影响[J].中国石油大学学报(自然科学版),2015,39(1):111-115.

[7] 杨米加,贺永年,陈明雄.裂隙岩体网络注浆渗流规律[J].水利学报，2001，46(7)：41-46.

[8] 舒刚.裂缝性地层钻井溢漏同存流动规律及模型研究[D].成都：西南石油大学，2012.

[9] 刘慈群.幕律非牛顿流体渗流[J].大庆石油地质与开发，1990，9(3):52-57.

[10] 陈国,赵刚,马远乐.聚合物交联调剖驱油数学模型[J].清华大学学报 (自然科学版),2004，44(12):1 606-1 609.

[11] 崔英怀，朱维耀，孙玉凯，等.可动凝胶体系非线性渗流数学模型[J].辽宁工程技术大学学报(自然科学版)，2009，28(S):283-285.

[12] 刘洋，李世海，刘晓宇.基于连续介质离散元的双重介质渗流应力耦合模型[J].岩石力学与工程学报,2011,30(5):951-959.

[13] 黄朝琴，高博，王月英，等.基于模拟有限差分法的离散裂缝模型两相流动模拟[J].中国石油大学学报(自然科学版)，2014，38(6):97-105.

[14] 舒卫兵, 许鹤华, 万菊英，等.低渗透油藏毛细管压力动态效应的数值模拟研究[J].水动力学研究与进展，2014，29(2):189-196.

[15] W.C.Lo,G.Sposito.Wave propagation through elastic porous media containing two immiscible fluids[J].Water Resources Research,2005,41(2):1-20.

[16] 刘振宇，翟云芳，卓兴家，等.非牛顿流体在多孔介质中的非稳态流动[J].大庆石油学院学报，1995，19(4):18-21.

[17] 吴忠宝，胡文瑞，宋新民，等.天然微裂缝发育的低渗透油藏数值模拟[J].石油学报，2009，30(5):727-730,734.

[18] 孙传宗.聚合物驱微观渗流机理研究[D].青岛：中国石油大学(华东)，2009.

【责任编辑：蒋亚儒】

Experimental seepage characteristics and mathematic seepage

model of flowing gel in low permeability reservoir

with natural micro-fractures

AN Shu-ping1, ZHENG Li-ming2, ZHAO Qing2

(1.Research Institute of Yan Chang Petroleum (Group) Co., Ltd., Xi′an 710075, China; 2.College of Petroleum Engineering, China University of Petroleum (East China), Qingdao 266580, China)

Abstract:Flowing gel deep plugging is a key method for water channeling treatment in low permeability reservoir developed with a mass of natural micro-fractures.However,available researches about flowing gel treatment are mainly focused on the non-linear seepage of flowing gel in homogeneous porous media or filed tests.An experiment about flowing gel displacement in visual micro-fracture is carried out,in which an insight into the flow characteristics of gel in a particular pore structure is viable.Characters as movable gel micro-seepage flow of power-law flow,critical pressure gradient,sticky adsorption,risks of channeling again in secondary water-flooding are found with the micro fractures.A higher pressure gradient in gel displacement is watched with the higher initial cross-linking viscosity and narrower fracture width.Then,modeling on the flowing gel displacement in the low permeability reservoir developed with natural micro-fractures and wide fractures is attempted.The above experimental recognition are combined with the non-linear seepage of the flowing gel in the homogeneous porous media,the non-linear flow in low permeability reservoir,and the double porosity media flow.Therein considers three phases-water,oil and flowing gel. Motion equation,mass conservation equation and viscous character equation of flowing gel in the matrix,micro-fractures and wide fractures are established.To approaching the actual filed plugging,a series of judgment requirements,as prior plugging in the wide fractures,non-Newton fluid shear thinning in micro-fractures,permeability and porosity damage in the fractures by adsorption and limited displacement pressure against micro-fracture open or propagation,are also append.It may provide a basis for the dynamic explanation for the actual deep plugging and fluid redistribution.

Key words:micro fractures; wide cracks; low permeability reservoirs; flowing gel; mathematic seepage model

中图分类号：TE319

文献标志码：A

文章编号：1000-5811(2016)01-0107-07

作者简介:安淑萍(1969-)，女，陕西延长人，工程师，研究方向：低渗油藏油气田开发

基金项目：国家重大科技专项项目(20011ZX05009-004)； 国家自然科学 (51274229)

收稿日期:*2015-10-26 *2015-11-17