蒙特卡罗方法对偏振光在大气中传输特性的研究

胡来归，向洲鹏，隋成华，鄢　波，陈乃波

(浙江工业大学 理学院,浙江 杭州 310023)



蒙特卡罗方法对偏振光在大气中传输特性的研究

胡来归，向洲鹏，隋成华，鄢波，陈乃波

(浙江工业大学 理学院,浙江 杭州 310023)

摘要：光在大气中传输的偏振特性由于其潜在的应用价值，近年来引起了人们极大的研究兴趣.为此，采用斯托克斯矢量描述光子偏振态，通过Mie理论递推公式计算散射相位函数与拒绝算法选取散射角，利用蒙特卡罗方法模拟光子在大气中的散射情况.针对最普遍存在的前向散射现象，首先在波长为350～750 nm时水平线偏振光、45°线偏振光及右旋圆偏振光等三种情况下入射到大气时其出射面的偏振度的变化情况；其次对偏振光穿过粒径为1 000～1 500 nm的气溶胶时其出射面偏振度变化情况进行了分析.模拟实验结果为偏振光在大气中的传输问题研究提供了一定的帮助.

关键词：蒙特卡罗；mie散射；气溶胶；偏振光

由于光在大气中传输的偏振特性有着巨大的应用价值，近年来，针对大气对光的散射和衰减作用进行的研究日益增多.光在大气中的传输是一个异常复杂的问题，究其原因在于其组成的复杂性，譬如大气中包含众多的气体分子、气溶胶粒子和降水质点[1-2].大多情况下，当光在诸如大气这样的不均匀介质中传输时，介质会完全破坏掉光的偏振特性，同时散射光的退偏特性也将变得随机.研究光在大气中的传输问题，偏振变化是一个很重要的因素及切入点，偏振光与不同粒径、浓度的散射粒子作用后，散射光所表现出来的偏振特性也会不同，有别于其他诸如测量光强、光谱、相位等常规方法.此外，散射光的偏振特性也会因入射光波长的变化而变化.因此，研究偏振光在大气中传输对大气污染物、有害气体的检测及空间目标的探测的领域存在重要的应用价值[3-10].然而目前，针对偏振特性的研究，因系统本身的复杂性，尚未能形成一个准确、完备的体系.笔者主要利用Mie散射理论建立蒙特卡罗计算平台，用斯托克斯矢量表征偏振特性[11]，对不同偏振光在不同散射介质中的传输特性进行了定性和定量的分析.

1理论基础

1.1Mie氏散射理论

1908年，德国科学家Gustav Mie从麦克斯韦方程组出发，对水平线偏振单色波被一位于均匀介质中任意直径和成分的均匀球颗粒衍射，得到了一个严格的数学解，即所谓的Mie氏理论[12].

如图1所示，当光强为I0、波长为λ的偏振光沿z轴照射到各向同性的球形颗粒时，其中θ为散射角，φ为入射光振动平面与散射平面间的夹角，那么，垂直散射面的散射光强I、平行于散射面的散射光强Il以及总散射光强Is三者可分别表示为

图1　气溶胶粒子对光的散射示意图Fig.1　Schematic diagram of light scattering aerosol particles

(1)

(2)

(3)

(4)

(5)

式中：an，bn为Mie散射系数，表达式为

(6)

(7)

式中：m为颗粒折射率；a为颗粒尺寸参数，即a=πD/λ，其中

(8)

(9)

表示ψn和ζn分别对各自变量的微商.πn，τn为散射角函数，其表达式为

(10)

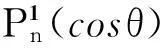
求出散射系数an，bn以及散射角函数πn，τn.便可求出散射光强i1(θ)和i2(θ).

1.2Mie散射光强的计算

1.2.1散射角函数πn，τn的计算

令ζ=cosθ，利用勒让德递推公式[13]可推导出

(11)

(12)

1.2.2散射系数an，bn的计算

由式(6，7)可以看出：只要推导出ψn(z)，ζn(z)递推公式，就可以求出an，bn的值.将散射系数改写成

(13)

(14)

式中ζn(z)可用ψn(z)表示为

ζn(z)=ψn(z)+iχn(z)

(15)

(16)

而Lentz证明有如下关系：

(17)

(18)

当k→∞时，[ak+1ak·…·a1]≈[ak+1ak·…·a2]，故可由式(18)递归出满足精度要求的Dn(z).而ψn(z)和χn(z)满足如下递推关系：

(19)

(20)

(21)

(22)

将初值ψ0(z)=sinz，ψ-1(z)=cosz，χ0(z)=cosz，χ-1(z)=-sinz分别代入式(19～22)，即可求出ψn(z)，χn(z)的各级函数值，再根据式(15)，可求出ζn(z).至此，式(13，14)中的未知数已全部求出，便可以求出散射系数[13-15].

1.3蒙特卡罗方法

蒙特卡罗方法的主要理念是，对于某些可以直接或间接的用一个随机过程来描述处理的问题，若所求的恰好是某事件出现的概率、或是某随机变量的期望时，可通过运用某种另外的方法，得出该事件出现的概率或平均值，并以它们作为原问题的解.

利用蒙特卡罗方法可以直接模拟大气辐射传输模型的传输过程，将其中光散射的过程等效为光子与大气介质中的粒子的碰撞过程，而碰撞自由程与消光系数有关，碰撞之后光子将改变前进方向，其散射角又由相函数确定，于是对大量光子进行跟踪统计就可得到所求问题的结果.蒙特卡罗模型主要包含以下几个部分：1) 发射光子(坐标系、方向余弦的选取等)；2) 光子运动；3) 光子吸收；4) 光子的散射；5) 光子的反射和折射；6) 运动终止.具体过程参考文献[16].

2模拟结果

根据文献[17]，大气气溶胶复折射指数的实部在1.4～1.67之间分布，虚部值大部分分布在0.00～0.02之间.笔者模拟中ka取值为0，n取值为1.59，综合计算速度与计算精度，光子数取107个.

2.1波长对出射偏振度的影响

模拟试验中，最大碰撞次数取10 000次.在380～730nm波长范围内，对水平线偏、45°线偏以及右旋圆偏等三种不同的偏振入射光进行模拟，模拟结果如图2所示.

图2　不同波长偏振光入射出射面偏振度Fig.2　Polarization of exit surface, when the incident light is polarized light with different wavelengths

据图2可知：偏振度表现出一定的波动性，波长对偏振度的影响总体不大，随着波长的增大，偏度均值在减小.

2.2粒径对出射偏振度的影响

入射波长取460 nm，碰撞次数取10 000次，对大气气溶胶粒径为1 000～1 500 nm，在水平线偏、45°线偏偏及左旋圆偏等三种偏振光入射情况下进行模拟，模拟结果如表1所示.

表1　偏振光入射到不同直径气溶胶其出射面偏振度

从表1可以看出：粒径并对出射光偏振度的影响并不明显，也没表现出统一的规律，相比而言，大气气溶胶粒径对圆偏振光的影响稍微大些，对线偏、45°线偏的影响表现不明显.

2.3碰撞次数对偏振度的影响

实验中入射波长采用460 nm，碰撞次数分别取10 000～60 000次，为减小光子数、碰撞数带来的误差，进行5次实验取平均值，5次模拟取完平均值，其结果如表2所示.

从表2可以看出：随着碰撞次数的变化，入射光为线偏和圆偏其出射偏振度基本无变化，入射光为45°线偏其出射偏振度变化稍微大些.

表2　碰撞次数对偏振度的影响

3结论

探究偏振光在大气气溶胶中的传输变化特性发现：随着波长的增大，相同气溶胶对偏振光的消偏特性有增强的趋势；气溶胶粒径，对线偏、45°线偏的影响表现不明显，对圆偏振光的影响稍微大些；碰撞次数，对入射光为线偏和圆偏的出射偏振度影响不明显，对入射光为45°线偏出射偏振度变化稍微大些.笔者的模拟实验结果为偏振光在大气中的传输问题进一步研究提供了一定的帮助.当然也存在许多后续工作需做更进一步研究的地方，例如在给出了偏振度变化的情况，具体考虑出射光的四个斯托克斯矢量的变化问题.总之，偏振光在大气气溶胶中的传输问题是一个及其复杂的系统，要完全研究透偏振光波长、大气气溶胶粒径以及浓度对其偏振特性的影响等仍需做更多的研究.

参考文献：

[1]袁兴起.群体粒子场激光侧向散射性质研究及建模分析[D].南京:南京理工大学,2007.

[2]陈刚.光散射法测量颗粒尺寸和浓度的实验研究[D].西安:西安电子科技大学,2007.

[3]张华伟杨俊才.偏振光蒙特卡罗大气传输模型及其应用研究[D].长沙：国防科学技术大学,2010.

[4]OLEG S, UGOLNIKOVOV, POSTYLYAKOV, et al. Effects of multiple scattering and atmospheric aerosol on the polarization of the journal of quantitative[J].Spectroscopy and Radiative Transfer,2004,88(3):233-241.

[5]杨利红,柯熙政,马冬冬.偏振激光在大气传输中的退偏研究[J].光电工程,2008,35(11):62-67.

[6]覃彬.基于Mie散射天空偏振光特性的研究[D].大连:大连理工大学,2013.

[7]陈璐玲,杨晖,郑刚,等.动态线偏振光散射纳米颗粒粒度测量法的研究与分析[J].光学仪器,2010,32(5):1-5.

[8]叶伏秋,群体粒子散射光偏振特性的研究[J].应用光学,2004,25(2):22-24.

[9]郝增周,龚芳,潘德炉,等.沙尘气溶胶粒子群的散射和偏振特性[J].光学学报,2012,32(1):8-15.

[10]张倩倩,高隽,徐小红,等.多粒子散射的偏振传输特性分析[J].中国激光,2012,39(12):280-287.

[11]汲云涛,任中京.Mie理论在静态光散射粒度测量的应用下限研究[J].中国粉体技术,2005(6):14-16.

[12]BOHREN C F, HUFFMAN D R. Absorption and scattering of light by small particles[M]. Weinheim: Wiley-VCH,1998:35-50.

[13]陈军,尤政,周兆英.激光散射理论及其在计量测试中的应用[J].激光技术,1996,20(6):359-365.

[14]李小川,廖云.蓝绿激光在海水中的散射特性及其退偏研究[D].成都：电子科技大学,2006.

[15]程成,吴永久.常用光纤材料基底中CdSe,CdS和CdTe量子点的光谱吸收截面和散射截面[J].浙江工业大学学报,2013,41(1):110-115.

[16]WANG Lihong, JACQUES L, ZHEN Liqiong. MCML- Monte Carlo modeling of light transport in multi layered tissues[J]. Methods and Program in Biomedicine,1995,47(2):131-146.

[17]蒋哲,陈良富,王中挺.细粒子气溶胶光学厚度和谱分布偏振的反演[J].地球信息科学学报,2012,14(4):460-464.

(责任编辑：陈石平)

Study on the transmission characteristics of the polarized light in the

atmosphere based on Monte Carlo method

HU Laigui, XIANG Zhoupeng, SUI Chenghua, YAN Bo, CHEN Naibo

(College of Science, Zhejiang University of Technology, Hangzhou 310023, China)

Abstract:Due to potential application value of polarization characteristics of light transmitting in the atmosphere, it has attracted a great deal of research interest. In this paper, the Stokes vector is used to describe photon polarization states, the Mie theory recursive formula is used to calculate scattering phase function, refused algorithm is used to select the scattering angle, and the Monte Carlo method is used to simulate the situation of Photon scattering in the atmosphere. For most ubiquitous forward scattering phenomenon, there are three kinds of polarized lights such as a horizontal polarized light with wavelength of 350 ～ 750 nm, 45° linearly polarized light and right-handed circularly polarized light. Firstly, the changes in the degree of polarization of their exit surfaces are simulated when they enter the atmosphere Secondly, when the polarized light passing through the aerosol with particle size of 1 000～ 1 500 nm, the changes in the degree of polarization of their exit surfaces are analyzed The simulation results provide some help for the study on the transmission problems of polarized light in the atmosphere.

Keywords:Monte Carlo; mie scattering;aerosol; polarized light

文章编号：1006-4303(2015)04-0416-04

中图分类号：O436.2

文献标志码：A

作者简介：胡来归(1978—)，男，浙江金华人，副教授，研究方向为光学信息的传递、处理以及有源与无源器件，E-mail:laiguihu@zjut.edu.cn.

收稿日期：2015-02-06