一个含四个圈的本原有向图的m-competition指数

宋卓蓉，高玉斌

(中北大学数学系, 山西　太原　030051)



一个含四个圈的本原有向图的m-competition指数

宋卓蓉，高玉斌

(中北大学数学系, 山西太原030051)

[摘要]对于n阶本原有向图D中任意顶点u和v,若都存在m(1≤m≤n)个不同的顶点v1,v2,…,vm∈V(D), 使得成立，则称最小正整数k为本原有向图D的m-competition指数. 本文研究了一类含有一个n长圈、三个n-2长圈的本原有向图, 确定了本原有向图的m-competition指数.

[关键词]本原有向图; m-competition指数; 圈

1预备知识

本原有向图本原指数的研究已经逐步扩展到了对本原有向图的scrambling指数的研究.本原有向图的scrambling 指数是一个新兴研究分支，也是近两年来在组合数学中较为活跃的一个研究方向，在计算机科学中具有广泛的实际应用背景.2009年,文献[2]中作者提出了本原图的scrambling指数的概念. 2010年,文献[4]将本原图的scrambling指数推广到m-competition指数，并对指数达到的上界进行了极图刻画．

设D=(V,E)是一个n阶有向图, 其中顶点集V=V(D), 弧集E=E(D)(允许有环但无重弧).一个有向图D是本原的，当且仅当存在正整数k，使得D中的任意一点u到另外一点v(v可能等于u)都存在k长途径.称满足上述条件的最小正整数k为有向图D的本原指数，记为exp(D).

设D一个n阶本原有向图,k∈Z+, 对于任意x,y∈V(D),用N+(Dk:x，y)=N+(Dk:x)∩N+(Dk:y)表示顶点x的k步外邻域.用N+(Dk:x，y)表示顶点x,y的k步公共外邻域.

定义 1[2]设D是n阶本原有向图,如果存在k∈Z+,对于D中任意顶点u和v, 都存在顶点w∈V(D),使得从u和v到w都有k长途径,满足上述条件的最小正整数k称为本原有向图D的scrambling指数,记为k(D).

2主要结论及证明

设n≥7,n为奇数,本文主要研究了一个含一个n圈和3个n-2圈的n阶本原有向图，计算得到了此类本原有向图的m-competition指数.

定理1设D是一个n阶本原有向图,如图1所示,其中n≥7,n为奇数,则对任意1≤m≤n:

证明由本原有向图D，可以得到有向图Dn-2和Dn.

图1　有向图D

1)m=1

V(Dn)={v1,v2,…,vn}

图2　有向图Dn

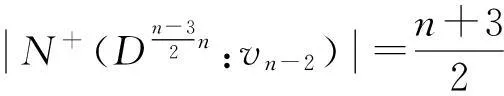
观察图D，顶点v1,v2,…,vn-4,vn-1,vn构成一个n-2圈，不妨将这个n-2圈记为C. 在图Dn中，令M=Dn[{v1,v2,…,vn-4,vn-1,vn}]，M为Dn的一个导出子图.其中

V(M)={v1,v2,…,vn-4,vn-1,vn},

E(M)=E(Dn)-{(vn-4,vn-2),(vn-2,vn),(vn-5,vn-3),(vn-3,vn-1)}

在图M中,对任意vi、vj∈V(M),因为

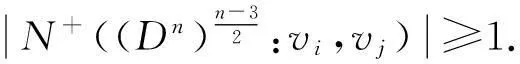
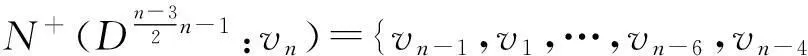
故

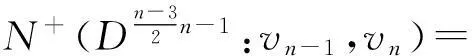
所以

2)m为奇数，3≤m≤n

在Dn-2中,

图3　有向图Dn-2

V(Dn-2)={v1,v2,…,vn}

∪{(vn-3,vn-1),(vn-2,vn)}

故对任意u,v∈V(D),均有

所以

={vn-4,…,vn-m+2,vn-m}.

故

∪{vn-m,…,vn-1}.

所以

3)m为偶数，2≤m≤n-1

故对任意u、v∈V(D),均有

所以

={vn-5,vn-7,…,vn-m-2}.

故

{vn-m-1,…,vn-5}

所以

定理得证.

[参考文献]

[1]BrualdiRA,RyserHJ.Combinatorialmatrixtheory[M].Cambridgc：CambridgeUniversityPress,1991.

[2]AkelbekM,KirklandS.Coefficientsofergodicityandthescramblingindex[J].LinearAlgebraanditsApplications, 2009, 430:1099-1110.

[3]HuangYF,LiuBL.Generalizedscramblingindicesofaprimitivedigraphs[J].LinearAlgebraanditsApplications, 2010, 433:1798-1808.

[4]KimHK.Generalizedcompetitionindexofaprimitivedigraph[J].LinearAlgebraanditsApplications, 2010, 433: 72-79.

[5]GaoYB,ShaoYL.Thescramblingindicesofprimitivedigraphswithexactlytwocycles[J].ArsCombination, 2013, 108:505-513.

[6]ShaoYL,GaoYB.Them-competitionindicesofsymmetricprimitivedigraphswithloop[J].ArsCombination, 2013, 108: 217-223.

[7]KimHK,PankSG.Aboundofgeneralizedcompetitionindexofaprimitivedigraph[J].LinearAlgebraanditsApplications, 2012, 436: 86-98.

[8]KimHK,LeeSH.Generalizedcompetitionindicesofsymmetricprimitivedigraphs[J].DiscreteAppliedMathematics， 2012, 160: 1583-1590.

(责任编辑穆刚)

The m-competition index of a primitive digraph with four cycles

SONG Zhuorong, GAO Yubin

(Department of Mathematics, North University of China, Taiyuan Shanxi 030051, China)

Abstract：For positive integers m and n with 1≤m≤n, the m-competition index of a primitive digraph D of order n is the smallest positive integer k such that for every pair of vertices u and v, if there is m distinct vertices v1,v2,…,vm∈V(D) such that there are walks of length k from u to viand from v to vifor 1≤i≤m. In this paper, the m-competition indices of a primitive digraph with one n-cycle and three (n-2)-cycles were studied and the m-competition index of this primitive digraph was determined.

Key words：primitive digraph; m-competition index; cycle

[中图分类号]O157.5

[文献标志码]A

[文章编号]1673-8004(2015)05-0018-04

[通讯作者]高玉斌(1962—)，男，山西忻州人，教授，博士生导师.

[作者简介]宋卓蓉(1990— )，女，山西长治人，在读研究生，主要从事组合数学方面的研究.

[基金项目]国家自然科学基金项目(11071227).

[收稿日期]2015-03-12