基于有限元分析的套管悬挂器颈部优化设计
刘 亮,张铁军,李朝明,刘 敏,邓德兵,涂铭旌
(1.重庆文理学院新材料技术研究院, 重庆 永川 402160; 2.重庆新泰机械有限责任公司, 重庆 永川 402160;3.重庆理工大学材料科学与工程学院, 重庆 巴南 400054)
基于有限元分析的套管悬挂器颈部优化设计
刘亮1,2,3,张铁军1,李朝明2,刘敏2,邓德兵2,涂铭旌1
(1.重庆文理学院新材料技术研究院, 重庆永川402160; 2.重庆新泰机械有限责任公司, 重庆永川402160;3.重庆理工大学材料科学与工程学院, 重庆巴南400054)
[摘要]心轴式套管悬挂器是石油井口中的关键设备,其颈部在工作和试压时分别承受内压和外压的作用.由于受到悬挂套管管径和连接法兰尺寸限制,悬挂器颈部壁厚较薄,因此,需对套管悬挂器颈部进行强度计算和有限元分析,验证其安全性.文章以Φ232.5 mm心轴式悬挂器为例,运用ASME标准分别计算颈部所能承受的内压和外压,并用ANSYS有限元分析计算,分别就承受内压和外压或者内外压都承受时颈部的所能承受的最高压力,从而获得经济、合理的壁厚值,并提出工程应用过程中避免颈部失效的方法.
[关键词]套管悬挂器;强度分析;ANSYS;优化设计
心轴式套管悬挂器安装在套管头内,通过各种螺纹连接套管并悬挂套管柱,其颈部与图1上面四通的下端形成副密封,并与密封钢圈和套管头组成一个密闭的环形空间,通过井口装置上的试压孔来检测套管悬挂器密封、套管副密封以及密封钢圈的密封性能,对保障井口装置安全使用至关重要.当套管悬挂器密封失效时,会耽误完井时间,并在井口无控制的状态下处理井口和重复拆装采油井口装置,增加井控作业的风险.
由于受到悬挂套管管径和连接法兰尺寸限制,悬挂器颈部壁厚受限.如何选取最佳的套管壁厚单凭经验和强度计算难以确定,而这方面的研究报道也较少.本文以Φ232.5套管悬挂器为例,对其进行强度计算和有限元分析.由图1套管悬挂器的安装图可知,套管悬挂器Φ232.5颈部可以看作一个圆柱壳,不会承受轴向载荷,仅承受内外压力的径向作用.Φ232.5心轴式套管悬挂器,选用30 CrMo材料,材料等级按API 6A中75 K材质设计、制造、验收,抗拉强度≥655 MPa,屈服强度≥517 MPa.现分别用ASME计算公式和ANSYS进行分析.
1圆柱壳的强度设计
按照API 6A规范分别进行限定,ST为静水压试验压力下的最大许用的总体一次薄膜应力强度,Sm为额定压力下的设计应力强度:
Sm=2/3SY
(1)
ST=5/6SY
(2)
式中,SY为材料规定的最低屈服强度,SY=517 MPa,Sm=2/3,SY=344.6 MPa,ST=5/6,SY=429.11 MPa
按照颈部壁厚设计,以美国 ASME Ⅷ-Ⅱ进行分析设计.所列公式以圆柱壳承受的内压或外压为基础.
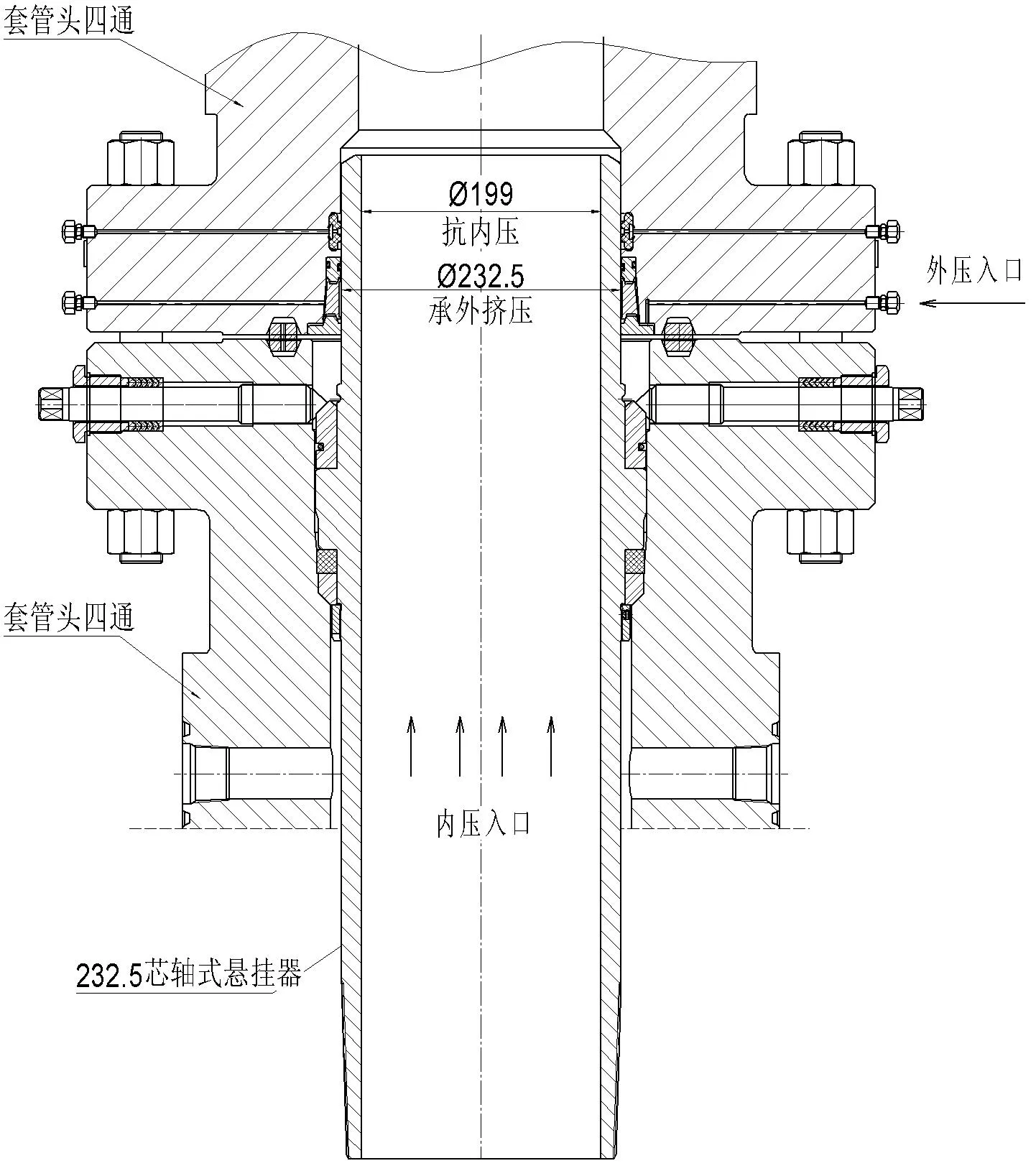
图1 套管悬挂器安装示意图
1.1 抗内压强度计算
从套管悬挂器颈部结构可以看出,其壁厚计算遵循薄壁原则,壁厚最小需要厚度应采用公式(3)确定.通过换算,在壁厚确定的情况下可以算出颈部能承受的最大内压.
(3)
实际壁厚为
t=(DW-Dn)/2 =16.75 mm
(4)
式中,DW为心轴式悬挂器颈部外径,DW=232.5 mm;Dn为心轴式悬挂器颈部内径, Dn=199 mm;E为焊接接头系数,悬挂器为整体锻造,取数值1.
通过计算,可以知道悬挂器颈部所能承受的最大内压P=53 MPa.
1.2 抗外压强度计算
根据ASME的叙述,圆柱壳体承载外压所需要的壁厚计算由公式(5)~(10)确定,假定初始厚度t=16.75 mm为油管悬挂器颈部最薄处的设计壁厚,无支撑长度L=153 mm,即悬挂器顶端无支撑部位.
计算预期的弹性失稳应力Fhe为:

(5)
式中,Ey是设计温度为-29~180 ℃时的弹性模量,查ASME第Ⅱ卷,30 CrMo材质在121 ℃时为194 000 MPa;Ch为应力系数,取决于壳体参数MZ,表达式为
(6)
式中,R0表示容器的外半径,即悬挂器承受外压处最小外半径,取值为116 mm.当1.5≤MZ≤13时,有
(7)
计算预期的失稳应力Fic值为:
Fhe/SY= 5.144 362
(8)
此时,SY= 517 Mpa.当Fhe/SY≥2.439时,Fic=SY= 517 MPa.
计算设计系数FS值:由于Fic=SY,可得FS= 1.667.
计算许用外压Pa值:
Fha=Fic/FS= 310.138
(9)
Pa=2Fha(t/D0) = 44.686 55
(10)
通过计算,可以知道悬挂器颈部所能承受的最大外压Pa=45 MPa.该悬挂器抗内压能力53 MPa,抗外挤压能力45 MPa,该值是在设计系数为1.6时的结果.若考虑瞬间承压,可适当降低设计系数,如设计系数选1时,抗外挤压能力可达72 MPa.
2颈部模型的建立及计算
由于只需要计算该段圆管抵抗内外压作用的强度,内外压强载荷是通过流体作用在管壁上的,是均匀作用在圆管周围.因此,可以在该段取一截面做强度分析,就可以知道圆管承受内外压强度的能力.圆管截面形状是均匀的圆环,作用在其上面的载荷是轴对称的,因此该问题是一轴对称平面问题.在ANSYS中建模计算时,为了提高计算效率,取圆环的1/4来求解即可.
2.1 第一种材料的求解
由于在计算时并不知道圆管内部和外部的压强,这里结合工程实际,分3种情况讨论,分别计算出各种情况下对应的应力分布图,从而确定相应的安全系数,便于实际工程参考.
第一种悬挂器材料为30 CrMo,其机械性能为抗拉强度Rm≥655 MPa;屈服强度Rel≥517 MPa ; 断面收缩率A≥17﹪;延伸率Z≥35﹪.在ANSYS分析时,选取平面单元solid Quad 4node 42 ,查得30 CrMo的材料属性值E=2.11×1011,泊松比υ=0.279.
2.1.1第一种情况——仅承受外压
1)当外压为65 MPa时,计算得到应力分布(图2)和位移分布(图3).
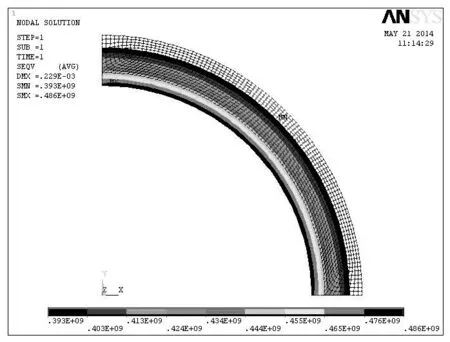
图2 外压为65 MPa时的应力分布图

图3 外压为65 MPa时的应变分布图
从图2可以看出,这种情况下最大应力为486 MPa,若以该应力为最大许用应力,则此时的安全系数=517÷486=1.06.
2)当外压为55 MPa时,计算得到应力分布如图4所示.
从图4可以看出,在外压为55 MPa时,最大应力为411 MPa,若以该应力为最大许用应力,则安全系数=517÷411=1.26.

图4 外压为55 MPa时的应力分布图
在该段圆管只承受外压的情况下,要保证圆管不发生塑性变形,其外压不得大于65 MPa.若要取常用的安全系数在1.2左右,则外部压强不得大于55 MPa.此外,我们对外部压强在60 MPa的情况做计算,最大应力为449 MPa,安全系数为517÷449=1.15.
2.1.2第二种情况——仅承受内压
1)当内压为70 MPa时,计算得到应力分布(图5)和应变分布(图6).

图5 内压为70 MPa时的应力分布

图6 内压为70 MPa时的应变分布
由图5可以看出,此时的最大应力为492 MPa,若以该最大应力作为许用应力,则安全系数=517÷492=1.05.
2)当内压为60 MPa时,计算得到其应力分布如图7所示.

图7 内压为60 MPa时的应力分布
由图7可以看出,这种情况下最大应力为422 MPa,则对应的安全系数为517÷422=1.23.由此得出结论:在该段圆管只承受内部压强作用时,为了保证其不发生塑性变形,则应使内部压强不得超过70 MPa.若要使安全系数在1.2左右,应使内部压力不能超过60 MPa.
2.1.3第三种情况——同时承受内压外压
1)当外压为100 MPa,内压为100 MPa,计算得到其应力分布如图8所示.
由图8可以看出,此时的最大应力为100 MPa,是十分安全的.
2)外压为100 MPa,内压为70 MPa,计算得到其应力分布如图9所示.

图9 在外压为100 MPa、内压为70 MPa时的应力分布
由图9可以看出,此时的最大应力为267 MPa,若以此最大应力作为许用应力,则安全系数=517÷267=1.94.
3)外压为100 MPa,内压为40 MPa,计算得到应力分布如图10所示.
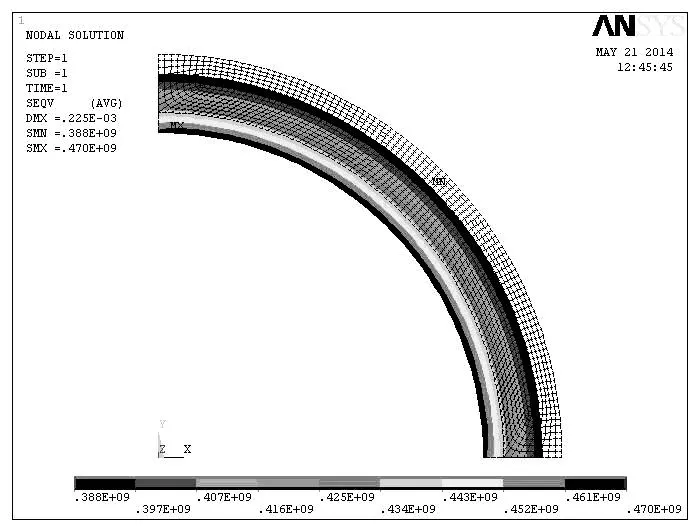
图10 在外压为100 MPa和内压为40 MPa时的应力分布图
由图10可以看出,此时的最大应力为470 MPa,对应的安全系数=517÷470=1.1
4)外压为70 MPa,内压为5 MPa,计算得到其应力分布如图11所示.
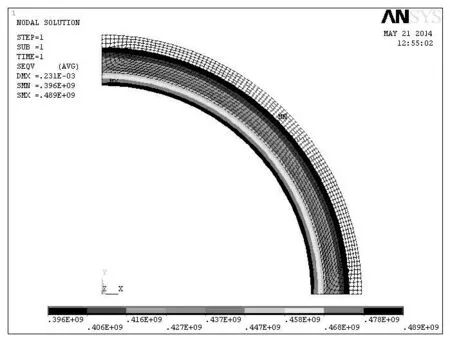
图11 在外压为70 MPa、内压为5 MPa时的应力分布图
由图10 可以看出,此时的最大应力为489 MPa,对应的安全系数=517÷489=1.06.
由以上分析得知,在该段圆管同时受到内压和外压作用时,若外部试压达到了100 MPa,则内部压强应不小于40 MPa,否则会引起塑性变形.在外部试压达到70 MPa时,内部压强应不小于5 MPa.
2.2 第二种材料的求解
同第一种材料求解的过程一样,在ANSYS中设定相关参数,并建模计算,该材料的相关属性为:Rm≥1034 MPa;Rel≥827 MPa;A≥20﹪;Z≥35﹪.同样分为3种情况讨论.
第二种材料计算的结论:当其在单独承受外压时,为了保证其不发生塑性变形,应使外部压强不大于100 MPa;当其只承受内部压强作用时,为了保证其不发生塑性变形,应使得内部压强不得大于110 MPa,同时承受内外压时,是比较安全的.
3结论
通过以上ASME设计计算和ANSYS有限元分析表明,原始方案选用的材料与套管悬挂器颈部壁厚设计不能满足设计压力要求;选用Rm≥1 034 MPa、Rel≥827 MPa的高强度钢可以提高心轴套管悬挂器颈部的抗内压和抗外压能力;套管悬挂器选用低强度的材料试压时需要反方向施加平衡压.
[参考文献]
[1]张秀辉,胡仁喜. ANSYS 14.0有限元分析从入门到精通[M]. 北京:机械工业出版社,2013:113-118.
[2]杨赟达,刘绘新,奚志雄,等. 套管悬挂器抗内压结构安全性分析[J]. 石油矿场机械,2014: 43(2):75-78.
[3]张梦华. 套管悬挂器密封失效原因及对策分析[J]. 油气井测试,2011,20(3):47-48.
[4] American Petroleum Institute. API SPEC 6A 20th-2010, specification for wellhead and christmas tree equipment[S]. Washington:API Publishing Services, 2010:28.
[5]American Society of Mechanical Engineers. ASME-BPVC-Ⅷ-2-2004, rules for construction of pressure vessels, division 2-alternative rules [S]. New York, 2004:55-63.
(责任编辑吴强)
Strength analysis and optimization design for casing hanger neck based on ANSYS
LIU Liang1,2,3, ZHANG Tiejun1, LI Chaoming2, LIU Min2, DENG Debing1,TU Mingjing1
(1. Research Institute for New Materials Technology, Chongqing University of Arts and Sciences , Yongchuan Chongqing 402160,China;
2. Chongqing Xintai Machinery Co., Ltd, Yongchuan Chongqing 402160, China;
3. College of Materials Science and Engineering, Chongqing University of Technology, Ba’nan Chongqing 400054, China)
Abstract:Spindle casing hanger is a key part in oil wellhead. Its neck sustains internal and external pressure in working condition and pressure test, respectively. Limited to the suspension bushing diameter and connecting flange size, hanger neck is thin in the wall thickness. Therefore, the strength calculation and the finite element method for the casing hanger neck are applied to ensure the safety of products. Taking the 232.5 mm spindle type hanger as an example, the use of ASME standard calculate neck can withstand the internal and external pressure. By using ANSYS finite element analysis and calculation, respectively under internal and external pressure or pressure inside and outside all under the neck can withstand the high pressure, and achieve the economic and reasonable wall thickness value. The method was put forward to avoid the neck failure in the process of engineering application.
Key words:casing hanger; strength analysis; ANSYS; optimization design
[中图分类号]U463
[文献标志码]A
[文章编号]1673-8004(2015)05-0059-05
[通讯作者]张铁军(1965—),男,黑龙江哈尔滨人,副教授,高级工程师,工学博士,主要从事失效分析、冶金熔炼方面的研究.
[作者简介]刘亮(1981—),男,湖南衡东人,工程师,工程硕士,主要从事金属材料、石油机械方面的研究.
[基金项目]重庆市永川区自然科学基金项目(Ycstc,2013nc8005);重庆文理学院科研项目(R2012RCJ19).
[收稿日期]2015-03-14

