精梳机分离罗拉传动机构的平衡研究

精梳机分离罗拉传动机构的平衡研究

李留涛1， 任家智1， 贾国欣2

(1.中原工学院； 2.河南工程学院， 郑州 450007)

摘要：使用质量—加速度法以及机构动力学分析方法，在原有精梳机分离罗拉传动机构数学建模的基础上，运用Solidworks三维建模技术、Adams虚拟样机仿真技术和Matlab计算机编程技术对精梳机分离罗拉传动机构的振动进行研究，探讨了该机构在运动过程中单个构件惯性力的变化规律以及在机构总惯性力中所占的比重，并比较了机构在优化前后惯性力的变化情况。研究表明：对分离罗拉传动机构的平衡优化，可以使机构的振动降低27%以上，有利于提高精梳机的速度和降低能源的消耗。

关键词：分离罗拉传动机构；振动；惯性力；平衡优化

中图分类号：TS112.2

文献标志码：A

DOI:10.3969/j.issn.1671-6906.2015.03.006

Abstract:Using the method of quality-acceleration and dynamics analysis, based on the modeling analysis of the existing detaching roller transmission mechanism of comber, the Solidworks 3 d modeling technology, Adams virtual prototype technology and MATLAB computer programming technology were used in studying detaching roller transmission mechanism of combing machine, the individual components of inertial force and the proportion in the total inertia force of the mechanism were discussed, and the changes of the institutions in the inertial force were compared before and after optimizing. The research results show: the balance optimization of detaching roller transmission mechanism can reduce the vibration of the institutions and more than 27% vibration is reduced, and improve the speed of combing machine and reduce the consumption of energy.

收稿日期：2014-12-11

基金项目：纺织工业协会科技指导性项目(2012024)

作者简介：李铬(1960-)，男，河南内黄人，教授。

文章编号：1671-6906(2015)03-0034-03

为完成精梳棉网的搭接及输出，精梳机的分离罗拉必须实现周期性“倒转→顺转→基本静止”的运动，因此，精梳机的分离罗拉传动机构大多采用了将平面连杆机构与差动轮系结合的传动形式，其中平面连杆机构为变速传动部分，差动轮系为恒速传动部分，二者的运动经过合成之后最终传递给分离罗拉，使分离罗拉做周期性“倒转→顺转→基本静止”的运动。

在平面连杆机构中，由于构件的数量较多，多数构件呈不规则形状且为非匀速运动，故在机构运动过程中产生了较大的振动，加剧了构件的磨损，缩短了相关构件的使用寿命，阻碍了精梳机速度的提高。因此，研究分离罗拉传动机构的振动情况，找出惯性力变化规律，并在此基础上对机构进行平衡优化，对于降低精梳机的振动具有重要意义[1-3]。

本文运用质量—加速度法以及机构动力学分析方法，在原有精梳机分离罗拉传动机构数学建模的基础上，运用Solidworks三维建模技术、Adams虚拟样机仿真技术和Matlab计算机编程技术对精梳机分离罗拉传动机构的振动进行研究，探讨了该机构在运动过程中单个构件惯性力的变化规律以及其振动产生的惯性力在机构总惯性力中所占的比重，并比较了机构在优化前后惯性力的变化情况，为精梳机速度的提高提供了理论支撑和解决途径。

1分离罗拉传动机构

图1所示为分离罗拉传动机构连杆传动部分，其中O为锡林轴，O1为偏心套旋转中心，O2为钳板摆轴中心，O3为差动臂中心。当锡林轴O匀速回转时，通过定时调节盘OA、连杆AB带动偏心套O1B做变速圆周运动。在偏心套O1B上活套有摆动臂ECD，当偏心套做圆周运动时，摆动臂ECD在摇杆O2D的约束下做变速运动；与E点铰接的连杆EF，带动首轮摆臂FO3(摇杆结合件)做周期性的摆动，即O3轴做周期性的正反向运动。

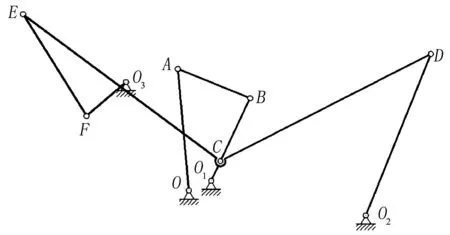
图1　分离罗拉传动机构连杆传动部分

分离罗拉传动机构轮系传动部分如图2所示。

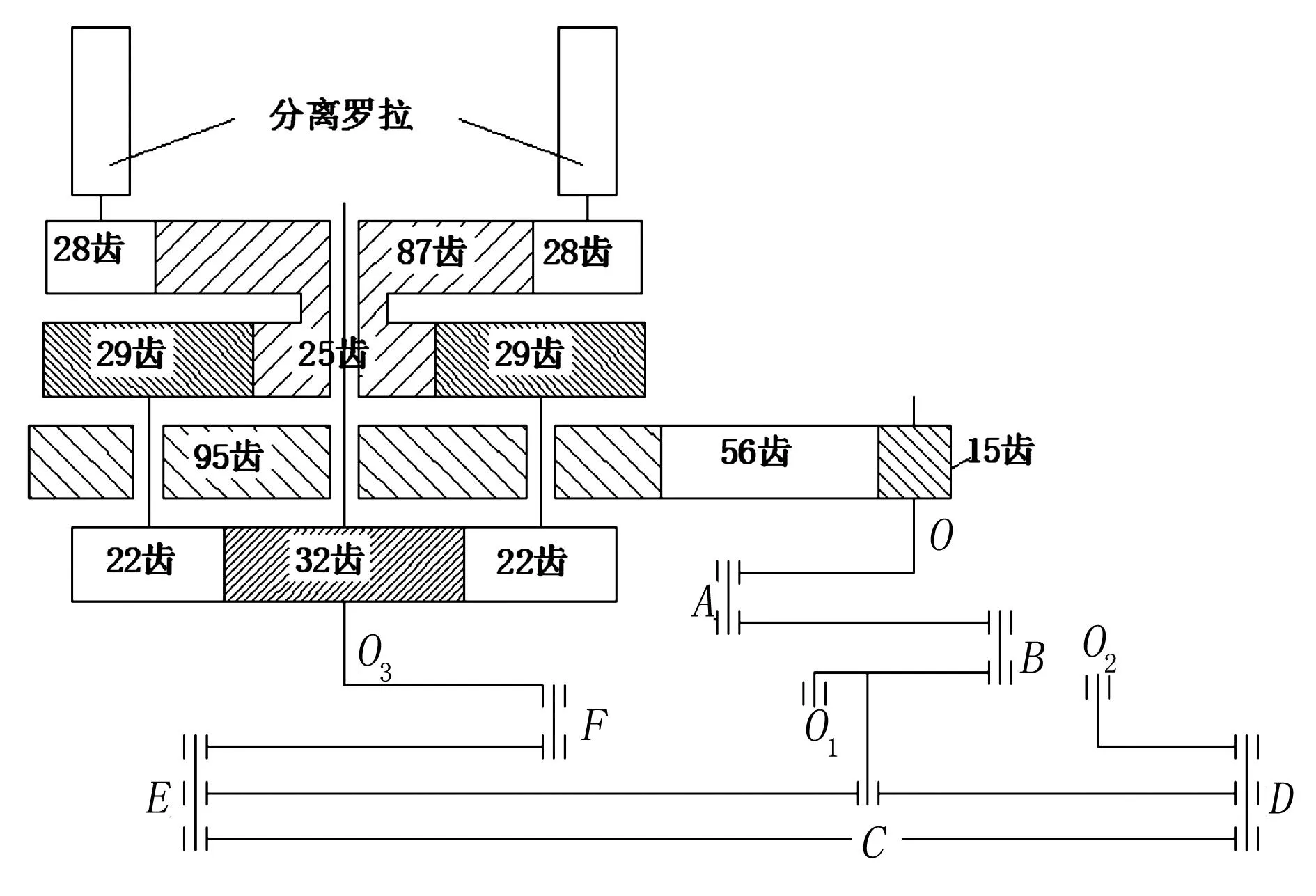
图2　分离罗拉传动机构轮系传动部分

图2中O3轴做周期性正反向运动，即差动轮系中的32齿首轮做正反向运动。在32齿齿轮轴O3上活套一个95齿齿轮，该齿轮为差动轮系的差动臂。安装在锡林轴O上的15齿齿轮，通过56齿过桥齿轮将恒速运动传递给95齿齿轮，由95齿齿轮输入行星轮系；由行星轮系将平面连杆机构传来的变速运动与锡林轴传来的恒速运动合成后，经过25齿、87齿、28齿齿轮传给分离罗拉，使分离罗拉做周期性“倒转→顺转→基本静止”的运动[4-7]。

2分离罗拉传动机构的惯性力

根据达朗贝尔原理，由各运动构件惯性力构成的惯性力系与由各构件构成的外力系组成一平衡力系，即惯性力与机构的振动力大小相等。为了掌握分离罗拉传动机构惯性力的变化规律，在对分离罗拉传动机构进行Solidworks三维建模的基础上，利用Adams虚拟样机仿真软件对该模型进行动力学分析。

根据分离罗拉传动机构中各个构件的实际尺寸，利用Solidworks三维建模软件分别绘制各个构件的实物模型，并在该软件中进行装配，然后导入Adams虚拟样机仿真软件中进行仿真。利用三维建模软件Solidworks建立的分离罗拉传动机构实物模型如图3所示。

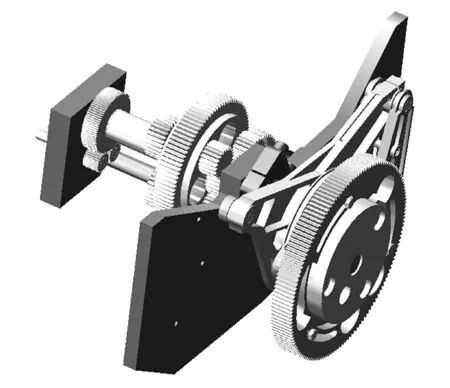
图3　分离罗拉传动机构三维实物模型

设置仿真时间为50 s，步数为10 000，精梳机速度为400钳次/min。分离罗拉传动机构中单个构件惯性力及总惯性力的仿真结果如表1所示。

表1　分离罗拉传动机构单个构件惯性力及机构总惯性力　N

以单个构件产生的惯性力和总惯性力的最大值为衡量指标，对表1中的数据进行分析可知：定时调节盘、连杆AB、偏心套、摆动臂、连杆EF、摇杆、摇杆结合件产生的惯性力占总惯性力的比重依次为：0.73%、8.01%、36.87%、38.55%、5.72%、8.75%、1.37%。可见，偏心套和摆动臂产生的惯性力在总惯性力中所占的比例远远超过其他构件惯性力所占的比例。因此，减小偏心套和摆动臂产生的惯性力可以有效地降低整个机构的惯性力，有利于提高机器的运转速度和减少整个机构的振动。

3分离罗拉传动机构的平衡优化

3.1分离罗拉传动机构的平衡分析

图4所示为利用质量-加速度法对分离罗拉传动机构进行平衡分析的原理图，其中mi(i=1～7)为机构中各个构件的质量，li(i=1～7)为图中相应构件的长度，(pi,qi)(i=1～7) 为构件的质心在相应局部坐标系中的坐标位置。

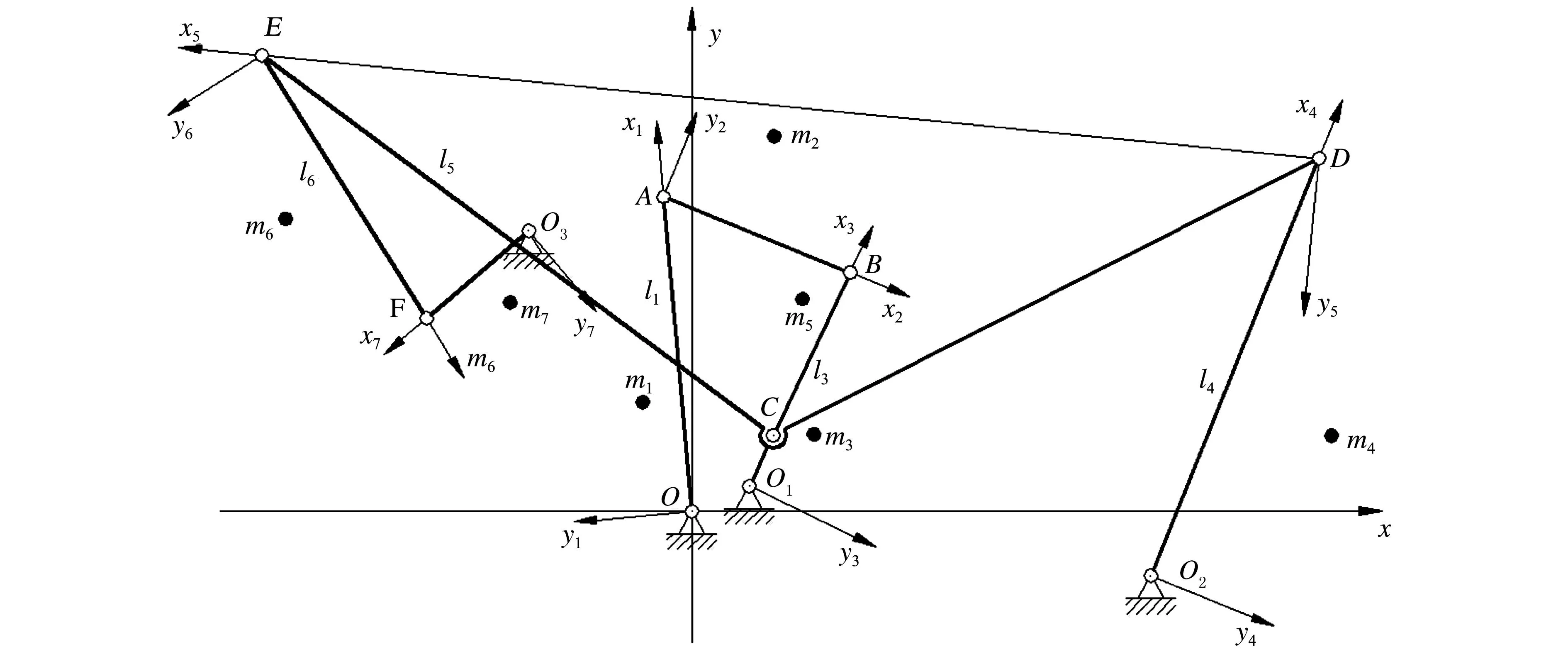
图4　分离罗拉传动机构平衡原理

根据文献[8-10]可得到机构中各个构件惯性力的矢量方程表达式。定时调节盘、连杆AB、偏心套、摇杆、摆动臂、连杆EF、摇杆结合件的惯性力矢量方程表达式分别为：

F1=-(M1O1·a1O1+M1O2·a1O2+M1A1·a1A1

+M1A2·a1A2)

(1)

F2=-(M2A1·a2A1+M2A2·a2A2+M2B1·a2B1

+M2B2·a2B2)

(2)

F3=-(M3O11 ·a3O11 +M3O12 ·a3O12 +M3B1·a3B1

+M3B2·a3B2)

(3)

F4=-(M4O21 ·a4O21 +M4O22 ·a4O22 +M4D1·a4D1

+M4D2·a4D2)

(4)

F5=-(M5C1·a5C1+M5C2·a5C2+M5E1·a5E1

+M5E2·a5E2)

(5)

F6=-(M6E1·a6E1+M6E2·a6E2+M6F1·a6F1

+M6F2·a6F2)

(6)

F7=-(M7O31 ·a7O31 +M7O32 ·a7O32 +M7F1·a7F1

+M7F2·a7F2)

(7)

其中：Mjpi与构件质量有关，称为构件j在p(p=u、v)点的第i(i=1、2)个质量参数，u、v为构件的运动副；ajpi与时间有关，称为构件j在p(p=u、v)点的第i(i=1、2)个加速度参数。

令与机架连接处运动副的加速度为0，可得到下列等式：

a1O1=a1O2=a3O11 =a3O12 =a4O22 =a7O31 =a7O32 =0

(8)

同一个旋转副处加速度相等，根据式(1)—式(8)可得分离罗拉传动机构总惯性力矢量方程表达式为

(9)

对构件ECD进行分析，可知构件ECD上第3个运动副C的加速度与其他两个运动副E、D的加速度存在如下关系：

(10)

(11)

(12)

(13)

将式(10)—(13)代入式(9)得式(14)：

F=-{(M1A1+M2A1)a1A1+(M1A2+M2A2)a1A2+(M6F1+M7F1)a6F1+(M6F2+M7F2)a6F2+(M5E2+M6E2+

(14)

其中：(p5C,q5C)、(p5D,q5D)分别为点C、点D在构件ECD局部坐标系中的坐标参数；Mjpi具体求解如式(15)—式(18):

Mju1=mj(1-pj/lj)

(15)

Mju2=mj·qj/lj

(16)

Mjv1=mj·pj/lj

(17)

Mjv2=-mj·qj/lj

(18)

式(14)即为利用质量-加速度法得到的分离罗拉传动机构惯性力矢量方程表达式。由式(14)可知：若使分离罗拉传动机构完全平衡，则加速度前面的系数应全部为0，但由于分离罗拉传动机构中构件形状以及车头箱空间位置的限制，完全平衡只能是理论上的追求，在实际生产中无法实现，故对该机构只进行部分平衡优化。

3.2分离罗拉传动机构的平衡优化

根据对分离罗拉传动机构中各个构件惯性力的分析可知：偏心套和摆动臂产生的惯性力在机构的总惯性力中所占的比例较大，故对偏心套和摆动臂进行平衡优化可以有效地降低机构的惯性力。考虑到减小摆动臂的质量可能会影响构件的正常功能，故这里只以偏心套构件优化来对分离罗拉传动机构进行平衡优化。

以平衡后机构总惯性力F的最大值最小化作为目标函数，以偏心套正常完成所设计的功能为约束条件，对公式(14)的多变量非线性函数进行最小化从而达到优化的目的。优化前后偏心套的形状如图5所示，优化前偏心套质量为6.671 96 kg，优化后为4.655 2 kg。

根据优化结果绘制偏心套实物模型并模拟安装到分离罗拉传动机构中，利用Adams虚拟样机仿真技术对机构进行仿真分析，仿真时间设置为50 s，步数为10 000，速度分别设置为350钳次/min、400钳次/min、450钳次/min。优化前后的惯性力及惯性力减少率如表2所示。

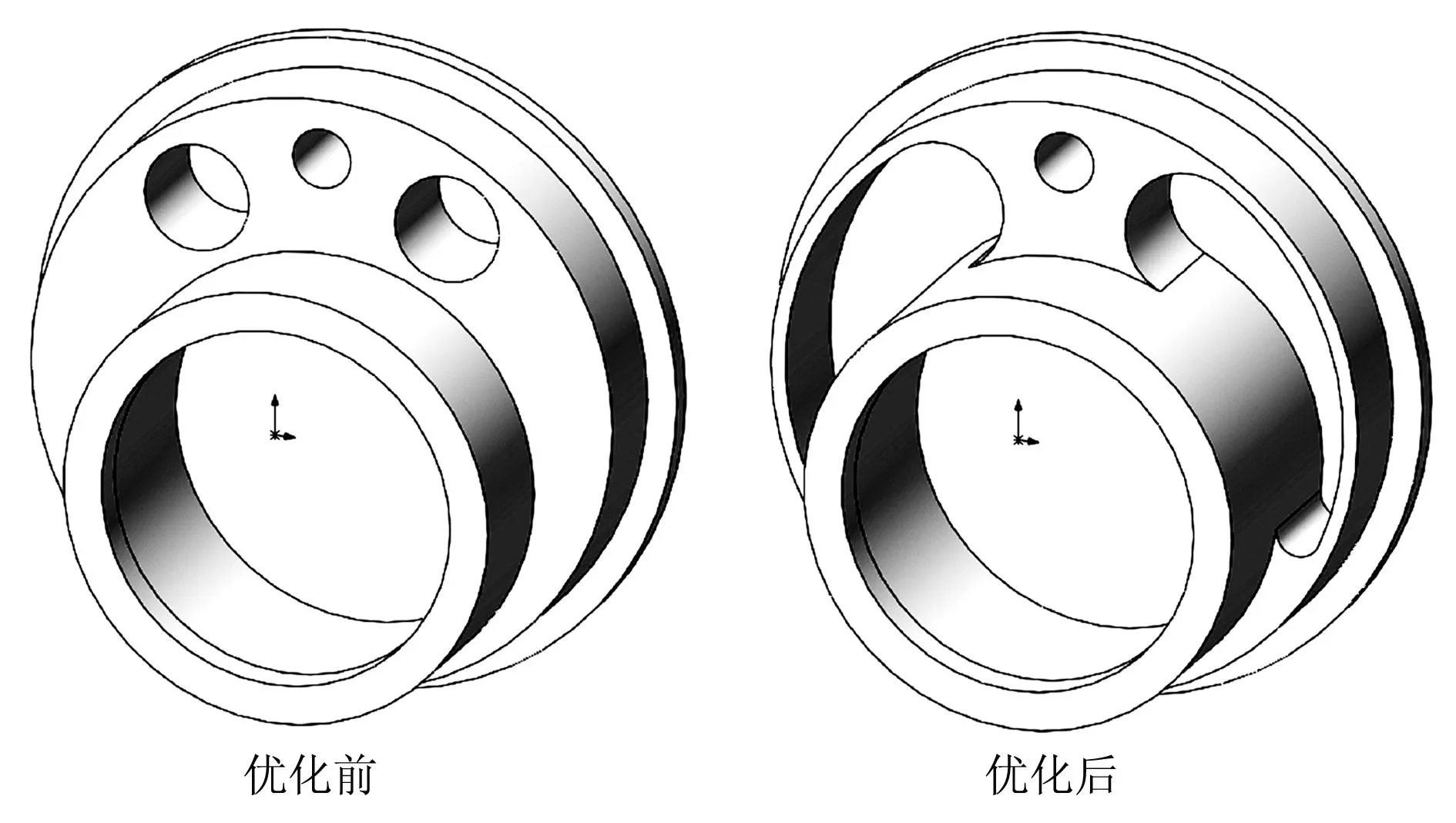
图5　优化前后偏心套的形状

特征参数速度/(钳次·min-1)350400450优化前最大值/N722.24946.671189.57最小值/N230.72300.88380.36极差/N491.52645.78809.21优化后最大值/N523.28685.06861.96最小值/N166.42217.57274.59极差/N356.86467.48587.37减少率最大值/%27.5527.6427.54最小值/%27.8727.6927.81极差/%27.3927.6127.41

由表2可知：①分离罗拉传动机构优化后比优化前的惯性力最大值减小了27.54%，最小值减小了27.69%，极差降低了27.39%；②惯性力参数的变化率均保持在恒定范围内，故当机构的优化方案确定之后，机构惯性力最大值、最小值、极差的变化率恒定，与机构的运动速度无关。

4结语

(1)精梳机在运动过程中，各个构件产生的惯性力不同，按照大小顺序依次为结合件、偏心套、摇杆、连杆AB、连杆EF、摇杆结合件、定时调节盘。对惯性力较大的构件进行平衡优化，可以有效地降低整个机构的振动，从而提高机器的运转速度。

(2)根据优化结果，对机构进行动力学仿真分析，得出了分离罗拉传动机构在不同钳次时优化前后惯性力的变化规律，即若等钳次地提高精梳机的速度，则优化前后机构惯性力的变化率相同。

(3)对分离罗拉传动机构的部分构件平衡优化，可以使机构的惯性力减少27%以上，有利于改善机构的平衡状态，该研究为精梳机速度的提高提供了理论支撑和解决途径。

参考文献：

[1]任家智,尹燕芬.棉精梳机分离罗拉传动机构分析[J].中原工学院学报, 2006, 17(4): 12—16.

[2]任家智.纺织工艺与设备[M].北京:中国纺织出版社, 2004.

[3]张立彬,杨玉广,任家智,等.降低JSFA288型精梳机噪声及振动的研究[J].棉纺织技术, 2011, 39(3): 13—15.

[4]刘国涛.现代棉纺技术基础[M]. 北京:中国纺织出版社, 1999.

[5]杜虹,韩凤萍.精梳机分离罗拉机构的设计与分析[J].郑州纺织工学院学报, 1999, 10(1): 86—89.

[6]任家智.高效能精梳技术及技术创新的探讨[J].棉纺织技术, 2001, 29(4): 12—16.

[7]任家智,郁崇文.E62型精梳机分离罗拉传动机构工艺性能研究[J].纺织学报, 2004, 25(6): 32—34.

[8]王荣,汤文成,赵春花.精梳机钳板机构的振动平衡优化[J].制造业自动化, 2009, 31(12): 101—104.

[9]王炳乐，宋立权.机构惯性力平衡的质量-加速度参数法[J].重庆建筑工程学院学报, 1988, 32: 65—72.

[10]李常青,楼梦麟,余志武,等.近似平衡多项式加速度动力显式算法[J].应用力学学报, 2011, 28(5): 475—479.

(责任编辑：姜海芹)

The Balance Study of Detaching Roller Transmission

Mechanism on Comber

LI Liu-tao1， REN Jia-zhi1， JIA Guo-xin2

(1.Zhongyuan University of Technology, Zhengzhou 450007；

2.Henan Institute of Engineering, Zhengzhou 450007, China)

Key words:detaching roller transmission mechanism；vibration；inertia force；balance optimization