三参数威布尔分布模型在系统的可靠性评估中的应用
,,
(1.西北工业大学,陕西 西安 710072;2.东方航空公司西安维修基地,陕西 西安 712000)
Estimation the System Reliability based on 3-Parameter Weibull Distribution Model
WANG Haitao1,CHEN Xing1, DUAN Feifei2
(1.Northwestern Polytechnical University,Xi’an,710072,China;2.China Eastern Xibei Maintenance Base, Xi’an 712000,China)
三参数威布尔分布模型在系统的可靠性评估中的应用
王海涛1,陈星1,段斐翡2
(1.西北工业大学,陕西 西安 710072;2.东方航空公司西安维修基地,陕西 西安 712000)
Estimation the System Reliability based on 3-Parameter Weibull Distribution Model
WANG Haitao1,CHEN Xing1, DUAN Feifei2
(1.Northwestern Polytechnical University,Xi’an,710072,China;2.China Eastern Xibei Maintenance Base, Xi’an 712000,China)
摘要:威布尔分布是目前可靠性领域内最流行的模型之一,在此,采用三参数威布尔分布模型建模,用相关系数法求得位置参数,通过最小二乘法求得形状参数和尺度参数,运用WQS软件拟合出最小二乘回归直线,得出相关的可靠性数据。并且通过对涡轮叶片可靠性分析的实例,验证了三参数威布尔模型比两参数模型拥有更高的精确度。
关键词:三参数威布尔分布;相关系数法;最小二乘法;可靠性
中图分类号:O213.2
文献标识码:A
文章编号:1001-2257(2015)03-0078-03
收稿日期:2014-12-10
Abstract:The Weibull distribution is one of the most popular models in the field of reliability. This article use the 3-parameter Weibull distribution model,get the positional parameter by using the correlation coefficient method and solve the shape parameter &scale parameter by using the least squares method. Through analysis the data of turbine fan we prove that the 3-parameter Weibull distribution has the higher accuracy than 2-parameter model. Computation is made using ‘Windchill Quality Solution 10.1 Tryout’ software.
作者简介:王海涛(1972-),男,黑龙江哈尔滨人,博士,副教授,中国航空学会会员,西北工业大学航空学院民航工程系系主任,研究方向为起落架主动控制、飞机适航等。

Key words:3-parameter weibull distribution;correlation coefficient method;least squares;reliability
0引言
在寿命数据分析中,使用最广泛的就是威布尔分布,它的主要优点是利用有限的数据样本,就能够给出精确的分析和预测结果。从产品的早期阶段、使用阶段和疲劳阶段获得的数据都可以使用它进行分析。它广泛应用于机械、化工、电气、电子和材料的失效研究。威布尔模型是研究机械零部件可靠性的最适合的模型之一。标准的威布尔分布能够拟合各种类型的寿命数据,当其形状参数分别取特定的数值时,它接近于指数分布、正态分布等分布类型。用威布尔分布可以拟合各种可靠性数据,计算产品的可靠性指标,为故障树分析、可靠性设计、可靠性预计与分配等工作提供了统计学依据。
余国林等提出了两参数威布尔分布在可靠性评估中的应用,但是两参数的威布尔分布忽略了位置参数,这意味着没有考虑产品或者系统的最低可靠性时间,与现实情况不符,并容易产生计算精度的误差。
1三参数威布尔分布建模
1.1 三参数威布尔分布函数
威布尔分布的寿命分布函数为:
(1)
t为时间;γ为位置参数;η为尺度参数;β为形状参数。
对式(1)整理得:
(2)

则式(2)可简化为:
y=ax+b
(3)
设可靠性寿命试验的样本数量为n,失效样本的寿命时间分别(顺序统计量)为t1≤t2≤…≤tn,对应的累计失效概率(经验分布函数)为F(t1)≤F(t2)≤…≤F(tn),其中到第i个产品的累计失效概率F(ti)可用中位秩算法求得,即
(4)
1.2 最大相关系数优化法


x与y间的相关系数R(x,y)为:
(5)

整理可得:
(6)
满足式(6)的γ即为所求的位置参数。
威布尔分布的可靠度函数为:
(7)
失效率函数为:
(8)
威布尔分布概率密度的平均故障时间为:
(9)
1.3 三参数威布尔分布参数求解
在工程应用中可用中位秩法计算出F(ti)后得到yi,如果(xi,yi)数据上大体沿一条直线分布,则故障时间可以用三参数威布尔分布建模,并且如果相关系数R(x,y)越大,证明数据拟合度越好,计算结果越精确。式(6)所表示的方程十分复杂,解该方程一般是通过编程,用数值解法求出位置参数,然后再通过最小二乘法或其他方法求解形状参数和尺度参数。
运用WQS软件通过实例分别应用两参数威布尔模型和三参数威布尔模型建模仿真,得出各个参数的估计值,并通过计算比较两种模型的优劣。
1.4 参数估计优劣的评价标准
对于同一个样本,若采用不同的估计方法,将得到不同的结果,为了定量表示应用不同方法,对同一试验样本进行拟合的精确程度,统计学中常用均方根误差(RMSD)和相对均方根误差(NRSME)2种评价指标。
(10)
(11)

2WQS对设备可靠性评估
2.1 数据模拟
WQS(windchill quality solutions 10.1)是一款可靠性分析软件,它拥有多个模块可以对产品或系统的可靠性做出全面的分析。运用其中的weibull分布模块对参考文献中某型号发动机涡轮叶片故障数据进行分析,具体数据如表1所示。

表1 涡轮叶片失效数据表
分别通过两参数和三参数威布尔模型建模,选取中位秩法进行仿真,通过计算机软件仿真可以得到,可靠度与时间关系图以及失效率与时间关系如图1和图2所示。

图1 可靠度与时间
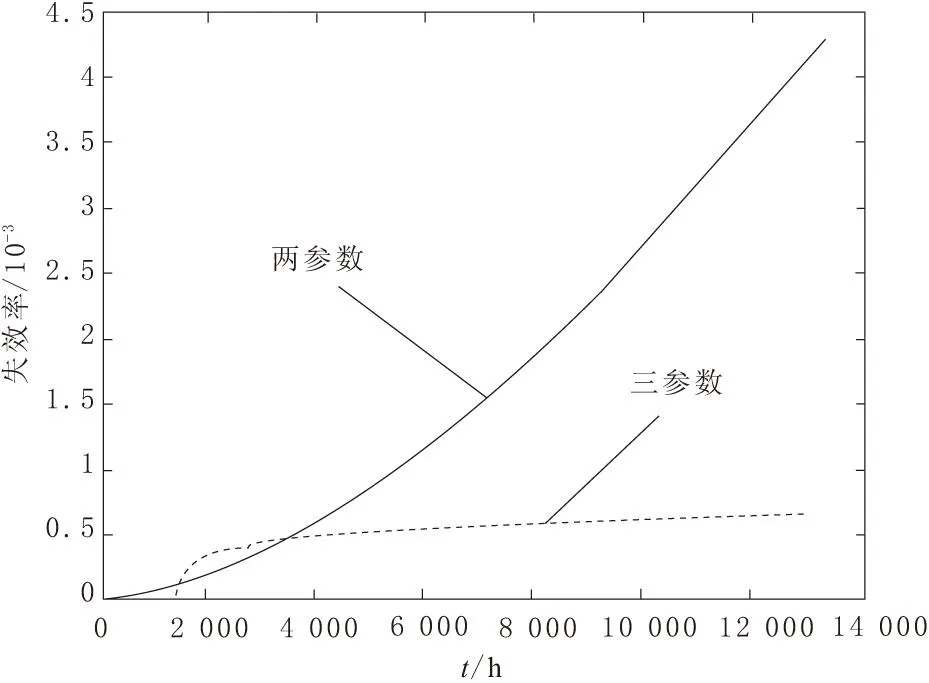
图2 失效率与时间
2.2 结果和讨论
通过计算得到对于两参数威布尔分布,形状参数β1=2.618 9,尺度参数η1=4 085.3 相关系数R(x,y)1 =0.973 3。对于三参数威布尔分布,形状参数β2=1.208 8,尺度参数η2=2 517.2,位置参数γ=1 391.4,相关性系数R(x,y)=0.987 1。其他数据如表2所示。

表2 使用不同模型的参数估计结果
从以上计算得出,三参数威布尔模型的相关系数要大于两参数的模型,而均方根误差RMSD和相对均方根误差NRMSE的值均小于两参数模型,同时从图1看出三参数模型比两参数模型的拟合度更好,由此可见,考虑了位置参数的三参数威布尔模型在实际应用中更加精确,误差更小。而从图2中可以看出,两参数威布尔分布的失效率曲线增长过快,与实际情况不符,应用后可能产生很大误差。
3结束语
用三参数威布尔分布对飞机部件的使用可靠性进行了分析,通过相关系数法计算相关参数,应用WQS可靠性分析软件验证了其在处理机械部件故障概率上可用性。通过与两参数威布尔分布的比较看出,应用三参数威布尔分布模型的计算结果更加精确,对于工程应用更有帮助。该方法还可用于飞机整机设备、发动机的可靠性评估。评估结果可直接作为可靠性监控的依据,进而实现对飞机的维修大纲和航空公司的维修方案,进行动态管理和有效控制,保持其正确、完整、有效和实用,为科学维修和新机研制提供参考。
参考文献:
[1]凌丹. 威布尔分布模型及其在机械可靠性中的应用研究. 西安:电子科技大学,2011.
[2]余国林,吴海桥,丁运亮. 威布尔分布在飞机系统使用可靠性评估中的应用. 航空维修与工程,2006(2):49-51.
[3]Hines W W, Montgomery D C. Probability and statistics in engineering and management science. New York: John Wiley&Sons, 1990.
[4]李书明,董成利,黄燕晓,等. 基于威布尔的发动机涡轮叶片寿命可靠性评估. 中国民航大学学报,2008,26(4):14-17.


