基于有限元结构动力学模型的塔架振动分析
,,,
( 许昌许继风电科技有限公司,河南 许昌 461000)
Based on the Finite Element Dynamic Model of Tower Vibration Analysis
YANG Yinkai,LU Xiaoguang,YUE Hongxuan,XU Ming
(XJ-Wind Power Technology Company,Xuchang 461000,China)
基于有限元结构动力学模型的塔架振动分析
杨银锴,卢晓光,岳红轩,许明
( 许昌许继风电科技有限公司,河南 许昌 461000)
Based on the Finite Element Dynamic Model of Tower Vibration Analysis
YANG Yinkai,LU Xiaoguang,YUE Hongxuan,XU Ming
(XJ-Wind Power Technology Company,Xuchang 461000,China)
摘要:为深入了解风机塔架的动态特性,并解决运行过程中的塔架振动问题,研究了塔架有限元动力学方程的建模方法,建立了塔架动力学方程;依据动力学方程,研究了塔架模态的求解方法,得到了塔架基础刚度、塔架质量及塔架刚度对塔架模态的影响趋势,为风机塔架制造、安装过程提供理论参考依据。并依据动力学方程,研究了塔架动力学相应的求解过程,进而设计了基于塔架激励减缓的多目标变桨控制方法,仿真和风场实验结果表明,此方法可有效减小塔架振动告警,减小风机停机次数,从而提高发电量。
关键词:塔架;有限元方法;动力学方程;振动控制;bladed仿真
中图分类号:TM614
文献标识码:A
文章编号:1001-2257(2015)03-0034-05
收稿日期:2014-08-26
Abstract:In order to deeply understand the dynamic characteristics of the wind turbine tower,and solve the problems during the operation of the vibration of the tower. Research on modeling method for tower finite element equations of dynamics,established the tower dynamics equation; based on Dynamics equations,the method to calculate the modal of the tower,tower foundation stiffness,mass and stiffness of tower tower to tower modal tendency,to provide theoretical reference for the wind turbine tower manufacture,installation process.Based on the dynamic equation,the solution procedure of tower dynamics accordingly,and then designed a variable pitch control method based on multi-objective excitation slow tower,wind farm simulation and experimental results show that this method can effectively reduce the vibration of the tower alarm,reduce wind machine downtime,and improve power capacity.
作者简介:杨银锴(1975-),男,河南许昌人,硕士,工程师,研究方向为电力系统自动化和风机控制;卢晓光(1983-),男,河南许昌人,硕士,工程师,研究方向为机电一体化。

Key words:tower;finite element method;kinetic equation;vibration control;bladed software
0引言
大型风力机塔架占风力发电机整机成本的很大比重,深入研究塔架动力学过程,是减小塔架制造材料,节约塔架制造成本的关键。在风机塔架由刚性塔架设计向柔性塔架设计转变的时代,研究塔架制造及安装对塔架动态特性的影响十分必要。控制塔架运行过程中的过大振动[3CD*25],也是进一步减小塔架材料制造用量,增加风机可利用率的关键。目前,塔架振动控制的研究大多集中于塔架加阻算法,大量学者都对此课题有深入研究,但是加阻导致的不稳定因素一直没能解决,有时甚至激起塔架的更大振动。
围绕以上需求及问题,建立了基于有限元思想的塔架动力学方程,并通过计算量较小的子空间迭代法对动力学方程进行模态分析,从而得到塔架动态特性的主要特征。利用模态分析过程,对塔架制造及安装过程中的重要因素进行假定计算,从而得出塔架制造安装过程理论依据。然后对塔架方程的响应求解研究,寻找控制塔架振动的另一个思路—塔架激励减缓方法,并设计了控制过程,对控制过程进行了仿真实验及风场实验,以验证方法的有效性及控制效果。
1塔架有限元动力学方程的建立
1.1 单元动力学方程的建立
在结构振动中,结构离散成有限个单元结构体后,单元的任意节点的位移为时间和坐标的函数,其对时间的一阶导及二阶导数,即为节点速度和节点加速度,其定义为:
设施加在单元节点上1个激励力F,在单元节点上利用虚功原理,可列写如下虚功方程,即
(1)
δ*为单元节点的假设虚应变;d*为单元节点的假设虚位移;ρ 为材料密度;υ为阻尼系数;σ为节点应力。
引入单元形状函数阵N,单元应变阵B,单元弹性阵D。
当节点划分足够细时,可以得到:d=Nδ,ε=Βδ,σ=DBδ。
则式(1)可变为:
节点应变和虚应变及应变的速度加速度都可看成常数,且虚应变为任意值,上式均成立。则可得:

令
m=∭VNTρN,
c=∭VNTυN,k=∭VBTDB,
因此,可把单元动力学方程写为:

(2)
式(2)揭示了单元节点的惯性力、阻尼力和弹性力正好与外加激励力平横,符合达朗伯原理,在此,分别用单元质量阵,单元阻尼阵和单元刚度阵命名,式(2)即为单元动力学方程。
1.2 弹性结构动力学方程的建立
设式(2)中节点局部坐标到单元统一坐标的单元坐标变换阵为T,即

(3)
(4)
利用虚功标量特性,其与坐标无关,两种坐标系惯性力虚功应相等,即
(5)

综合式(3)~式(5),并考虑虚位移是任意的,可从等式两端消去,可得:
(6)
(7)
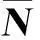
同理,统一坐标下阻尼阵可变换为:
(8)

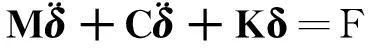
(9)
1.3 塔架模型的建立
塔架采用梁单元建模,第i个单元刚度阵和质量阵分别为:

n为单元数。
阻尼是个复杂的问题,在结构振动中,阻尼的影响相对于惯性和刚度是很小的,一般采用阻尼阵与质量阵或刚度阵的方法令:
C=aM
因材料密度ρ为正数,可以证明,上述矩阵为对称正定矩阵。以许继2 MW风机塔架数据为例,材料密度7 850 kg/m3,弹性模量2.1×1011N/m2,分41个单元,带入式(9),即可得到相应的塔架振动动力学有限元方程。
2塔架模态求法及对优化的指导
2.1 模态频率求法
当塔架做无阻尼自由振动时,式(9)变为:
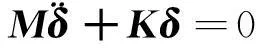
(10)
考虑简谐振动解的形式,假定式(10)的解为δ=qejot,其中q为振幅阵列,ω为固有频率阵列,t为时间。带入式(10)可得:
(11)
令λ=ω2,因q为非0向量,式(10)有解的条件为矩阵行K-λΜ列式为0,即
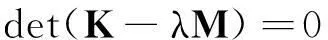
(12)
添加约束条件,使刚度阵正定,解出广义特征值λi(i=1,2…,n),即可得模态频率为:
每一个模态频率对应一个模态振型,即模态频率所对应的特征向量解,计为:
经验及大量研究结果表明,对塔架振动起决定作用的是振动的前几阶模态[6-7]。因塔架方程矩阵阶数较高,故应用雅可比方法、幂级数迭代法及反迭代的方法求解特征值问题计算过于复杂,本为选择子空间迭代的方法求取塔架的前几阶模态频率及振型。以便减小矩阵空间维度,减小迭代次数,节约计算时间,同时又能精确反应塔架的主要振动特性。
2.2 塔架制造安装对模态频率的影响
以许继2MW塔架数据为例,应用以上建立的塔架模型,塔架顶端设置为集中质量,此质量模拟叶片及机舱质量,计算中不会改变。现分别设置塔基为不同刚度,得到塔架的一阶振动模态频率如表1所示。

表1 塔架一阶模态随基础刚度的变化趋势
由表1可知,当基础刚度低于3×1010的数量级时,塔架模态频率降低很多,在做风机基础时必须注意这一特点,基础刚度要在3×1010数量级以上。设塔架基础为刚性,改变塔架材料密度,以寻找质量对塔架模态的影响,如表2所示。

表2 塔架一阶模态随塔架质量的变化趋势
由表2可知,在刚度不变时,质量的增加会导致一阶模态频率缓慢降低,但改变不大。这一结论可知道在塔架局部增加点质量的指导。
设塔架基础为刚性,改变塔架弹性模量,以寻找刚度对塔架模态的影响,如表3所示。
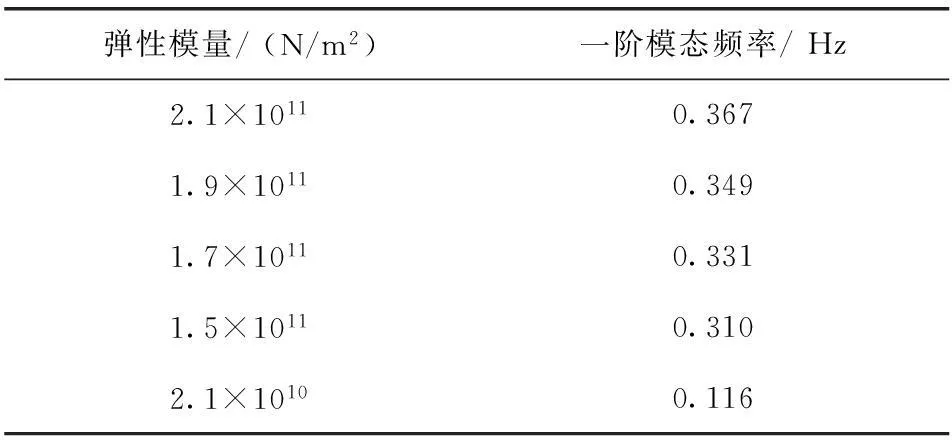
表3 塔架一阶模态随塔架刚度的变化趋势
由表3可知,刚度对塔架一阶模态影响非常大,刚度的降低一阶模态也随之快速降低。在塔架制造过程中影响刚度的因素如制造工艺和材料质量都要严格把握。
塔架的一阶模态频率要设计在风轮旋转频率的1倍频与3倍频之间,以避免共振。风轮的旋转频率1P是一个频带,本文算例风机为0.145~0.26Hz之间。以一阶模态避开1P、3P的10%计算,塔架设计一阶模态应落在0.29~0.395Hz之间。
3塔架响应分析及减振控制
3.1 振动响应求解
利用振型叠加法求解动力响应,把式(8)的位移用变量x表示,即:
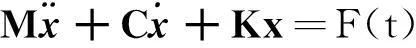
(13)
令式(13)的激励力为F(t)=Fejωt,则可假定强迫振动振幅为x=qejωt,对时间求一阶和二阶倒数,带入式(13)可得:
(14)
对于固定的ω,式(14)代表n个方程,通过解耦可,使式13变为n个单自由度方程求解。解耦过程可以利用模态振型进行。实验及实际数据表明,F(t)所激起的激励,只是激励频率较低的前几个模态振型起作主要用,对于塔架振动,前3阶模态已经包含了激励90%以上的能量。
位移x可表示为振型的函数,即
当取前m阶近似时,即
(15)
故此,式(12)可变为:
(16)
式(16)已经是对角化的解耦方程。η表示各阶模态在响应中的参与比重,即参与因子。利用式(16)可以分出m个单自由度方程,即

分别求解m个单自由度方程。带入式(15),即可得到结构响应位移。对于非周期性激励,可以用傅里叶基数展开,然后应用谐波分析,使其分解为若干频率成整数倍的简谐激励函数,即
ω为基频。
根据叠加原理,在F(t)激励下的响应等于各简谐激励单独作用的效果之和,以此可得到系统的总响应。
3.2 基于激励减缓的多目标变桨控制
风机塔架振动一般出现在变桨过程中,且为变桨角度减小的过程中,变桨时风载对叶片产生一个推力的变化。从而引入一个塔架激励的较大变化,引起塔架振动。控制塔架振动的方法可以从2个方面考虑,一是增加塔架阻尼的方法,此方法已有大量学者研究,在仿真过程中有明显的抑制振动效果,但风场应用中由于相位问题,很难取得理想效果。另一种方法即主动减小塔架激励的方法,控制思想为在塔架振动增加,需要控制干预情况下,主动减小变桨速度,以牺牲少量发电量的代价,换取塔架激励力的减小,从而达到保护风机和保证风机不停机运行的作用,总体上减小故障时间从而增加发电量。
风机叶片设计好之后,风机模型经线性化处理。可得到变桨角度相对于塔架推力的偏导数。进而可以求出各个变桨角度点中不同变桨速度下的推力变化值。
制定控制目标值,发电量不低于额定发电量的80%;塔架塔顶单元振动加速度小于0.8m/s2。
变桨限制参数确定如下:
a.确定计算变桨角度点(如10°),确定一个初始的变桨速度限制下限(如-2°/s)。变桨速度上限依据集中变桨控制算法给出,因变桨速度上限有保证风机安全作用,且不是塔架振动主导参数,故本算法不去干涉。
b.根据变桨角度限值由bladed软件根据推力偏导数和模拟风况,给出塔顶加载力。
c.加载力带入塔架模型求响应加速度。
d.确定加速度是否超标,超标则缩小变桨速度限制下限值的绝对值(如-1.8°/s),重新b、c2步,直到塔架塔顶单元振动加速度小于目标值为止。
e.应用得到的参数在bladed软件通过外控程序仿真,确认对功率影响是否在目标值之内。
一般变桨速度限制下限参数会是一个区间,如果对功率影响很小,可以进一步缩小变桨下限绝对值,重做b,c,e步找到最佳匹配参数。
在应用激励减缓变桨策略只在塔架振动有增大趋势时应用,在塔架振动恢复正常时退出,所以基本不会造成发电量的损失,但对因振动导致的风机告警和停机确有明显的避免效果。图1为相同风况下策略应用前后bladed仿真的塔架振动情况,桨距角变桨下限为-0.4 °/s。

图1 塔架振动峰峰值
由图1可知,抑制振动效果明显。经统计,10min仿真过程,策略应用前发电323kW,策略应用后发电311kW,发电量损失不到4%。
此策略在于张北风场实验进行,与相邻机组比较,一个月内,未使用激励减缓策略的机组报前后振动告警17次,振动停机2次;实验机组报前后振动告警4次,未发现振动停机现象。
4结束语
研究应用有限元思想,建立了风机塔架有限元结构动力学模型;研究了应用塔架动力学方程求解塔架模态频率及模态振型的计算过程,并应用此计算方法,以许继2兆瓦风机塔架数据为算例,计算出了相应的模态频率及振型,并分析了塔架制造安装过程中塔架基础、塔架质量及塔架刚度对其一阶模态频率的影响,即得出了基础刚度在3×1010以下时对模态频率影响巨大的结论,显示做好塔基的重要性;得出了塔架质量对模态频率的影响趋势,为塔架增加点质量提供依据;得出了塔架刚度对模态频率的巨大影响,揭示了塔架制造选材的重要性;给出了塔架模态频率的设计依据。在对塔架动力学方程相应求解研究中,研究了振动叠加法的求解过程,并找到了塔架振动控制的方法-激励减缓法;并给出了利用振动方程求解过程迭代得出相应变桨控制限值的方法。仿真及风场实验结果表明,激励减缓法在塔架振动异常时能有效减小激励,恢复塔架振动正常水平,保证风机运行平稳,进而提高总体发电量。
参考文献:
[1]陶学军,卢晓光.基于控制方法的风机塔架减振研究.机电工程,2014,31(3):325-329.
[2]王大为,陶学军,卢晓光. 基于柔性叶片模型的独立变桨减载控制. 电力系统保护与控制,2012,40(16):111-115.
[3]张涛,胡立锦,张新燕,等.风力发电机通用化建模研究.电力系统保护与控制,2013,V41(13):1-6.
[4]FreudereichK,ArgyriadisK.Windturbineloadlevelbasedonextrapolationandsimplified.WindEnergy,2008(11):589-600.
[5]BurtonT,SharpD,JenkinsN,etal.Windenergyhandbook.England:Wiley,2001.
[6]张丰豪,何榕. 基于柔性多体动力学的风力发电机固有振动频率研究.中国电机工程学报,2014,33(11):1807-1814.
[7]刘香,高镇宁,任文军,等. 基于振型分解法的风力机塔架抗震设计. 广西大学学报(自然科学版),2013,38(1):36-41.

