UAV无动力螺线下滑纵向自适应非线性制导律设计
UAV无动力螺线下滑纵向自适应非线性制导律设计
黄得刚1,章卫国1,邵山2,王志刚2,张秀林2,杨立本1
(1.西北工业大学自动化学院,陕西西安710072; 2.沈阳飞机设计研究所,辽宁沈阳110035)
摘要:针对无人机失去推力后如何跟踪一条螺线下滑路径的纵向制导问题,提出了一种纵向自适应非线性制导方法。该方法首先利用几何关系推导出纵向制导律;其次将其转化为一个二阶黏性阻尼振荡系统,并由此证明了制导律的稳定性;然后为改善制导系统的收敛时间以及抗干扰能力,设计了一种制导律的自适应方案;最后将所提出的方法用于无人机失去推力后螺线下降的纵向路径跟踪过程。仿真结果表明,与非自适应制导方法相比,无论有或无常值风扰动,所提出的方法均可提高系统的跟踪精度。
关键词:无动力;自适应;非线性制导; UAV;螺线下降;粘性阻尼振荡
近年来,美国NASA和其他国家的一些科研机构逐步开始重视飞行器迫降过程自动化的研究,并取得了一些成果,如美国密歇根州立大学[1],澳大利亚昆士兰科技大学[2-4]等,这是由于固定翼飞行器具备这种无动力滑翔能力,一旦将这种能力实现自主化,飞行器的安全性以及应用范围将得到很大提升。
当UAV失去推力后,为了使其安全到达指定降落点,设计跟踪期望滑行路径的制导方法是核心任务之一。航迹点跟踪是一种常规的路径跟踪方法,该方法在给定的路径上选取一系列航迹点,飞行器在这些航迹点上飞过,这样就可以近似跟踪一条给定的路径[5]。然而,航迹点跟踪方法仅仅是一种近似,随着跟踪曲线曲率的增加,这种近似误差会逐渐增大,另外在给定路径的情况下,航迹点不能够为飞行器的控制系统提供路径曲率的完整信息,而且当噪声和不确定性存在时,这种开环方法可能会导致飞机位置上的误差增大。向量场的方法是另外一种路径跟踪算法。向量场路径跟踪算法在期望路径周围构建一个导引飞机想期望路径靠近的向量场,该方法在鲁棒性方面是显著的,可以保证飞机渐近收敛到期望的路径,并且跟踪误差为零。但是从实际应用的角度出发,该方法的在线计算量大,不适合实时的应用[6]。Park提出了一种简单实用的制导方法,类似于导弹的比例导航制导方法,该方法简单实用,而且该方法在有动力的飞机上得到了实际飞行验证[7],虽然该方法在有动力飞机的制导中较为有效,但是针对飞机无动力滑翔这一特殊情况,该方法的效果并非十分理想,这是因为在该制导律的设计中,飞机到期望轨迹的参考点距离是固定的,这样横向制导律的输出完全由滑翔的速度来决定,这使得纵向速度的变化对横向制导会产生影响,降低横向的制导精度。Pau提出了一种自适应的制导策略[8],该制导策略在距离给定路径较远时会产生较大的侧向加速度,而距离较近时产生较小的加速度,这样加速了制导算法的收敛时间,但是该方法设计过程复杂,计算量大,对于实时性要求高的无动力滑翔状态来说并不适用,这是因为如果路径规划系统产生了安全返回的路径,如果在制导系统中产生了较大延时,会对飞机的无动力安全着陆带来不利的影响。从控制的角度讲,为了让飞机平稳返回机场,纵向需要控制滑翔速度,横向需要控制倾斜角和侧滑角来调整航向;从制导的角度讲,纵向制导律输出需要跟踪的理想滑行速度,而该速度恰是横向制导指令的输入,当滑翔速度出现扰动时,会立刻影响到横向制导的跟踪精度,从而降低了整个制导系统的跟踪精度,同时阵风对无动力无人机的影响十分显著,所以为了提高无动力滑行的制动精度,本文基于自适应的思想,提出了一种跟踪下滑螺线的纵向自适应非线性制导方法,并将该方法用于无人机无动力螺线下滑的制导过程,仿真结果表明,分别在有无常值风扰动的情况下,相比于非自适应的制导方法,本文提出的方法均提高了系统的跟踪精度。由于发动机故障和天气灾害是航空事故的主要因素[9],本文研究的前提假设为发动机失效故障,操纵面偏转正常,在此基础上设计无动力滑翔的制导律。
1 纵向非线性制导律的设计
如图1所示,当飞机向跟踪一条给定曲线路径时,需要在该路径上选取一个参考点Pref,然后向参考点做半径为R的圆弧靠近,L1为飞机当前位置到参考点之间的距离,η为飞机当前位置和参考点之间的直线与空速V的夹角,该角度用于计算需要产
生的横向加速度ascmd,即
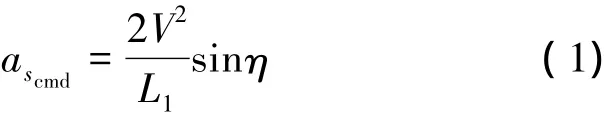

图1 制导的几何逻辑
纵向几何制导逻辑如图2所示,由于采用潜下滑角滑行,故可对η和η1做小角度假设
sinη≈η,sinη1≈η1(2)
螺线下降过程采用笛卡尔坐标系下的螺线方程

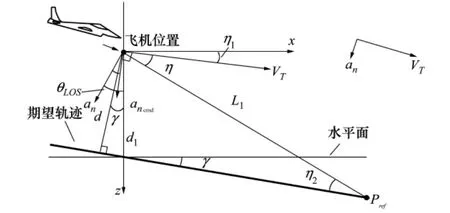
图2 纵向几何制导逻辑
式中,ω为匀速螺线下滑的偏航角速率,R为螺线轨迹半径,t为飞行时间,γ为航迹角。
则飞机当前高度和期望轨迹的高度差d1为
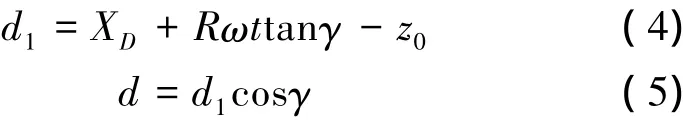
式中,XD为飞机当前高度,z0为给定轨迹的初始高度。
又知
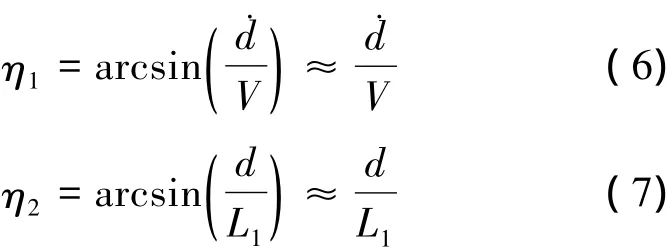
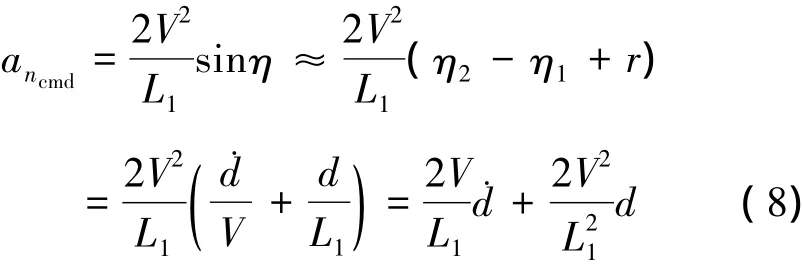
然而纵向加速度指令并不是沿d方向的加速度指令,往往需要将ancmd加速度指令进行转换,转换为沿d方向的加速度指令,此时有

由于纵向采用空速控制器,所以当得到纵向过载时,需要将纵向过载转换为所需的空速指令,则
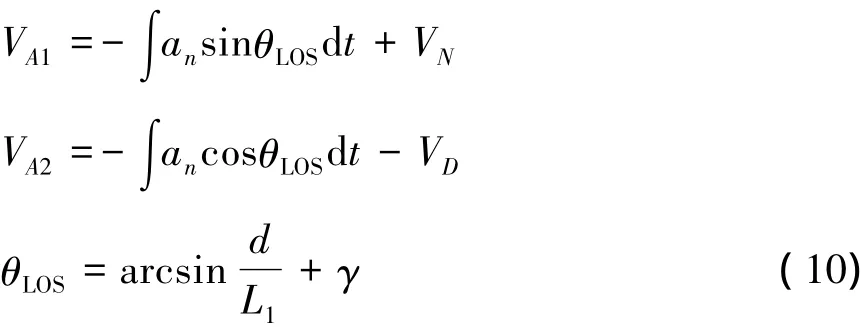
式中,VD为飞机沿z轴的速度分量,VN为沿x轴的速度分量,VA1和VA2分别为x轴和z轴的期望速度指令,可以通过飞机的输出的下降速度得到。从而总的速度指令为
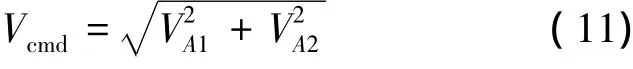
2 制导律的稳定性分析
如图3所示。
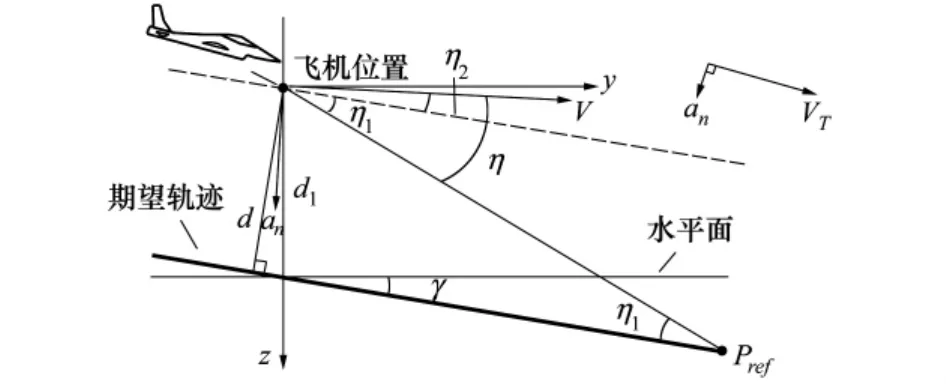
图3 下滑跟踪直线示意图
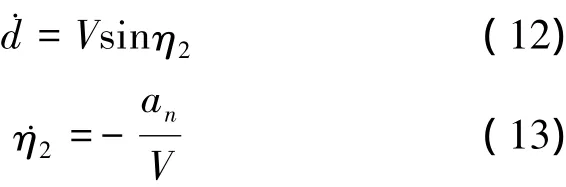
而横向加速度指令an由(1)式确定。
假设d>L1,-<η<,选取Lyapunov函数
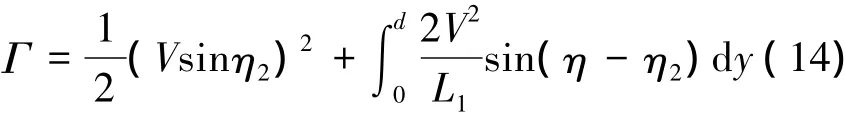
由图3可知
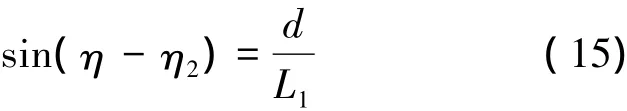
将(15)式代入(14)式可得

易知(16)式是正定函数,对时间t求导可得
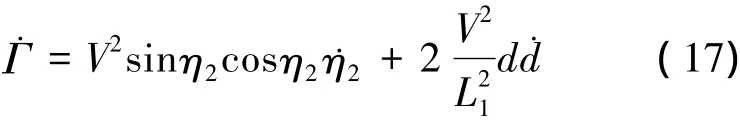
将(12)式、(13)式、(15)式代入(17)式可得
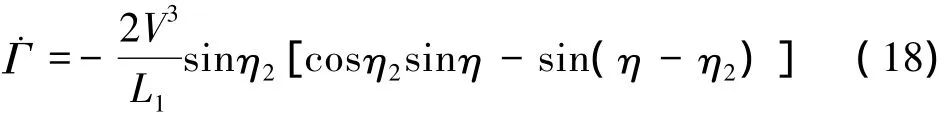
又由于
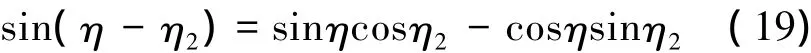
从而(18)式变为
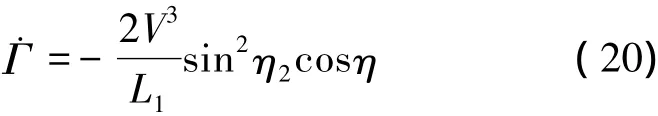
3 自适应方法
观察(8)式可以发现,该纵向制导律可以近似为一个PD控制器,其中空速V和距离L1共同决定了PD控制器的增益,然而本文纵向采用空速控制器,目的是将空速稳定在一个给定值上,这样空速V对该制导律的增益影响不大,主要的影响增益的量是距离L1的大小。
根据上述小角度假设可知,η2较小,则有

从而方程(8)式可变为
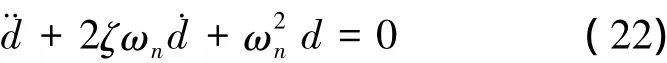
由0<ζ<1知,制导律(22)具有欠阻尼特性,由衰减系数公式σ=ζωn可知,当ζ固定时,选择合适的自然频率ωn,可以改善该制导律的衰减时间。我们希望当飞机到给定路径的距离大时,控制器产生大的纵向加速度信号,距离减小时,横向加速度信号的也随着减小,同时具备抗阵风干扰的能力,由(22)式可知,只调整参数L1就可以调整制导律的自然频率,也就可以调整纵向加速度震荡的衰减速率。为了对参数L1进行优化,本文设计了如下自适应方法。假设距离参数L1具有如下
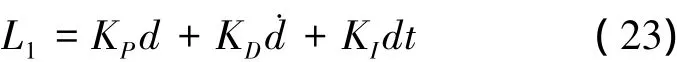
式中,t为时间间隔,KP,KD和KI为自适应调整参数,为了使得(22)式的通解
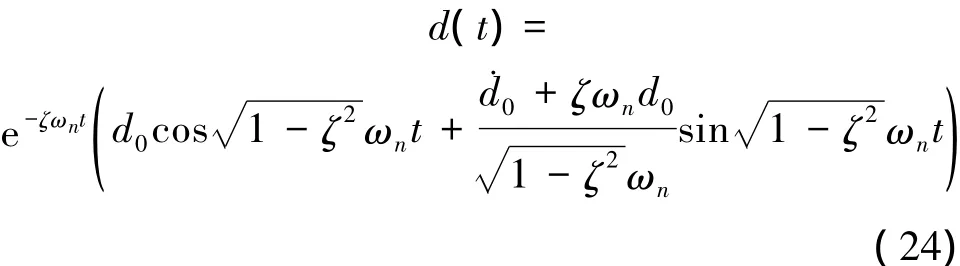
快速收敛到零,其中d0、0分别为d、的初值,设计如图4所示的自适应调整结构。
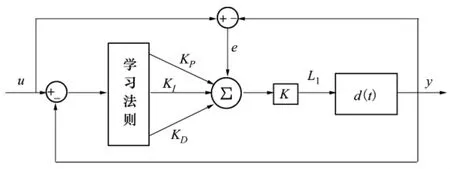
图4 自适应结构图
结构图中的学习法则采用改进的有监督Hebb学习算法,这样迭代优化算法如下[16]:
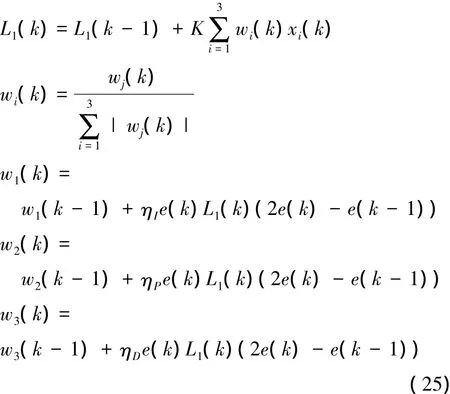
式中ηI,ηP,ηD分别为积分、比例、微分的学习速率,K为神经元的比例系数,K>0,w为神经元的连接权值,e为期望输入和实际输出之间的误差。
4 仿真结果
本文采用matlab2010a下的Simulink环境来对无人机无动力下滑过程进行仿真。根据配平结果给出期望跟踪的螺旋线轨迹,然后利用制导与控制系统验证本文提出的自适应制导律的有效性,同时采用到给定路径的平均偏移距离作为衡量该制导与控制系统的性能指标,该性能指标形式如下
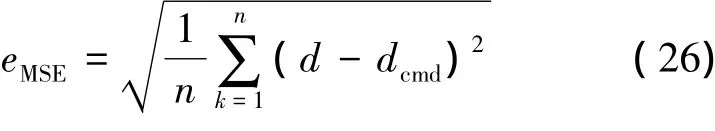
式中,d-dcmd为飞机到给定路径的偏移距离。
本文仿真时间设定为300 s,初始位置设定为x = 0,y = 2 000,z = 3 000(单位为m),初速度为31. 197 5 m/s,三维螺旋线跟踪图解如图5所示,实线是给定的期望轨迹,虚线为实际飞行的轨迹。

图5 三维制导与控制系统的跟踪螺线图
将三维跟踪图分解到纵向平面,同非自适应制导方法的跟踪效果进行对比,其中实线为给定轨迹,虚线为系统的跟踪轨迹,图6和图7为纵向非自适应跟踪示意图和相应的跟踪误差,图8和图9为自适应跟踪示意图及相应的跟踪误差。
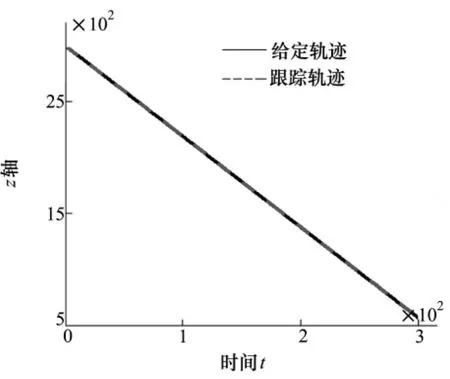
图6 纵向跟踪高度跟踪图

图7 纵向高度跟踪误差图
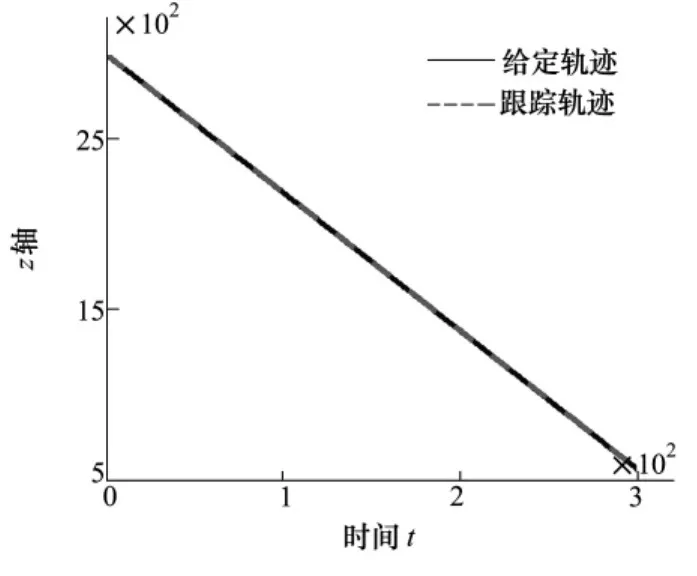
图8 纵向自适应跟踪高度跟踪图
利用给定的性能指标可以计算常规制导律跟踪的平均偏差为eMSE= 0. 979 2 m,自适应制导律跟踪的平均偏差为eMSE=0. 598 9 m。
为了模拟风速的影响,当飞机螺线下降时,在飞机上叠加一个常值风速扰动信号,加了扰动之后的纵向跟踪误差如图10和11所示。
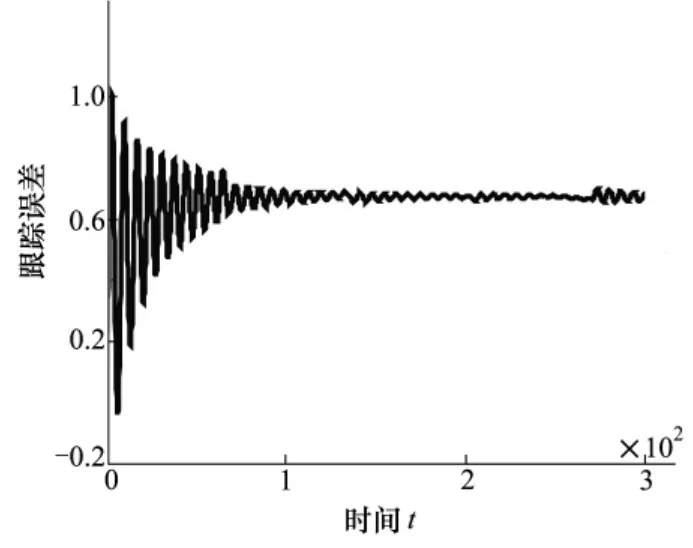
图9 纵向自适应高度跟踪误差图

图10 非自适应纵向跟踪误差
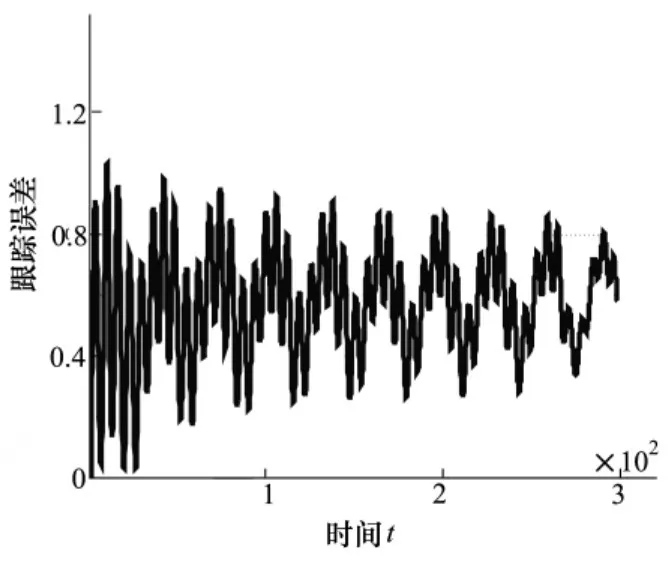
图11 自适应纵向跟踪误差
根据给定的性能指标计算得到非自适应制导律的平均跟踪偏差为eMSE= 1. 151 9 m,自适应制导律跟踪的平均偏差为eMSE=0. 623 9 m。
综上所述,与非自适应方法相比较,无论有无常值风扰动,所提出的制导方法均提高了整体系统的跟踪精度。
5 结论
在飞行过程因故障突然失去推力时,无人机只能靠滑翔进行无动力返场着陆,此时飞机的长周期变量起主要作用,这使得系统收敛到稳定状态的时间较为缓慢,为了提高制导系统的收敛速率和跟踪精度,以及使制导系统具备抵抗常值风扰动的能力,本文针对滑翔阶段的螺旋线下滑过程提出了一种纵向自适应非线性制导方法,并同非自适应制导方法进行了对比,从实验结果可知,有无常值风扰动的情况下,所提出的方法在跟踪精度上均高于非自适应制导方法,而且本文设计的自适应方法可以在线调整制导系统自然频率,避免了人工调整参数的费时过程。另外,该方法具备通用性,不但可以应用于无人机的无动力滑翔制导过程,有人飞机的迫降的制导系统也可以采用这种方法。
参考文献:
[1]Ella A.Emergency Landing Automation Aids: An Evaluation Inspired by US Airways Flight 1549[C]∥AIAA Infotech@ Aerospace Conference,Atlanta,Georgia,2010: 3381-3398
[2]Eng P,Mejias L,Liu X,Walker R.Automating Human Thought Processes for a UAV Forced Landing[J].Journal of Intelligent and Robotic Systems,2010,57(1/2/3/4) : 329-349
[3]Mejias L,Eng P C.Experimental Validation of an Unpowered Unmanned Aerial System: Application to Forced Landing Scenarios[C]∥Digital Proceedings of the 2012 International Conference on Unmanned Aircraft Systems,2012
[4]Mejias L,Eng P.Controlled Emergency Landing of an Unpowered Unmanned Aerial System[J].Journal of Intelligent&Robotic Systems,2013,70(1/2/3/4) : 421-435
[5]Dobrokhodov V.Cooperative Path Planning of Unmanned Aerial Vehicles[J].Journal of Guidance,Control,and Dynamics,2011,34(5) : 1601-1602
[6]Ratnoo A,Hayoun S Y,Granot A,Shima T.Path Following Using Trajectory Shaping Guidance[J].Journal of Guidance,Control,and Dynamics,2014,38(1) : 106-116
[7]Park S,Deyst J,How J P.Performance and Lyapunov Stability of a Nonlinear Path Following Guidance Method[J].Journal of Guidance,Control,and Dynamics,2007,30(6) : 1718-1728
[8]Pau B,Samuel L,Antonios T,Ali S.Adaptive guidance for UAV Based on Dubins Path[C]∥AIAA Guidance,Navigation,and Control (GNC) Conference,2013,American Institute of Aeronautics and Astronautics
[9]Boeing Corporation.Statistical Summary of Commercial Jet Airplane Accidents[EB/OL].(2014-04-09)[2015-04-08].http: / / www.boeing.com/news/techissues/pdf/statsum.pdf.
[10]黄得刚,章卫国,张秀林.无人机无动力滑行横向自适应非线性制导律设计[J].控制理论与应用,2014,31(11) : 1486-1491
Huang Degang,Zhang Weiguo,Zhang Xiulin.Design of the Lateral Adaptive Nonlinear Guidance Law for Unpowered Unmanned
Aerial Vehicle Gliding[J].Control Theory&Applications,2014,31(11) : 1486-1491 (in Chinese)
Design of Longitudinal Adaptive Nonlinear Guidance Law for Unpowered UAV Helix Gliding
Huang Degang1,Zhang Weiguo1,Shao Shan2,Wang Zhigang2,Zhang Xiulin2,Yang Liben1
(1.Department of Aufomatic Control,Northwestern Polytechnical University,Xi'an 710072,China 2.Shenyang Aircraft design and Research Institute,Shenyang 110035,China)
Abstract:For the longitudinal guidance problem that how to track a helix path when the UAV loses power,we present a method of the nonlinear adaptive longitudinal guidance to track a given falling spiral.Firstly,the guidance law is obtained with the geometric relationship.Secondly,the guidance law is transformed to a two-order viscous system with damping and oscillation,based on which the guidance stability is proved.Then we design an adaptive scheme for the guidance laws in order to improve the convergence time of the system and its anti-disturbance rejection capability.Finally the presented method is used to track the falling spiral when the UAV loses the thrust.The simulation results and their analysis show preliminarily that,compared with other non-adaptive method as,the proposed method improves the tracking accuracy of the system,despite being constantly subjected to wind disturbance.
Key words:unpowered; adaptive; nonlinear guidance; UAV helix gliding; viscous damped oscillations; acceleration; Lyapunov functions
作者简介:黄得刚(1986—),西北工业大学博士研究生,主要从事飞行器路径规划、制导与控制研究。
收稿日期:2014-09-28基金项目:国家自然科学基金(61374032)资助
文章编号:1000-2758(2015) 02-0309-06
文献标志码:A
中图分类号:V249.31

