对一道南通中考题的特色分析

茅雅琳

[摘 要] 南通中考数学卷在知识内容、题型、题量、难度等方面总体保持稳定，重视对知识、技能、能力和情感状况的考查，适度体现对学生解决问题能力的要求. 文中以一道南通中考题为例，分析试题特色. 该题紧扣课标要求，把握考查方向；立足教材原题，注重能力立意；拓宽思维空间，引爆精彩解法.

[关键词] 课标要求；教材原题；解法特色

原题再现

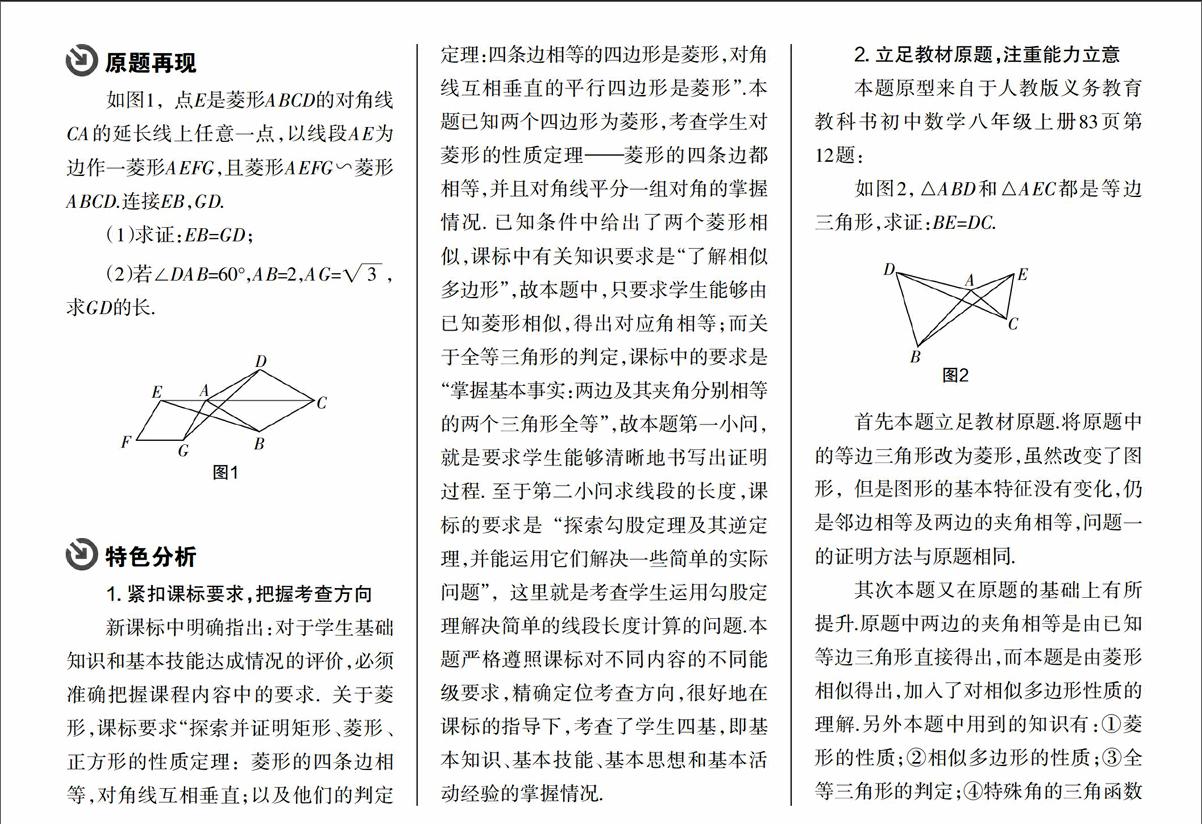
如图1，点E是菱形ABCD的对角线CA的延长线上任意一点，以线段AE为边作一菱形AEFG，且菱形AEFG∽菱形ABCD.连接EB，GD.

（1）求证：EB=GD；

（2）若∠DAB=60°，AB=2，AG=，求GD的长.

特色分析

1. 紧扣课标要求，把握考查方向

新课标中明确指出：对于学生基础知识和基本技能达成情况的评价，必须准确把握课程内容中的要求.关于菱形，课标要求“探索并证明矩形、菱形、正方形的性质定理：菱形的四条边相等，对角线互相垂直；以及他们的判定定理：四条边相等的四边形是菱形，对角线互相垂直的平行四边形是菱形”.本题已知两个四边形为菱形，考查学生对菱形的性质定理——菱形的四条边都相等，并且对角线平分一组对角的掌握情况. 已知条件中给出了两个菱形相似，课标中有关知识要求是“了解相似多边形”，故本题中，只要求学生能够由已知菱形相似，得出对应角相等；而关于全等三角形的判定，课标中的要求是“掌握基本事实：两边及其夹角分别相等的两个三角形全等”，故本题第一小问，就是要求学生能够清晰地书写出证明过程. 至于第二小问求线段的长度，课标的要求是“探索勾股定理及其逆定理，并能运用它们解决一些简单的实际问题”，这里就是考查学生运用勾股定理解决简单的线段长度计算的问题.本题严格遵照课标对不同内容的不同能级要求，精确定位考查方向，很好地在课标的指导下，考查了学生四基，即基本知识、基本技能、基本思想和基本活动经验的掌握情况.

2. 立足教材原题，注重能力立意

本题原型来自于人教版义务教育教科书初中数学八年级上册83页第12题：

如图2，△ABD和△AEC都是等边三角形，求证：BE=DC.

首先本题立足教材原题.将原题中的等边三角形改为菱形，虽然改变了图形，但是图形的基本特征没有变化，仍是邻边相等及两边的夹角相等，问题一的证明方法与原题相同.

其次本题又在原题的基础上有所提升.原题中两边的夹角相等是由已知等边三角形直接得出，而本题是由菱形相似得出，加入了对相似多边形性质的理解.另外本题中用到的知识有：①菱形的性质；②相似多边形的性质；③全等三角形的判定；④特殊角的三角函数值；⑤二次根式的运算；⑥勾股定理.这些初中数学的重要概念定理的有效整合使本题显得大气磅礴.

最后，本题的编制注重能力立意.第一小问，利用两边及其夹角证明两个三角形全等，意在考查学生的演绎推理能力；至于第二小问，通过分解图形，可以发现，其实质就是如图3的三角形中，已知两边及其夹角，求第三条边DG的长，这就需要学生具备一定的分析问题和抽象概括的能力，同时也考查了学生的计算能力.

3. 拓宽思维空间，引爆精彩解法

本题满分10分，全市均分为7.36分，难易程度适中.第一小问，与教材原题类似，学生得分率较高，这样就保证学生在获得基本分的前提下，腾出更多的时间思考第二小问，由此，在阅卷中涌现了很多精彩的解法：

解法1（如图4）：

延长CD，GA交于点H，可证得∠H=90°.

在菱形ABCD中，∠DAB=60°，

所以∠1=30°，∠EAG=∠BAD=60°.

所以∠2=30°.

所以AH=AD·cos30°=，DH=AD·sin30°=1.

在Rt△HDG中，

GD

解法特色 先利用30°角的三角函数值求出线段AH和DH的长，再利用勾股定理，求出线段GD的长.考查了对勾股定理的掌握程度，以及解直角三角形和运用勾股定理解题的能力.

解法2（如图5）：

作DH⊥AB于H，连接GH.

因为∠DAB=60°， 所以∠1=30°，

所以∠GAB=∠DHA=90°，

所以AG∥DH.

又在Rt△ADH中，

AH= AD·cos60°=1，DH= AD·sin60°=，

所以AG=DH.

所以四边形AGHD是平行四边形.

所以GD=2DO=2.

解法特色 先通过一组对边平行且相等构造平行四边形，利用勾股定理求出GD的一半，再由平行四边形对角线互相平分这一性质得GD的长.考查了对平行四边形的判定和性质的运用.

解法3（如图6）：

连接BD，

在菱形ABCD中， BD⊥AC.

又因为∠DAB=60°，

所以∠1=30°.

在Rt△ABO中，BO=1，AO=；

在Rt△EBO中，EB=.

由△ABE≌△ADG得GD=EB=

解法特色 借助第一小题证得的结论，将所求线段GB转化为求线段EB的长，再利用菱形的对角线互相垂直，由勾股定理可求得线段的长.考查了菱形的性质及勾股定理的运用.

解法4（如图7）：

如图，建立平面直角坐标系，

可求得点D的坐标为（，1），

点G的坐标为-.

由勾股定理得

DG=.

解法特色 通过建立直角坐标系，将求线段的长转化为求两点之间的距离，考查了对平面内点的坐标的理解，以及数形结合与转化思想在数学解题中的运用能力.

由于不同的学生对问题的理解程度不同，解决问题的策略不同，表现出来的解题方法不尽相同.以上四种解法中，解法1和解法4，是直接求出线段的长，而解法2和解法3，则是间接法计算.其中解法2，先求出线段的一半；而解法3，利用问题1中已得出的结论，先求线段BE的长；至于解法4，建立平面直角坐标系，借助坐标算出线段的长度，体现了很好的转化思想.以上四种解法殊途同归，最后都用勾股定理求得线段的长.

总之，本题既能以学生为本，注重考查学生的四基，给学生以较为广阔的解题切入口，又能有效引领教师的教学，注重培养学生的思维能力.中考试题的编制是命题教师认真研读课标，钻研教材的结晶，认真分析试题，可以帮助一线教师明确命题方向，把握教学动态，更好地为学生服务.

本文成稿过程中，参考了南通市教研室袁亚良老师所作的讲座《新课程下中考数学试卷的命制技术》，在此表示感谢.endprint