精馏塔广义预测控制器设计

（沈阳化工研究院设计工程公司，沈阳 110021）

精馏过程一般是个被控对象系统模型参数随时间变化的过程，对于蒸馏过程可以采用传统的PID控制，但是效果未必是理想的，近年来发展的广义预测控制对于系统模型参数变化有很好的自适应调节能力[1-2]，但是此种算法的计算量比较大，而近年来随着半导体工业片上系统的发展，使得可以采用片上系统来实现某些先进控制算法控制化工生产过程，实现过程不复杂，控制效果较传统的PID控制要好，并能显著提高产品收益，尤其对于精细化工来说，能显著提高经济效益。对于点数多，系统比较大的系统采用成品DCS解决方案比较合适，一般DCS厂家有相应的先进控制软件包通过组态来实现先进控制算法是比较好的方案，或者采用OPC方式购买独立的软件包实现[3]；但是对于系统较小或者生产规模比较小的生产车间，采用DCS来解决，从成本来说就不是很经济，而且要有相应的维护人员，对于一般的小厂家这个未必现实，所以，这种先进控制算法在点数少或者小车间实现的不多。如果能采用带有先进控制算法的一体化数字控制器，比如：数显表或者带有控制功能的无纸记录仪，在小车间或者点数少的控制系统实现先进控制算法，从经济和现实上是比较合理的，同时能提高相应企业的经济效益。本文针对点数少，生产规模小的车间设计一个采用先进控制算法的控制器，控制器硬件上采用片上系统ST32F407微控制器，控制器上运行嵌入式操作系统，先进控制算法的编程实现基于操作系统的调度算法。

1 控制器设计

1.1 硬件设计

控制器芯片采用STM32F407VET6，此种SoC芯片带有浮点运算单元，对于复杂控制算法和矩阵运算非常有优势，而且实时性也能保证，造价也比DSP要低。控制器显示部分由2排4位连体数码管组成，通过2个74HC595串联来驱动数码管，上面一排显示实际测量值，下面一排显示设定值；4个按键分别是参数设定键、增加键、减少键、回车键；还有2个发光二级管，红色的是电源指示灯，绿色的是控制输出，还有2个报警灯，可根据需要设定为高限报警和低限报警。控制器的输入输出主要包括信号的变换及放大，输入输出较为复杂一些，下面介绍。

1.1.1 万能输入

输入采用万能输入，一般蒸馏过程的控制量主要是温度、压力等，对于温度信号，测量温度仪表的输出信号有热电阻、热电偶、0～10 V、或者 4～20 mA的标准电流信号等几种输入，压力一般是4～20 mA、0～10 V信号。由于工业上一般采用三线制热电阻输入，就需要的输入端子数来说最多的是热电阻信号，所以万能输入的端子数是3个。如何在3个端子上可以实现热电阻、热电偶、0～10 V、4～20 mA信号的输入，是万能输入电路需要解决的问题。具体实现的方案本质上就是通过多路转换来实现，具体实现有电子的转换开关如CD4052，ADG801/802，机械式的拨码开关，放大倍数的切换通过CD4052，ADG801/802来实现；如果输入的是热电偶信号，温度补偿可通过三极管的集电极和基极短接作为二极管来实现的，用三极管主要是考虑这种补偿效果比二级管效果好。具体实现的电路可以有好几种，根据实际可能碰到的输入信号形式来具体选择。

本产品根据实际情况出发，采用4～20 mA和三线制热电阻输入，由于要在4～20 mA和热电阻信号之间进行切换，模拟开关要选择导通电流大的，导通电阻小的，这种情况要选择ADG801/802，这款模拟开关与CD4052比，导通电流大并且导通电阻小足以满足需求，AG801与ADG802的区别是输入逻辑信号是相反的。经过电路变换后的电压直接接入STM32F407的15引脚ADC123_IN10。具体实现如图1所示。

图1 控制器输入Fig.1 Input of controllor

图中 K1、K2、K3、K4、K5、K6、K7、K12选 ADG801，K8、K9、K10、K11选ADG802， 用一个引脚控制这些开关，即把所有这些开关都连接到一个逻辑输出引脚上，当为高电平时代表热电阻输入，低电平时代表4～20 mA输入。一个引脚控制所有开关也实现了互锁，这是由于ADG801/ADG802输入逻辑相反，2个输入电路只有1个有效。

1.1.2 控制器输出

控制器的输出采用4～20 mA输出，由于微处理器的D/A转换输出时电压信号，这就需要一个电压到电流转换的电路，电路的电压信号取自STM32F407的29引脚DAC_OUT1，具体实现如图2所示。

图2 控制器输出Fig.2 Output of controllor

1.2 软件设计

厂家已经把这款芯片的UCOSIII移植到这款SoC芯片上了，只要参考对应的程序，把没有的外设加到操作系统上就可以了，具体过程略。

UCOSIII这种操作系统有基于时间片轮转的调度策略，对于熟悉PLC或者DCS的人来说基于这种调度编程比较容易上手，基于时间片就是每隔1个固定时间就执行一次时间片内的任务，整个程序由不同时间片的任务组成。根据实际经验，GPC算法可以在5 min的时间片内，即GPC采样周期设为5 min，PID在1 min左右的时间片，及PID采样周期设为1 min，显示单位任务在30 s时间片任务内，采样任务安排在30 s的任务内。系统启动流程如图3所示。

图3 软件系统的启动流程Fig.3 Start of software system

2 控制算法

由于蒸馏过程随着产品和组分的不同，相应的回流比也是不一样的，同时系统的动态模型也是不一样的，并且控制系统有时滞，对于要求较高的蒸馏单元操作常规的串级控制，往往不能满足需求。为了适应这种模型参数的不确定，蒸馏过程采用广义预测控制加PID控制，组成GPC-PID串级控制。GPC算法执行的时间间隔大于PID算法。此算法不但能利用当前及过去时刻的系统输出而且能利用将来时刻的预测输出来进行控制，对于系统的时滞有较好的抑制，控制精度和系统的抗干扰性都有较好的提高，算法要先辨识出系统模型，再根据变化的数学参数设计控制器，由于模型实时变化，控制器也是根据这个变化在线实时做相应改变。同时底层也采用了PID算法，这种算法适应能力强，鲁棒性好，GPC-PID串级控制算法，充分发挥先进控制算法和常规的算法的优势。蒸馏过程的被控量是塔底温度，副对象是流量，如图4所示。

图4 蒸馏塔广义预测串级控制Fig.4 Cascade control system of distillation tower

2.1 广义预测算法[4]

系统模型采用CARIMA模型[5]（受控自回归积分滑动平均模型），即：

各项系数 ai（1≤i≤na），bi（0≤i≤nb），ci（1≤i≤nc）为过程需要辨识的参数。基于此加热过程不是很复杂取 na=2，即：A（z-1）＝1+a1z-1+a2z-2；除 b3，b4外，其余涉及 b 的系数都为 0，即：B（z-1）=bcz-3+b4z-4，系统时滞为 3 个采用周期即为 3 min，d=3；C（z-1）=1。算法流程如图5所示。

图5 广义预测算法流程Fig.5 Algorithm of general predictive control

具体广义预测算法如下：

已知：na、nb及 d。

步骤 1设置初值和 P（0），输入初始数据，并设置控制参数 N、N1、N2、Nu，以及控制加权矩阵、输出柔化系数 α、遗忘因子 λ 等；其中估计参数列向量的初值取初值 0，P（0）＝106I，N1=3，N2=N=4；Nu=4，控制加权矩阵取单位阵，阶次为4，输出柔化系数α=0.7，遗忘因子λ=1；

步骤2采样当前实际输出y（k）和参考规矩输出 yr（k+j）；

参考输出取为

式中，ω为温度设定值，这个需要根据工艺条件给定。

步骤3利用遗忘因子递推最小二乘法[6]：

即在线实时估计被控对象参数θ^，A^、B^；

步骤4求解Diophanine方程：

解出多项式 Ej、Gj和 Fj；

步骤 5构造向量 Yr、ΔU（k-j）、Y（k）及矩阵G、F1、F2：

为过去的控制向量；

步骤 6利用式

u（k）＝u（k-1）+Δu（k）

计算出 u（k）；

步骤7返回Step2（k→k+1），继续循环。

2.2 PID算法

蒸馏过程一般用调节阀控制流量，采用位置式PID，但是对于控制器计算来说采用增量式，最后再转换成位置式PID，具体算法如下：

步骤1计算控制增量Δuk：

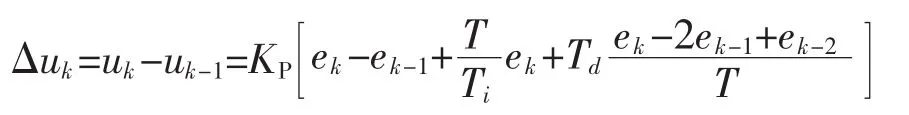
步骤 2计算 uk：uk=uk-1+Δuk

式中：uk、uk-1、Δuk分别为当前时刻和前一时刻的控制输出及当前时刻的控制器增量；ek、ek-1、ek-2分别为前一时刻，和前两时刻的设定值与实际测量值之差。

3 结语

通过设计广义预测控制器，在UCOSIII上实现GPC-PID串级控制算法，能够实时辨识蒸馏过程的动态系统模型，从而根据新的模型动态调整控制器算法。在控制蒸馏过程的实际应用中，由于广义预测控制器在设计控制器时不但考虑了系统过去和当前的状态信息而且考虑了系统未来输出，所以能更好地抑制系统由于反应过程产生的模型参数改变带来的扰动，而且对于模型参数较大范围的改变也能够得到很好的控制效果，而常规PID控制对于较大范围的参数扰动可能会失效，或者产生不稳定现象，此种控制较常规的PID控制更能适应参数的改变，控制效果更好。在实际应用中，由于这种控制器算法本身能够自动辨识系统的参数，其参数调整能自动完成，不需要人工干预，适应性更强，这种控制器成本低、效果好、可维护性比较高、易于实现，对于小系统或者小的实验室系统，及对于控制要求又比较高的情况非常适用，具有很好的推广价值。

[1]Filatov N M，Unbehauen H.Survey of adaptive dual control methods[J].IEEE Proc.Control Theory Appl，2000，147（1）：118-128.

[2]Witenmark B.Stochastic adaptive control methods：A survey[J].International Journal of Control，1975，21（21）：705-730.

[3]OPC foundation.OPC Data Access Custom Interface Specification 3.0[M]，2003

[4]庞中华，崔红.系统辨识与自适应控制MATLAB仿真[M].北京：北京航空航天大学出版社，2009.

[5]韩曾晋.自适应控制[M].北京：清华大学出版社，1995.

[6]Astrom KJ，Wttenmark B.Adaptive Control[M].北京：科学出 版社，2003.