基于小波神经网络的多电机偏差耦合控制研究

黄文军，郗欣甫，孙以泽

（东华大学 机械工程学院，上海 201620）

随着工业4.0、智能工厂和智能工业等概念的提出，智能制造已成为全球制造业发展的新趋势，智能设备和生产手段在未来必将广泛替代传统的生产方式[1]。作为复杂多轴体的智能装备，多轴协同控制技术将会得到进一步的广泛应用。协同控制精度的高低直接影响着自动控制系统的稳定性，也将影响产品生产线的质量。

小波神经网络是基于小波分析理论所构造的一种具有多分辨率的神经网络，充分利用了神经网络对任意复杂函数的逼近能力和计算能力以及小波变换的时频局部特性和变焦特性，可以自适应地调整小波基的形状实现小波变换，使得整个网络相比传统神经网络学习能力更强，收敛速度更快[2]。本文在偏差耦合结构的基础上融入了小波神经网络，提出了基于小波神经网络的偏差耦合多伺服电机协同控制策略，利用小波神经网络强大的学习能力和快速收敛性，以在保证系统良好动态性能的同时，使得系统具有优良的同步特性。

1 偏差耦合控制结构优化设计

偏差耦合协同控制是利用各个拖动子系统之间的惯量关系在速度反馈环节中增添比较电机的速度信号，根据每个子系统的工作状态动态分配补偿速度，从而达到同步的目的。在系统工作时，速度补偿器将控制轴的转速与其他轴的转速比较，然后由补偿算法对偏差进行处理，输出该轴的转速补偿信号wc。由于偏差耦合方案考虑了所有运动轴的偏差值，使各轴的误差都得到约束，能根据自身及其他轴的运动情况进行同步调节，因此具有较好的同步性能。偏差耦合控制结构如图1所示。

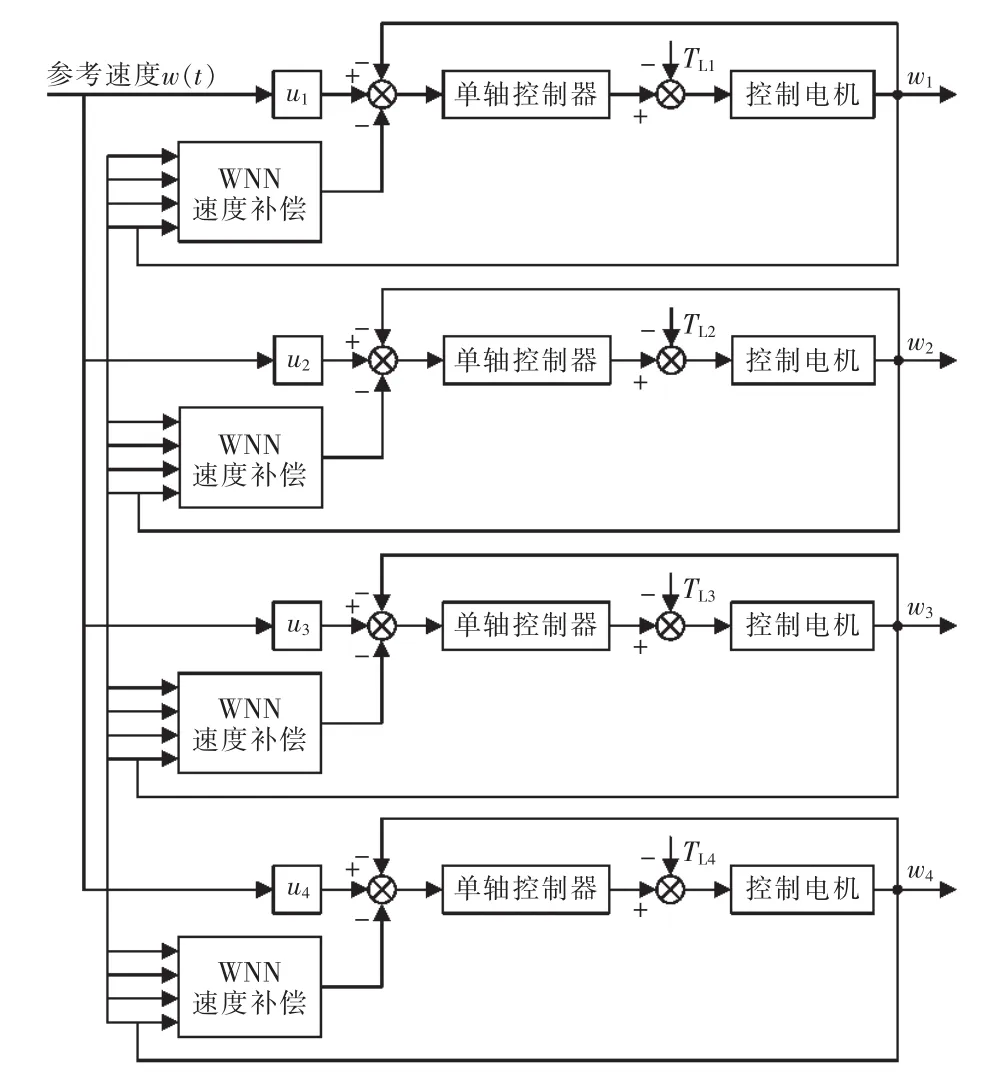
图1 基于小波神经网络补偿器的偏差耦合多伺服电机协同控制结构Fig.1 Relative coupling control structure of multi-servomotor synchronization based on wavelet neural network compensative controller

对于一个包含4台电机的同步控制系统，假定系统中各电机之间速度的关系为w1/u1=w2/u2=w3/u3=w4/u4，将系统的同步误差定义为

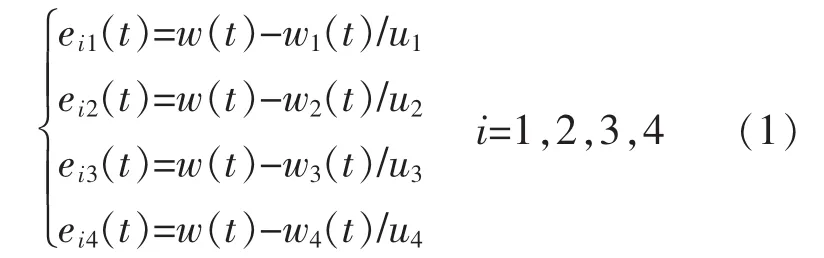
式中：w（t）为系统参考速度；eii（t）为第 i台电机与系统其它子电机的同步误差。很明显，要满足系统的同步要求，应使第i台电机与其他电机的同步误差稳定收敛，即满足式（2）：

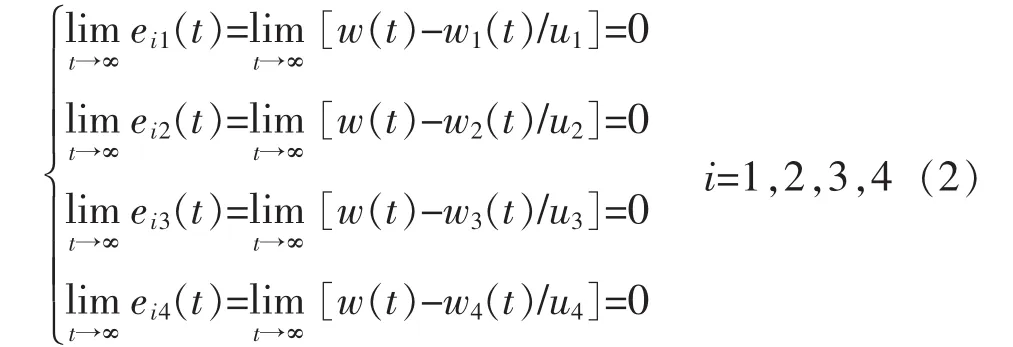
由图1可知，偏差耦合控制中最重要的部分是速度补偿器，由它给每台电机提供速度补偿信号，传统的速度补偿器如图2所示。

图2 固定增益补偿器结构Fig.2 Structure of the fixed-gain compensative controller

图 2 为固定增益速度补偿器，其中，K12，K13，K14为速度耦合补偿增益，其作用类似于比例控制，其计算公式为[3]

式中：Ja为控制电机的转动惯量；Jb为与控制电机速度作差的电机转动惯量。由图2可知，第1台电机的速度补偿值为

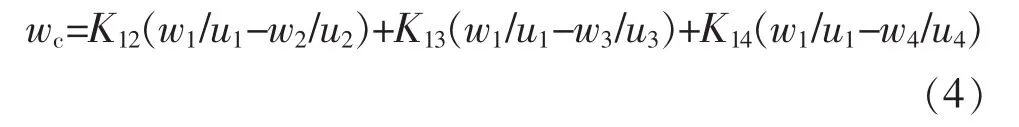
固定增益速度补偿器补偿形式单一，各电机子系统的特性参数不同，导致各子系统的速度波动大，且消除波动时间长，造成了多电机间速度的不同步，出现同步误差。对于每一个子系统而言，其他任意子系统的波动都是一种干扰，而这种干扰是可测且经常变化的，故可以通过算法对干扰进行学习预测，对干扰进行补偿，实时消除干扰对子系统的不良影响，很好地提高系统的控制品质。本文采用小波神经网络控制器代替固定增益，快速补偿偏差，实现干扰的快速消除，其结构如图3所示。

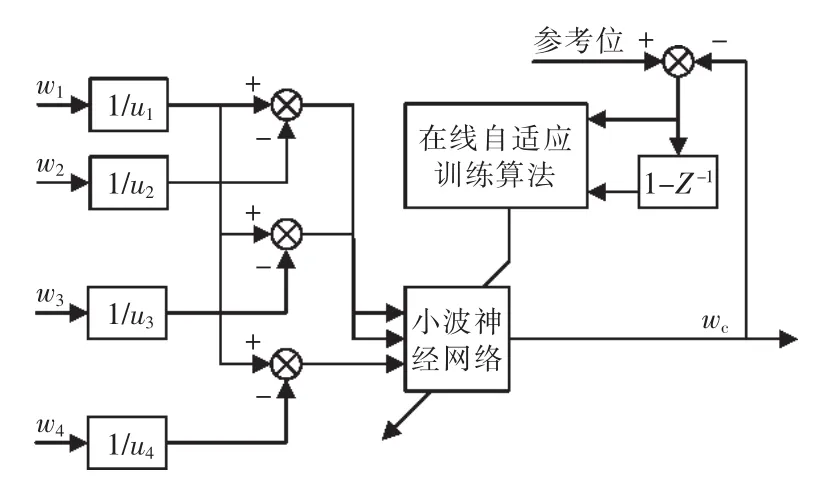
图3 小波神经网络补偿器结构Fig.3 Structure Of the wavelet neural network compensative controller

图3所示的速度补偿器即为图1中的WNN速度补偿，以第1台电机为例，将第1台电机与系统其他子电机的同步误差作为小波神经网络的输入，网络的输出为速度补偿值，可以自适应地调节输出值的大小，使系统具有良好的同步性能。引入参考位，使参考位与网络实际输出值作差后形成参考误差信息，作为自回归小波神经网络在线训练的输入信号，从而使整体网络的输出可以满足同步误差的要求。小波神经网络的各项参数由自适应算法调整好自动修正，使得系统具有优良的自学习能力和自适应性。

2 小波神经网络补偿器

2.1 小波神经网络结构

在多伺服电机协同控制系统中，永磁同步电机作为控制对象，具有非线性以及强耦合等特性，一般的控制方法难以达到满意的控制效果。针对神经网络收敛速度慢以及模糊PID控制不具有自适应性等缺点，利用小波神经网络的学习能力和收敛能力，本文将小波神经网络融入速度补偿器，设计了小波神经网络速度补偿器，如图4所示。

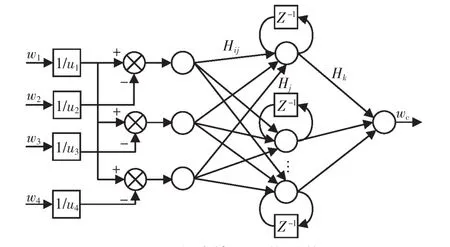
图4 小波神经网络结构Fig.4 Structure of neural network

小波神经网络具有1个输入层、1个隐层和1个输出层。隐层神经元的作用函数选择一阶微分的高斯小波函数，表示为

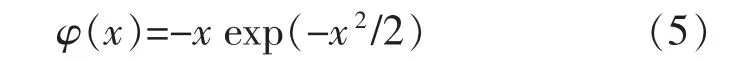
对于输入层各节点，网络的输入输出可表示为

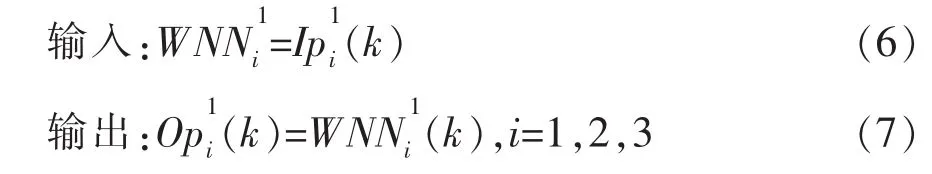
式中，变量的上标和下标数字分别代表网络的层数和k时刻的输出数。

对于隐层各节点，加入了单元的自反馈：

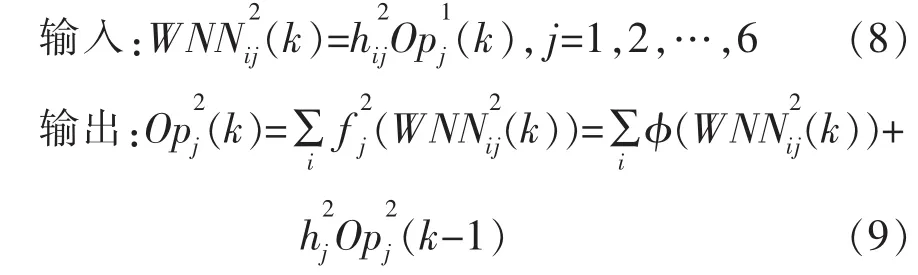
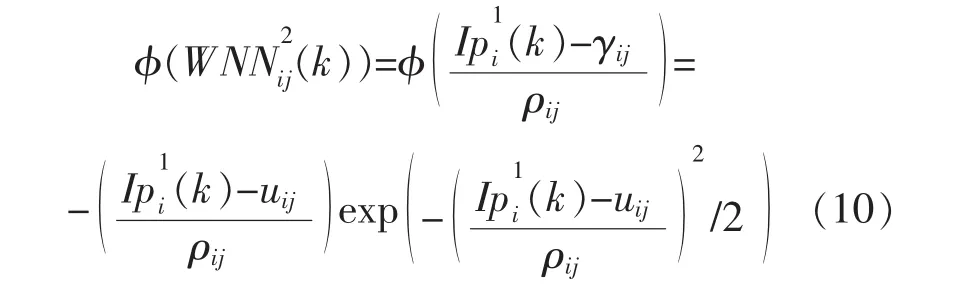
式中，mij和rij是平移和伸缩参数，将母波函数平移和伸缩变换成各式小波函数，可对输入信号进行处理提取有用的信息。

对于输出层节点：

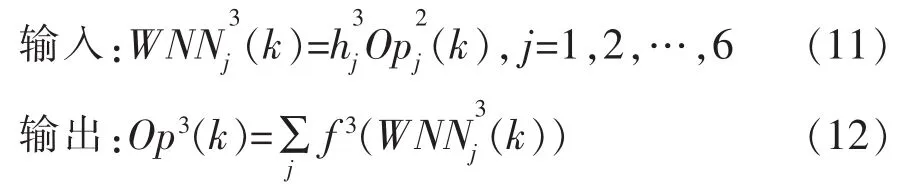
2.2 在线训练算法

小波神经网络的参数需要经过在线训练不断地调整从而适应控制系统的不确定性，因此选择有监督的反向传播算法训练和更新网络参数。定义能量函数为

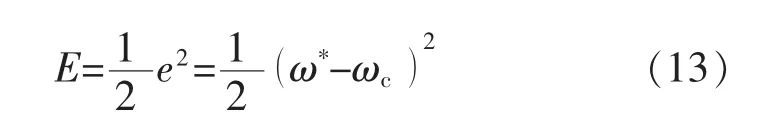
式中，ω*为参考位，因此，输出层传播的误差项为

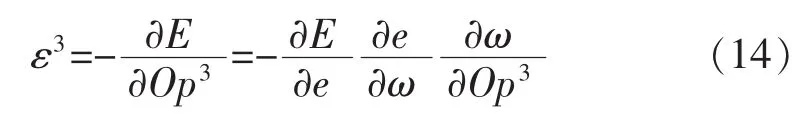
因此，隐层到输出层连接权重调整因子为

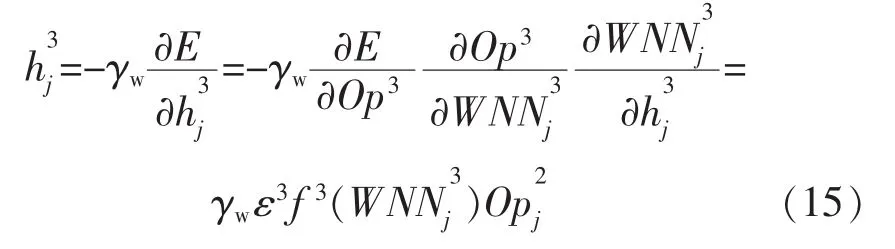
式中，gw是隐层到输出层的连接权重参数的学习率。

隐层的递归项权重调整因子：

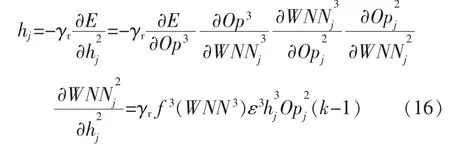
式中，gr为隐层自回归权重参数的学习率。

小波函数平移参数和伸缩参数的调整因子可以分别计算如下：

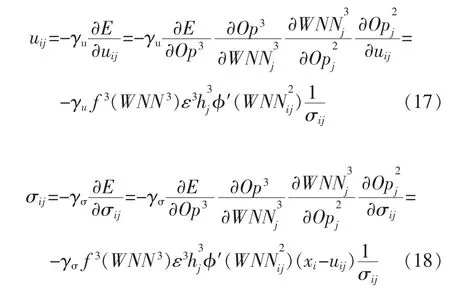
式中，gm和gs是小波函数参数的学习率。网络各参数可通过调整因子实时更新。

由于运动控制系统本身的非线性及电机参数变化引起的不确定性，使式中的∂w/∂Op3难以求得，为解决此问题同时提高网络参数的在线学习速率，因此，采用以下形式作为被传播的误差项：

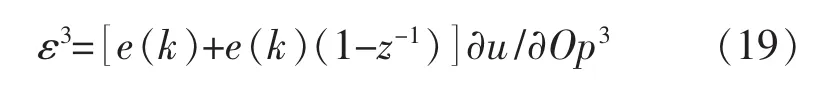
3 仿真实验与结果分析

3.1 仿真参数设置

为了验证上述同步控制方案速度补偿的有效性，以4台永磁同步电机为例，基于Matlab/Simulink平台进行了仿真实验。4台电机在id=0矢量控制策略下的各主要参数设置如表1所示。

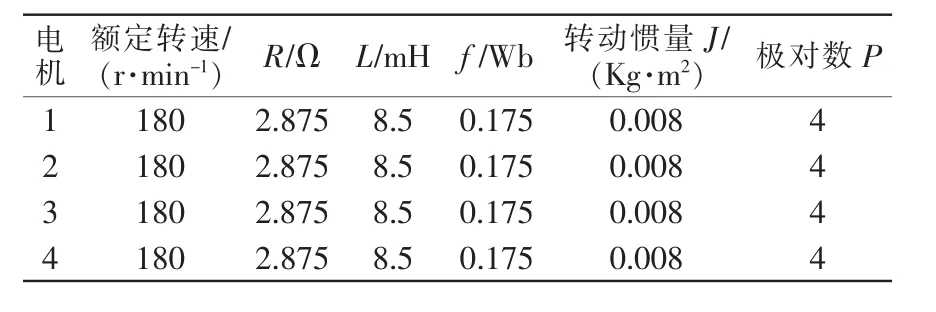
表1 4台电机的参数设置Tab.1 Parameters settings of four motors

小波神经网络输入层连接隐层以及隐层连接输出层加权系数的初始值选取均值为0，方差σ2=1，标准差σ=1的正态分布的随机数为

3.2 小波神经网络偏差耦合结构仿真实验

设定系统的参考速度 w（t）=180 r/min，4 台电机在相同工况下启动，仿真时间为0.2 s。在t=0.08 s时刻，分别给各个电机施加扰动，扰动值分别为2 N·m、4 N·m、8 N·m 和 12 N·m。4台电机的速度响应曲线和同步误差曲线如图5、图6所示。

3.3 仿真实验结果分析

由图5可知，固定增益补偿器和WNN补偿器均能实现多伺服电机的协同控制，而与固定增益补偿器相比，WNN补偿控制下4台电机能够更快地到达稳定状态。当4台电机受到扰动影响时，WNN补偿控制能使系统重新快速准确地跟踪目标，速度波动小、调节时间短。

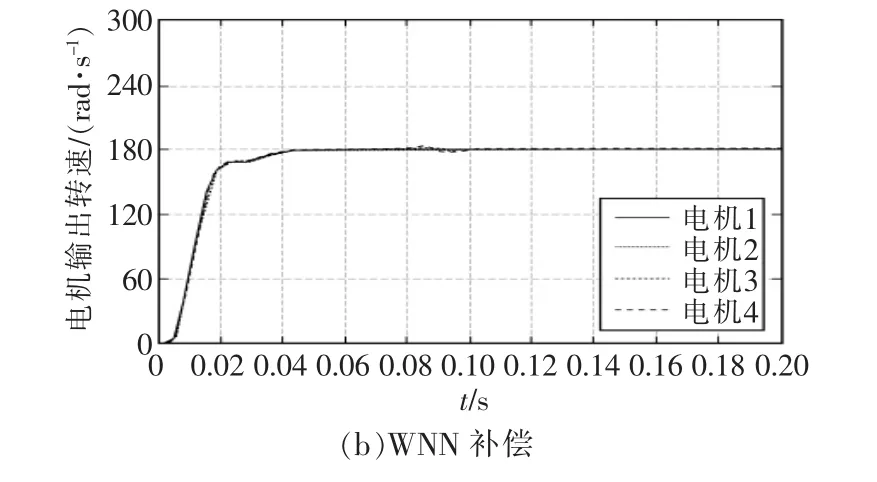
图5 偏差耦合结构速度响应曲线Fig.5 Speeds of four PMSM under the wavelet neural network relative coupling control

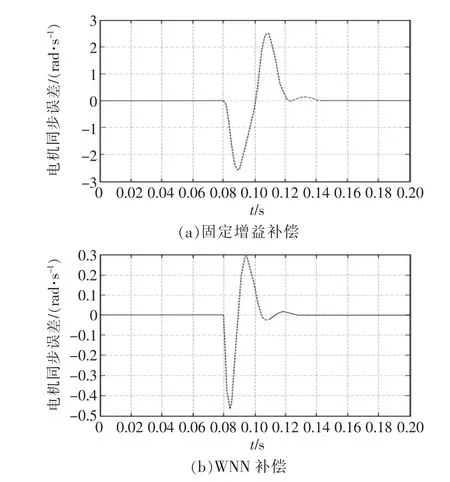
图6 偏差耦合结构电机同步误差曲线Fig.6 Synchronization deviations of four PMSM under the wavelet neural network relative coupling control

由图6可知，WNN补偿器在对多伺服电机系统的同步误差控制方面性能更加优越。与固定增益补偿器相比，在系统发生扰动时，WNN补偿控制下的多伺服电机系统同步误差更小，消除系统误差速度更快，体现了较好的同步性能。

4 结语

本文将小波神经网络运用到了偏差耦合协同控制的速度补偿器中。根据多轴系统中各运动轴间的同步误差，利用小波神经网络对任意形状函数的逼近能力和学习能力，WNN速度补偿器对因扰动产生的偏差进行补偿，实现系统的自适应性。仿真实验结果表明，采用文中所设计的WNN速度补偿器，比固定增益补偿器能够更好地实现同步控制，提升同步品质，也为多伺服电机的协同控制提供了参考借鉴。

[1]罗文.德国工业4.0战略对我国推进工业转型升级的启示（节选）[J].PLC&FA，2014（9）：36-39.

[2]苗新刚，汪苏，韩凌攀，等.基于偏差耦合的多电机单神经元同步控制[J].微电机，2011，44（2）：44-47.

[3]季明逸，游有鹏.基于偏差耦合法的同步控制策略研究与实践[J].中国制造业信息化，2012，41（21）：58-61.

[4]彭晓燕，刘威，张强.基于改进型偏差耦合结构的多电机同步控制[J].湖南大学学报：自然科学版，2013，40（11）：77-83.

[5]曹春平，王波，胥小勇，等.基于神经网络多电机偏差耦合同步控制结构[J].控制工程，2013，5（3）：415-418.

[6]刘达.造波机系统运动控制及其网络化技术研究[D].大连：大连理工大学，2013.

[7]王小川，史峰，郁磊.MATLAB神经网络43个案例分析[M].北京：北京航空航天大学出版社，2014.

[8]高飞.MATLAB智能算法超级学习手册[M].北京：人民邮电出版社，2014.

[9]刘云平.基于人群搜索算法的PID控制器参数优化[J].计算机仿真，2014，31（9）：347-350.

[10]程斯一，纪文刚，王志俊.基于模糊PID的多伺服电机交叉耦合同步控制[J].北京石油化工学院学报，2014，22（4）：54-57.

[11]胡寿松.自动控制原理[M].5版.北京：科学出版社，2007：76-121.

[12]Sun D，Tong M C.A synchronization approach for the minimization of contouring errors of CNC machine tools[C]//IEEE Transactions on Automation Science and Engineering，2009，6 （4）：720-729.

[13]Yao B，Hu C X，Wang Q F.An orthogonal global task coordinate frame for contouring control of biaxial systems[C]//IEEE/ASME Transactions on Mechatronics，2012，17（4）：622-634.

[14]Yang J Z，Li Z X.A novel contour error estimation for position loop-based cross-coupled control[C]//IEEE/ASME Transactions on Mechatronics，2011，16（4）：643-655.

[15]Hu C X，Yao B，Wang Q F.Coordinated adaptive robust contouringcontrollerdesign foran industrialbiaxialprecision gantry[C]//IEEE/ASME Transactions on Mechatronics，2010，15（5）：728-735.