基于岭估计和L曲线的损伤识别技术研究

第一作者 郭惠勇 男，博士，副教授，1971年生

基于岭估计和L曲线的损伤识别技术研究

郭惠勇1, 罗乐2, 盛懋1, 李正良1

(1. 重庆大学 土木工程学院, 重庆400045; 2. 成都城电电力工程设计有限公司，成都610041)

摘要：为了解决结构损伤方程求解的可靠性问题，提出了基于岭估计和L曲线的损伤方程求解方法。首先描述了基于模态应变能灵敏度的结构损伤方程，然后考虑测量噪声等因素易造成病态的损伤方程问题，提出了采用岭估计求解结构的损伤方程，并利用L曲线确定最优的岭参数，最后建立了损伤估计值的修正方法。数值仿真结果表明，基于修正的岭估计和L曲线方法可以较为精确地识别出损伤的位置和程度，而且其定量识别结果明显好于基本的岭估计和L曲线方法以及一般的截断奇异值分解法。

关键词：损伤识别；损伤方程；岭估计；L曲线；位移模态

基金项目：国家自然科学基金(51468058);教育部留学回国人员科研启动基金(20121707)

收稿日期：2014-02-08修改稿收到日期：2014-04-03

中图分类号:TB123文献标志码： A

Structural damage identification method based on ridge estimation and L-curve

GUOHui-yong1,2,LUOLe2,SHENGMao1,LIZheng-liang1(1. School of Civil Engineering, Chongqing University, Chongqing 400045, China;2. Chengdu Chengdian Electric Power Engineering Design Co., Let., Chengdu 610041, China)

Abstract:In order to solve the reliability problem of structural damage equation, a damage detection method based on ridge estimation and L-curve was presented. Firstly, a structural damage equation based on modal strain energy sensitivity was described. Then, considering measurement noise easily making the damage equation be ill, the ridge estimation was utilized to solve the damage equation and L-curve is utilized to identify optimal ridge parameters. Finally, an improved ridge estimation method was proposed to enhance the identification precision. Simulation results demonstrated that the proposed ridge estimation and L-curve methods can detect structural damage locations and level with good accuracy, their quantitative detection results are obviously better than those of the basic ridge estimation and L-curve methods and the truncated singular value decomposition method.

Key words: damage identification; damage equation; ridge estimation; L-curve; displacement modal shape

工程结构在投入使用后，由于环境的作用，常会产生各种损伤。结构的严重损伤会引起建筑物的倒塌或者失效，从而造成巨大的经济和人员生命的损失。因此，对结构损伤的识别研究一直是国际上的研究热点[1-3]。利用损伤前后动力特性的改变，建立相应的损伤方程，从而求解出损伤系数是较为有效的方法[4-5]。但是，在工程实际中，测试数据不可避免的会受到测量噪声、环境因素等的干扰，常会使损伤方程产生病态问题，从而给直接求解带来困难，造成损伤的解极不稳定，与真实值相差较远。这样，损伤方程组的求解和精度成为问题的症结。采用截断奇异值分解算法(TSVD)能够减少方程的参数空间，使损伤方程组变的数值稳定[6-7]。但是，该方法需要人为的选择截断误差或者截断水平，不同的截断误差或截断水平会产生不同的识别结果，故选择恰当的截断误差或者截断水平决定了方程求解的精度。而结构的改变，甚至同一结构单元划分不同，都会影响截断误差或者截断水平的选取。岭估计(RE)法[8]可以较好的处理病态问题，而L曲线方法[9]可以较好地处理优化参数的选取问题，故本文拟采用岭估计和L曲线法相结合，来解决损伤方程的病态问题以及优化参数的选取问题。

1基于模态应变能灵敏度的损伤方程

基于模态应变能的损伤识别方法是较为有效的一种方法[10]，可以根据模态应变能的灵敏度建立相应的损伤方程。

第j个单元和第r阶模态的模态应变能

(1)

式中:Erj是模态应变能；Φr为第r阶质量归一化位移模态；Kj为第j个单元的刚度矩阵。则第j个单元和第r阶模态的模态应变能对任意设计参数p的敏感性为[6]

(2)

式中:λr是第r阶特征值； K和M是整体刚度矩阵和质量矩阵；p为设计参数。

当结构损伤时，其第j个单元损伤后的刚度矩阵

Kjd=Kj-cjKj

(3)

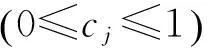
SΔC=ΔR

(4)

式中：S是系数矩阵；ΔR是残余向量；ΔC是损伤系数向量。其组成具体如下：

(5)

(6)

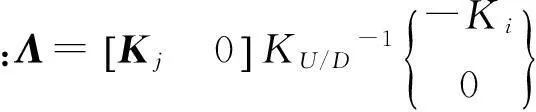
通过求解该方程可以同时识别结构的损伤位置和程度。但是，由于结构损伤常常出现在结构的局部某些位置或单元，而大部分结构单元未发生损伤，因此，在系数矩阵中常会出现几乎线性相关的列，特别是模态参数在测试时会出现噪声的干扰，故方程组的求解和精度往往成为问题的关键症结。采用截断奇异值分解法可以较为有效的处理该问题，但是，由于在现实中，损伤的位置和程度是未知的，截断奇异值分解法选择不同的截断误差或者截断水平，所得计算结果往往差别很大，从而对损伤识别结果造成较大的干扰[7]。故本文采取岭估计和L曲线法相结合，来求解损伤方程，以获取更具有可靠性的计算结果。

2岭估计和L曲线法及其改进

2.1损伤的岭估计

可以采用岭估计法求解损伤方程，以避免因测量噪声等引起的损伤方程病态问题。岭估计方法是一种在均方误差意义下优于最小二乘估计的有偏估计方法，是从Tikhonov正则化原理推导出来，该方法可以克服矩阵方程的病态性。根据Tikhonov正则化原理，对应于损伤方程岭估计的估计准则为：

(7)

(8)

式中：I为单位阵。αI项的参与，可以有效的抑制方程的病态性，从而可以得到可靠的损伤估计值。岭估计的核心是如何确定岭参数，这里选择采用L曲线法来选取恰当的岭参数。

2.2L曲线法

令

(9)

两边取对数，可得

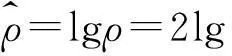
(10)

(11)

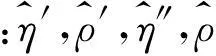
2.3估计值的修正

由于岭估计是有偏估计，而L曲线法求解的也是近似最优解，故损伤的估计值需要修正。由岭估计的估计准则方程式(7)可知，该准则是用来确定损伤系数的2-范数项最小，这样，该岭估计的解会造成近似线性的偏差，故采用简单的线性修正方式来提高识别精度。另外，损伤系数值应大于0，当损伤系数估计值小于0时，则认为是无损伤，而该项本身是由于岭估计的有偏估计造成的，故可根据所有无损单元的估计值平均偏移量来确定线性修正的幅值。这样，就可以对可能损伤单元的损伤系数估计值进行修正，修正公式如下

(12)

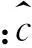
3数值算例

考虑如图1所示的一个Euler-Bernoulli简支梁。梁总长为6 m，划分为20个单元，假设未损伤结构的几何参数和物理参数如下：梁的横截面积A为0.005 m2，惯性矩I=1.67 m4，弹性模量E=32 GPa，密度ρ=2 500kg/m3，基准参数为0.25。假设有三种损伤情况，第一种情况，在单元3和12发生损伤，刚度分别降低15%和20%；第二种情况，在单元2、10、14发生损伤，刚度分别降低25%，15%和20%；第三种情况，在单元5、11、19发生损伤，刚度分别降低20%，20%和30%。分别采用截断奇异值分解 (TSVD)法和岭估计(RE)法求解损伤方程。由于低阶模态比高阶模态更能反映结构的损伤，其抗噪能力更强，而且更易被测量和获取[11]。因此，本文仅采用第1阶位移模态进行结构的损伤识别研究。岭参数的确定主要是通过对式(11)求最大值κmax，κmax所对应的点就是L曲线的所求的点。这样就定位了L曲线上曲率最大的点，这个点所对应的α值就是所求的岭参数。

图1Euler-Bernoulli梁
Fig.1 Euler-Bernoulli beam

3.1例1

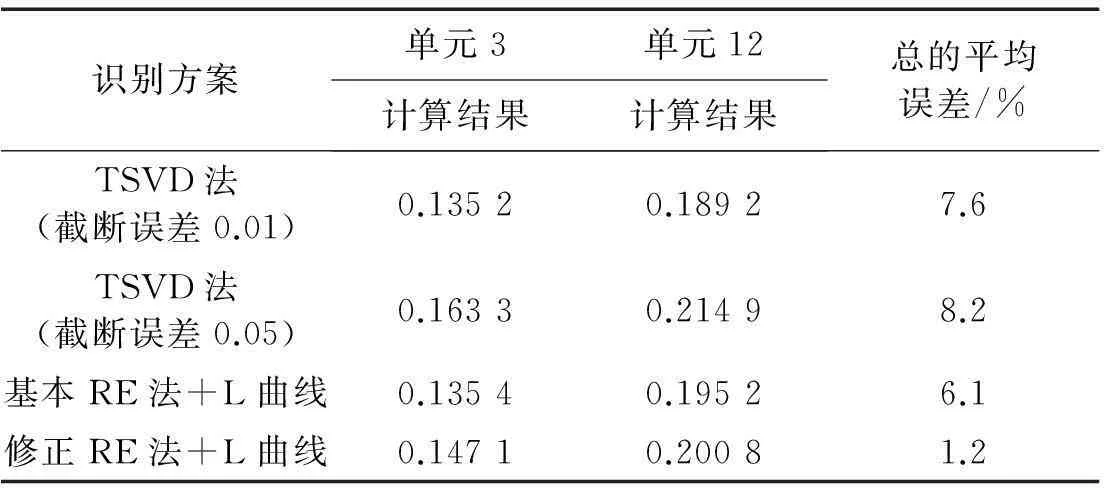
当单元3和单元12发生损伤时，其损伤系数的计算结果如图2所示。采用了四种方案，即截断误差0.01的TSVD法、截断误差0.05的TSVD法、基本RE和L曲线法，修正RE和L曲线法。其中L曲线法求得的岭参数为25.616 3。从图2中可以发现，截断误差0.01的TSVD法的损伤定位结果不理想，易对单元1和单元20产生误判，其余三种方法定位识别较好，而从定量角度分析，可以较为明显地发现修正RE和L曲线法的定量识别结果最好。将单元3和单元12的损伤系数单独提取分析，结果如表1所示。从表1可以观察到，修正RE和L曲线法的平均误差最小，识别结果最好。

图2　单元3、单元12损伤时四种损伤识别方案的识别结果 Fig.2 Identification results of four damage methods when multiple damages occur in the 3rd and 12th elements

识别方案单元3单元12计算结果计算结果总的平均误差/%TSVD法(截断误差0.01)0.13520.18927.6TSVD法(截断误差0.05)0.16330.21498.2基本RE法+L曲线0.13540.19526.1修正RE法+L曲线0.14710.20081.2

图3　单元3、单元12损伤时四种损伤识别方案的 识别结果(考虑3%的测量噪声) Fig.3 Identification results of four damage methods when multiple damages occur in the 3rd and 12th elements(considering 3% noise)

当考虑位移模态有3%的测量噪声干扰时，则四种损伤识别方案的一次计算结果如图3所示。首先从损伤定位角度分析，截断误差0.01的TSVD法已经丧失了损伤定位功能，截断误差0.05的TSVD法则具有一定的损伤定位效果，但是易对单元2和单元19产生误判，而两种RE和L曲线法的损伤定位效果较好。然后从损伤定量角度分析，从图3可知，本建议的修正RE和L曲线法相对较好。故修正RE和L曲线法不仅具有较好的定位能力，具有一定的定量分析能力。由于测量噪声具有一定的随机性，则每次考虑随机噪声的计算结果都会产生一些小的变化，故未列出定量结果的平均误差表。

3.2例2

当单元2、单元10和单元14发生损伤时，其损伤系数的计算结果如图4所示。L曲线法求得的岭参数为469.226 6。从图4中可以发现，截断误差0.01的TSVD法的损伤定位结果不理想，易对单元1、单元19、单元20产生误判，其余三种方法的定位识别结果较好，再从定量角度分析，可以较为明显地发现修正RE和L曲线法的定量识别结果最好。将单元2、单元10和单元14的损伤系数单独提取分析结果见表2。从表2可知，修正RE和L曲线法的平均误差最小，识别结果最好。

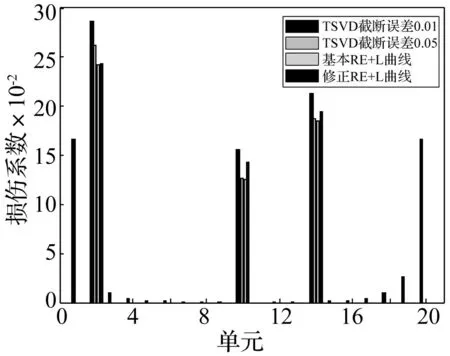
图4　单元2、单元10和单元14损伤时 四种损伤识别方案的识别结果 Fig.4 Identification results of four damage methods when multiple damages occur in the 2nd, 10th and 14th elements

识别方案单元2单元10单元14计算结果计算结果计算结果总的平均误差/%TSVD法(截断误差0.01)0.28610.15590.21348.4TSVD法(截断误差0.05)0.26290.12700.18659.3基本RE法+L曲线0.24260.12530.18499.0修正RE法+L曲线0.24360.14260.19393.5

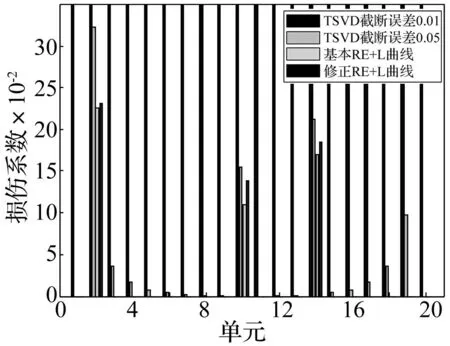
图5　单元2、单元10和单元14损伤时四种损伤识别 方案的识别结果(考虑3%的测量噪声) Fig.5 Identification results of four damage methods when multiple damages occur in the 2nd, 10th and 14th elements(considering 3% noise)

当考虑位移模态有3%的测量噪声干扰时，计算结果如图5所示。首先从损伤定位角度分析，截断误差0.01的TSVD法已经丧失了损伤定位功能，截断误差0.05的TSVD法则具有一定的损伤定位效果，但是易对单元3、单元18和单元19产生误判，而两种RE和L曲线法的损伤定位效果较好。然后从损伤定量角度分析，从图3可知，本建议的修正RE和L曲线法相对较好。由于测量噪声具有一定的随机性，故未列出定量结果的平均误差表。

3.3例3

当单元5、单元11和单元19发生损伤时，其损伤系数的计算结果如图6所示。L曲线法求得的岭参数为500.58。从图6中依然可以发现，截断误差0.01的TSVD法的损伤定位结果仍不理想，易对单元1、2和20产生误判，其余三种方法的定位识别结果较好，再从定量角度分析，可以较为明显地发现修正RE和L曲线法的定量识别结果最好。将单元5、单元11和单元19的损伤系数单独提取分析结果见表3。从表3可知，本建议的修正RE和L曲线法的平均误差最小，识别结果最好。

图6　单元5、单元11和单元19损伤时 四种损伤识别方案的识别结果 Fig.6 Identification results of four damage methods when multiple damages occur in the 5th, 11th and 19th elements

当考虑位移模态有3%的测量噪声干扰时，计算结果见图7。首先从损伤定位角度分析，截断误差0.01的TSVD法已经基本丧失了损伤定位功能，截断误差0.05的TSVD法则具有一定的损伤定位效果，但是易对单元2、3和18产生误判，而基本和修正的RE和L曲线法的损伤定位效果较好。然后从损伤定量角度分析，从图7可知，本建议的修正RE和L曲线法相对较好。由于测量噪声具有一定的随机性，故未列出定量结果的平均误差表。

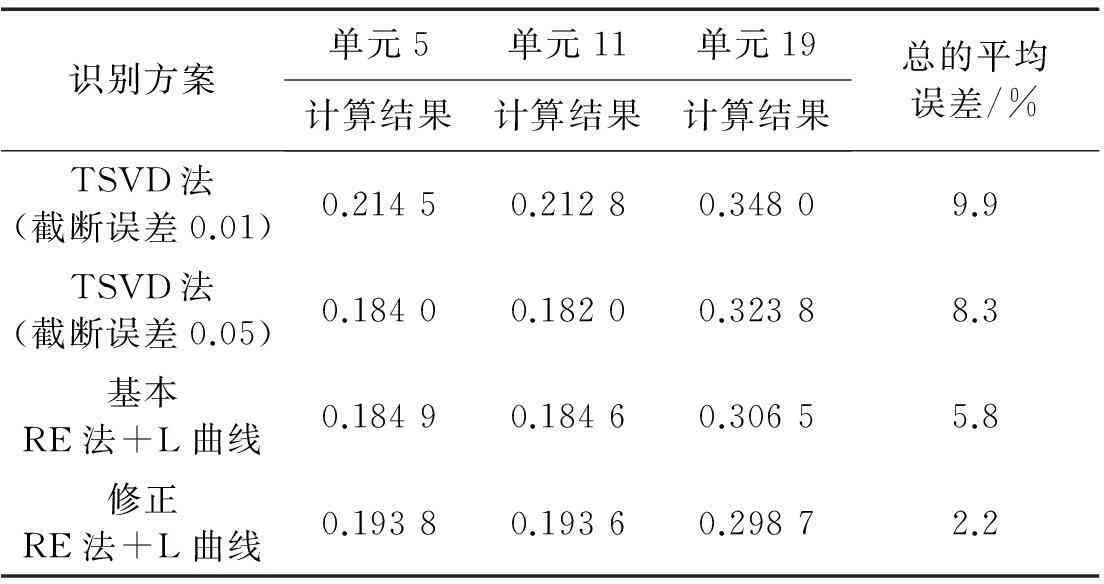
表3　例3的损伤定量识别结果

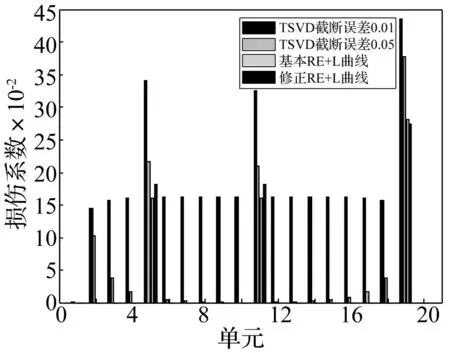
图7　单元5、单元11和单元19损伤时四种损伤识别 方案的识别结果(考虑3%的测量噪声) Fig.7 Identification results of four damage methods when multiple damages occur in the 5th, 11th and 19th elements(considering 3% noise)

从以上三个例子可以观察到，当仅采用第一阶位移模态进行损伤识别时，截断误差为0.01时，TSVD法的识别效果较差，截断误差为0.05时，TSVD法的识别效果相对较好，故TSVD法的关键是选取恰当的截断误差值。由于结构损伤是未知的，故截断误差的选择也应存在一个优化问题。当采用基本岭估计和L曲线法，其定位和定量结果相对更好，这是因为L曲线可以选择近似最优的岭参数，从而解决了参数优化问题。修正岭估计和L曲线法的识别效果最好，这是由于该方法采用了未损单元的有偏估计均值对损伤系数估计值进行了修正和改进。

4结论

提出了基于L曲线和岭估计的方法来求解损伤方程。该方法首先建立基于模态应变能的损伤方程，然后利用岭估计和L曲线法相结合来求解该方程。岭估计可以较好的处理测量噪声等引起的方程病态问题，L曲线法可以选择近似最优的岭参数，使岭估计计算结果更为可靠。最后利用未损单元的有偏估计均值对岭估计方法进行了修正和改进。数值分析结果表明，基本岭估计和L曲线法可以较可靠地求解出损伤方程，并较好地识别出结构的损伤，而修正的岭估计和L曲线法可以更可靠地进行进行损伤的定性和定量识别，该方法优于基本岭估计和L曲线法和未经过优化的截断奇异值分解法。

参 考 文 献

[1] Salawu O S. Detection of structural damage through changes in frequencies: a review[J]. Engineering Structures, 1997, 19(9): 718-723.

[2] Guo H Y, Li Z L. Structural damage identification based on Bayesian theory and improved immune genetic algorithm[J]. Expert Systems with Applications, 2012，39: 6426-6434.

[3] Seyedpoor S M. A two stage method for structural damage detection using a modal strain energy based index and particle swarm optimization[J]. International Journal of Non-Linear Mechanics, 2012, 47: 1-8.

[4] Shi Z Y, Law S S, Zhang L M. Structural damage localization from modal strain energy change[J].Journal of Sound and Vibration, 1998, 218(5): 825-844.

[5] 郭惠勇，李正良. 基于测量位移和频率的结构损伤二次识别方法[J].振动与冲击，2007，26(4): 94-96.

GUO Hui-yong, LI Zheng-liang. Two-stage structural damage identification method based on measured displacements and frequencies[J]. Journal of Vibration and Shock, 2007，26(4): 94-96.

[6] 颜王吉. 单元模态应变能灵敏度及其在结构损伤识别中的应用[D]. 长沙：中南大学,2008：38-45

[7] 张立涛，李兆霞，费庆国. 基于加速度时域信息的结构损伤识别方法研究[J].振动与冲击，2007，26(9): 138-141.

ZHANG Li-tao, LI Zhao-xia, FEI Qing-guo. Study on structural damage identification using acceleration data in time domain[J]. Journal of Vibration and Shock, 2007，26(9): 138-141.

[8] Hu Hong-chang. Ridge estimation of a semi-parametric regression mode[J]. Journal of Computational and Applied Mathematics, 2005, 176(1): 215-222.

[9] Hansen P C. Analysis of discrete ill-posed problems by means of the L-curve[J]. SIAM Review, 1992, 34(4): 561-580.

[10] 冯坤，杨永春，郑轶. 基于轴向模态应变能比法的三维桁架结构损伤定位方法[J].振动与冲击，2013，32(12): 169-173.

FENG Kun, YANG Yong-chun, ZHENG Yi. Damage detection method of a three-dimensional truss structure based on axial modal strain energy ratio[J]. Journal of Vibration and Shock, 2013，32(12): 169-173.

[11] Guan H, Karbhari V M. Improved damage detection method based on element modal strain index using sparse measurement[J]. Journal of Sound and Vibration, 2008, 309(3-5): 465-494.