Biot 理论与修正的 Biot 理论比较及讨论

第一作者 刘志军 男，博士生，1988年生

Biot理论与修正的Biot理论比较及讨论

刘志军1,2，夏唐代1,2，黄睿1,2，陈炜昀3

(1. 浙江大学 软弱土与环境土工教育部重点实验室，杭州310058；2.浙江大学 滨海和城市岩土工程研究中心，杭州310058； 3. 南京工业大学 交通学院，南京210009)

摘要：对Biot理论和修正的Biot理论中的波动方程进行了详细推导，注明了每个参数的量纲和准确含义，并基于修正的Biot理论导出了三种不同形式的波动方程；对两种理论进行比较，得到了Biot弹性系数表达式，并分析了两者的应力及其对应关系；最后，着重对易被混淆的孔隙流体压力符号的正方向和含义，以及基本方程中部分参数的定义式进行了讨论，有助于更好地理解、应用Biot理论和修正的Biot理论。

关键词：Biot理论；修正的Biot理论；弹性系数；应力；孔隙流体压力；参数

基金项目：国家自然科学基金(U1234204,51378463)

收稿日期：2013-06-26修改稿收到日期：2014-01-28

中图分类号:TU435文献标志码： A

Comparison and discussion for Biot theory and modified Biot one

LIUZhi-jun1,2,XIATang-dai1,2,HUANGRui1,2,CHENWei-yun3(1. MOE Key Laboratory of Soft Soils and Geoenvironmental Engineering, Zhejiang University, Hangzhou 310058, China;2. Research Center of Costal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China;3. College of Transportation Science & Engineering, Nanjing University of Technology, Nanjing 210009, China)

Abstract:The wave equations of Biot theory and modified Biot one were derived, and the dimension and correct definition of each parameter in the equations were clearly indicated. Based on the modified Biot theory, three different forms of wave equations were derived as well. Then, by comparing those two theories, the expressions of Biot elastic coefficients were obtained, and the stresses of the two theories and their correspondences were analyzed. Finally, particularly, the positive direction and meaning of pore-fluid pressure sign and the definitions of part parameters in the fundamental equations were discussed to be helpful for understanding and using the two theories.

Key words: biot theory; modified biot theory; elastic coefficients; stress; pore-fluid pressure; parameters

20世纪50年代，Biot[1-2]首先建立了流体饱和多孔介质传播理论(简称“Biot理论”)，其基本方程已得到广泛应用，为双相多孔介质的土动力学分析奠定了基础。Biot理论是基于热力学原理而推导出的半唯象(semi-phenomenological)理论，其中，A、R、Q 等系数太复杂且含义抽象，给实际求解带来了困难。后来的学者对其进行了一些简化和修正，提出了可以考虑固体颗粒和流体压缩性、且忽略质量耦合系数的双相孔隙介质理论(“修正的Biot理论”)，其基本方程的建立是基于弹性动力学和渗流理论，易于理解，也在一定程度上证实了Biot理论的正确性。

基于Biot理论或修正的Biot理论，国内外很多学者从不同的角度对多孔介质中的土动力学问题进行了研究。但不同文献中所应用的基本方程表达式各异，部分参数的定义式有些混乱，尤其是孔隙流体压力的正方向和内涵，及其与平均孔隙流体压力的差异容易被忽略和混淆，让人产生误解。

修正的Biot理论是基于Biot理论而提出来的，也正因为如此，往往忽略了这两个既存在联系而基本方程表达式又不同的理论之间的关系，目前尚没有相关的比较研究。本讨论主要为：① 分别对这两种理论进行详细的推导，并基于修正的Biot理论推导出不同形式的波动方程；② 比较两种理论，得到两者之间的应力关系及Biot理论中弹性系数的表达式；③ 对孔隙流体压力和其他参数进行讨论。

1Biot理论与修正的Biot理论

1.1Biot理论

Biot基于一系列假设条件，通过热力学原理建立了流体饱和多孔介质的线性本构关系，并给出了系统动能和介质耗散函数的表达式，运用拉格朗日方程，最后建立了考虑惯性项和粘性项相互耦合的系统动力方程。其基本方程如下(除特别注明之外，相同符号代表相同的参量)：

固体骨架和孔隙流体的线性本构方程(应力应变关系)分别为：

(1)

s=Qe+Rε， s=-npf

(2)

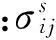
分别以单位体积饱和多孔介质中的固体和孔隙流体作为研究对象，固体和流体的运动方程为：

(3)

(4)

式中：b为Biot自定义的一个与达西渗透系数有关的介质耗散参数，b=n2η/κ=n2ρfg/k[4]；g为重力加速度(m/s2)；η为流体黏滞系数(Pa·s)；κ为固体骨架动力渗透系数(m2)；k为固体骨架固有渗透系数(m/s)；ρ11、ρ22、ρ12分别为固体、流体质量系数和固—液质量耦合系数(kg/m3)，其中，(1-n)ρs=ρ11+ρ12，nρf=ρ12+ρ22；ρs、ρf分别为固体和流体真密度(kg/m3)。

将式(1)、式(2)代入式(3)、式(4)，可得到位移矢量形式的波动方程：

N2u+grad[(A+N)e+Qε]=

(5)

grad[Qe+Rε]=

(6)

1.2修正的Biot理论

由于Biot理论中的A、R、Q、ρ12等系数太复杂且含义抽象，为此，后来的学者基于Biot理论导出了修正的Biot理论。虽然两种理论的基本方程表达式有所不同，但实质上是相通的。不同的是，修正的Biot理论中忽略了取值不易确定的质量耦合系数，即假设ρ12=0。修正的Biot理论中，位移矢量不同，其基本方程表达式也有所不同，有以下三种常用的形式：

(1) u-w形式

学者杨峻基于修正的Biot理论研究了饱和土中三种体波的弥散与衰减特性[5]，考虑了土颗粒和流体的压缩性，其基本方程如下：

以固体和流体组成的系统单元整体作为研究对象，其运动方程为：

(7)

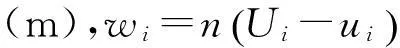
以孔隙流体自身作为研究对象，流体运动方程为(假设孔隙流体为理想的可压缩流体，其流动遵从Darcy定律)：

(8)

渗流连续方程：

(9)

式中：

(10)

式中：α、M为表征土颗粒和流体压缩性的Biot系数；Ks、Kb、Kf分别为固体颗粒、固体骨架和流体的体变模量(Pa)。

柯西问题中初始条件满足[6]：

(11)

因此，式(9)两边同时对时间t求积分，可以得到孔隙流体的本构方程(与Santos[7]中的式(1)是一致的)：

-pf=Mwi,i+αMui,i

(12)

考虑土颗粒本身由于孔隙流体压力作用所引起的压缩性，基于有效应力的应力应变关系为[8]：

σij=λξkkδij+2μξij-αpfδij

(13)

式中：λ、μ为弹性骨架的Lame常数(Pa)，后者又称剪切模量。

联立以上各式，可得到u-w位移矢量形式的波动方程：

μ2u+(λ+μ+α2M)(·u)+

αM(

(14)

αM(·u)+M(

(15)

(2) u-U形式

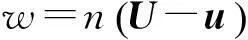
系统单元运动方程，即式(7)可化为：

(16)

孔隙流体运动方程，即式(8)可化为：

(17)

孔隙流体的本构方程，即式(9)可化为：

-pf=(α-n)Me+nMε

(18)

基于有效应力的应力应变关系，即式(13)可化为：

σij=[λ+α(α-n)M]eδij+αnMεδij+2μξij

(19)

联立式(16)～式(19)可得u-U位移矢量形式的波动方程，也即式(14)～式(15)可化为：

μ2u+[λ+μ+α(α-n)M](·U)+

nαM(

(20)

(α-n)M(·U)+nM(·U)=

(21)

(3) u-U-pf形式

将式(18)代入式(20)、式(21)，可得到u-U-pf形式的波动方程：

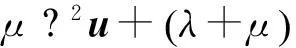
(22)

(23)

以上三种形式与黄茂松[8]基于混合物理论推导得到的结果是一致的。在研究中，当需侧重流体与固体之间的相对运动或研究对象与之相关时，可采用u-w形式的波动方程，且其式子较为简洁，得到了广泛应用；u-U形式的波动方程则更突出了双相介质的作用机理，易于理解，且可直接得到流体的绝对位移；u-U-pf形式的波动方程应用较少。

2比较

2.1Biot弹性系数

Biot和Willis[9]通过外套试验(jacketed test)和非外套试验(unjacketed test)给出了各向同性Biot波动方程中弹性系数与纯固体骨架体变模量、颗粒体变模量和流体体变模量之间的关系。Claude Depollier[10]分析了均匀和非均匀材料的Biot弹性系数表达式，李亮等[11]给出了忽略固体颗粒的压缩性时Biot弹性系数的表达式。通过对比Biot理论和修正的Biot理论，也可得出A、R、Q等弹性系数与流体饱和多孔介质各体变模量之间的关系。

由于修正的Biot理论中没有考虑质量耦合系数，因此，在对上述两种不同表达形式的波动理论进行对比时，均忽略惯性耦合项，即ρ12=0，此时有：

ρ11=(1-n)ρs，ρ22=nρf

(24)

式(21)两边同乘以n，得：

n(α-n)Me+n2M

(25)

结合式(24)，注意到b=n2η/κ，对比式(6)与式(25)，得：

Q=n(α-n)M，R=n2M

(26)

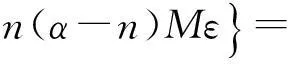
(27)

对比式(5)与式(27)，得：

N=μ，A=λ+(α-n)2M，

Q=n(α-n)M

(28)

对比式(2)与式(18)，注意到s=-npf，得

Q=n(α-n)M，R=n2M

(29)

综合式(26)、式(28)、式(29)，有

(30)

修正的Biot理论是基于Biot理论并经简化、修正后得到的。上述对比中，采用由果索因的反演分析法，得到了Biot弹性系数与多孔介质体变模量之间的关系式，同时也分析了两种理论中各基本方程的对应关系，在一定程度上验证了Biot理论的正确性，使半唯象(semi-phenomenological)的Biot理论更具体，有助于加深对其的理解。

2.2两种理论中的应力

Biot理论中，当忽略质量耦合项并假设流-固两相之间不存在相对位移，即ρ12=0、ui=Ui，则式(3)和式(4)化为：

(31)

(32)

Biot理论中，总应力σij应为(忽略质量耦合项)

修正的Biot理论中，式(19)中的σij为总应力，比较式(33)与式(19)，有：

A+Q=λ+α(α-n)M，Q+R=αnM

(34)

式(34)与前面得到的结果式(30)是一致，这也验证了上述分析的正确性。

值得注意的是，也有不少文献(如Santos、Degrande[15],徐平[16])中直接以σij表示平均固相应力或修正广义有效应力，在阅读或引用时需加以区分。

3讨论

3.1孔隙水压力

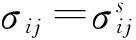
王立忠等[17-18]曾对修正的Biot理论中的孔隙流体压力进行了简要的相互讨论，下面通过一个流体运动方程对孔隙流体压力的符号定义和内涵进行详细讨论与分析。

陈龙珠等[19-22]对饱和土中体波和表面波的传播特性做了大量研究，其中，关于孔隙水的运动方程为：

(35)

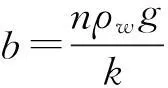
(36)

对比式(36)与修正的Biot理论中的式(17)，可以发现，两个流体单元的运动方程并不一致(注意两者位移矢量的定义不一样)。陈龙珠认为上式的建立是以单位体积饱和土中的孔隙水作为研究对象的结果，若按照此观点，式中的pw应该为平均孔隙水压力(相当于s)。不过，即使如此，式(36)与Biot理论中的式(4)也是不一致的(忽略质量耦合项)。

可从以下两种不同的角度对上式进行修正。

(1) 将式(35)中的流体表观密度ρ2改为流体真密度ρw，则有

(37)

此时，对比式(37)与修正的Biot理论中的式(17)，尽管两式对孔隙水压力正方向的定义正好相反，但两式中孔隙水压力pw和pf的内涵是一样的，均是表示绝对孔隙水压力。在后续的引用中，仅需相应地在总应力表达式中对符号做出调整，也即，此时总应力表达式为σij=λξkkδij+2μξij+αpwδij。

夏唐代关于总应力边界条件表示为σz+pw=0(原文中定义固相应力σij=λξkkδij+2μξij，且假设土颗粒不可压缩，即α=1)，就属于上述情形。Tajuddin[23]中式(16)所定义的平均孔隙水压力s正方向与其文中的式(2)相反，而在后续的应力边界条件中却没有做出相应地调整。

(38)

上式两边同除以n，得：

(39)

以上分析也表明，因正方向和参数定义式的不同，或不同学者根据研究的需要，同一个方程可以有多种不同的表达形式，但万变不离其宗，只需在调用时相应地做出改变。

因此，在运用Biot理论或修正的Biot理论研究多孔介质中波的传播特性，尤其当因存在交界面而要使用应力边界条件时，要注意自身所定义的孔隙流体压力的正方向及其内涵，不能直接引用别人文献中的相关式子，否则在数值计算中将得不到正确的结果。

3.2其他参数

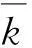
4结论

旨在探讨Biot理论与修正的Biot理论之间的关系，对其中易被混淆之处进行了分析，以便更好地理解和应用此理论，同时也希望对多孔介质土动力学研究的入门者会有所帮助。尽管Biot理论自建立至今已历经半个多世纪，如今对其进行比较及讨论仍然具有重要意义，因为双相孔隙介质Biot理论和修正的Biot理论是三相孔隙介质(如单孔隙非饱和多孔介质)和四相孔隙介质(如双重孔隙非饱和介质)土动力学分析的基础，同时在地震、勘探、交通等领域也有重要的工程应用价值。

参 考 文 献

[1] Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid.Ⅰ.Low frequency range [J]. Acoustical Society of America, 1956, 28(2): 168-179.

[2] Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid.Ⅱ. Higher frequency range [J]. Acoustical Society of America, 1956, 28(2): 179-191.

[3] Depollier C, Allard J F, Lauriks W. Biot theory and stress-strain equation in porous sound-absorbing materials [J]. Acoustical Society of America, 1988, 84(6): 2277-2279.

[4] Yang J. Importance of flow condition on seismic waves at a saturated porous solid boundary [J]. Journal of Sound and Vibration, 1999, 221(3): 391-413.

[5] 杨峻，吴世明，蔡袁强. 饱和土中弹性波的传播特性[J]. 振动工程学报，1996, 9(2):128-137.

YANG Jun, WU Shi-ming, CAI Yuan-qiang. Characteristics of propagation of elastic waves in saturated soils [J]. Journal of Vibration Engineering, 1996, 9(2): 128-137.

[6] Imomnazarov K K. Some remarks on the Biot system of equation describing wave propagation in a porous medium [J]. Applied Mathematics Letters, 2000(13):33-35.

[7] Santos J E, Corbero J M, Ravazzoli C L, et al. Reflection and transmission coefficients in fluid-saturated porous media [J]. Acoustical Society of America, 1992, 91(4): 1911-1923.

[8] 黄茂松，李进军. 饱和多孔介质土动力学理论与数值解法[J]. 同济大学学报:自然科学版，2004, 32(7): 851-856.

HUANG Mao-song, LI Jin-jun. Dynamics of fluid-saturated porous media and its numerical solution [J]. Journal of Tong-ji University:Natural Science, 2004, 32(7): 851-856.

[9] Biot M A, Willis D G. The elastic coefficients of the theory of consolidation [J]. Journal of Applied Physics, 1957, 24: 595-601.

[10] Claude Depollier, et al. Biot theory and stress-strain equations in porous sound-absorbing materials[J]. Acoustical Society of America, 1988, 84(6): 2277-2279.

[11] 李亮，赵成刚. 考虑质量耦合效应的流体饱和孔隙介质波动方程[J]. 固体力学学报, 2003, 24(2): 244-248.

LI Liang, ZHAO Cheng-gang. Equations of wave propagation with mass-coupling effect in fluid-saturated porous media [J]. Chinese Journal of Solida Mechanics,2003, 24(2): 244-248.

[12] 贺英. 流体饱和多孔介质弹性波方程正反演方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2009.

[13] 杨松岩，俞茂宏. 多相孔隙介质的本构描述[J]. 力学学报，2000, 32(1): 11-24.

YANG Song-yan, YU Mao-hong. Constitutive descriptions of multiphase porous media [J]. Chiness Journal of Thcoretical and Applied Mechanics,2000, 32(1): 11-24.

[14] Zienkiewicz O C, Shiomi T. Dynamic behaviour of saturated porous media; The generalized Biot formulation and its numerical solution [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1984, 8: 71-96.

[15] Degrande G, De Roeck G, Van Den Broeck P, et al. Wave propagation in layered dry, saturated and unsaturated poroelastic media [J]. Solids and Structures, 1998, 35:4753-4778.

[16] 徐平，夏唐代. 饱和度对准饱和土体中瑞利波传播特性的影响[J]. 振动与冲击，2008, 27(4): 10-14.

XU Ping, XIA Tang-dai. Influence of saturation degree on propagation characteristics of rayleigh waves in nearly saturated soils [J]. Journal of Vibration and Shock, 2008, 27(4): 10-14.

[17] 王立忠，吴世明. 波在饱和土中传播的若干问题[J]. 岩土工程学报，1995, 17(6): 96-102.

WANG Li-zhong, WU Shi-ming. Some aspects on wavepropagation in in saturated soil [J]. Chinese Journal ofGeotechnical Engineering, 1995, 17(6): 96-102.

[18] 陈龙珠，黄秋菊. 关于“波在饱和土中传播的若干问题”一文的讨论[J]. 岩土工程学报，1997, 19(1): 104-106.

CHEN Long-zhu, HUANG Qiu-ju. Discussion on“Some aspects on wavepropagation in in saturated soil” [J]. Chinese Journal of Geotechnical Engineering, 1997, 19(1): 104-106.

[19] 陈龙珠. 饱和土中弹性波的传播速度及其应用[D]. 杭州：浙江大学，1987.

[20] 陈龙珠，黄秋菊，夏唐代. 饱和地基中瑞利波的弥散特性[J]. 岩土工程学报，1998, 20(3): 6-9.

CHEN Long-zhu, HUANG Qiu-ju, XIA Tang-dai. Dispersion of rayleigh wave in a saturated soil ground [J]. Chinese Journal of Geotechnical Engineering, 1998, 20(3): 6-9.

[21] 夏唐代，陈龙珠，吴世明，等. 半空间饱和土中瑞利波特性[J]. 水利学报，1998, 2: 47-53.

XIA Tang-dai, CHEN Long-zhu, WU Shi-ming, et al. Characteristics of Rayleigh waves in a saturated half-space soil [J]. Journal of Hydraulic Engineering, 1998, 2: 47-53.

[22] 夏唐代，颜可珍，孙鸣宇. 饱和土层中瑞利波的传播特性[J]. 水利学报，2004(11): 81-84.

XIA Tang-dai, YAN Ke-zhen, SUN Ming-yu. Propagation of rayleigh wave in saturated soil layer [J]. Journal of Hydraulic Engineering, 2004(11): 81-84.

[23] Tajuddin M. Rayleigh waves in a poroelastic half-space [J]. Acoustical Society of America, 1984, 75(3): 682-684.

[24] Biot M A. Generalized theory of acoustic propagation in porous dissipative media [J]. Acoustical Society of America, 1962, 34(5): 1254-1264.

[25] Liu K, Liu Y. Propagation characteristics of rayleigh waves in orthotropic fluid-saturated porous media [J]. Journal of Sound Vibration,2004,271:1-13.