浮环式挤压油膜阻尼器减振机理研究

浮环式挤压油膜阻尼器减振机理研究

陈以彪，罗贵火

(南京航空航天大学能源与动力学院，江苏南京210016)

摘要：从广义雷诺方程出发，推导了浮环式挤压油膜阻尼器(FSFD)内、外层油膜的稳态雷诺方程。根据文中的理论模型，基于有限差分法编写了计算程序，研究分析了结构参数对FSFD动力特性的影响。研究表明：与传统SFD比较，FSFD改善了油膜力的非线性；相同条件下，FSFD内层油膜力要大于外层油膜力，内、外层油膜力都随油膜宽度的增大而增大，随油膜间隙的增大而减小；在结构参数一定的情况下，FSFD抑制突加不平衡的能力要强于传统SFD。

关键词:广义雷诺方程有限差分法浮环式挤压油膜阻尼器结构参数

中图分类号：V231.92文献标识码：A

作者简介：陈以彪，男，南京航空航天大学硕士研究生，研究方向：结构强度与完整性。

收稿日期：2014-12-20

Mechanism study of the floating-ring squeeze film dampers

CHEN Yibiao, LUO Guihuo

Abstract:In this paper, Reynolds equations of the inner and outer film of floating-ring squeeze film dampers(FSFD)are derived from the general Reynolds equation. A calculation program is written based on finite difference method and according to the theoretical model in the article. The influence of the dynamic characteristics is studied for FSFD about the structural parameters. The results show that Nonlinear is obviously improved by the FSFD compared with traditional SFD, and the inner film force is greater than the outer film force under the same conditions. Furthermore, both inner and outer film forces increases with the increase of oil film width, but decreases with the increase of oil film clearance. Under the condition of fixed structure parameters, the performance of FSFD is better than traditional SFD in preventing sudden unbalance response.

Keywords:general Reynolds equation; finite difference method; floating-ring squeeze film dampers; structure parameters

0引言

挤压油膜阻尼器(SFD)因结构简单、占用空间小、成本低、减振效果好等优点，广泛应用于高速旋转机械中。但由于SFD油膜力的高度非线性[1]，SFD-转子系统容易出现双稳态响应或非协调进动响应等现象[2-3]，进而引发转子系统产生较大振动甚至出现碰磨、疲劳等故障，限制了SFD的使用范围。为此，国内外学者提出了多种新型SFD，试图抑制或改善SFD由于油膜力高度非线性带来的危害。张世平、晏砺堂[4-5]研制了多孔挤压油膜阻尼器，能提高转子系统的不平衡承载能力以及工作的稳定性和可靠性，但由于小孔容易被堵塞，故未能在实际中得到应用。Hooshang Heshmat 和J.F. walton[6-7]等人研究设计了螺旋箔片多层挤压油膜阻尼器(SFMSFD)，能有效改善油膜刚度的高度非线性，但对制造工艺水平要求较高。俄罗斯学者设计了弹性环式挤压油膜阻尼器(ERSFD)，并将它成功地应用于多种现役的航空发动机上[8-9]。

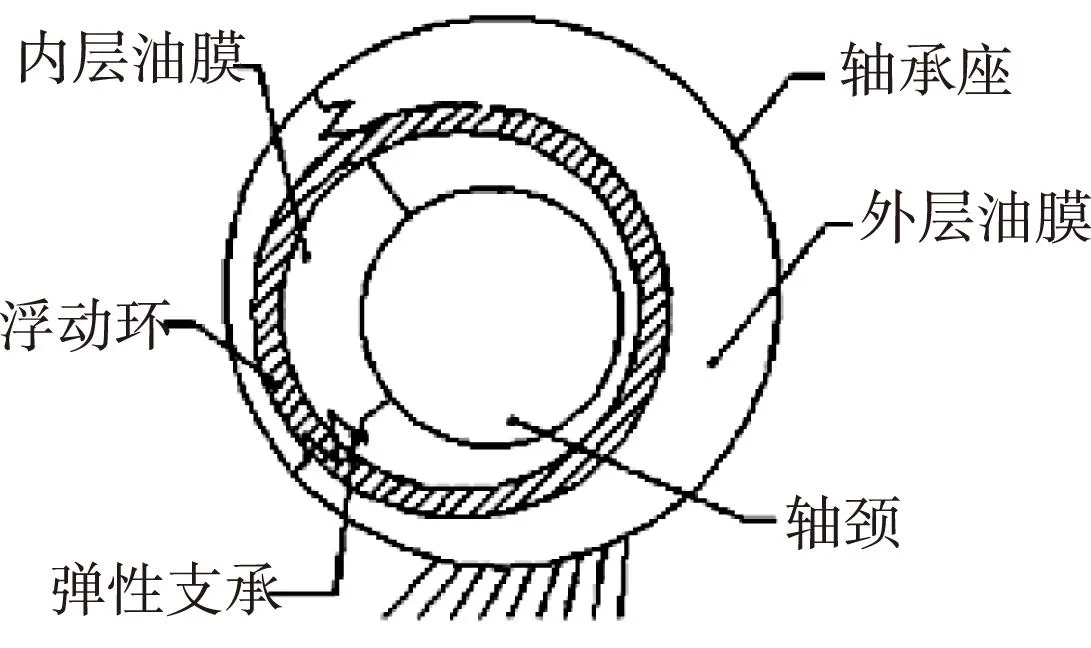
图1　浮环式挤压油膜 阻尼器结构简图

此外，还有分段式挤压油膜阻尼器(Segmented Dampers)、整体挤压油膜阻尼器(ISFD)、结构参数可控挤压油膜阻尼器(VPSFD)、金属橡胶阻尼器等[10-11]。这些新型SFD在某些方面改善了传统SFD的不足，但由于结构复杂或自身存在缺陷等方面的原因，未能在实际中广泛应用。本文对浮环式挤压油膜阻尼器(FSFD)进行了研究，FSFD结构简图见图1。

1内外层Reynolds方程的推导

取X轴沿轴切线方向，Y轴沿直径方向，Z轴为轴向，u、v、w，分别表示沿X、Y、Z方向的油膜流动速度，h为油膜厚度。假设油膜压力P沿Y方向不发生变化，油膜流动为层流，符合牛顿粘性定律，参考文献[1]，则三维可压缩流连续方程和运动方程可表示为：

(1)

(2)

边界条件：

当y=0时：u=U1，v=V1，w=0

当y=h时：u=U2，v=V2，w=0

对方程(2)沿0到h连续两次积分，代入方程(1)，结合边界条件，整理可得不可压缩流广义雷诺方程的极坐标表示：

(3)

1.1内层油膜Reynolds方程的推导

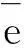
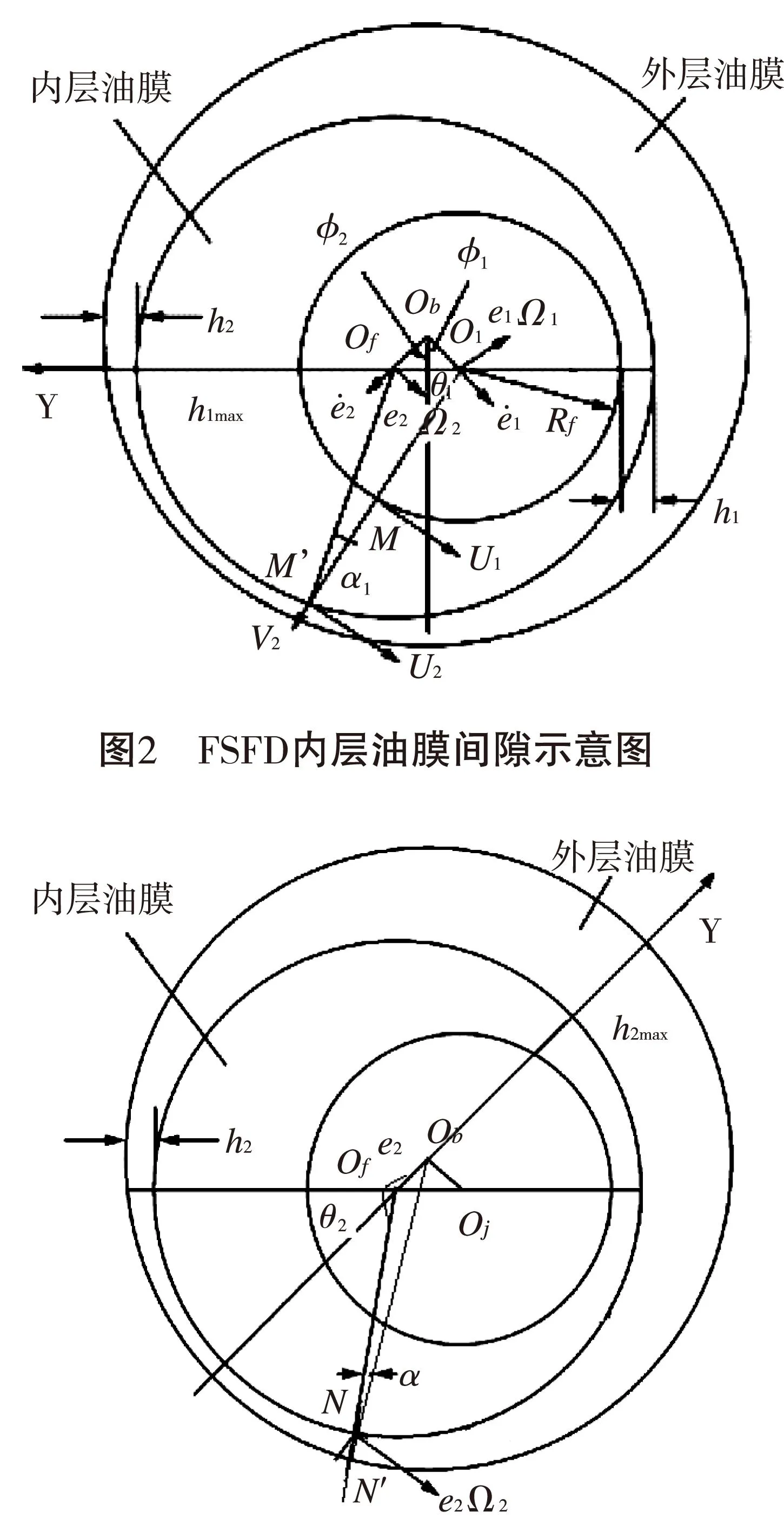
图3　FSFD外层油膜间隙示意图

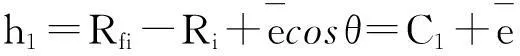
轴颈M点速度分量如下：

(4)

浮动环内表面M′点速度分量如下：

(5)

将式(4)和(5)代入式(3)可得内层油膜压力的Reynolds方程

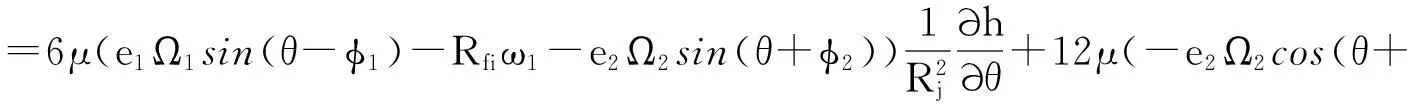
(6)

式中：vd表示内外层油膜上下两表面向外流动的流体净流速，θ、Z分别表示周向、周向坐标。

1.2外层油膜Reynolds方程的推导

参照图3，可近似得到外层油膜的油膜间隙为：

h2=Rb-Rfo+e2cosθ=C2+e2cosθ

N点和N′点沿浮动环外表面的切向速度及径向速度分量分别为U3、U4和V3、V4，油膜环静止，故：

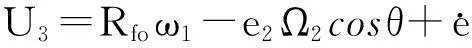
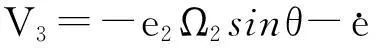
U4=V4=0

(7)

1.3浮动环自转转速的确定

参考壁面摩擦方程和Hirs整体流动理论[12-13]，则壁面剪应力为

τn，w=0.5ρun,wfn,w

式中的un、uw分别表示浮环内、外表面相对于内、外层油膜的流速，满足式：

un=[w2+(Rfiω1)2]1/2

uw=[w2+((1-ξ)Rfoω1)2]1/2

w=e1Ω1

式中，ξ为流速比，取为0.2；fn，w为摩擦参数，c1、c2、c3为Moody实验数值(c1=1.38×10-3，c2=2×104，c3=5×105)；en、ew分别为内、外表面粗糙度，en/h1=ew/h2=2×10-3。

稳定状态下，浮动环转速满足力矩平衡条件

∫02πτnRfidθ=∫02πτwRfodθ

(8)

由方程(8)可得出浮动环的自转转速。

2构造参数对FSFD油膜力特性的影响

根据前面推导的FSFD雷诺方程，基于有限差分法，构造求解油膜压力场的非线性Newton松弛迭代格式，结合短轴承半油膜边界条件，用MATLAB编写程序，从而求得内外层油膜压力分布。转子稳定运转时，轴颈进动速度与浮动环进动速度相等，为3 000rad/s，轴颈半径R=14mm，内、外层油膜间隙相等。初始条件下，间隙C=0.2mm，油膜宽度L=13mm，偏心率ε=0.1，滑油粘度μ=0.011 67Pa·s，进出口压力均为一个大气压。

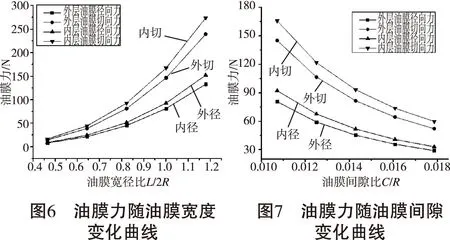
图4为初始参数下FSFD内、外层油膜力分布图，内层油膜力幅值要比外层油膜压力幅值大。图5为不同偏心率下，FSFD内、外层最大油膜压力沿周向坐标的变化曲线。图6和图7分别为内、外层油膜力随油膜宽度、油膜间隙的变化曲线。由图可知：

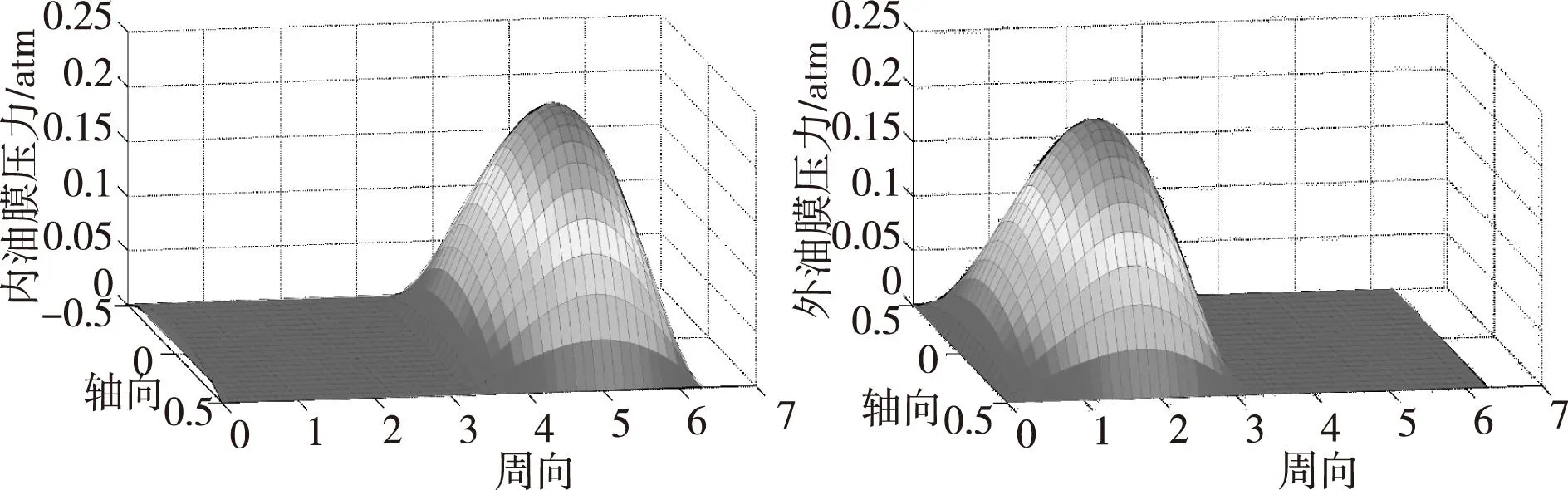
图4　偏心率ε=0.1时内外层油膜压力分布图

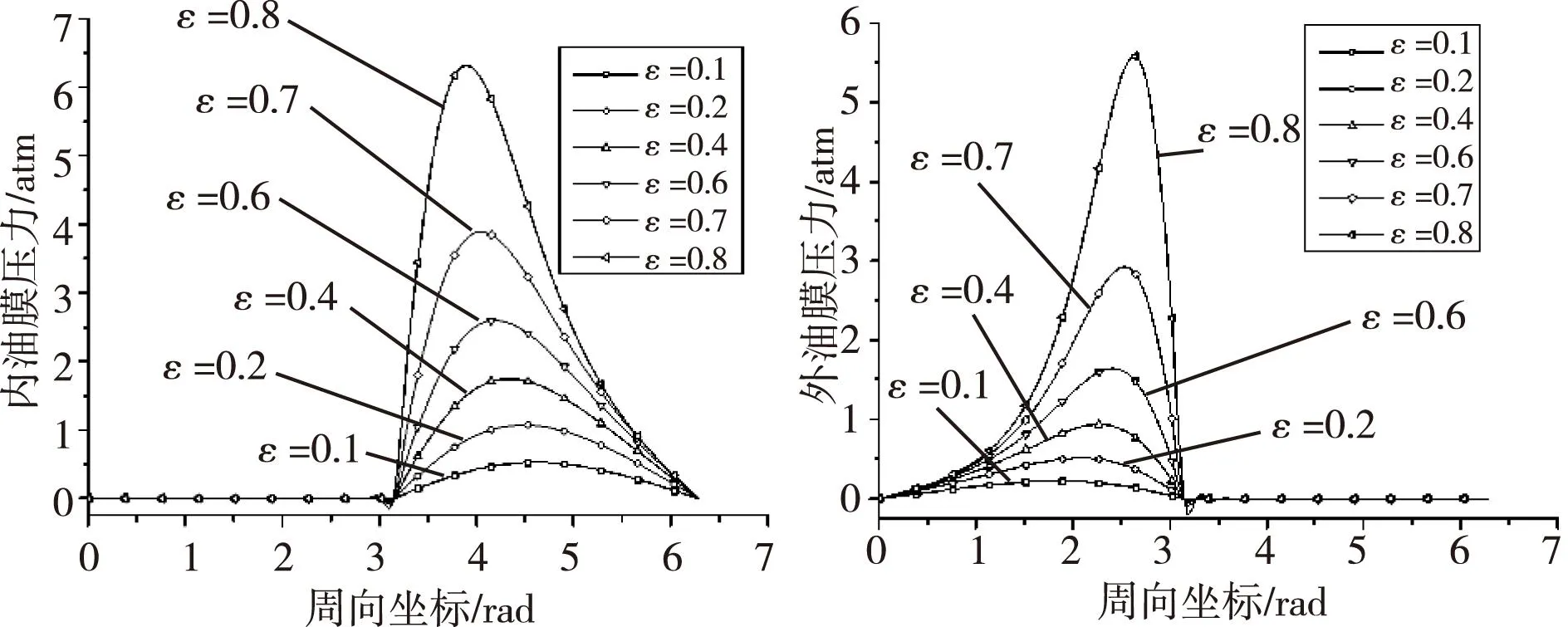
图5　不同偏心率下内、外层最大油膜压力沿周向变化曲线

1)随着偏心率ε的增加，FSFD内、外层最大油膜压力逐渐增大，即使在0.4≤ε≤0.6范围内，油膜压力增加的线性度仍然较好。而传统SFD在偏心率ε>0.4时，油膜力增加的非线性会很明显，故FSFD改善了油膜力高度的非线性，扩大工程适用范围，具有较好的应用前景。

2)在相同条件下，FSFD内层油膜径向力要大于外层油膜径向力，内层油膜切向力要大于外层油膜切向力；内、外层油膜的径向力、切向力都随油膜宽度的增大而增大，随油膜间隙的增大而减小。

3双向激励试验

FSFD内外层雷诺方程推导过程中作了一系列的假设，导致与实际工况有所不同，本文设计了双向激励试验器来模拟FSFD实际工况，采用进口的压力传感器测试了油膜压力，并将试验结果与计算结果进行对比分析。图8为双向激励试验简图，通过激振器对芯棒产生两个激励力，激励力幅值和频率相同，相角相差90°，模拟转子进动对油膜的挤压作用。

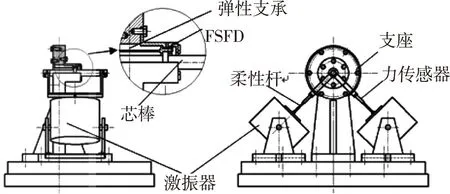
图8　双向激励试验装置简图

图9为油膜力随油膜间隙的变化曲线，试验时内外油膜间隙相同，从0.12 mm增加到0.22 mm。图10为油膜力随油膜宽度的变化曲线，油膜宽度从13 mm增加动33 mm。油膜压力试验测试结果与理论结果变化趋势大体一致，即油膜压力随油膜间隙的增加而减小，随油膜宽度的增加而增大。同时试验结果与计算结果的误差在10%以内，表明本文所建计算模型的正确性。

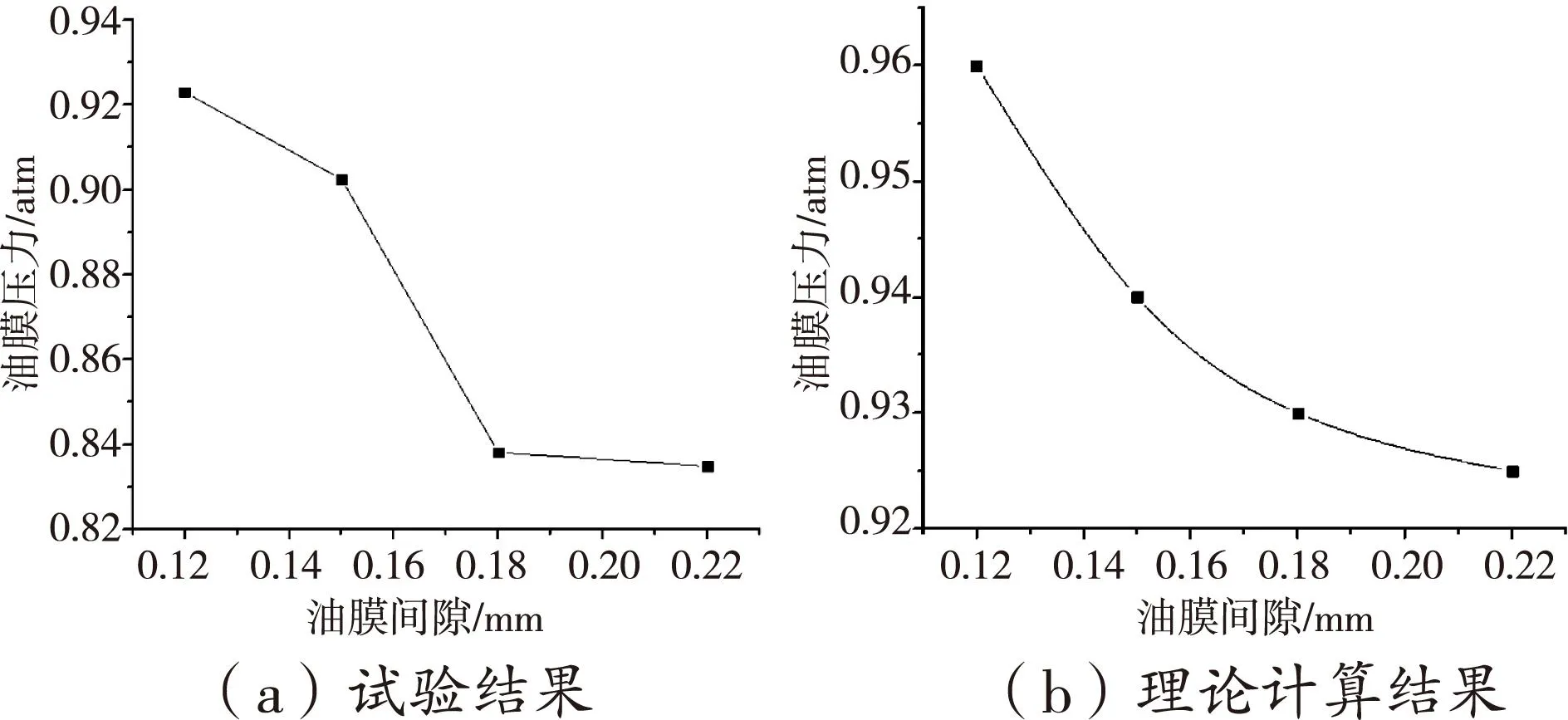
图9　油膜力与油膜间隙关系

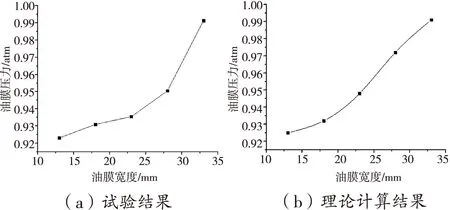
图10　油膜力与油膜宽度关系

4突加不平衡响应分析

为比较传统SFD与FSFD抑制转子系统突加不平衡能力，本文选取一个对称的Jeffcott转子模型，仿真计算了两种挤压油膜阻尼器转子系统在突加不平衡时的响应，并分析了转速对FSFD-转子系统突加不平衡响应的影响，结果见图11-13所示。

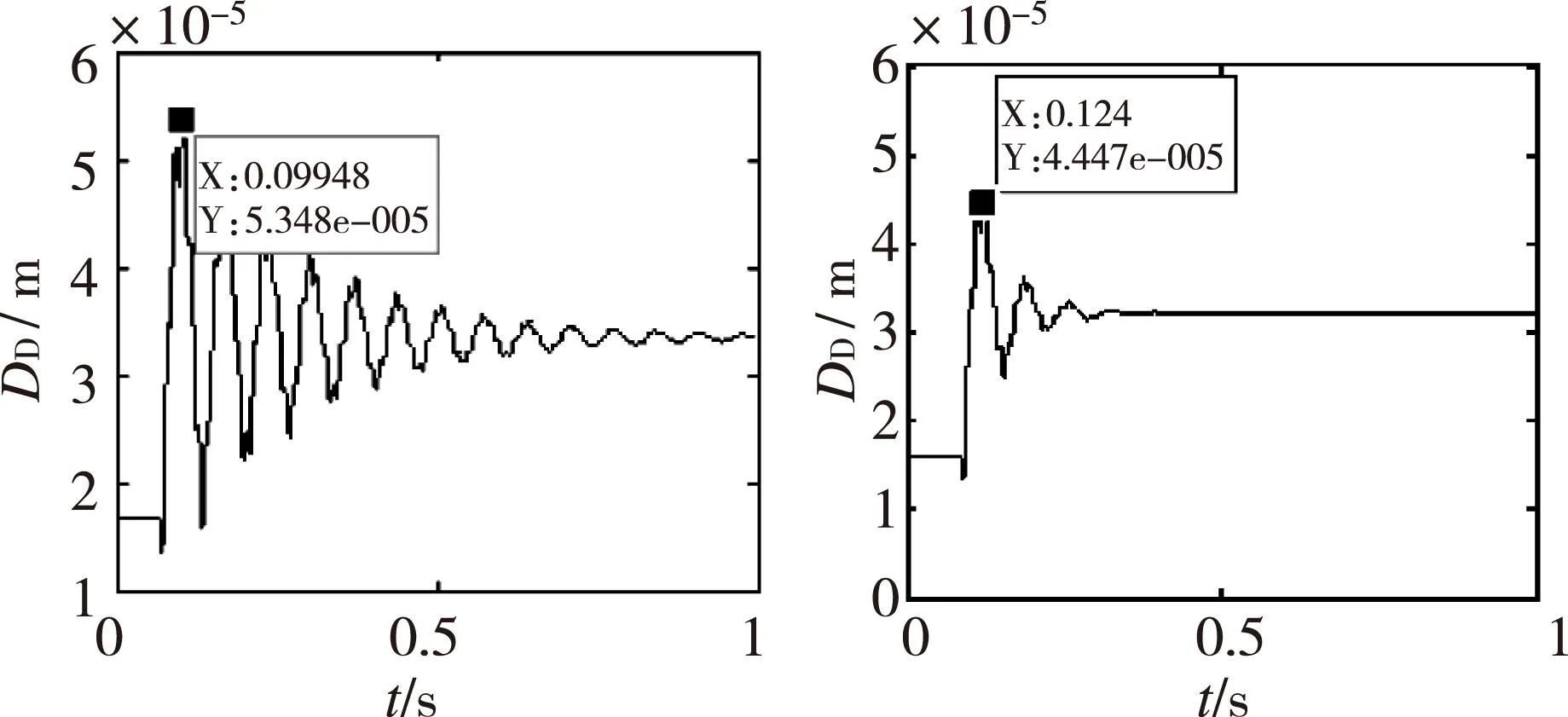
图11　SFD-转子系统突　　图12　FSFD-转子系统 　　　加不平衡响应　　　　　　突加不平衡响应

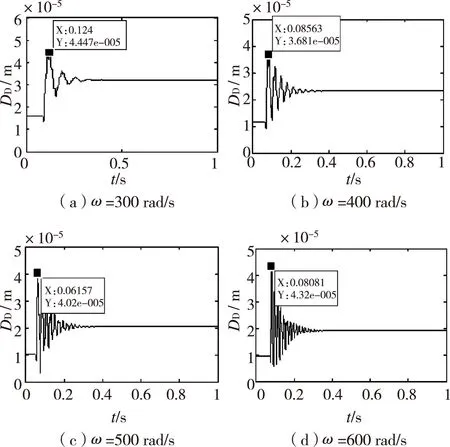
图13　不同转速下FSFD-转子系统突加不平衡响应

由图11和图12知，FSFD-转子系统的突加不平衡过程明显更短，瞬态幅值明显小。因此，与传统SFD相比，FSFD具有更强的抑制突加不平衡的能力。由图13知，随着转速的增加，FSFD-转子系统的突加不平衡瞬态幅值增大且瞬态过程变长。ω=300 rad/s时，接近转子系统的临界转速，故瞬态响应幅值较大。

5结束语

在考虑浮动环自转的情况下，基于广义雷诺方程，推导了FSFD内外层油膜雷诺方程。根据本文推导的理论模型，基于有限差分法编制了FSFD 油膜特性分析程序，研究分析了结构参数对FSFD动力特性的影响：

1)随着偏心率ε的增加，FSFD内、外层最大油膜压力逐渐增大，即使在0.4≤ε≤0.6范围内，油膜压力增加的线性度仍然较好。而传统SFD在偏心率ε>0.4时，油膜力增加的非线性会很明显，故FSFD改善了油膜力高度的非线性，扩大工程适用范围，具有较好的应用前景。

2)相同条件下，FSFD内层油膜径向力要大于外层油膜径向力，内层油膜切向力要大于外层油膜切向力；内、外层油膜的径向力、切向力都随油膜宽度的增大而增大，随油膜间隙的增大而减小。

3)设计了双向激励试验，测量FSFD油膜压力，试验结果与理论结果变化趋势是一致的，表明本文推导计算模型的正确性。试验结果均小于理论结果，误差在10%以内，可能是由于滑油在油管中流动损耗掉部分油压以及试验装置未完全密封引起的。

4)在结构参数一定的情况下，FSFD抑制突加不平衡的能力要强于传统SFD。随着转速的增加，FSFD-转子系统的突加不平衡瞬态幅值增大且瞬态过程变长。

参考文献

[1]周明, 李其汉, 晏砺堂. 弹性环式挤压油膜阻尼器油膜力特性研究[J]. 燃气涡轮试验与研究, 1998, (3): 17-23

[2]马艳红, 洪杰, 赵福安. 自适应挤压油膜阻尼器减振机理理论研究[J]. 北京航空航天大学学报, 2004, (1): 5-8

[3]曹磊, 高德平, 江和甫. 弹性环式挤压油膜阻尼器设计因素研究[J]. 燃气涡轮试验与研究, 2006, (4): 30-34

[4]张世平, 晏砺堂. 高效油膜阻尼器的研究与开发[J]. 航空动力学报, 1991,(2): 180-184

[5]晏砺堂, 张世平, 李其汉. 高效多孔环挤压油膜阻尼器的减振特性研究[J]. 航空动力学报, 1993, (3): 225-233

[6]H. Heshmat, J. F. Walton. Advanced multi-squeeze film dampers for rotor vibration control [J]. Tribology transactions, 1991, 34(4): 489-496

[7]J. F.Walton, H. Heshmat. Rotor dynamic evaluation of an advanced multi squeeze film damper-imbalance response and blade-loss simulation [J].Journal of Engineering for Gas Turbines and Power, 1993, 115(2): 347-352

[8]M. Leontiev.Damper supports[R].Samsung aerospace. Engine Research & Development Center, 1996

[9]Andres L S, Kim T H. Analysis of gas foil bearings integrating FE top foil models [J]. Tribology International,2009,42:111-120

[10]D.L.Taylor, & V.S.Fehr. Analysis and design of segmented dampers for rotor dynamic control[J].Journal of Lubracation Technology, 1982：104

[11]Zeidan, F.L. San Andrés, and J. Vance. Design and application of squeeze film dampers in rotating machinery [C]. Proceedings of the 25th Turbomachinery Symposium, Turbomachinery Laboratory, Texas A&M University, September, 1996:169-188

[12]孙启国, 姜培琳, 虞烈. 大间隙环流壁面摩擦及偏心转子静特性研究[J]. 摩擦学学报, 1999,19(3):261-265

[13]孙启国, 虞烈. 有限长大间隙环流中同心转子动特性系数研究[J]. 摩擦学学报,2001,21(6): 473-477