合成运动中三种运动概念的分析与运用

林茂　廖宇兰　罗洪峰　史留勇

摘要：针对学生学习点的合成运动中对三种运动概念分析理解存在的难度和疑惑，根据相关概念提出具体实例和机构动画，从而阐述三种运动的区别，进而采用极限法对速度合成定理及加速度合成定理进行分析和运用，使学生较好地理解和掌握合成运动知识点。

关键詞：合成运动；概念；合成定理；分析；运用

中图分类号：G642.0 文献标志码：A 文章编号：1674-9324（2016）04-0085-02

点的合成运动是理论力学中运动学篇的重点和难点内容，但学生对三种运动概念的理解不够深刻或者物体空间运动想象能力薄弱，对高等数学的矢量法、极限法、导数、微积分等知识掌握得不够牢固；同时，合成运动中概念较多，学生容易产生理解上的混淆[1，2]。本文通过阐述三种运动的概念与差异，进而运用相关定理来求解具体实例，力求达到学生较好地理解和掌握相关知识点。

一、基本概念分析

点的合成运动章节内容中的基本概念主要有：合成运动、定参考系、动参考系、绝对运动、相对运动、牵连运动、绝对轨迹、绝对速度、绝对加速度、相对轨迹、相对速度、相对加速度、牵连轨迹、牵连速度、牵连加速度等[3]。以下内容是针对难以理解的概念进行深入的剖析和探讨。

（一）点的三种运动概念分析

点的绝对运动和牵连运动概念学生一般容易理解，但是在对点的相对运动概念理解上则常常发生错误。例如图1中当物体M相对小车A的运动是直线运动或者垂直向上运动时，物体A相对物体M的运动是如何的？较多学生的理解为A相对M的运动是直线运动或垂直向下运动，这样的错误理解原因主要是没有把握住相对运动概念的本质。点的合成运动中三种运动的区分，首先要明确动点、动参考系和定参考系，即一点二系。相对运动即动点相对于动参考系的运动[3]，其概念的本质是动点在动系中的运动，这种运动是动系不动，动点是相对于动系的运动。所以要判断动点相对动系做何种形式的运动，就要先假设动系固定不动，然后观察动点在动系中的运动是何种形式的运动。在图1中的左侧，选择重物M为动点，小车A为动系，其相对运动形式的判断要先假设动系固定不动（即小车A不动），可以清晰观察到重物M在动系中的运动是垂直向上运动（直线运动），即动点在动参考系中的运动坐标是垂直向上运动的。若动点和动系的选择发生改变，即选择小车A为动点，重物M为动系，如图1右侧，那么动点相对于动系做何种形式的运动呢？此时要把握住相对运动概念的本质，动系固定不动，观察动点在动系的运动。从图1的右侧，动系M′不动，观察到动点A′的运动是水平直线运动，并没有出现多数同学所理解的相对运动是垂直向下运动。那么动点相对于动系的运动是水平直线运动吗？答案是否定的。原因是动点A′绝对运动是水平直线运动，若绝对运动和相对运动是同一个方向，则无法出现速度平行四边形合成定理，产生矛盾。因此，对此情况只能判断动点A′相对于动系M′的运动是未知的，即相对运动不明确。

（二）点的速度、加速度概念分析

对点的三种运动速度概念的理解和掌握，关键要明确点的三种运动轨迹，即绝对运动轨迹、牵连运动轨迹、相对运动轨迹。由运动轨迹去把握和理解相对应的运动速度。学生对绝对运动轨迹较为容易把握和理解，而对牵连运动轨迹和相对运动轨迹则较难把握和理解，进而导致对点的牵连速度和相对速度也较难理解。牵连运动轨迹不是动系相对定系运动的轨迹，而是动系上牵连点的运动轨迹。牵连点即为动点与动系相重合的点，是动系上的一点，具有瞬时性，动点在不同的瞬时对应于不同的牵连点[4]。

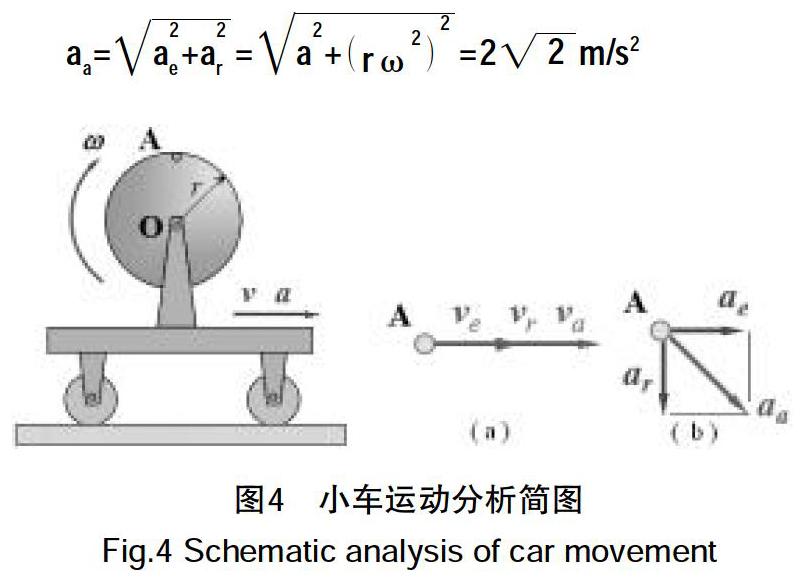
二、速度及加速度合成定理的运用

三、结语

上述针对点的合成运动的基本概念进行实例分析，能让学生更加容易地理解和掌握相关概念，重点分析了概念间的差异，也可以让学生意识到相关概念的正确理解要从源头开始追寻探索，有利于培养学生的思考能力。

参考文献：

[1]唐红春，王璐，史永高.理论力学点的合成运动体系教学探索及实践[J].江苏建筑职业技术学院学报，2014，14（1）.

[2]王斌耀，徐鉴.关于点的合成运动速度合成定理两种推导的辨析[J].力学与实践，2007，29（5）.

[3]哈尔滨工业大学理论力学教研组.理论力学[M].第7版.北京：高等教育出版社，2009：172-175.

[4]郝桐生.理论力学[M].第3版.北京：高等教育出版社，2003：270-273.