超弹性介电型EAP圆柱形驱动器变激励电压下动态响应分析

超弹性介电型EAP圆柱形驱动器变激励电压下动态响应分析

朱银龙1,王化明2,罗华安2, 3,周宏平1

(1. 南京林业大学机械电子工程学院,南京210037;2.南京航空航天大学机电学院,南京210016； 3.南京信息职业技术学院机电学院,南京210023)

摘要：超弹性电活性聚合物(electroactive polymer, EAP)圆柱形驱动器的动态特性是进行合理设计、使用及优化驱动器的重要依据。结合介电型EAP机电耦合方程，构建了驱动器轴向线性运动的动力学方程。通过计算得到驱动器的电压-轴向位移曲线，研究了驱动器在准静态点附近的稳定性。最后，分析了驱动器在施加阶跃和周期电压激励时的动态响应。结果表明，在有效工作范围内驱动器是稳定的，阶跃电压激励使驱动器在准静态点附近产生轴向振动，周期电压使驱动器产生包含自振的拟周期轴向振动。进一步分析表明，阶跃电压激励更易导致驱动器的电击穿失效。

关键词：超弹性 介电型EAP;圆柱形驱动器;动态响应

中图分类号:TP24

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.19.035

Abstract:The dynamic performance of a dielectric electroactive polymer (EAP) cylindrical actuator was a basis for its reasonable design, operation and optimization. Combined with the dielectric EAP electromechanical coupled equation, the dynamic equation for the axial linear movement of the actuator was deduced. The relation between the axial displacement of the cylindrical actuator and the applied voltage was obtained with the numerical solution to the dynamic equation, and the stability neigh bouring the quasi static point was analyzed. Finally, the dynamic responses of the actuator to applied step and periodic voltages were studied. The results showed that the actuator is stable in its effective working range, the sudden step voltage can cause the actuator’s axial vibration around the quasi-static position, and the periodic voltage generates its quasi-periodic axial vibration including its natural oscillation; furthermore, the sudden step voltage is easy to cause the actuator’s electric breakdown and damage.

Dynamic responses of a hyperelastic dielectric EAP cylindrial actuator under varying excitation voltage

ZHUYin-long1,WANGHua-ming2,LUOHua-an2,3,ZHOUHong-ping1(1. College of Mechanical and Electronic Engineering, Nanjing Forestry University, Nanjing 210037, China;2. College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;3. College of Mechanical and Electrical Engineering, Nanjing College of Information Technology, Nanjing 210023, China)

Key words:hyperelastic; dielectric electroactive polymer (EAP); cylindrical actuator; dynamic response

由于具有弹性变形大、能量密度高及重量轻等优点，EAP材料在驱动器应用方面的研究得到了广泛重视，并出现部分商业产品[1]。圆柱形驱动器[2-3]由EAP膜预拉伸后卷绕而成，内部由压缩弹簧支撑，通过对膜两侧表面的柔性电极施加电压，产生的静电压力使膜轴向拉应力减小，驱动器轴向伸长。圆柱形驱动器结构简单、能输出较大的位移和力，在力反馈设备、机器人手臂、仿生昆虫等方面具有应用前景[1-2, 4]。

静态特性是驱动器的基本特性，但驱动器的工作过程本质上是动态的，研究其动态特性是优化结构、合理应用的重要依据。采用非线性动力学研究超弹性薄膜动态响应受到研究者的关注[5-13], 任等[5-9]对超弹性薄膜的非线性动力学问题进行了较深入的研究，研究发现球壳在周期载荷下，当施加的平均载荷超过临界值时，在球壳中心会突然生成空穴并产生拟周期振动[5]；圆柱壳在动载荷作用下也存在易导致其破坏的临界值，且不动点与动态响应及运动性质存在关系[6]；球形薄膜在某些情形下周期振动的振幅会出现“∞”型同宿轨道以及周期振动的振幅会出现不连续增长现象[7]；另外，考虑到温度场下热传导因素，任等还对热超弹性圆柱壳[8]、球壳[9]的振动、破坏及稳定性问题进行研究。Goncalves等[10]分析了预拉伸率对超弹性圆形膜的振动频率、非线性幅频曲线、分岔图的影响。Zhu等[11-14]分析了介电型EAP单层圆形、筒形[12]、球形膜[13]在其两侧表面施加电压作用后动态响应问题，Yong还进一步分析了膜厚度对球壳稳定性的影响[14]，在文献[11]中Zhu还指出可通过改变周向固定的圆形薄膜的预拉伸率、内侧表面的压力、施加电压的值改变其自然频率。

上述文献仅涉及具有典型几何结构的单层薄膜在施加压力载荷(或电压)时的动态响应问题，但上述的圆柱形驱动器与这些典型结构是有区别的。为研究多层圆柱形驱动器施加电压后的动态响应，本文首先提出圆柱形驱动器的简化几何结构，在此基础上利用介电型EAP膜机电耦合方程建立了驱动器轴向位移的动力学方程，分析了超弹性介电型EAP驱动器在不动点处的稳定性。最后，对驱动器在施加阶跃及周期激励电压时的动态响应问题进行研究。

1圆柱形驱动器的简化结构

圆柱形驱动器[3]是由经过预拉伸的EAP膜在经过预压缩的弹簧外圈卷绕而成，在驱动器两端用端盖及热缩套管对EAP膜进行固定，膜的两面涂覆有柔性电极。电极涂覆区域一般称为活动(或主动)区域。当在EAP膜上施加电压时，弹簧的压缩力与EAP膜的预拉伸力平衡被破坏，驱动器产生轴向伸长变形。根据文献[3]对圆柱形驱动器静态特性分析结果，在卷绕层数不多、驱动器电压激励产生轴向变形不大的情况下，为简化分析可作如下假设：

(1)驱动器轴向伸长过程中，由于周向被固定，EAP膜只发生沿其轴向及厚度方向变形，各层EAP膜变形均匀一致；

(2)忽略EAP膜卷绕后周向侧边收缩变形对轴向拉力的影响；

(3)忽略EAP膜层间压力的影响。

于是，可将EAP圆柱形驱动器的活动区域简化为图1所示结构，该结构主要由经过预拉伸的矩形EAP膜和预压缩弹簧组成，D0为弹簧外径，EAP膜活动区域的初始几何尺寸为L1×L2×H。设在未施加电压，驱动器轴向力平衡时其周向及轴向预拉伸率分别为λp1和λp2。当驱动器EAP膜在电压U刺激作用下轴向伸长到λ2L2(λ2为EAP膜的轴向延伸率)时，其周向长度根据上述假设仍为L1λp1，而厚度变薄为H/(λ2λp1)。根据变形关系，设EAP膜在电场作用下产生的轴向延伸率为λza，则有λ2=λp2λza。

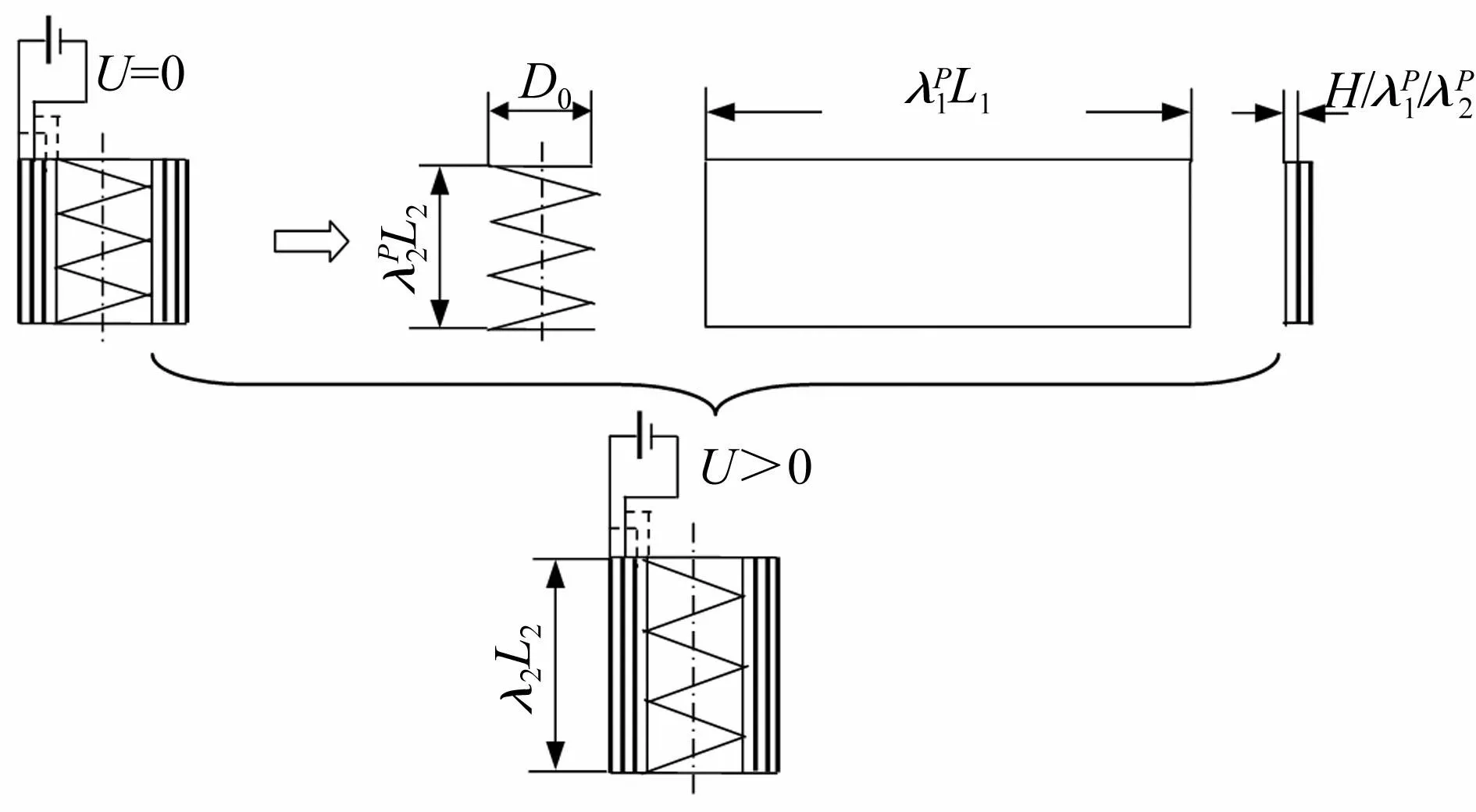
图1　圆柱形驱动器结构示意图 Fig.1 Structure schematic of o cylindrical actuator

2驱动器动力学方程

假设驱动器EAP膜材料为理想的超弹性介电型EAP[15]，则可采用neo-Hookean模型来描述其非线性超弹性应变。在电场作用下，EAP膜的周向应力σ1、轴向应力σ2、径向应力σ3有如下关系[12]

(1)

式中，ε=ε0εr，ε0为真空介电常数，εr为EAP材料的相对介电常数；λ1、λ2、λ3为图1中驱动器EAP膜的周向、轴向和径向延伸率，且λ1=λp1、λ3=1/λ1/λ2；E=λ1λ2U/H为电场强度；μ为材料的剪切模量。

当忽略驱动器卷绕层之间的压力时，可得边界条件σ3=0。根据式(1)可求得σ1和σ2，并可求得在电压激励作用下，EAP膜轴向弹性力Fela为

Fela=σ2L1H/(λp2λza)

(2)

圆柱形驱动器采用轴向预压缩的压缩弹簧提供预载荷。假设弹簧为线性恒刚度弹簧，则其轴向弹性回复力Fs为

Fs=Fp-kspringλp2L2(λza-1)

(3)

式中，kspring为弹簧刚度；Fp为弹簧预压缩力。

驱动器未通电时，EAP膜的轴向弹性力Fela与Fp相等，即式(2)中当U=0，λza=1时Fela的值，故实际计算Fp时也可按下式确定

(4)

施加电压后驱动器伸长实际上是压缩弹簧克服EAP膜的弹性阻力而发生轴向位移的过程。根据牛顿第二定律，其轴向位移的动力学方程为

Fs-Fela=kmFm

(5)

式中，Fm为膜活动部分(即涂覆电极部分)质量惯性力；km为折算系数，主要考虑弹簧、固定端盖及膜的非驱动部分等附加质量引起的惯性力。驱动器活动部分薄膜的惯性力

(6)

式中，me=2ρL1L2H为活动部分(双层)膜的质量。于是，驱动器轴向运动方程可简化

(7)

(8)

3驱动器空载时准静态平衡位置分析

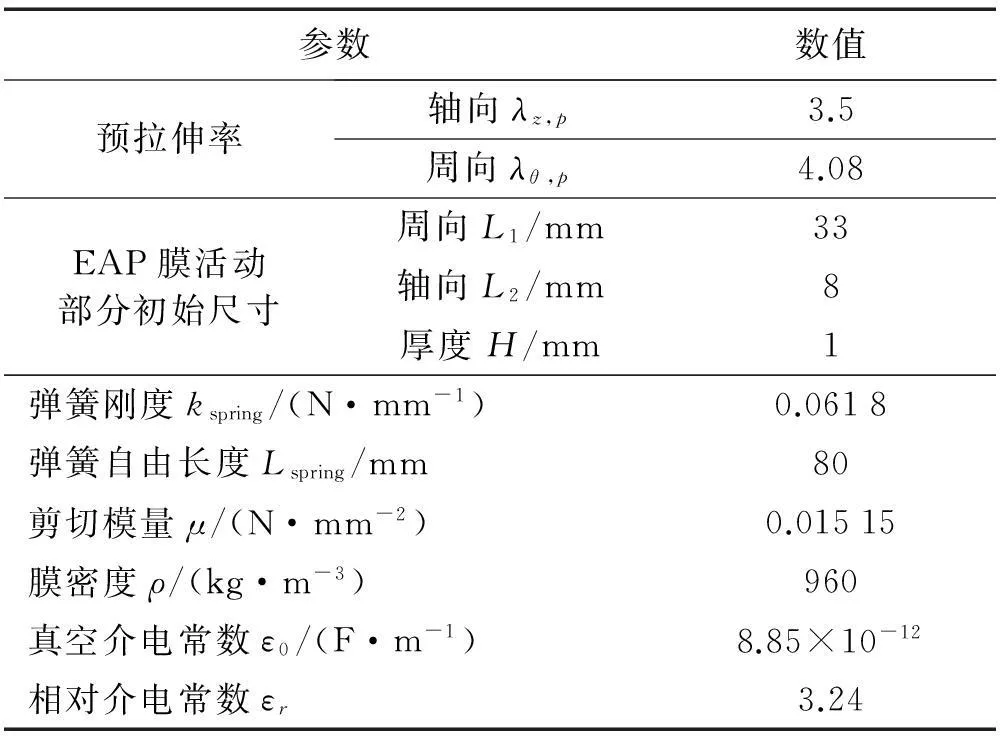
表1　圆柱形驱动器参数值

注：剪切模量μ由等轴拉伸试验[16]数据拟合获得

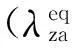
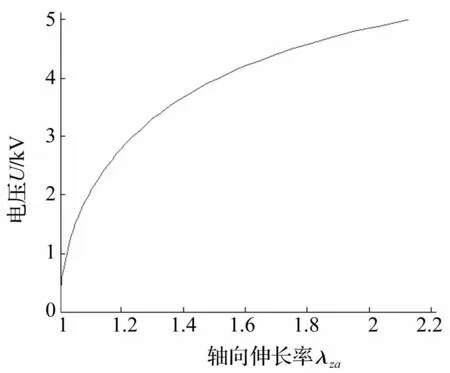
图2　驱动器准静态电压-位移曲线 Fig.2 Quasi-static curve of voltage and displacement for actuator

(9)

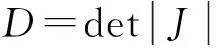
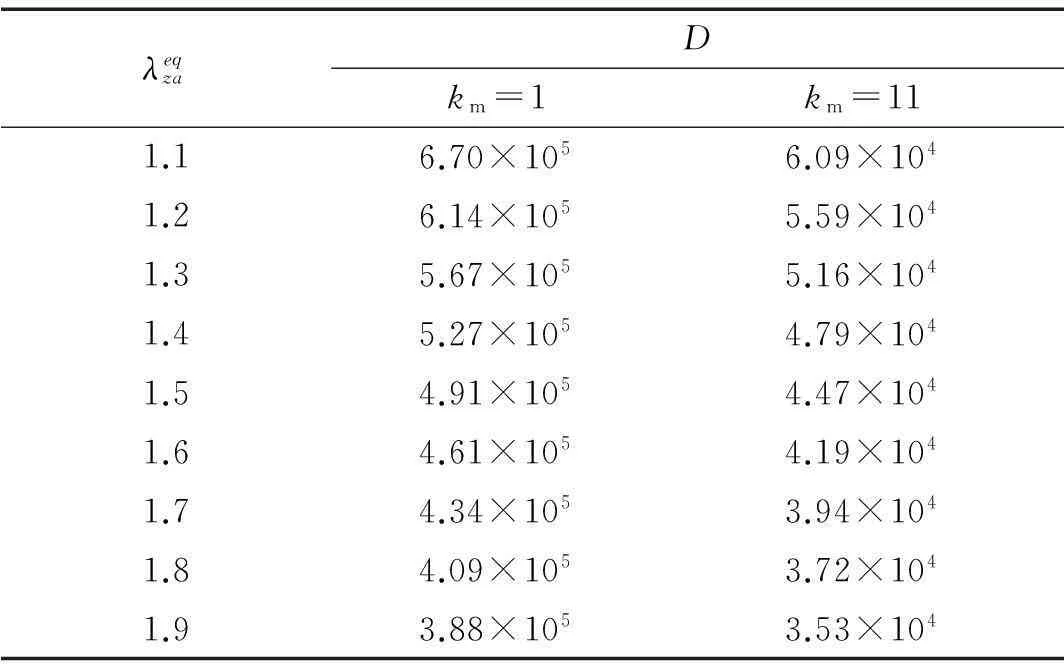
表2　Jacobi矩阵的值

4驱动器的动态响应

圆柱形驱动器施加电压后的轴向伸长是一个动态过程，本文仍以表1所列参数为例来分析超弹性EAP圆柱形驱动器在施加阶跃及周期电压激励时的动态响应。

4.1施加阶跃电压时的动态响应

(10)

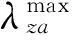
图中计算得到的λza-υλ曲线为封闭“椭圆形”曲线，准静态平衡点为其中心。于是，可认为基于上述理想的几何模型，当在圆柱形驱动器EAP膜上施加阶跃电压时，驱动器会产生绕其准静态平衡点的轴向周期振动；进一步分析可知，激励电压越高其轴向伸长率及伸长速率越大。对照图3(a)及3(b)，附加质量会减小驱动器最大伸长速率，但对轴向伸长率幅度无影响。由于采用可变预载荷，驱动器虽没有发生失稳现象，但振幅会使EAP膜的最大工作电场超过其电击穿强度。因此，考虑到EAP膜的电击穿，实际驱动器的最大工作电压比准静态计算得到的最大工作电压要低。

图3　驱动器轴向位移运动相图 Fig.3 Phase diagram for axial displacement of actuator

4.2施加周期电压时的动态响应

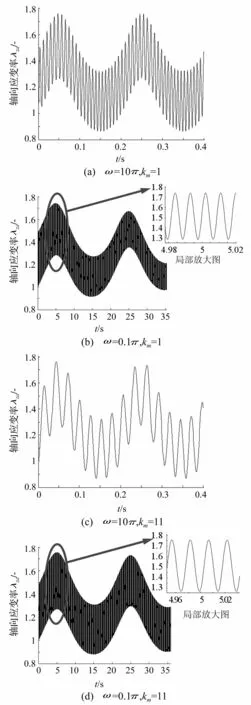
图4　U 1=3 kV, U 2=1 kV时驱动器轴向位移时程曲线 Fig.4 Axial displacement time history curve of actuator (U 1=3 kV, U 2=1 kV)

研究当施加形如U(t)=U1+U2sin(ωt)的周期电压时驱动器的轴向位移动态响应，可对上式采用Runge-Kutta法进行数值积分，U1、U2分别为周期电压的直流电压分量及正弦电压分量的幅值。图4、图5分别列出了当周期激励电压的最大幅值相同(即U1、U2之和相同)情况下，ω=0.1π及ω=10π时，驱动器轴向位移的时程曲线。

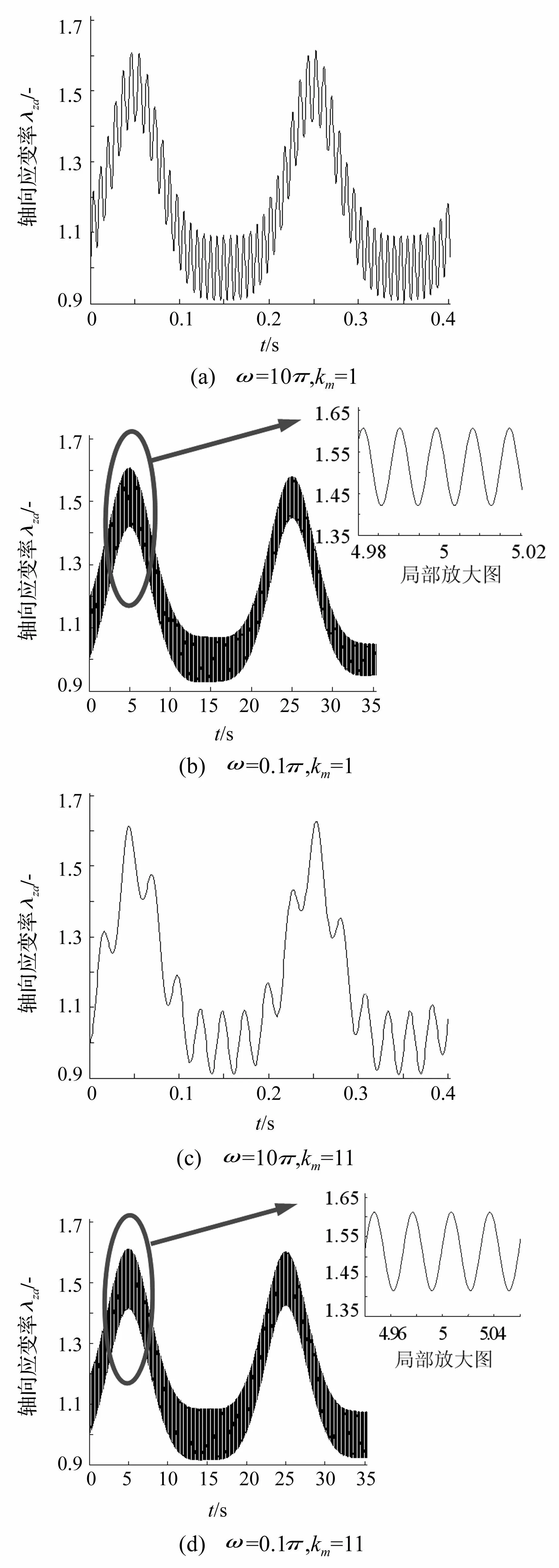
图5　U 1=2 kV, U 2=2 kV时驱动器轴向位移时程曲线 Fig.5 Axial displacement time history curve of actuator (U 1=2 kV, U 2=2 kV)

由图可知，在施加周期电压时，驱动器的轴向位移运动是拟周期振动，可认为是由自振和强迫振动叠加而成。附加质量影响自振频率，强迫振动频率取决于周期电压的频率ω。由于自振的存在，驱动器轴向振动时，膜的最大延伸率会超过其相应恒值直流电压激励产生的变形；同时，当周期激励电压的瞬时电压为(或接近)0V时，EAP膜最小延伸率会小于1(λza<1)。

通过计算可知，驱动器轴向位移幅度主要受U1、U2值的影响。虽然U1、U2之和相同(4 kV),但直流分量U1越大则驱动器的轴向位移幅度越大，越易导致膜电击穿。当U1= 3kV、U2=1 kV时，其最大轴向伸长λza可达1.76；而当U1=2 kV、U2=2 kV时，膜的最大轴向延伸率λza只有1.61，比上述小10%左右。另外，从图5可知，当周期电压波谷值接近0 V时，驱动器轴向拟周期振动呈现波谷平坦，而波峰尖锐的特征，这对避免EAP膜的电击穿是有利的。

因此，从电击穿角度来讲，突加恒值激励电压易使驱动器发生电击穿失效。一般来讲，黏性会对振动有一定的抑制作用，为方便分析，上述论述中采用具有黏性的VHB4910膜作为超弹性EAP材料的参数进行理论计算，这在具有分析时需引起注意。

5结论

本文通过构建超弹性EAP圆柱形驱动器的动力学方程，分析了其在准静态平衡点附近的稳定性问题，并对其动态响应进行研究，得到如下结论：

(1) 由于圆柱形驱动器采用变载荷的预加载形式，施加电压后驱动器不会发生机电失稳，但EAP膜的电击穿失效会限制其电压许用范围。

(2) 驱动器的附加质量主要影响其最大伸长速率及自振频率，在一定伸长范围内不影响驱动器的稳定性，对其轴向位移幅值影响也不明显。

(3) 施加形如U(t)=U1+U2sinωt的周期激励电压，在U1、U2之和相同时，其直流分量(U1)越大，驱动器轴向振动最大幅值也越大；增加其交流分量幅值U2，会产生波谷平坦的非对称拟周期振动，在瞬时电压0 V附近出现λza<1。

(4)相对于周期电压，阶跃电压激励更易导致驱动器EAP膜的电击穿失效。

参考文献

[1]Carpi F, De Rossi D, Kornbluh R, et al. Dielectric elastomers as electromechanical transducers[M]. Amsterdam: Elsevier, 2008.

[2]Kovacs G, Lochmatter P, Wissler M. An arm wrestling robot driven by dielectric elastomer actuators[J]. Smart Structures and Materials, 2007, 16(2): 306-317.

[3]罗华安, 王化明, 游有鹏. 介电弹性体圆柱形驱动器静态特性分析[J].农业机械学报, 2012，43(9): 202-208.

LUO Hua-an, WANG Hua-ming,YOU You-peng. Static characteristic of dielectric elastomer cylindrical actuator[J]. Transactions of the Chinese Society for Agricultural Machinery, 2012，43(9): 202-208.

[4]Zhang Rui, Kunz Andreas, Lochmatter P, et al. Dielectric elastomer spring roll actuators for a portable force feedback device[C] // 14th Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems, Virginia, USA: IEEE Computer Society, 2006: 347-353.

[5]任九生, 沈佳铖, 袁学刚. 周期载荷下不可压超弹性材料的空穴动生成[J]. 振动与冲击, 2012,31(18):10-13.

REN Jiu-sheng, SHEN Jia-cheng, YUAN Xue-gang. Dynamical Cavitation for an incompressible hyper-elastic material sphere under periodic load[J].Journal of Vibration and Shock, 2012,31(18):10-13.

[6]Ren Jiu-sheng. Dynamical response of hyper-elastic cylindrical shells under periodic load[J]. Applied Mathematics and Mechanics, 2008, 29(10): 1319-1327.

[7]袁学刚，张洪武，任九生,等. 动载荷下不可压缩超弹性球形薄膜的若干定性性质[J]. 应用数学和力学，2010, 31(7)：860-867.

YUAN Xue-gang, ZHANG Hong-wu, REN Jiu-sheng, et al. Some qualitative properties of incompressive hyperelastic spherical membranes under dynamic loads[J].Applied Mathematics and Mechanics, 2010, 31 (7): 860-867.

[8]任九生. 热超弹性圆柱壳的振动与破坏[J]. 振动与冲击, 2008,27(12):36-39.

REN Jiu-sheng.Finite oscillation and destruction of thermo-hyperelastic cylindrical shells[J].Journal of Vibration and Shock,2008,27(12):36-39.

[9]任九生, 程昌钧. 受内压热超弹性球壳的不稳定性[J]. 上海大学学报:自然科学版，2007，13(6)：732-735.

REN Jiu-sheng, CHENG Chang-jun. Instability of inflated incompressible thermo-hyperelastic spherical shells[J]. Journal of Shanghai University:Natural Science, 2007, 13(6): 732-735.

[10]Goncalves P B, Soares R M, Pamplona D. Nonlinear vibrations of a radially stretched circular hyperelastic membrane[J]. Journal of Sound and Vibration,2009,327(1/2):231-248.

[11]Zhu Jian, Cai Sheng-qiang, Suo Zhi-gang. Resonant behavior of a membrane of a dielectric elastomer[J]. International Journal of Solids and Structures, 2010,47: 3254-3262.

[12]Zhu J, Stoyanov H, Kofod G, et al. Large deformation and electromechanical instability of a dielectric elastomer tube actuator[J]. Journal of Applied Physics, 2010,108:074113.

[13]Zhu Jian, Cai Sheng-qiang, Suo Zhi-gang. Nonlinear oscillation of a dielectric elastomer balloon[J]. Polym Int, 2010, 59: 378-383.

[14]Yong Hua-dong, He Xin-zhen, Zhou You-he. Dynamics of a thick-walled dielectric elastomer spherical shell[J]. International Journal of Engineering Science, 2011,49:792- 800.

[15]Zhao Xuan-he, Wei Hong, Suo Zhi-gang. Electromechanical coexistent states and hysteresis in dielectric elastomers[J]. Physical Review B, 2007, 76: 134113.

[16]罗华安,王化明, 游有鹏,等.超弹性膜的等轴拉伸试验方法及仿真[J]. 华南理工大学学报:自然科学版, 2011,39(4):56-61.

LUO Hua-an, WANG Hua-ming, YOU You-peng, et al. Experimental methods of equiaxial tension of hyperelastic membrane and corresponding simulations[J]. Journal of South China University of Technology:Natural science edition, 2011, 39(4): 56-61.

[17]Medhat A, Besada A. Developing spring-roll dielectric elastomer actuator system based on optimal design parameters[J/OL]. IJCSI International Journal of Computer Science Issues,2011, 5(8), No 2, ISSN: 1694-0814. http://www.IJCSI.org.