改进多尺度法求解环形极板机电耦合强非线性系统主共振的研究

改进多尺度法求解环形极板机电耦合强非线性系统主共振的研究

杨志安1，李熙2,孟佳佳3

(1.唐山学院唐山市结构与振动工程重点实验室，河北唐山063000； 2.天津大学机械工程学院，天津300072； 3.河北联合大学机械工程学院，河北唐山063009)

摘要：研究环形极板机电耦合系统的强非线性问题。按照弹性力学理论建立环形极板机电耦合系统的动力学方程，利用Galerkin方法将其转化为非线性振动方程。转化后的振动方程是杜芬-马修方程，有两个外激频率。应用多尺度法求得系统的主共振的幅频响应曲线，分析了不同的系统参数对共振的影响。

关键词：环形极板机电耦合系统；改进多尺度法；强非线性；简谐激励；主共振

中图分类号:O322

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.19.033

Abstract:In order to study primary resonance of an annular plate electromechanical coupled strong nonlinear system, the nonlinear dynamic equation of the system was established by applying the elastic theory. The nonlinear oscillation equation was obtained based on Galerkin’s method. It was a Duffing-Mathieu equation with two external excitation frequencies. The approximation solutions to the primary resonance of the system were gained with the improved multi-scale method. The influences of different system parameters on the primary resonance of the system were analyzed in detail.

Improved multi-scale method for primary resonance of an annular plate electromechanical coupled strong nonlinear system

YANGZhi-an1,LIXi2,MENGJia-jia2(1. Tangshan Municipal Key Laboratory of Structure and Vibration, Tangshan College, Tangshan 063000, China;2. School of Mechanical Engineering,Tianjin University,Tianjin 300072,China; 3. College of Mechanical Engineering, Hebei United University, Tangshan 063009, China)

Key words:annular plate electromechanical coupled system; improved multi-scale method; strong nonlinear; harmonic excitation; primary resonance

机电耦合系统广泛存在于工农业生产和科学技术领域，在国民经济发展中占有重要的地位[1]。环形板在工程中有广泛的应用，在一些空间立体结构、电子元器件、和旋转机械等都可以看到环形板的存在。微电子机械系统中的环形极板机电耦合系统属于典型的机电耦合系统。将环形板应用到机电耦合系统中有一定的优点。在机电耦合系统中环形薄板内外边缘都可以固定，相对于微梁和圆薄板具有稳定性好，可操作性高等优点。关于环形板的研究已经有一些成果。love[2]首次尝试解决圆环平面振动的问题，推到出了环形薄板在自由边界条件下的运动方程和通解。Irie等[3]利用矩阵的传递公式计算了环形板不同边界条件下在平面内振动的固有频率，但是不同边界条件对应的振型没有给出。Ambati等[4]提出了环形板平面振动分析一般化的公式，对于圆盘和圆环都适用，作者还通过试验对分析结果进行了验证。Arafat等[5]研究了边界固定环形板在轴对称的热载荷作用下的非线性强迫振动，结合冯·卡门板的方程和热传导方程描述系统的运动，利用解析和数值的方法分析了环形板在主共振附近的一个模态在简谐激励下的振动。 Arafat等[6]研究了受热载荷以及边界固定条件下的环形板在一阶和二阶轴对称模态之间发生三分之一内共振时的强迫振动，考虑环形板内部受轴对称热载荷，外部受到二阶模态主共振附近简谐力的激励，利用冯·卡门板的方程描述系统的振动，应用多尺度法研究系统的响应，发现两种模态下系统会发生周期振动，其中大部分周期振动来自一阶模态，另外周期解会经历Hopf分岔从而导致环形板发生非周期振动。

系统的主共振是不考虑系统动力学方程中参数项的影响，令外部激励的频率与系统的固有频率相接近而引起的共振现象。系统在主共振情况下同样具有复杂的动力学现象,熊蕊等[7]研究了含PID控制器的迟滞非线性闭环控制系统在简谐激励下的主共振，利用奇异性理论对分岔方程进行了分析，得到了转迁集和分岔图，并分析了系统参数对开折参数和分岔参数的影响。本文研究环形极板机电耦合强非线性系统在简谐激励下的主共振问题。

1环形极板机电耦合系统基本方程

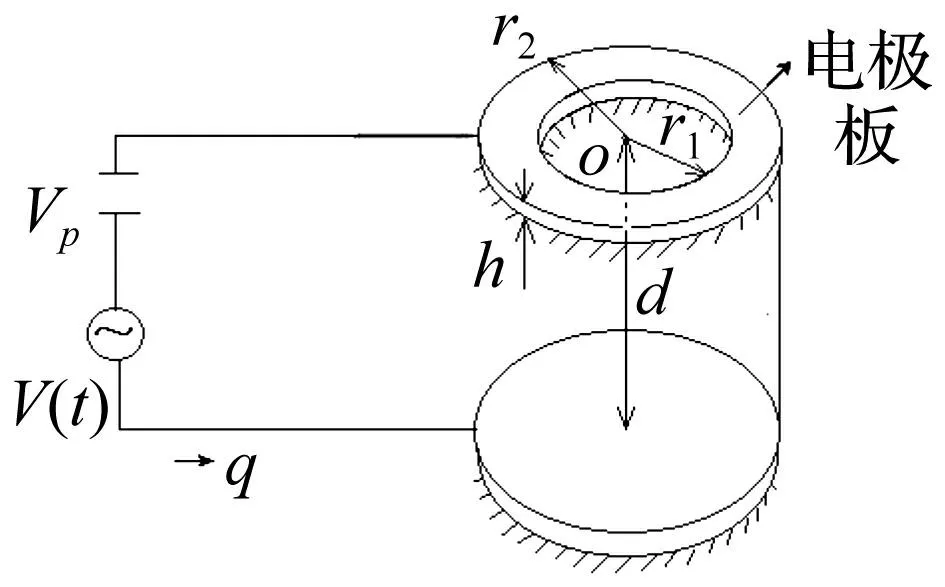
图1　静电驱动环形极板耦合模型 Fig.1 Model of coupled annular plate actuated by an electric load

见图1，环形电容器在电路中的模型。在轴对称情况下，考虑圆环的内半径为r1，外半径为r2，厚度为h，阻尼系数为c，面密度为ρ，该圆环有横向均匀分布的对称载荷电磁力F。由F激起的轴对称振动模式，其基本方程为动力学冯·卡门偏微分方程，即：

(1)

(2)

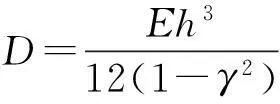
电容器的环形极板，假定内外边缘为固定加紧。即边界条件为：

(3)

应用伽辽金法求解非线性振动控制方程，将挠度函数进行时间与空间的分离，即设定环形极板的瞬间挠度为：

W(ξ,t)=hx(t)w(ξ)

(4)

式中：h为环形电容器极板的厚度，x(t)是关于时间t的无量纲函数，由振动控制方程给出。在轴对称横向均匀载荷电磁力F的激励下，设w(ξ)为无量纲的偶数项幂函数，即

w(ξ)=c0+c2ξ2+c4ξ4+c6ξ6+ξ8

(5)

将式(5)代入式(4)，在进行求导运算得：

由环形极板边缘固定夹紧的边界条件得：

(7)

式中的环形极板厚度h与关于时间的x(t)均为无量纲函数，两者都不能恒为零，在极板外边缘固定时，即在ξ=1时有：

(8)

同理考虑环形极板内边缘固定(ξ=0.41)时边界条件：

(9)

联立式(8)和式(9)解得：

c0=0.0283；c2=-0.3927；c4=1.7007；c6=-2.3362。

将c0、c2、c4、c6的值代入式(2)整理可得：

(10)

解上式可得：

(11)

将式(4)、式(5)和式(11)代入式(1)得：

(12)

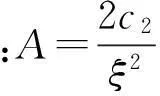
应用伽辽金法消除残余值得：

(13)

计算上式可得：

(14)

等式(14)右端的交变电压为：v(t)=v0sinω1t(式中v0为交变电压的幅值，ω1为交变电压的频率)，则有：

(15)

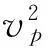
(16)

其中等号右端分母可以由泰勒级数进行展开为：

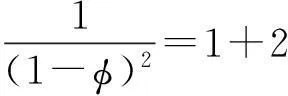
(17)

将式(17)代入式(16)整理可得：

2η2sinω1t)u(t)+(3η1cos2ω1t-

3η2sinω1t)u2(t)+(η3+4η1cos2ω1t-

4η2sinω1t)u3(t)=-η1cos2ω1t+η2sinω1t

(18)

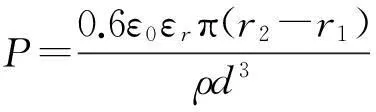
2环形极板机电耦合系统主共振理论分析

通过代入数据可知，非线性项系数的数量级比线性项系数的数量级大，可以确定静电驱动下环形极板机电耦合模型数学方程(18)为强非线性方程，且有两个不同的外激频率。下面研究主共振的定常运动方程，不考虑参数项的影响，在阻尼项、杜芬项和激励项前引入非小量参数ε得系统的振动方程为：

4η2sinω1t)u3-η1cos2ω1t+η2sinω1t]

(19)

令：

(20)

引入参数变换：

(21)

则有：

(22)

将小参数α引入到多尺度方法中，设方程(19)的一次渐近解为：

u(t,α)=u0(T0,T1)+αu1(T0,T1)+…

(23)

式中：T0=t，T1=αt。

将式(22)、(23)代入方程(19)且比较α同次幂的系数，得到一组线性偏微分方程：

(24)

(25)

式(24)的解为：

(26)

式中：

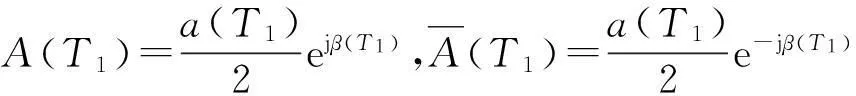
(27)

将式(26)代入式(25)可以得到消除长期项的条件为：

(28)

式中：

(29)

将式(27)、(29)代入式(28)，整理可得：

(30)

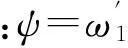
(31)

3数值计算及结果分析

参考文献为了定量求解给各个参数赋值。电容器环形极板取值[8-9]，极板内外边缘固定且ξ=0.41，具体值为：E=200GPa，γ=0.27，ρ=2300kg/m`3，c=1.2kg·m/s`3，h=1.5 μm，d=85μm，r2=760μm，v0=3V，vp=3V， ε0=8.85×10`(-12)，εr=1。按式(31)用Matlab语言可以计算系统不同参数的幅频响应曲线，分析系统参数对幅频响应曲线的影响。

图2～图6为系统主共振不同参数下的幅频响应曲线，可以看出他们具有单共振峰，且向右倾斜，呈现系统的硬特性特征。

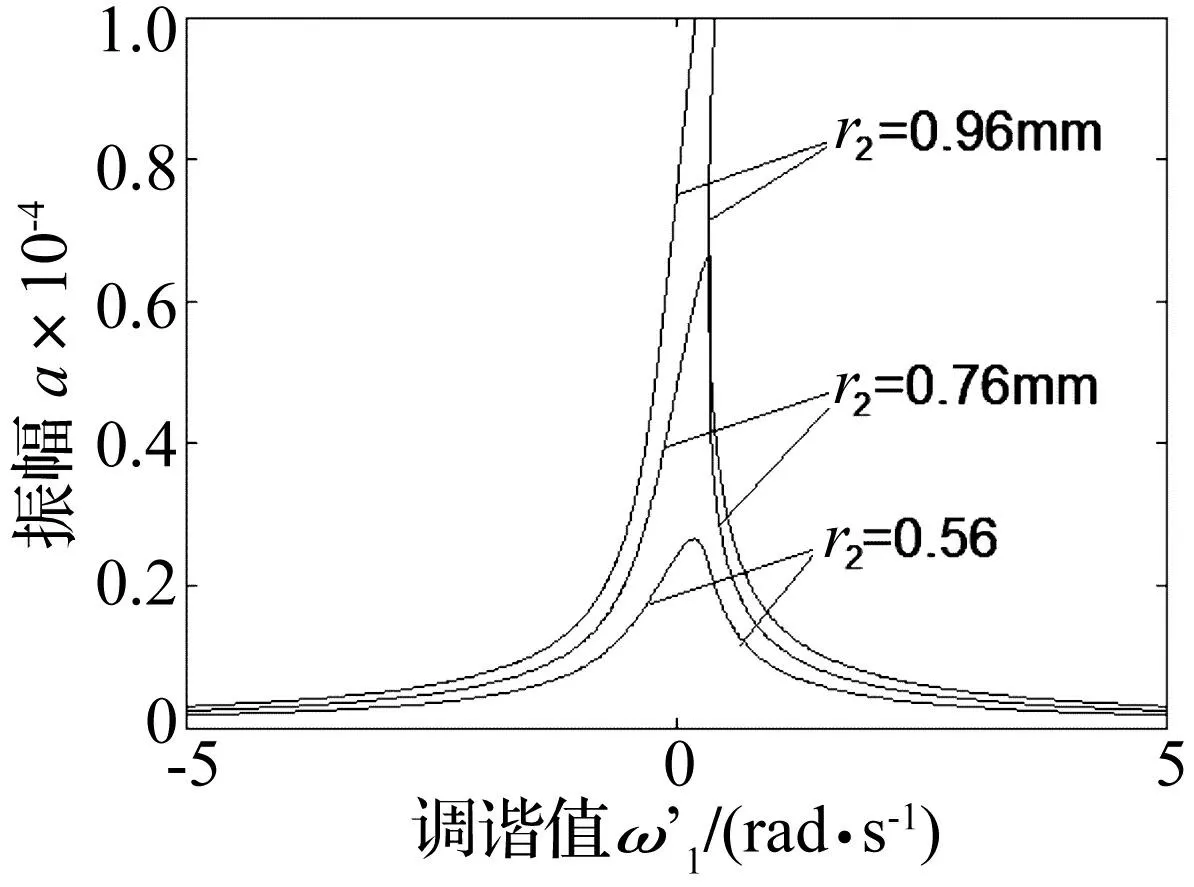
图2　幅频响应曲线 Fig.2 Frequence-response curves

图2是取不同外径r2时的幅频响应曲线，从图中可以振幅和共振区随外径的减小而减小，这是由于减小极板半径极板弯曲刚度增大的缘故。

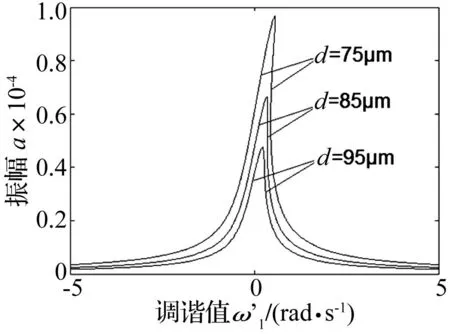
图3　幅频响应曲线 Fig.3 Frequence-response curves

图3为不同的极板间距对应的幅频响应曲线，可以看出极板间距越大振幅和共振区越小。这是因为增大极板间距极板间的电磁力减小的缘故。

图4　幅频响应曲线图 Fig.4 Frequence-response curves

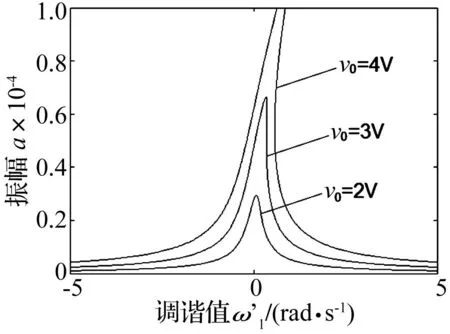
图5　幅频响应曲线图 Fig.5 Frequence-response curves

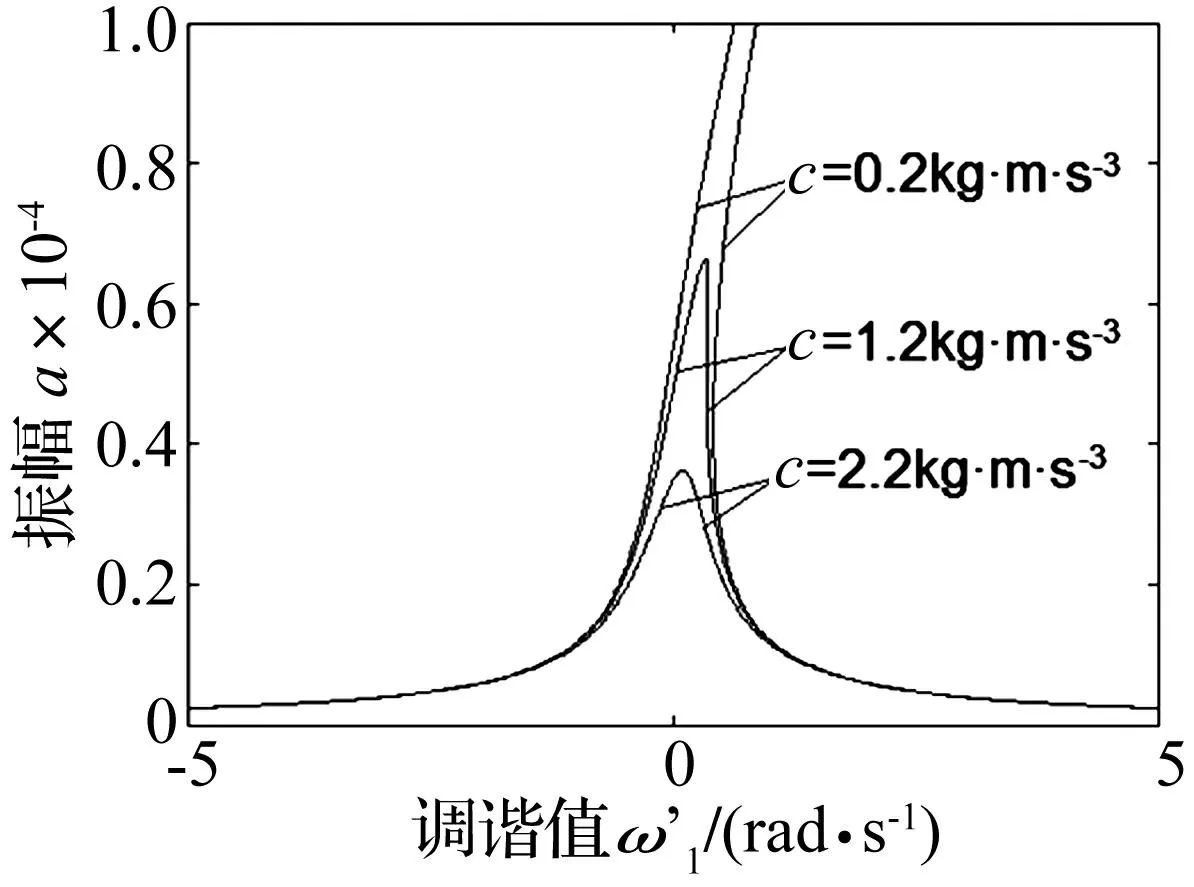
图6　幅频响应曲线 Fig.6 Frequence-response curves

图4是不同的极板厚度对应的幅频响应曲线，可以看出极板厚度越大振幅越小，这是由于这是因为增加极板厚度极板弯曲刚度增大的缘故。但是在图4取值范围内改变极板的厚度对共振区的影响不是太显著。图5是不同的交流电压对应的幅频响应曲线，增大电压幅值振幅和共振区明显的增加，这是由于增大电压的幅值可以使极板间电磁力增大的缘故。图6是不同阻尼系数下的幅频响应曲线，可以看出阻尼越大振幅就越小。

4结论

(1)建立了环形极板机电耦合系统的动力学方程。通过代入参数比较线性项与非线性项的系数可知环形极板机电耦合系统为强非线性系统。

(2)将参数变换思想应用到多尺度法中可以对其进行求解。数值计算结果分析显示：增大交流电压幅值，可以增大振幅和共振区；增大极板间距可以减小振幅和共振区；增大阻尼系数和极板刚度对振幅有抑制作用。

[1]邱家俊. 机电偶联动力系统非线性振动[M]. 北京: 科学出版社, 1996.

[2]Love A. A treatise on the mathematical theory of elasticity[M]. New York： Dover Publications, 1944.

[3]Irie T, Yamada G, Muramoto Y. Natural frequencies of in-plane vibration of annular plates [J]. Journal of Sound and Vibration, 1984, 97(1):171-175.

[4]Ambati G, Bell J F W, Sharp J C K. In-plane vibration of annular rings[J]. Journal of Sound and Vibration, 1976, 47:425-432.

[5]Arafat H N, Neyfeh A H. Combination internal resonances in heated annular plates [J]. Nonlinear Dynamics, 2004,37(4):285-306.

[6]Arafat H N, Neyfeh A H. Modal interations in the vibration of a heated annular plate [J]. International Journal of Nonlinear Mechanics, 2004,39(10):1671-1685.

[7]熊蕊, 刘向东. 含PID控制器的迟滞非线性控制系统的主共振及奇异性[J]. 振动与冲击, 2014, 33(8):72-77.

XIONG Rui, LIU Xiang-dong. Principal resonance and singularity of a hysteretic nonlinear control system with a PID controller [J]. Journal of Vibration and Shock, 2014, 33(8):72-77.

[8]杨志安, 贾尚帅. RLC串联电路与微梁耦合系统的吸合压电与电震荡[J]. 应用力学学报, 2010, 27(4):721-726.

YANG Zhi-an, JIA Shang-shuai. Pull-in voltage and electric oscillations of RLC series circuit and microbeam coupled system [J]. Chinese Journal of Applied Mechanics, 2010, 27(4):721-726.

[9]杨志安, 贾尚帅. RLC串联电路与微梁耦合系统1∶2内共振分析[J]. 应用力学学报, 2010, 27(1):80-85.

YANG Zhi-an, JIA Shang-shuai. Analysis of the 1∶2 internal resonance of coupled RLC circuit and microbeam system [J]. Chinese Journal of Applied Mechanics, 2010, 27(1):80-85.