通过实验模态分析设计阵列式压电模态传感器

通过实验模态分析设计阵列式压电模态传感器

朱峤， 毛崎波

(南昌航空大学飞行器工程学院， 江西南昌330063)

摘要：提出一种新的基于实验模态分析的阵列式压电模态传感器设计方法。首先利用PVDF阵列进行实验模态分析得到结构的曲率模态，然后直接将曲率模态振型函数在相应测量点的幅值作为加权系数，对结构进行模态滤波，得到各阶模态坐标，并加以实验验证。研究发现，利用该方法设计阵列式压电模态传感器是可行的，而且该方法不需要进行复杂的数值计算，操作简单，模态滤波效果良好，可以很容易推广到二维复杂结构，具有较好的工程应用前景。

关键词：模态传感器；PVDF薄膜；实验模态分析；模态滤波；曲率模态

中图分类号:TP212.6

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.19.019

Abstract:By using experimental modal analysis approach, an experimental methodology for design of modal sensors using PVDF array was presented. Firstly, the curvature modal shapes (the second spatial derivatives of modal shapes) of structures were directly obtained with experimental modal analysis using an array of rectangular PVDF patches regularly arranged on the surface of structures. Then, the amplitudes of the curvature modal shape functions at measurement points were taken as weights of PVDF array. The weighted combinations of the PVDF outputs were proportional to responses of target modes. Other modes were filtered out. Numerical simulation and experimental results showed that the proposed method is effective and easy to operate; furthermore, this method can be extended to two-dimensional structures and it has a good prospect of engineering application.

基金项目：高等学校博士点基金(20120023110007);博士研究生拔尖创新人才培育基金(800015Z677) 河北省交通科学基金(Y-20122033)

收稿日期：2014-07-21修改稿收到日期：2014-09-12 2014-06-16修改稿收到日期：2014-08-22

Design of modal sensors using PVDF array based on experimental modal analysis approach

ZHUQiao,MAOQi-bo(School of Aircraft Engineering, Nanchang Hangkong University, Nanchang 330063, China)

Key words:modal sensor; PVDF films; experimental modal analysis; modal filtering; curvature modal shapes

近年来，随着结构振动主动控制技术(Active Structural Vibration Control, ASVC)的发展，利用PVDF薄膜来设计压电模态传感器越来越受到关注[1-5]。模态传感器的核心问题就是把振动结构表面大量的离散振动信息分解为几个高质量的误差信号用于控制器的设计。通过选择其中的若干关键模态(受控模态)分别进行控制，而不影响其它未控的模态，这使得控制器分析设计的难度和工作量大为降低。通过压电模态传感器可以有效防止控制溢出，提高控制系统的稳定性。近年来，也有学者开始把压电模态传感器应用于结构的损伤检测[6-8]。

常用的压电式模态传感器主要有连续分布式和离散阵列式两种，对于连续分布式，主要通过设计压电薄膜的形状函数来实现模态滤波[9-10]。Preumont等[11-12]在指出复杂形状的压电薄膜具有难以加工、误差较大、鲁棒性差等缺点的基础上，提出利用矩形PVDF阵列来测量结构模态坐标，通过设计合理的加权系数，就可以实现对结构的模态滤波。但利用数值方法设计PVDF阵列的加权系数需要大量的计算，测量过程中产生的误差可能会被放大或传播，这就对设计者提出了较高的数学要求。

目前压电模态传感器设计技术的主要困难在于需要预先得到结构的曲率模态(Curvature Mode Shape)。通常是利用传统的加速度计测量得到结构模态振型，然后通过数值计算(如二次中心差分等)得到结构的曲率模态，然而该方法对噪声信号非常敏感。本文模拟固支梁出现程度为10%的双裂纹损伤图1(a)，在模态信号中加入信噪比为90dB的噪声图1(b)，利用二次中心差分分别计算求得加入噪声信号前后结构的曲率模态图1(c)、图1(d)，从图1可以看出，曲率模态指标已经完全失去了对结构损伤检测的敏感性[16]。

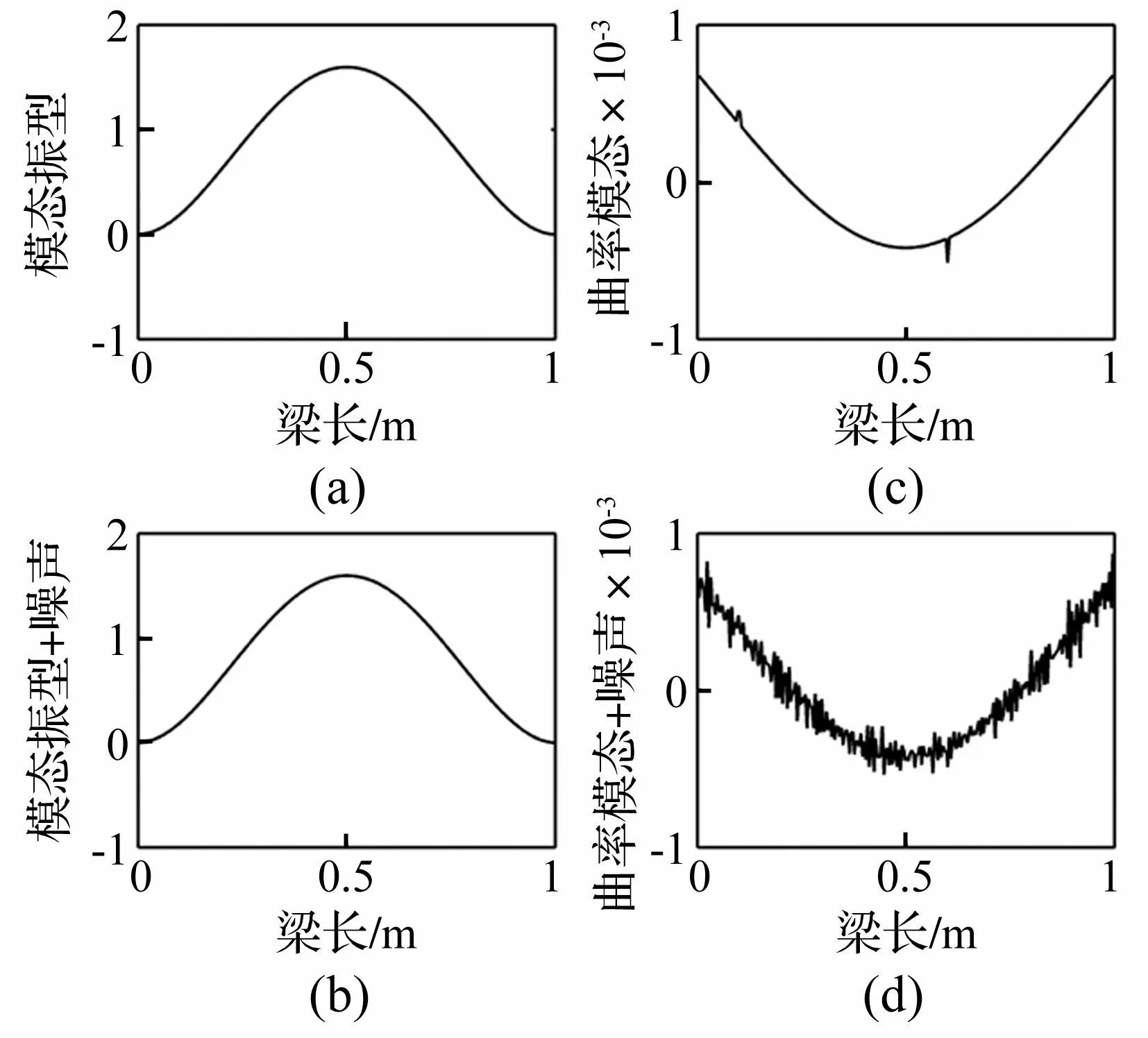
图1　噪声对结构损伤检测的影响 Fig.1 The influence of noise to structural damage detection

为了克服这一缺点，近年来Wang等[13-15]开始对压电模态传感器在结构模态分析中的应用展开研究，并直接利用PVDF阵列测量得到结构的曲率模态。本文即在文献[11-15]的基础上提出一种新的压电模态传感器设计方法。该方法的基本思路为：首先利用PVDF阵列进行实验模态分析得到结构的曲率模态，然后直接将曲率模态振型函数在相应测量点的幅值作为加权系数，对结构进行模态滤波，得到各阶模态坐标。在理论研究和数值计算的基础上，本文分别以两端固支梁和四边固支板为例进行实验验证。

1基本理论

1.1阵列式压电模态传感器原理

阵列式压电模态传感器的工作原理见图2，即通过设计合理加权系数，使各块PVDF输出的线性加权和正比于结构的第k阶模态坐标：

(1)

式中，Wnk为第n块PVDF对应第k阶模态的加权系数。

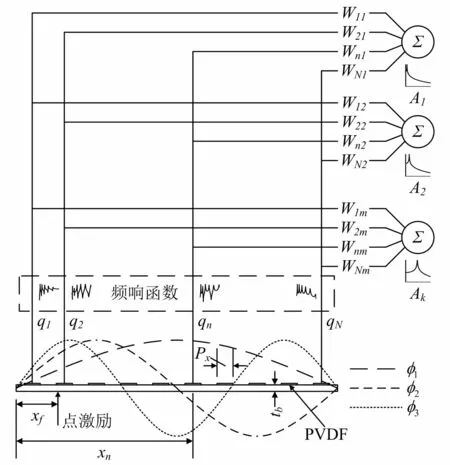
图2　阵列式压电模态传感器原理 Fig.2 Theory of the piezoelectric modal sensor array

假设图2中的弹性梁长为Lx，宽为Ly，在其表面均匀布置N片形状相同的矩形PVDF压电薄膜，由文献[10]可知，第n片PVDF的输出电荷qn可以表示为：

(2)

式中，e31为压电常数，Px、Py、tp分别为PVDF的长度、宽度和厚度，tb为梁的厚度，xn为第n块PVDF的中心位置，y(x)表示梁的法向位移，由模态理论可知：

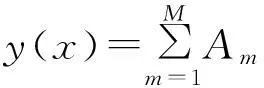
(3)

式中，Am为第m阶结构模态坐标，φm(x)为梁的第m阶结构模态(振型函数)，M表示所取最大结构模态阶数。

将式(2)和式(3)代入式(1)可得：

(4)

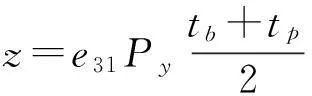
由微分中值定理可知，式(4)可以表示为：

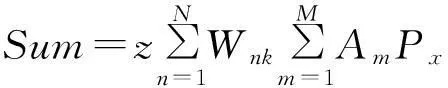
(5)

式中，xn-Px/2≤xn≤xn+Px/2。

对于经典边界条件，结构曲率模态的正交性可以表示为：

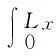
(6)

由文献[12-14]可知，可以对式(6)中结构曲率模态进行离散化，得到的离散曲率模态同样具有类似的正交性，即：

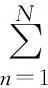
(7)

式中，c为常数。

由式(7)可知，如果令

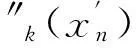
(8)

将式(8)代入式(5)则有

Sum=zPxAk∝Ak

(9)

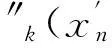
1.2利用PVDF阵列进行实验模态分析

注意到式(8)中结构曲率模态的获取一般都是基于对结构模态振型的数值计算(如二次中心差分等)[18]，该方法对噪声信号非常敏感。本文利用文献[15]提出的实验模态分析方法直接测量得到结构的曲率模态。

见图2，假设在弹性梁表面xf位置施加点激励f(x,t)，可以表示为：

f(x)=Fδ(x-xf)

(10)

式中，F表示激励力幅值，δ(x)为单位脉冲函数。

由文献[17]可知，梁结构第m阶模态坐标Am可以表示为：

(11)

式中，ρb为梁的密度，ωm、ξm分别为和第m阶固有频率和阻尼比，ω为激励力频率。

结合式(2)、式(3)和式(11)，并由中值定理可知，阵列式压电模态传感器中第n块PVDF输出电压和点激励幅值之间的频率响应函数(Frequency Response Function)可以表示为：

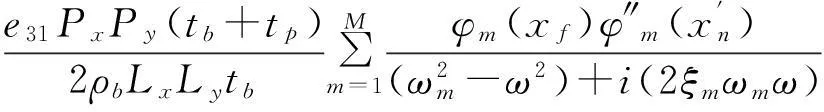
(12)

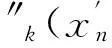
2数值分析

为了验证利用实验模态分析设计阵列式压电模态传感器的可行性，本文以固支梁为例进行数值计算分析。设梁的长度Lx=905mm，宽度Ly=50mm，厚度tb=5mm，弹性模量E=70GN/m2，密度ρ=2700kg/m3，阻尼比ζ=0.01。见图3，首先沿长度方向将固支梁均匀划分为10个测量单元，把30×12mm2的矩形PVDF压电薄膜粘贴在每个单元中心位置，点激励作用于2号单元中心位置。

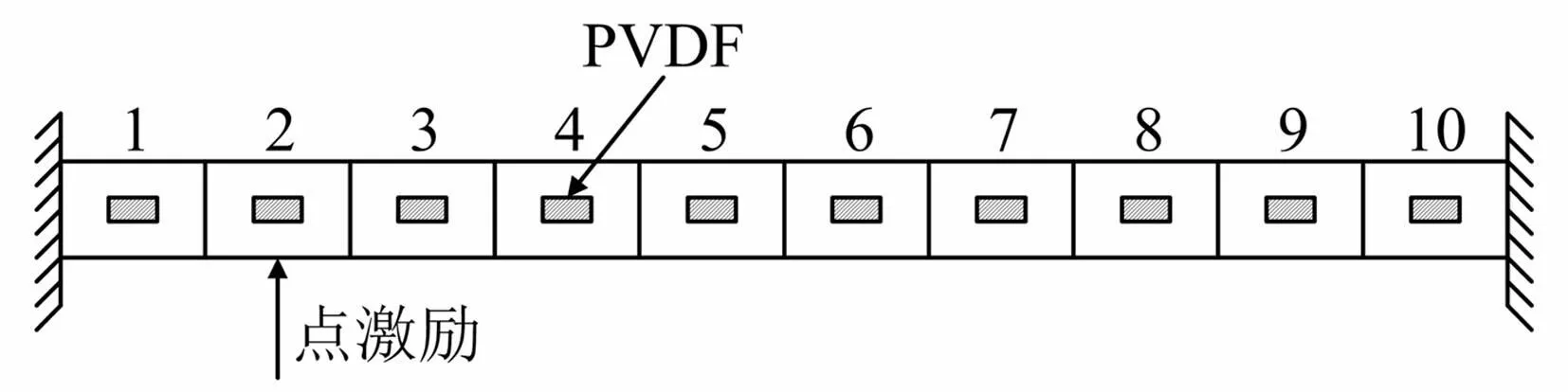
图3　PVDF阵列示意图 Fig.3 PVDF array

图4给出了利用PVDF阵列进行模态分析得到的固支梁的前4阶曲率模态。从图中可以看出，由实验模态分析得到的结果与理论值非常吻合。

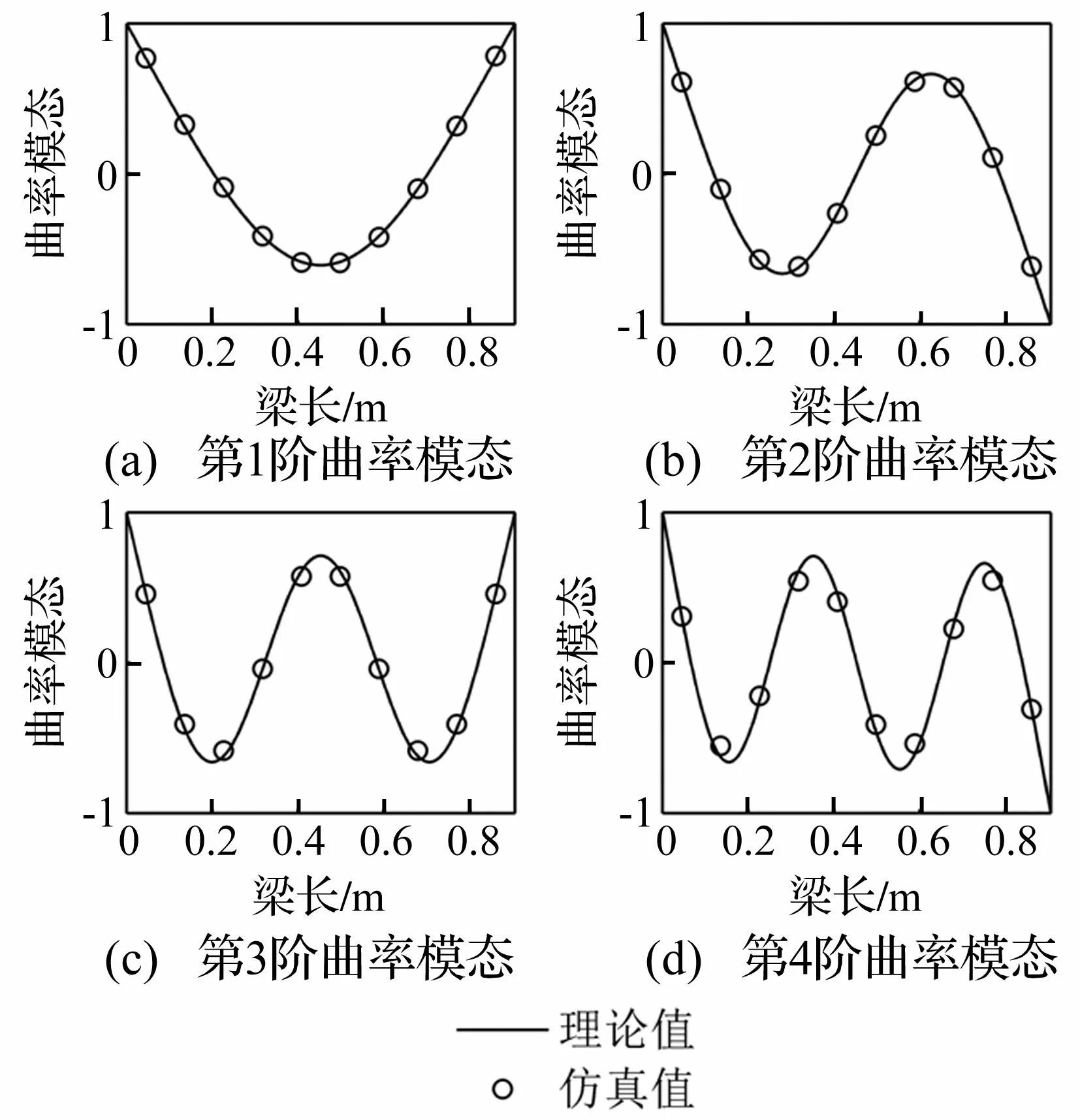
图4　固支梁前4阶曲率模态 Fig.4 The first four curvature mode shapes of the clamped beam

结合式(8)和式(9)，直接将实验模态分析的结果作为加权系数，对固支梁进行模态滤波，结果见图5。从图中可以看出，各目标阶固有频率处峰值远大于其他峰值，模态滤波效果良好，这说明利用本文方法设计阵列式压电模态传感器是可行的。

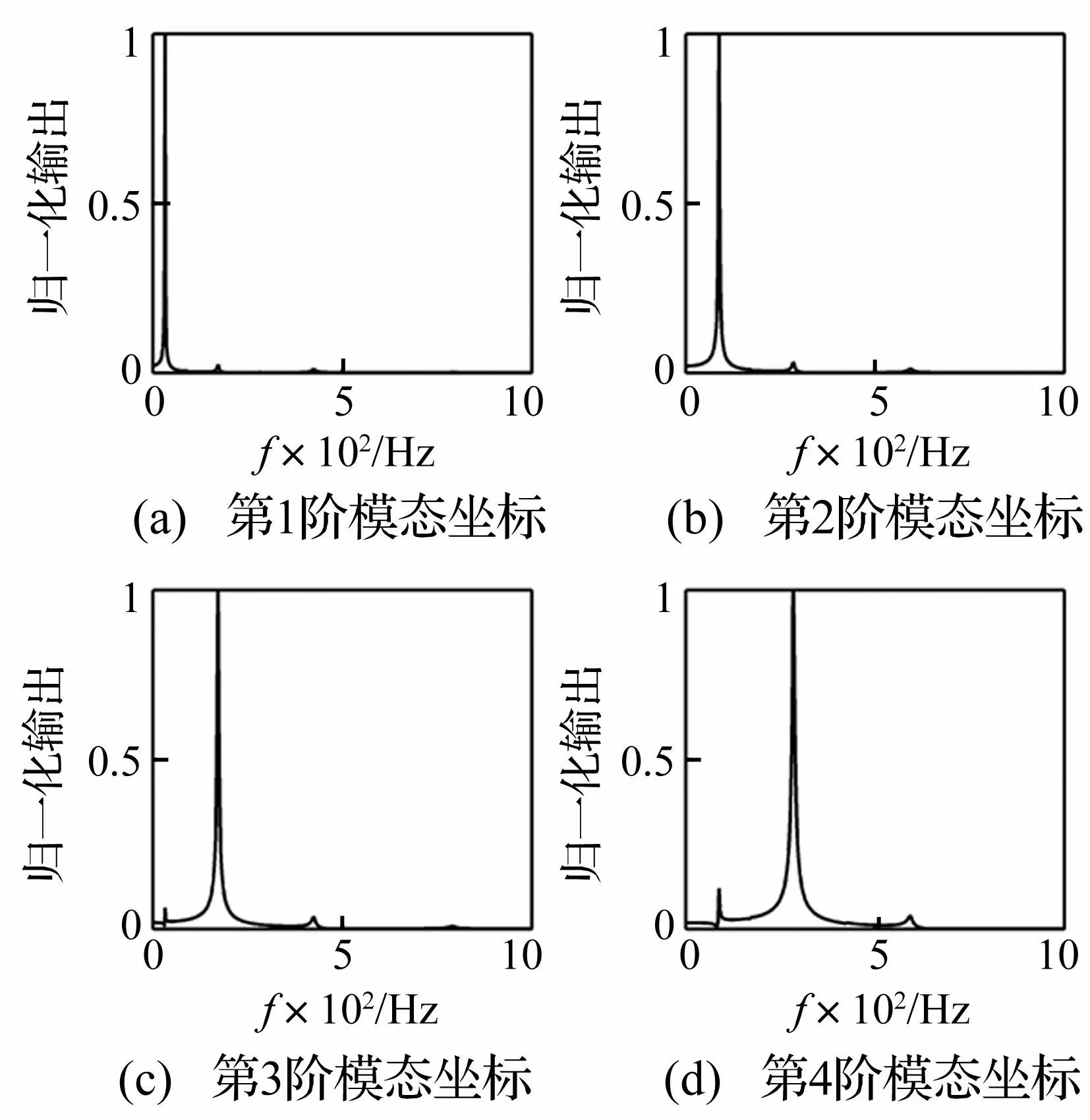
图5　固支梁前4阶模态滤波结果(10片PVDF) Fig.5 The first four modal filtering results of the clamped beam (with 10 PVDF patches)

注意到图5中非目标阶固有频率处仍有极小峰值出现，这主要是由于梁上划分的测量单元数有限。图6给出了将固支梁均匀划分为20个测量单元后前4阶模态滤波结果。对比图5和图6可以发现，模态传感器的滤波效果明显提高，这说明随着PVDF数目的增加，利用本文方法设计的阵列式压电模态传感器将具有更好的模态滤波效果。

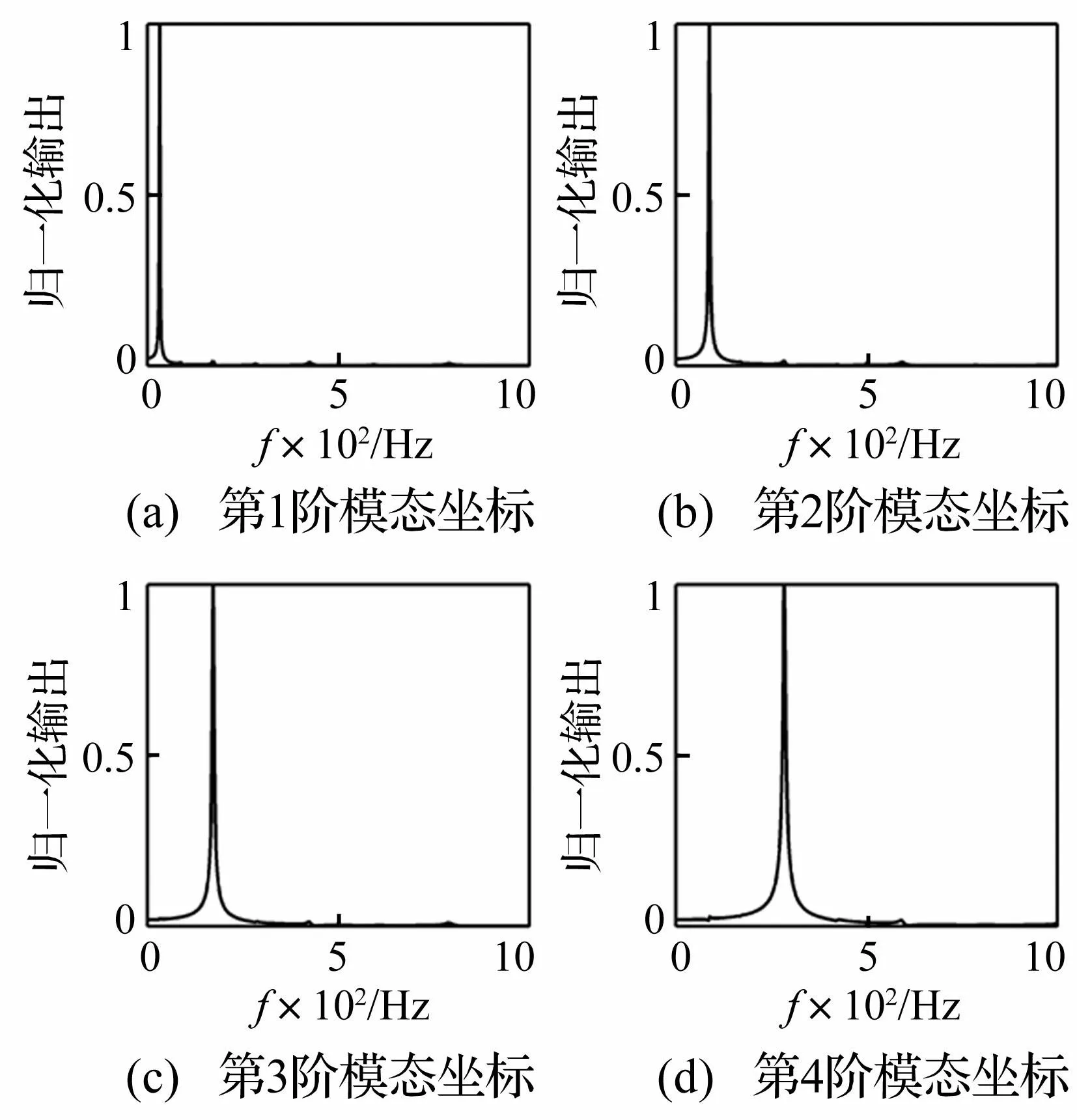
图6　固支梁前4阶模态滤波结果(20片PVDF) Fig.6 The first four modal filtering results of the clamped beam (with 20 PVDF patches)

3实验研究

为了进一步验证本文方法的有效性，首先取两端固支铝梁进行实验研究，所用梁的物理参数与数值分析一致。沿实验梁长度方向将10片PVDF压电薄膜均匀粘贴在梁表面，该梁两端通过螺栓进行固定，见图7。实验过程中使用的PVDF压电薄膜的物理参数见表1。

图7　实验梁PVDF阵列 Fig.7 PVDF array on the experimental beam

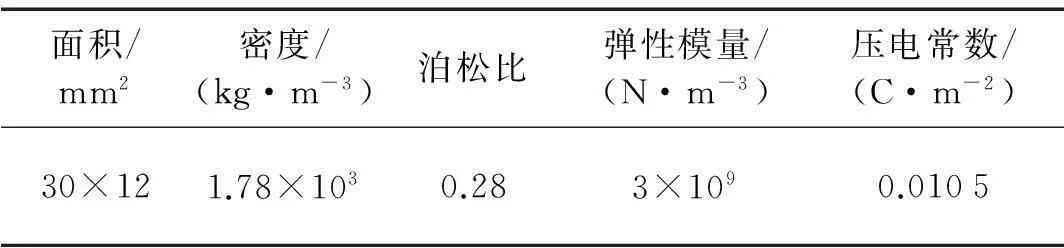
面积/mm2密度/(kg·m-3)泊松比弹性模量/(N·m-3)压电常数/(C·m-2)30×121.78×1030.283×1090.0105

首先使用冲击力锤在2号单元中心位置施加点激励，利用CL-YD-303力传感器测量激励力，并通过江苏联能公司的YE6251力学实验系统采集各块PVDF压电薄膜的输出电荷和力传感器测得的力信号从而得到一组频率响应函数。然后利用南京航空航天大学的N-Modal模态分析软件对实验梁进行模态分析，结果见图8。

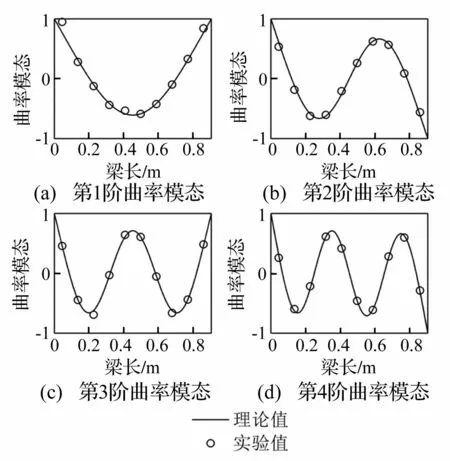
图8　实验梁前4阶曲率模态 Fig.8 The first four curvature mode shapes of the experimental beam

表2和表3分别给出了实验梁前4阶固有频率和实验模态分析得前4阶曲率模态的模态置信矩阵(Modal Assurance Criterion，MAC)。

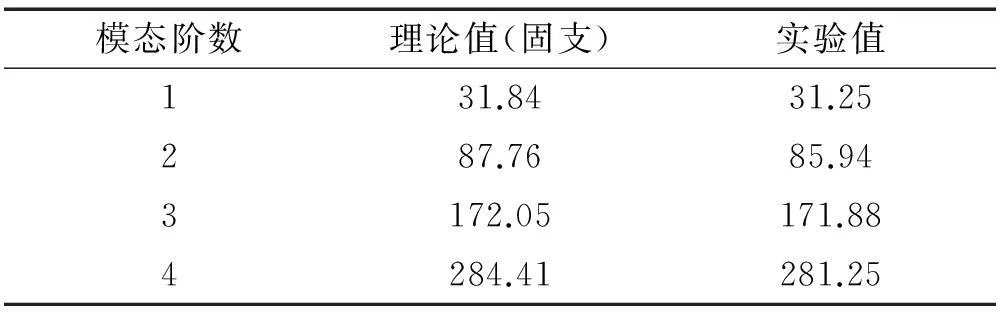
表2　实验梁前4阶固有频率(Hz)

表3　实验梁前4阶曲率模态MAC

根据式(8)和式(9)，直接将实验模态分析得到的结果作为加权系数，对实验梁进行模态滤波，结果见图9。对比图5和图9可以发现，实验模态滤波结果中非目标阶模态坐标并没有完全消除，这主要是由于实验过程中梁的边界条件与理想固支边界条件有一定误差，从表2中可以看出，实验梁前4阶固有频率与理论值之间有2%左右的误差。同时PVDF压电薄膜由于人工粘贴导致的位置偏差和测量过程中的环境噪声也会对模态滤波结果带来一定的干扰。

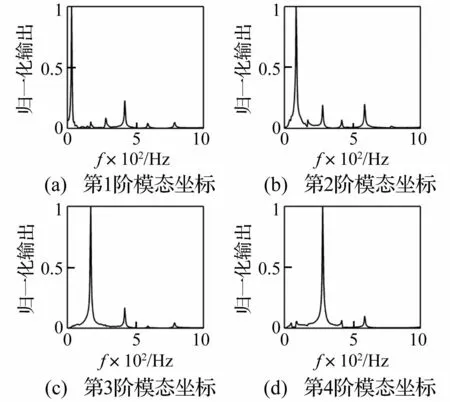
图9　实验梁前4阶滤波实验结果 Fig.9 The first four modal filtering results of the experimental beam

但注意到表3中MAC矩阵的非对角元素非常接近于0，这表明利用PVDF阵列对实验梁进行模态分析得到的前4阶曲率模态具有较好的正交性。图10给出了第2阶模态滤波结果和PVDF阵列中第2片输出以及PVDF阵列输出平均值的比较。注意到图9中目标阶固有频率处峰值远大于其他阶，同时比较图10中的模态滤波结果与滤波之前的PVDF输出可以发现，非目标阶固有频率处峰值大为降低，这表明所设计模态传感器具有较好的滤波效果。

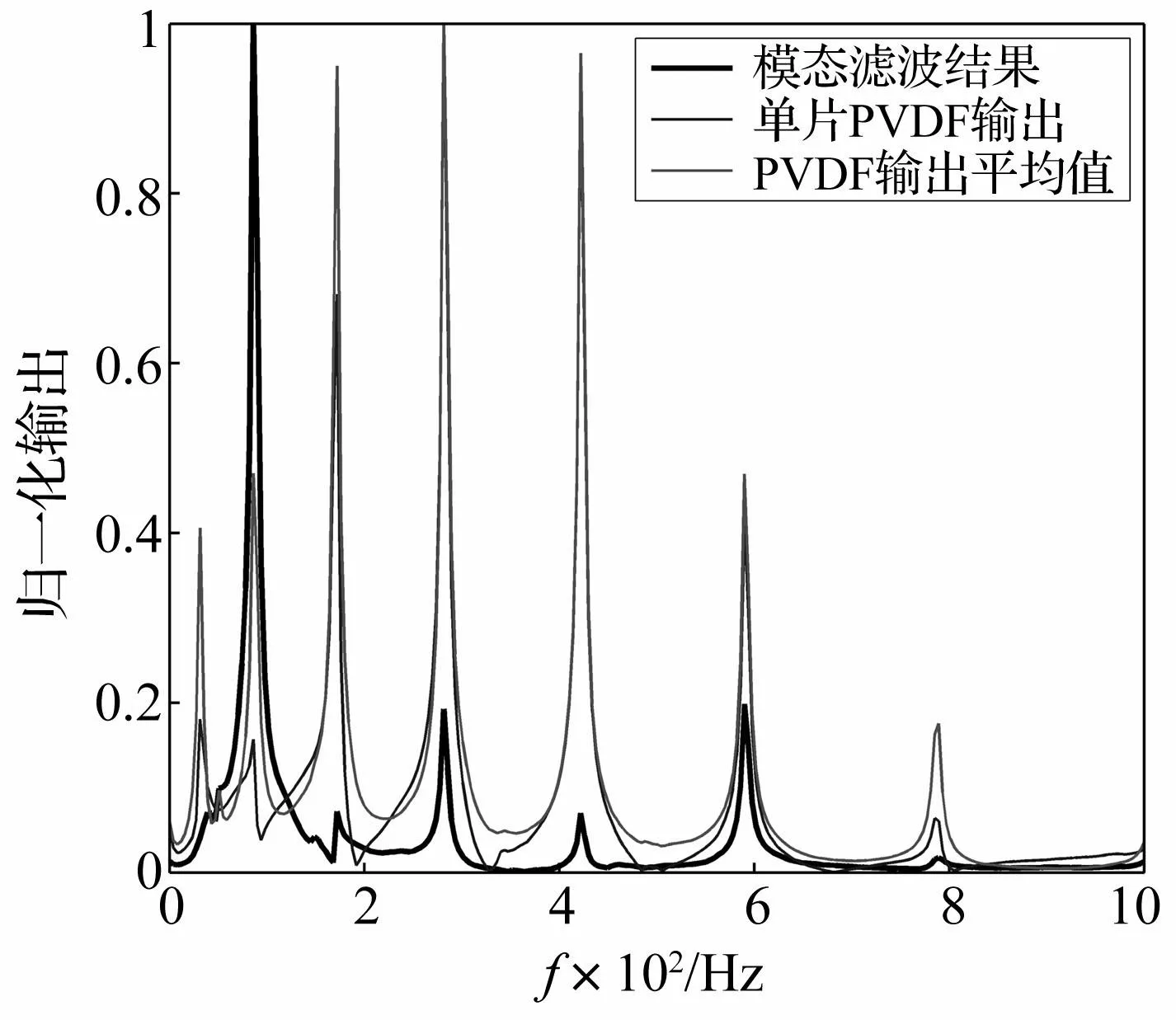
图10　模态滤波结果和PVDF输出对比 Fig.10 The contrast of modal filtering results and outputs of PVDF

利用本文方法设计阵列式压电模态传感器不仅有效避免了测量误差在大量复杂运算过程中的放大和传播[2,18]，而且与文献[18]相比可以看出，在具有不逊于其模态滤波效果的基础上，本文方法操作简单，更易于在工程实际中应用。

注意到本文阵列式压电模态传感器的设计原理可以很容易推广到二维结构，我们进一步取四边固支铝板进行实验研究。首先把实验板均匀划分为7×7的测量单元网格，将49片PVDF压电薄膜均匀粘贴在板表面，使用冲击力锤在33号单元中心位置施加点激励，见图11。实验板四边均用相同材质的一组铝梁上下夹紧，并通过螺栓固定在由角钢搭成的台架上，见图12。

图11　实验板PVDF阵列示意图 Fig.11 Diagram of PVDF array on the experimental plate

图12　实验板上PVDF阵列 Fig.12 PVDF array on the experimental plate

图13和图14分别给出了利用本文方法得到的实验板前3阶曲率模态和模态滤波结果。从图14中可以看出，非目标阶固有频率处峰值远小于目标阶，模态滤波效果良好。这不仅进一步验证了利用实验模态分析对结构进行模态滤波是有效可行的，同时也表明本文方法可以很容易推广到二维复杂结构，具有良好的实际工程应用前景。

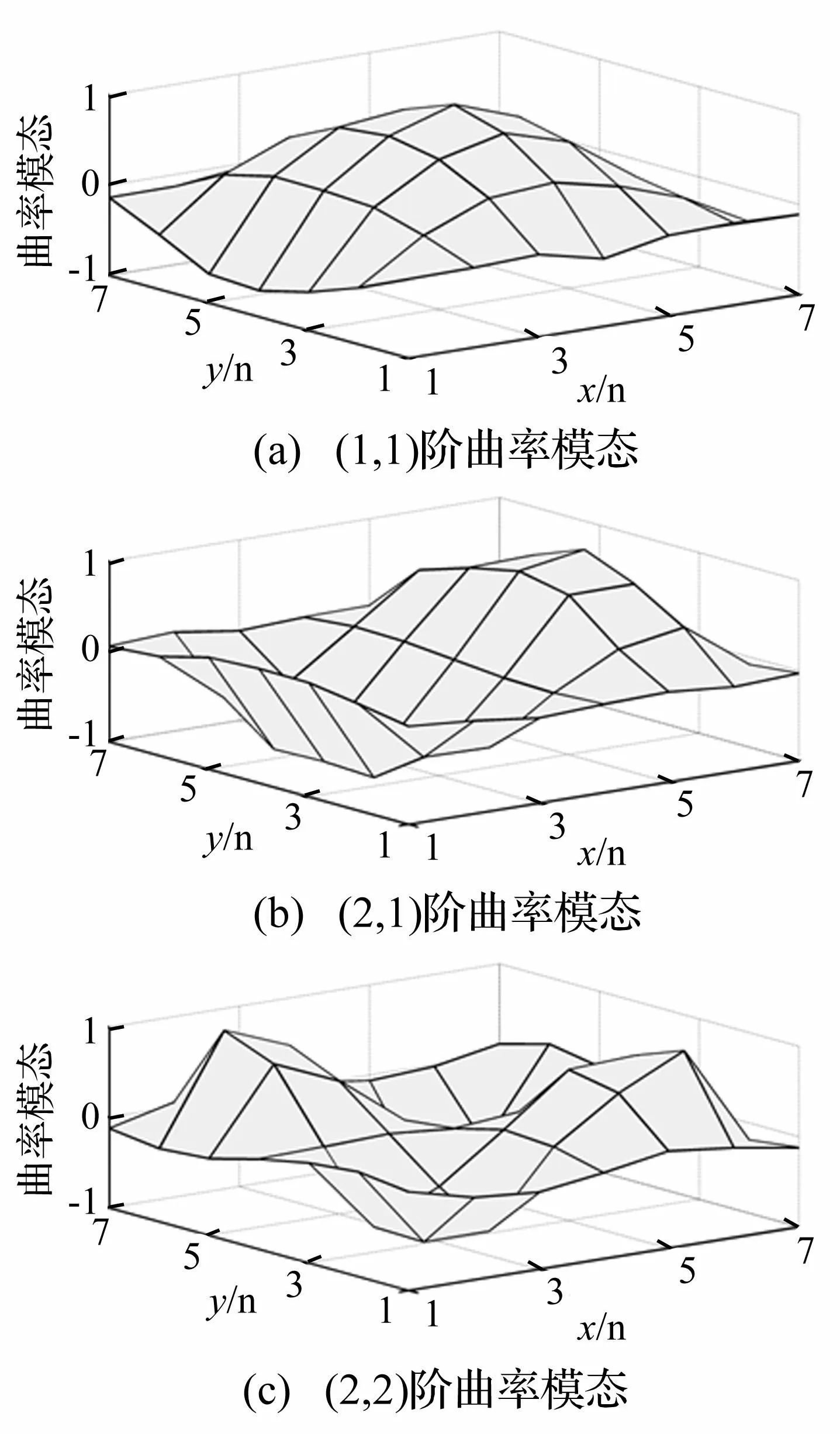
图13　实验板前3阶曲率模态 Fig.13 The first three curvature mode shape of plate

图14　固支板前3阶滤波实验结果 Fig.14 The first three modal filtering results of plate

4结论

本文提出了一种新的基于实验模态分析的阵列式压电模态传感器设计方法，在理论研究和数值计算的基础上，本文分别以两端固支梁和四边固支板为例进行实验验证。研究发现，利用本文方法设计阵列式压电模态传感器是可行的。与传统的模态传感器设计方法(如文献[19])相比，本文方法不仅操作简单，不需要大量复杂的数据运算，而且模态滤波效果更加良好，可以很容易推广到二维复杂结构，具有良好的实际工程应用前景。

参考文献

[1]Preumont A, François A, De Man P, et al. Distributed sensors with piezoelectric films in design of spatial filters for structural control[J]. Journal of Sound and Vibration, 2005, 282(3): 701-712.

[2]Preumont A, François A, De Man P, et al. Spatial filters in structural control[J]. Journal of Sound and Vibration, 2003, 265(1): 61-79.

[3]Gardonio P, Lee Y S, Elliott S J, et al. Analysis and measurement of a matched volume velocity sensor and uniform force actuator for active structural acoustic control[J]. The Journal of the Acoustical Society ofAmerica, 2001, 110(6): 3025-3031.

[4]Pietrzko S J, Mao Q. New results in active and passive control of sound transmission through double wall structures[J]. Aerospace Science and Technology, 2008, 12(1): 42-53.

[5]范志强，马宏昊，沈兆武，等. 夹心式PVDF压力传感器压电特性及标定装置研究[J]. 振动与冲击, 2014, 33(16): 68-71.

FAN Zhi-qiang, MA Hong-hao, SHEN Zhao-wu, et al. Piezoelectric property of sandwich PVDF pressure gauge and its calibration device[J]. Journal of Vibration and Shock, 2014, 33(16): 68-71.

[6]Qiao Pi-zhong, Lu Kan, Lestari W, et al. Curvature mode shape-based damage detection in composite laminated plates[J]. Composite Structures, 2007, 80(3): 409-428.

[7]Hamey C S, Lestari W, Qiao P, et al. Experimental damage identification of carbon/epoxy composite beams using curvature mode shapes[J]. Structural Health Monitoring, 2004, 3(4): 333-353.

[8]Dixit A, Hanagud S. Comments on: Curvature mode shape-based damage assessment of carbon/epoxy compositebeams[J]. Journal of Intelligent Material Systems and Structures, 2010, 21(6): 659-663.

[9]Lee C K, Moon F C. Modal sensors/actuators[J]. ASME Transactions Series E Journal of Applied Mechanics, 1990, 57: 434-441.

[10]Gu Y, Clark R L, Fuller C R, et al. Experiments on active control of plate vibration using piezoelectric actuators and polyvinylidene fluoride (PVDF) modal sensors[J]. Journal of Vibration and Acoustics, 1994, 116(3): 303-308.

[11]Preumont A, Francois A, Dubru S. Piezoelectric array sensing for real-time, broad-band sound radiation measurement[J]. Journal of Vibration and Acoustics, 1999, 121(4): 446-452.

[12]Mao Qi-bo, Pietrzko S J. Measurements of local volume displacement using a piezoelectric array[J]. Acta Acustica United with Acustica, 2006, 92(4): 556-566.

[13]Wang B T, Rogers C A. Modeling of finite-length spatially-distributed induced strain actuators for laminate beams and plates[J]. Journal of Intelligent Material Systems and Structures, 1991, 2(1): 38-58.

[14]Wang B T, Wang C C. Feasibility analysis of using Piezoceramic transducers for cantilever beam modal testing[J].Smart Materials and Structures, 1997, 6: 106-116.

[15]Chen R L,Wang B T. The use of polyvinylidene fluoride films as sensors for the experimental modal analysis of structures[J]. Smart Materials and Structures, 2004, 13: 791-799.

[16]Yoon M K, Heider D, Gillespie Jr J W, et al. Local damage detection with the global fitting method using operating deflection shape data[J]. Journal of Nondestructive Evaluation, 2010, 29(1): 25-37.

[17]Wang B T. Structural modal testing with various actuators and sensors[J]. Mechanical Systems and Signal Processing, 1998, 12(5): 627-639.

[18]Carden E P, Fanning P. Vibration based condition monitoring: a review[J]. Structural Health Monitoring, 2004, 3(4): 355-377.

[19]Sumali H, Meissner K, Cudney H H. A piezoelectric array for sensing vibration modal coordinates[J]. Sensors and Actuators A: Physical, 2001, 93(2): 123-131.

第一作者王建国男，博士，讲师,1987年生

第一作者张献民男，教授，1959年生