曼型干式煤气柜动力特性分析及风振响应主要贡献模态识别

曼型干式煤气柜动力特性分析及风振响应主要贡献模态识别

李正良1，2， 刘欣鹏1， 晏致涛1，2， 焦红伟1， 俞登科1

(1.重庆大学土木工程学院，重庆400045；2.重庆大学山地城镇建设与新技术教育部重点实验室，重庆400045)

摘要：曼型干式煤气柜不同于一般空间结构，其动力特性十分复杂，作为研究其频域内风振响应的基础，首先通过建立精细化有限元模型研究其在不同工况下的动力特性；其次，分别计算背景、共振响应振型能量参与系数，并按降序排列，选取结构风振响应的主要模态;最后，通过选取模态进行频域计算并与传统频域计算方法(完全二次振型叠加，CQC法)对比。结果表明：结构自振频率分布密集；动力特性受活塞位置及内部气压影响较大；背景、共振响应振型能量参与系数能准确反映各阶模态能量对响应总能量的贡献程度；通过振型能量参与系数法确定的主要模态进行频域分析具有计算效率高，计算精度可控的优点。

关键词：动力特性；背景响应；共振响应；脉动风荷载；振型能量参与系数；频域分析

中图分类号:TU973+.213；TU33+3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.19.012

Abstract:The dynamic characteristics of a MAN type dry gas storage tank are very complex, they are different from those of ordinary spatial structures. Here, as the basis of its wind-induced response analysis in frequency domain, its dynamic characteristics were analyzed under different working conditions by using the finite element method. Its modes were sorted with order-descending according to the calculation results of mode energy participation factors of background response and resonant response, respectively. Then, the modes with significant contributions to its wind-induced vibration were selected. Finally, the results calculated in frequency domain with a selected modes were compared with those calculated with CQC method. The results showed that the modal frequency distribution of the structure is dense; the location of piston and internal pressure have larger influences on the dynamic characteristics of the gas storage tank; the mode energy participation factors of background response and resonant one can reflect the contributions of different order modes’ energy to the total energy of the response; the analysis in frequency domain with the main modes determined using the mode energy participation factors has advantages of higher calculation efficiency and controllable computation accuracy.

基金项目：国家自然科学基金(61004067)资助项目

收稿日期：2014-08-01修改稿收到日期：2014-09-18

Dynamic characteristics of a MAN type dry gas storage tank and recognition of main modes with contributions to its wind-induced vibration

LIZheng-liang1,2,LIUXin-peng1,YANZhi-tao1,2,JIAOHong-wei1,YUDeng-ke1(1. School of Civil Engineering, Chongqing University, Chongqing 400045, China；2. Key Laboratory of New Technology for Construction of Cities in Mountain Area,Ministry of Education, Chongqing University, Chongqing 400045, China)

Key words:dynamic characteristics; background response; resonant response; fluctuating wind loads; mode energy participation factor; analysis in frequency domain

曼型干式煤气柜(下文简称新型煤气柜)是一种储存可燃气体的大型重要建筑物，广泛用于冶金、石化和市政等行业，其在节约能源和保护环境上发挥着重大作用。近年来，随着我国钢铁行业的发展，国内开始大量建造该类煤气柜。

新型煤气柜作为空间结构的代表，与传统高层建筑结构多侧重抗震性能的研究不同[1]，其风振响应已成为控制结构设计的关键因素之一。因此对此类结构风振响应分析成为了亟待解决的重要问题。从目前的研究状况来看，在模态分解法的基础上，利用随机振动理论来求解结构在脉动风作用下的动力风致响应即频域法，是分析空间结构的首选方法。

然而，与一般高层建筑结构形式不同，新型煤气柜具有高跨比较小；柜壁较薄，易产生局部振动；内部活塞质量巨大，对煤气柜动力特性影响显著等特点。国内对于此类新型结构形式的动力特性分析尚属空白。因此作为频域分析法的基础，对其动力特性的精细化分析尤为重要。

另外，在频域内计算大跨度空间结构的脉动风振响应一般采用两种方法：基于荷载空间分布模式的Ritz向量叠加法[2]和完全二次振型叠加法(CQC)[3-4]。Ritz向量叠加法基本特点是在确定结构主要模态时，考虑了外荷载的空间分布模式对激发结构模态特性的影响，过滤掉与荷载分布向量正交的振型，从而在进行频域计算是大大减少了计算量，提高了计算效率，然而对于时空分布较复杂的脉动风荷载来说，确定荷载分布模式较为困难，限制了Ritz向量叠加法在风振响应分析中的应用。对于传统的频域计算方法，即完全二次振型叠加法，该方法自动包含了所有主要模态的耦合项，计算精度较高。工程分析中，往往取前10～20阶模态进行计算，但这种做法，对于大型空间结构来说，往往会忽略某些对风振响应贡献较大的高阶模态[5-10]，因此如何合理考虑高阶振型对结构风振响应的影响是采用频域分析法计算结构风振响应的重要问题。对于曼型煤气柜这种新型结构形式，国内对其动力特性及主要贡献模态的研究尚属空白。本文总结了振型叠加法计算结构风振响应的公式[11]，以及背景响应与共振响应的计算方法[12-14]，并将背景—共振响应振型能量参与系数法引入该类复杂空间结构中，从能量的角度定量的选取风振响应中的主要贡献模态，解决了该类结构风振响应计算精度的评价问题。

1煤气柜动力特性分析

1.1煤气柜简介

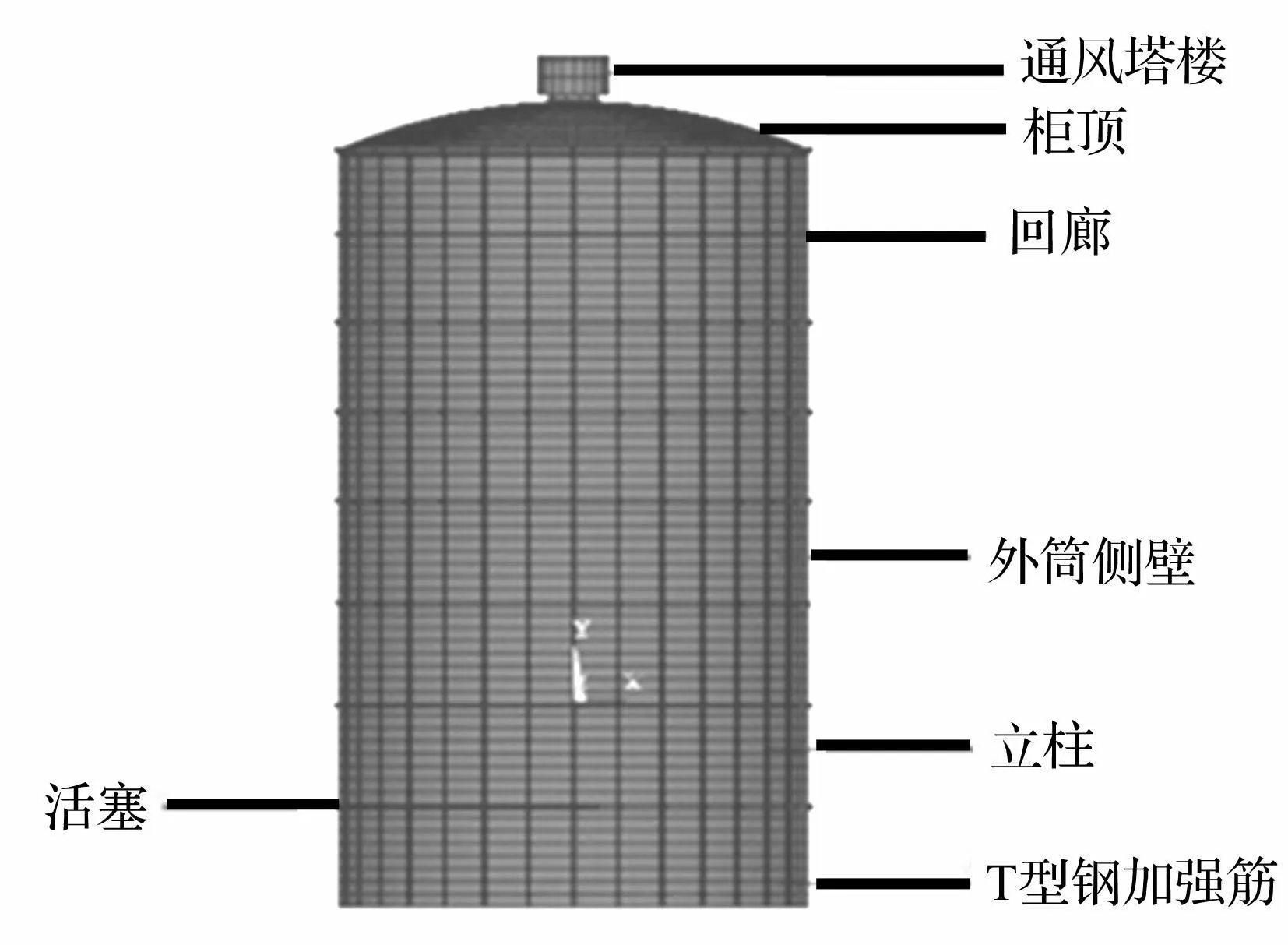
图1　新型煤气柜几何模型图 Fig.1 The geometry model of new type dry gas tank

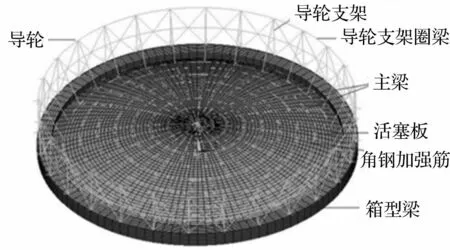
图2　活塞几何模型图 Fig.2 The geometry model of new type dry gas tank piston

曼型干式煤气柜由外筒、柜顶、内部活塞以及附属结构(通风塔楼、外部电梯、外部楼梯等)组成，本文研究的煤气柜的储气规模为30万m3，其中该类煤气柜的主要外形尺寸为：煤气柜总高120m，柜体侧壁高108m，外筒半径66m，活塞总行程96m，柜顶与活塞的拱顶曲率半径为88m，所有型钢及钢板为Q235钢，见图1～图2。

1.2无内压作用煤气柜模态分析

不考虑柜体内外气体压力差，利用ANSYS有限元分析软件分别对煤气柜在三种工况(活塞高位、中位、低位)下的动力特性进行分析。由于煤气柜是轴对称结构，因此在模态分析时均将振动形式相同的模态合并。

1.2.1柜体在活塞高位状态下的模态和频率

煤气柜在活塞位于高位时(活塞底部距离地面97.2m)，通过模态分析得到结构的频率和模态如表1和图3(由于篇幅限制仅给出典型模态，下同)。

表1　 新型煤气柜结构的自振频率

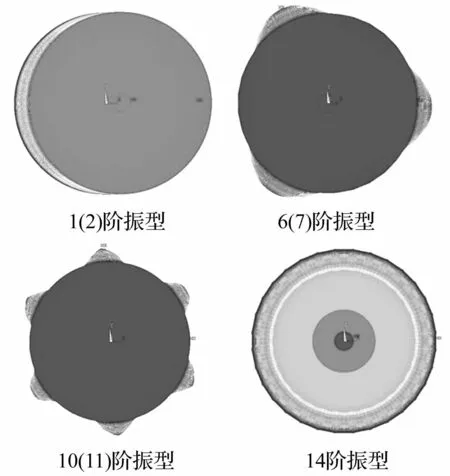
图3　煤气柜振型图 Fig.3 Vibration chart of new type gas tank

分析可知：当活塞位于高位时，其自振频率的分布比较密集，前40阶模态频率分布在1.3～7Hz；柜顶的振动模态仅出现在第14和25阶，这一定程度说明柜顶的刚度要明显大于柜体；结构前25阶振型中，一、二阶振型为x,y方向的悬臂梁式振动，第三阶振型为结构的扭转振动，其余各阶均为壳体的局部振动。

1.2.2柜体在活塞中位状态下的模态和频率

煤气柜在活塞位于中位时(活塞底部距离地面54m)，通过模态分析得到结构的频率和振型如表2和图4。

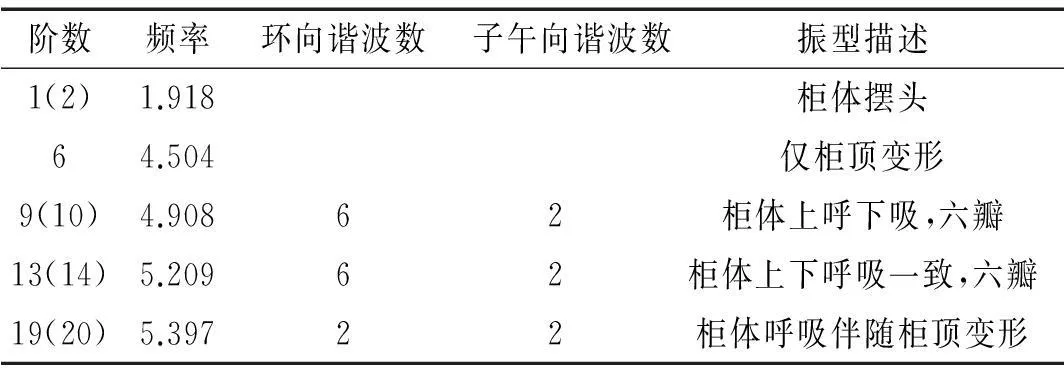
表2　新型煤气柜结构的自振频率

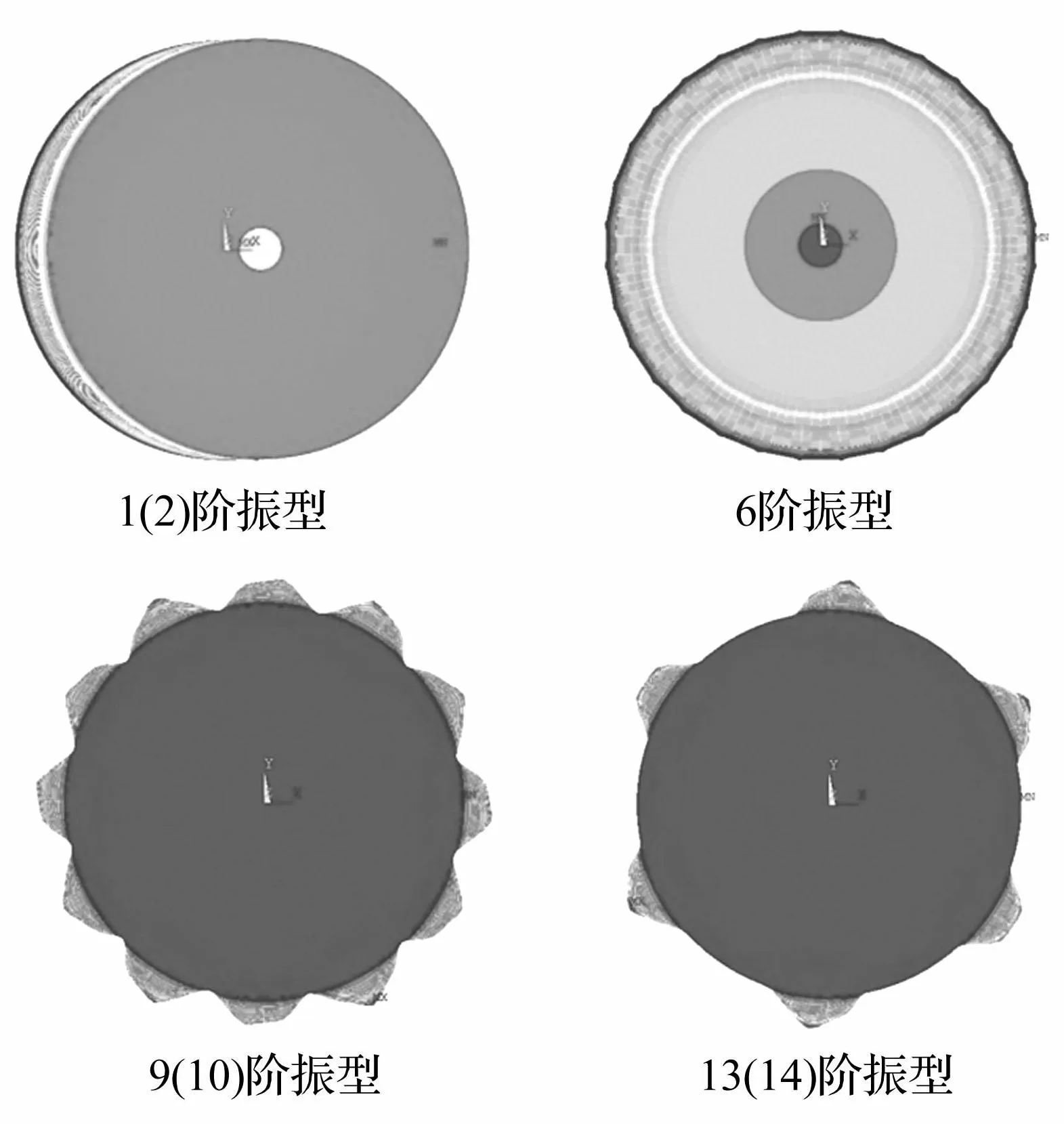
图4　煤气柜振型图 Fig.4 Vibration chart of new type gas tank

分析可知：当活塞位于中位时，煤气柜模态频率比高位模态频率大，柜体整体刚度增大；与高位时模态一样，自振频率的分布比较密集，前40阶振型的频率分布在2～7Hz；结构前25阶振型中，一、二阶振型为x,y方向的悬臂梁式振动，第三阶振型为结构的扭转振动，这与活塞高位时的振动形态相似，但其对应的自振频率与活塞高位差别较大。对于高阶模态，尽管两种工况下(活塞高、中位)均为壳体的局部振动，但相应阶数的模态振动形式及其对应自振频率均变化较大，这是因为活塞的位置变化对结构的动力特性影响很大。

1.2.3柜体在活塞低位状态下的模态和频率

煤气柜在活塞低位状态下(活塞底部距离地面3.6m)，通过模态分析得到结构的频率和振型如表3和图5。

表3　新型煤气柜结构的自振频率

图5　煤气柜振型图 Fig.5 Vibration chart of new type gas tank

分析可知：结构模态频率比前两种工况相应模态频率大；前40阶振型的频率分布在2.7～7Hz，自振频率的分布相对高位和中位更密集；随着活塞位置的继续下降，煤气柜前25阶振型中，不同于高位和中位振型，低位的一阶振型为环向四个波形的壳体振动，第二、三阶振型为悬臂梁式振动，柜体的扭转振动出现在第18阶，其余为壳体的局部模态。

1.3内压作用下煤气柜结构模态分析

煤气柜处于工作状态时，内部封闭有一定压力的煤气，30万m3的煤气柜设计内压为15kPa。内压的存在将会影响结构的刚度，并且对结构的动力特性产生影响。故本文主要针对活塞处于高位状态时，内压作用与否对煤气柜模态分析。

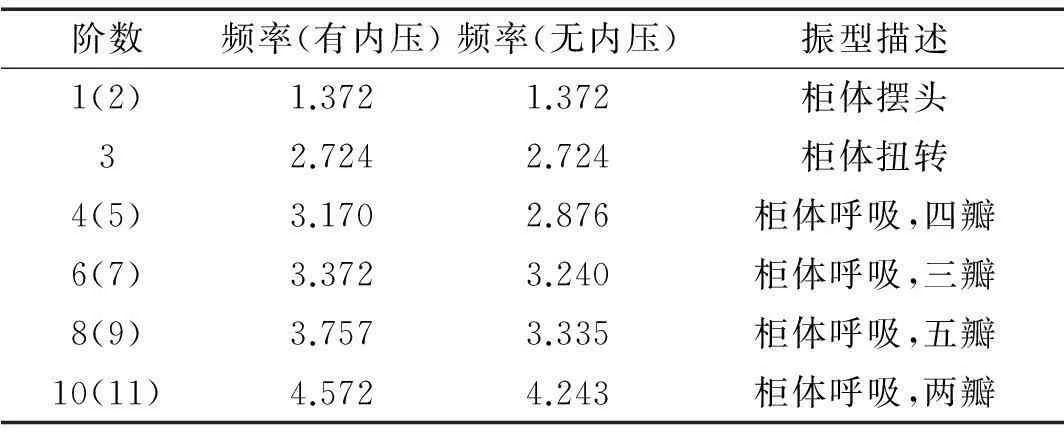
表4　新型煤气柜结构的自振频率

表4为活塞在高位状态下，考虑内压与未考虑内压煤气柜结构的频率与振型特点描述(由于振型相似及篇幅原因内压作用下的振型截图不再给出)。从表4可以看出，考虑内压对煤气柜的平动振型和扭转振型几乎没有影响，有内压和无内压的平动频率和扭转频率均相同；而内压对柜体壳体局部振动影响较显著，考虑内压的影响，壳体振动的频率要比不考虑内压最大增加12%左右。由此可知，柜体内部气压对其局部刚度影响显著，而对整体刚度几乎没有影响。

2背景-共振响应振型能量参与系数

2.1脉动风振响应振型叠加原理

对于新型煤气柜结构在外施动力荷载作用下的动力方程为：

(1)

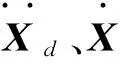
结构振型矩阵Φ=[φ1,φ2,…,φn]，且ΦTM Φ=I(其中I为单位矩阵)，则ΦTK Φ=Ω2(其中Ω为结构前n阶圆频率组成的对角矩阵，即diag[ω1,ω2,…,ωn]结构在脉动风作用下的位移响应方差矩阵为[15]：

LTΦH*T(ω)ΦTdω

(2)

式中，SPP(ω)测压点脉动风压时程互谱矩阵；H(ω)为频响函数矩阵，且H(ω)=[H1(ω),H2(ω),…,Hn(ω)]，其中，Hj(ω)为第j阶模态的频响函数。

2.2背景响应及其能量参与系数的计算

将脉动风作用下的结构振动看作静力过程，即不考虑结构的动力效应，可得到结构总的背景响应及各振型的背景响应。

(1)总背景响应

脉动风作用下，总的背景响应Xb可表示为：

KXb=LPd(t)

(3)

Xb的方差可表示为：

(4)

式中，XP为静力平衡方程KXb=L的解；b为背景响应。

(2)振型背景响应

设Xb=ΦQb，将其代入式(3)，并对等式左右同时左乘ΦT，那么式(3)可改写为：

Ω2Qb=ΦTLPd(t)

(5)

得到：

Qb=H0ΦTLPd(t)

(6)

则第j阶模态背景响应为：

qb,j=Hj,0φTjLPd(t)

(7)

第j阶模态对总背景响应的贡献为：

Xb,j=φjHj,0φTjLPd(t)

(8)

振型位移Qb的方差为：

(9)

式中，第j阶模态背景响应的方差为：

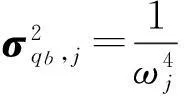
(10)

(3)背景响应振型能量参与系数

脉动风荷载在背景响应上做的功为：

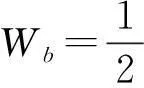
(11)

式中，∑diag[]表示矩阵的对角元素之和。

对背景响应功Wb取数学期望，得到

(12)

脉动风荷载在第j阶模态背景响应上做的功为：

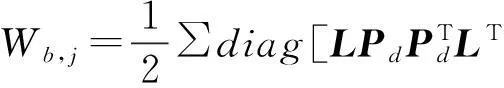
(13)

对在第j阶模态背景响应功Wb,j取数学期望，得到：

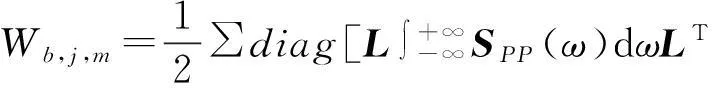
(14)

第j阶振型背景响应的能量参与系数是：

(15)

由式(15)可知，背景响应的振型能量参与系数反映了振型位移对总背景响应位移的平均贡献率。背景响应位移计算值的精度可通过振型累积参与系数以及振型参与系数来控制。

2.4共振响应及其能量参与系数的计算

共振响应是指脉动风荷载在共振频率处激起的结构振动，对第j阶振型的运动方程两侧进行傅里叶变换，得到第j阶振型响应的频域解为：

qj(ω)=Hj(ω)φTjLPd(ω)

(16)

第j阶振型的共振响应为：

qr,j(ω)=Hj(ω)φTjLPd(ωj)

(17)

式中，下标“r”表示共振响应；Pd(ωj)为脉动风压傅里叶谱值在第j阶振型频率ωj处的取值。

第j阶振型共振响应的位移方差为：

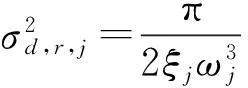
(18)

式中，下标“d”表示位移响应；ξj为第j阶模态阻尼比；SPP(ωj)为脉动风压功率谱在第j阶模态频率ωj处的取值。

第j阶振型共振响应的速度方差为：

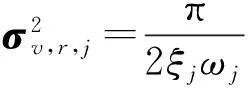
(19)

式中，下标“v”表示位移响应。

脉动风荷载在第j阶振型共振响应上的功等于第j阶振型的动能和弹性能之和：

(20)

对Wr,j取数学期望，得到：

(21)

共振响应总能量，从理论上来说等于全部模态共振响应的能量之和，但当结构自由度十分庞大时，共振总能量很难得到。因此，为了方便起见，将共振能量参与系数定义为各阶共振响应能量与背景响应总能量之比，如下式：

(22)

3煤气柜主要贡献模态选取

新型煤气柜为轴对称结构体系，因此对其进行风振响应频域分析时仅考虑0°风向角情况，本文运用线性滤波AR模型法[16]对脉动风速进行模拟，模拟结果见图6～图7。

图6　脉动风时程曲线 Fig.6 Turbulence wind velocity time-history curve

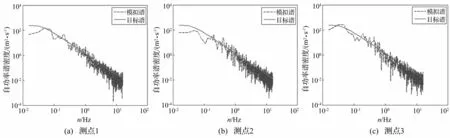
图7　模拟风谱与目标谱的比较 Fig.7 The target spectrum and simulation spectrum

3.1煤气柜背景响应主要贡献模态

由于煤气柜内部活塞上下移动而造成结构体系动力特性的时变性，因此本文首先给出活塞三个典型位置即高位、中位、低位前100阶背景响应能量参与系数，见图8。前文分析可知，煤气柜内部气压对结构模态影响较大，因此以下工况分析均与实际情况相同即考虑内部气压对结构的影响。

接下来分别对三种工况的背景响应能量参与系数按照降序排列，并进行累加计算。当背景响应振型能量参与系数<2%，并且累积系数使之>90%时，对背景响应主要贡献模态选取结束，筛选结果见图9。

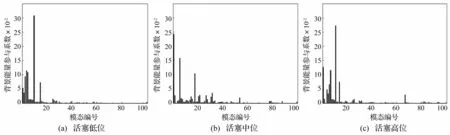
图8　背景响应能量参与系数 Fig.8 The mode energy participation factorof background response

图9　背景响应主要贡献模态 Fig.9 The natural modes with significant contribution to background response

3.2煤气柜共振响应主要贡献模态

分别给出三种工况下的共振能量参与系数，见图10。与背景响应主要模态选取原则不同，对共振响应主要贡献模态选取时，当共振能量参与系数<2%时即可结束筛选，这主要是因为在计算共振能量参与系数时，所用归一化系数为背景响应总能量值，这将造成共振累积能量很难达到90%以上，筛选结果见图11。

需要注意的是，本文风荷载的采样频率为16Hz，所以在对共振主要模态的选取时，仅能考虑频率低于16Hz的模态，对于频率大于16Hz的模态，随着模态阶数的增加，其频率越来越大，相对低频的荷载，越来越难以激起高阶模态的共振，因此高阶模态共振响应越来越小，可以忽略。

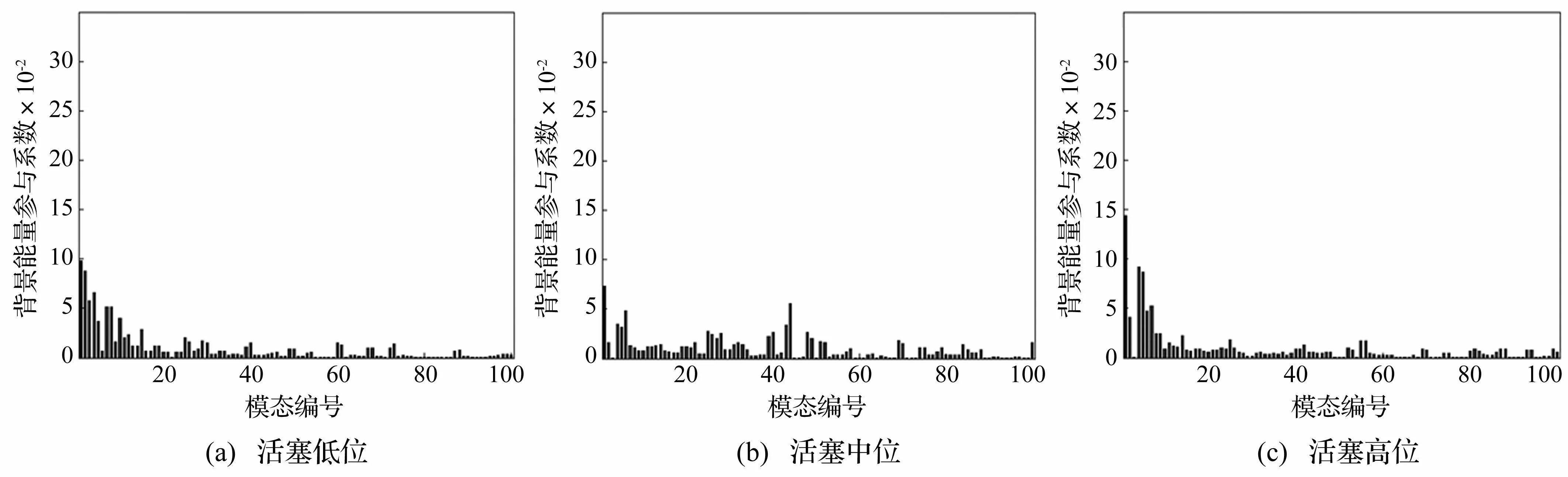
图10　共振响应能量参与系数 Fig.10 The mode energy participation factor of resonant response

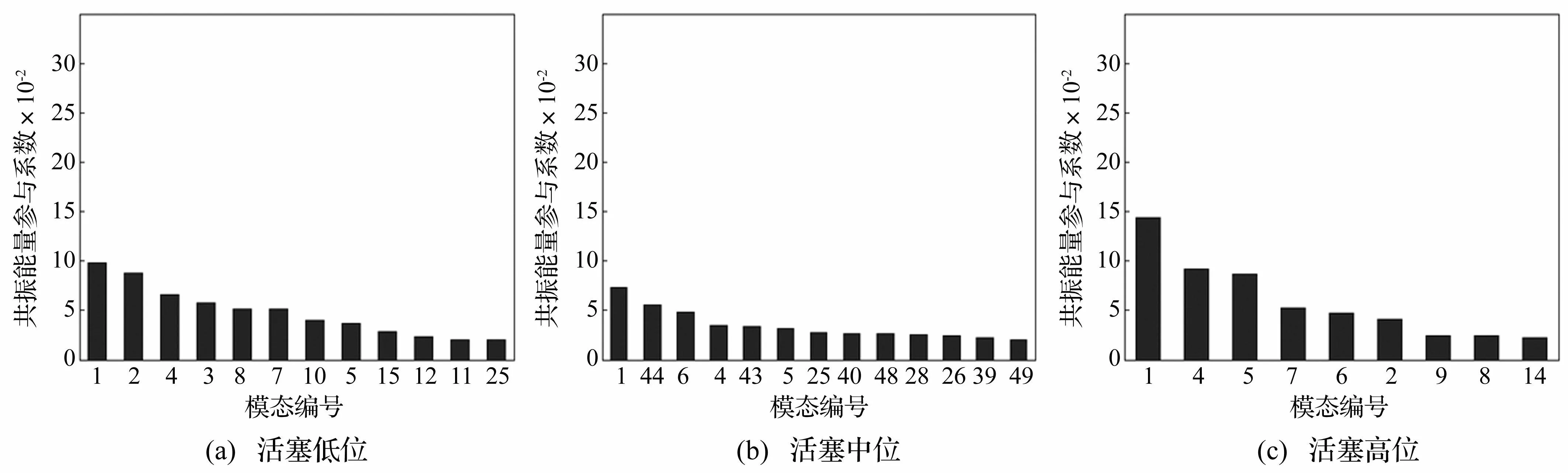
图11　共振响应主要贡献模态 Fig.11 The natural modes with significant contribution to resonant response

对于共振响应能量，由图11分析可知，筛选出的主要模态对共振响应总能量的贡献都不大，这主要是两方面造成的：结构模态分布密集，脉动风压能够激起多阶模态的振动，这可以理解为多阶模态均摊了共振响应总能量；由于结构局部模态刚度较大，各局部模态自振频率与脉动风荷载频率相差较远，使得脉动风荷载无法激起某阶模态的较大共振。

为了验证上述模态选取方法的准确性，本文首先采用完全二次振型叠加法(CQC法)按式(2)分别计算三种工况下煤气柜在脉动风作用下的总响应，并将前100阶模态计算得到的位移均方根作为准确值。接着按上述方法识别煤气柜主要贡献模态，并通过其进行频域分析。最后，给出按上述两种方法计算得到的结构典型位置测点(高度100.8m)的脉动响应均方根值，见图12。

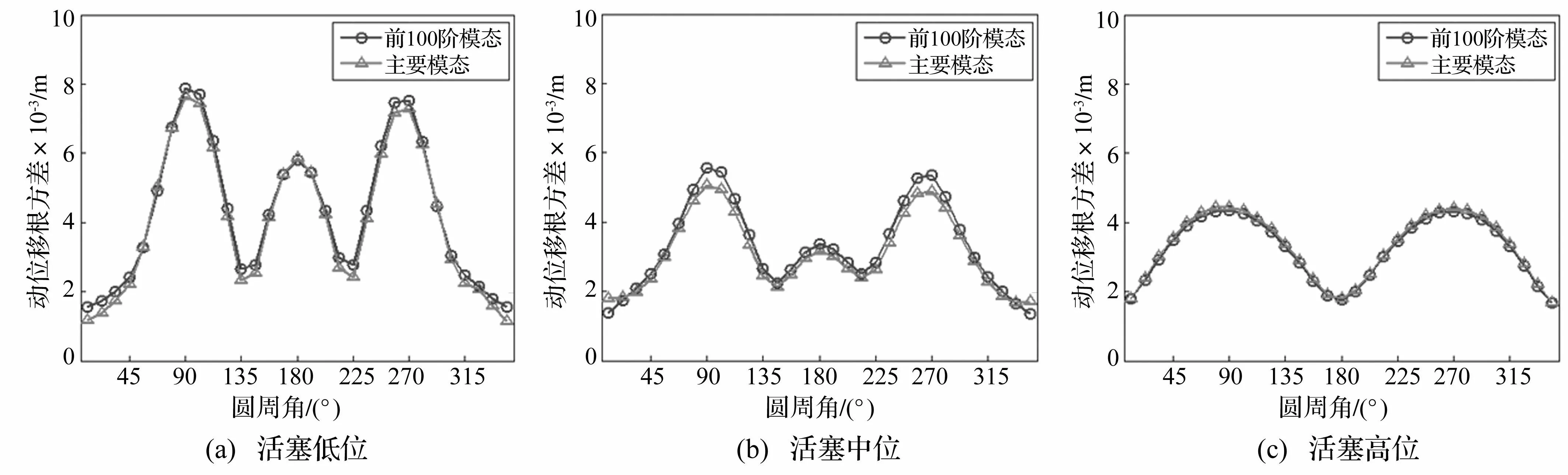
图12　CQC法与振型能量参与系数法的结果 Fig.12 The results of CQC method and mode energy participation factor method

图13　振型能量参与系数法的计算效率 Fig.13 The efficiency ofmode energy participation factor method

结果表明，三种工况下，分别通过主要模态与前100阶模态进行频域分析的结果吻合很好，证明主要贡献模态选取合理，准确。

为了验证通过主要贡献模态进行结构频域分析的计算效率，本文给出了煤气柜6个典型测点在三种工况下参与计算的主要贡献模态数不同，其分析结果与标准值的比值，见图13。

结果表明，随着主要贡献模态数的不断累加，分析结果迅速收敛，这比传统的频域分析方法效率更高，且计算精度可以通过调整筛选原则控制。对于这种自振频率密集，参振模态多的结构体系，振型能量参与系数能够很好的识别主要模态。

4结论

(1)活塞位置对新型煤气柜动力特性的影响显著，随着活塞位置降低，煤气柜自振频率逐渐变大。

(2)煤气柜在活塞高位和中位状态下，一、二阶振型为x,y方向的悬臂梁式振动，第三阶振型为结构的扭转振动；不同于高位和中位振型，低位的一阶振型为环向四个波形的壳体振动，第二、三阶振型为悬臂梁式振动，柜体的扭转振动出现在第18阶，其余各阶局部振动。

(3)内压对煤气柜的平动振型和扭转振型几乎没有影响，而内压对柜体壳体振动影响较显著，考虑内压的影响，壳体振动的频率要比不考虑内压最大增加12%左右。

(4)脉动风振响应的计算精度与模态选取密切相关，模态的选取取决于各阶模态响应对总响应的贡献大小。背景能量参与系数法能够准确识别出煤气柜脉动风振响应的主要贡献模态。

(5)通过调整筛选原则，可以对煤气柜频域分析计算精度进行控制，进而能有效提高频域分析效率。

参考文献

[1]沈世钊.大跨空间结构的发展—回顾与展望[J].土木工程学报,1998,31(3):5-14.

SHEN Shi-zhao. Development Of Long-Span Structures—A Review And Prospect[J]. China Civil Engineering Journal,1998,31(3):5-14.

[2]Wilson E L, YUAN Ming-wu. Dynamic analysis by direct superposition of Ritz vectors [J]. Earthquake Engineering and Structural Dynamics, 1982(10):813-821.

[3]顾明,黄鹏,周毅,等.北京首都机场3号航站楼风荷载和响应研究[J].土木工程学报,2005,38(1): 40-44.

GU Ming, HUANG Peng, ZHOU Yi,et al. A study on wind loads and responses of terminal 3 at beijing capital airport [J]. China Civil Engineering Journal, 2005,38(1):40-44.

[4]王国砚,黄本才,林颖儒,等.基于CQC方法的大跨屋盖结构随机风振响应计算[J].空间结构,2003,9(4):22-26.

WANG Guo-yan, HUANG Ben-cai, LIN Ying-ru. Solution of wind induced random vibration of large span roof structures based on CQC method[J]. Spatial Structures,2003,9(4):22-26.

[5]Nakayama M, Sasaky Y, Masuda K, et al. An efficient method for selection of vibration modes contributory to wind response on dome like roofs[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 73(1):31-43.

[6]Wu Y, Zhang J S, Chen B, et al. Identification of the dominant vibration modes of single-layer reticulated shells under wind action[J]. International Journal of Space Structures, 2007, 22(2):123- 132.

[7]何艳丽,董石麟,龚景海. 空间网格结构频域风振响应分析模态补偿法[J].工程力学,2002,19(4):1-6.

HE Yan-li, DONG Shi-lin, GONG Jing-hai. Wind-induced response of spatial structures with mode compensation in frequency domain[J].Engineering Mechanics,2002,19(4):1-6.

[8]胡继军,网壳风振及控制研究[D].上海:上海交通大学,2000.

[9]Mataki Y, Iwasa Y, Fukao Y, et al. Wind induced response of low-profile cable-reinforced air-supported structures [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1988, 29:253-262.

[10]邓华,董石麟,何艳丽,等.深圳游泳跳水馆主馆屋盖结构分析及风振响应计算[J].建筑结构学报, 2004, 25(2):72-78.

DENG Hua, DONG Shi-lin, HE Yan-li, et al. Behavior analysis and wind-induced vibration computationof mail hall roof structure of shenzhen swimming and diving hall[J]. Journal of Building Structures,2004,25(2):72-78.

[11]田玉基,杨庆山,范重,等.国家体育场大跨度屋盖结构风振系数研究 [J]. 建筑结构学报, 2007, 28(2): 36-41.

TIAN Yu-ji, YANG Qing-shan, FAN Zhong, et al. Gust factors for large-span roof of the national stadium[J]. Journal of Building Structures,2007,28(2):36-41.

[12]Ashraf Ali M, Gould P L. On the resonant component of the response of single degree of freedom systems under wind loading [J]. Engineering Structures, 1985, 7(4): 280-292.

[13]陈波, 武岳, 沈世钊. 背景响应、共振响应定义及其相关性分析方法 [J]. 振动工程学报, 2008, 21(2):140-145.

CHEN Bo, WU Yue, SHEN Shi-zhao. Definitions and correlation analyses for background response and resonant response[J]. Journal of VibrationEngineering, 2008, 21(2):140-145.

[14]田玉基,杨庆山. 大跨度屋盖结构脉动风振响应的参与振型[J]. 哈尔滨工业大学学报,2009(6):146-149.

TIAN Yu-ji, YANG Qing-shan. Dominant modes of fluctuating wind-induced response for large-span roof [J]. Journal of Harbin Institute of Technology,2009(6):146-149.

[15]方同.工程随机振动[M].北京:国防工业出版社,1995.

[16]舒新玲, 周岱.风速时程AR模型及其快速实现[J].空间结构, 2003, 12(9): 27-32.

SHU Xin-ling, ZHOU Dai. AR model of wind speed timeseries and its rapid implementation[J].Spatial Structures,2003,12(9):27-32.

第一作者刘均男，副教授，1976年8月生