基于WMRMR的滚动轴承混合域特征选择方法

基于WMRMR的滚动轴承混合域特征选择方法

戴豪民，许爱强，李文峰，孙伟超

(海军航空工程学院飞行器检测与应用研究所，山东烟台264001)

摘要：为充分利用时域、频域以及时频域中的有效特征，提高滚动轴承故障诊断准确率，提出一种混合域特征集构建方法，利用原始信号分别生成时域和频域特征集，通过经验模式分解提取固有模态函数的排列熵和Hilbert谱的奇异值作为时频域特征集，使得混合域特征集比单域特征更能全面准确反映轴承运行状态。针对混合域特征集存在维数过高、特征之间冗余性严重的问题，采用加权最大相关最小冗余的特征选择方法，以支持向量机分类正确率为依据，选取7个有效特征向量。实验结果表明：基于WMRMR的混合域特征选择方法的分类准确率可达98%，能够有效的识别轴承故障信息。

关键词：混合域；经验模式分解；Hilbert谱奇异值；排列熵；加权最大相关最小冗余

中图分类号:TN911.7；TH165

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.19.009

Abstract:In order to improve the accuracy of rolling bearings fault diagnosis by making full use of effective features in time domain，frequency domain and time-frequency domain, a mixed domain feature construction approach was proposed. With it, time domain and frequency domain features were generated using the original signals, permutation entropies of intrinsic mode functions obtained with EMD and singular values of Hilbert spectrum were extracted as time-frequency domain feature sets, and mixed domain feature sets were made to more fully and accurately reflect bearing running states than the single domain features do. Aiming at mixed domain feature sets having shortcomings of too high dimensions and serious redundancy, a feature selection method based on weighted minimal redundancy maximal relevance (WMRMR) was proposed, it could select seven major feature vectors based on the classification accuracy of support vector machine. The test results showed that the classification accuracy of mixed domain feature selection can reach 98% based on WMRMR, and it can effectively identify the bearing fault information.

基金项目：国家自然科学基金(11202162);中国博士后科学基金(2014M560803)

收稿日期：2014-11-25修改稿收到日期：2015-03-31

Fault diagnosis of rolling bearings in mixed domain based on WMRMR

DAIHao-min,XUAi-qiang,LIWen-feng,SUNWei-chao(Institute of Aircraft Detection and Application,College of Naval Aeronautical and Engineering, Yantai 264001, China)

Key words:mixed domain; empirical mode decomposition (EMD); singular values of Hilbert spectrum; permutation entropy; weighted minimal redundancy maximal relevance (WMRMR)

滚动轴承发生故障时常会引起非线性、非平稳振动，对其故障进行诊断的关键是如何从非线性、非平稳信号中提取典型故障特征信息[1]。目前，针对非平稳信号的时频域分析方法，如小波变换[2]和经验模式分解[3](Empirical Mode Decomposition，EMD)，已经广泛应用于旋转机械故障诊断中。但是，作者对西储大学轴承数据中心提供的实测数据[4]仿真发现，时频域特征提取方法有时并不能达到理想的诊断效果。由于单域特征难以全面、准确地刻画出复杂机械系统不同类型的故障特性，本文提出一种混合域故障诊断方法，充分利用时域、频域、时频域典型故障特征信息，使得混合域特征集比单域特征更能全面准确反映轴承运行状态。针对混合域特征集存在维数过高、特征之间冗余性严重等问题，采用加权最大相关最小冗余(Weighted Minimal Redundancy Maximal Relevance，WMRMR)的特征选择方法，以支持向量机(Support Vector Machine，SVM)的分类正确率为依据，实现特征的有效选择。

1混合域特征集的构成

1.1时域和频域特征集生成

时域指标是一种比较直观的信号特征，可以通过观察信号的时域统计特征来辨别轴承故障。本文主要引进6个常用的特征量以及文献[5]提出的2个特征量TALAF指标和THIKAT指标，组成8维时域特征向量构成时域特征集。

时域特征所能提供的信息量是非常有限的，轴承在发生故障时，振动信号的频域中也蕴含了大量的对诊断有用的信息，可以通过傅里叶分析方法将其提取出来。本文主要引进3个常用的特征量构成频域特征集。

时域、频域特征向量见表1，其具体定义可以参见文献[5-6]。

表1　时域、频域特征集

1.2时频域特征集生成

轴承故障的重要信息往往包含在瞬态信号或突变信号中，而单一的时域或频域特征只能对信号进行整体刻画，不能同时对信号进行局域性分析。基于EMD的时频分析方法可以从不同尺度对信号的局部特征进行描述，能够准确的刻画信号的时频特性。为了较全面的描述振动信号的时频域特征，本文从能量和复杂度两个层面，分别选取Hilbert谱奇异值和固有模态函数(Intrinsic Mode Function，IMF)的排列熵(Permutation Entropy，PE)作为时频域的特征向量。

1.2.1基于Hilbert谱奇异值的时频域特征

Hilbert谱作为轴承振动信号的一种时频域表示方法，描述了信号的幅值在整个频率段上随时间和频率的变化规律，同时Hilbert谱也包含了轴承信号大量的特征信息[7]。对Hilbert谱进行奇异值分解，将得到的奇异值作为特征向量，也是一种有效的特征选择方法[8]。考虑到轴承故障信息主要包含在前几个较大的奇异值中，本文选取Hilbert谱中前5个奇异值构建时频域特征向量TF1=[λ1,λ2,λ3,λ4,λ5]。

1.2.2基于IMF排列熵的时频域特征

复杂度是刻画非线性时间序列的一个重要指标，它反映了信号序列的混乱程度[9]。轴承正常运行时，其波形为平稳的随机信号。轴承出现故障时，由于激起系统的共振频率，振动信号会变得越来越复杂，越来越不平稳。从时域的角度上看，其波形将会产生新的振动模式或状态；从频域的角度上看，其频率结构发生了改变，产生新的频率成分。复杂度正是反映了一个时间序列随着序列长度的增加出现新模式的速率。因此，一个时间序列的复杂度能够描述出系统状态发生变化的情况。所以从这个意义上来说，可以用复杂度刻画轴承振动信号随时间变化的状态。

排列熵作为时间序列复杂度的一种度量[10]，可以用来检测时间序列的动力学突变，能够敏感地捕捉轴承振动信号的故障信息，所以本文提取各IMF排列熵作为特征向量，考虑到轴承故障信息主要包含在高频带，计算信号前5个IMF 排列熵，构建时频域特征向量TF2=[PE1,PE2,PE3,PE4,PE5]，其中排列熵的定义为：

(1)

式中，Pj为不同符号序列出现的概率，k=n-(m-1)τ，n,m和τ分别为原始信号的序列长度、嵌入维数和延迟时间。

2加权最大相关最小冗余算法

最大相关最小冗余算法(Minimal Redundancy Maximal Relevance，MRMR)使用互信息衡量特征的相关性与冗余度，并使用信息差和信息熵两个代价函数来构建特征子集的搜索策略[11]。MRMR算法中最大相关和最小冗余的定义分别如式(2)和式(3)所示：

(2)

(3)

结合以上两个测度指标，就可以得到MRMR算法的两个评价函数来指导特征子集的选择，即：

maxΦ1(D,R),Φ1=D-R

(4)

maxΦ2(D,R),Φ2=D/R

(5)

在式(4)中，刻画相关性的互信息值D与刻画冗余度的互信息值R是赋予相同的权重。但是实际应用中，一些特征既具有较大相关性又具有较大的冗余度，MRMR算法对这类特征筛选出的特征子集并不是最佳的。WMRMR通过引入权重因子μ来权衡相关性和冗余性的度量，以获得最好的特征选择结果，相应地MRMR评价函数可以修正为[12]：

maxΦ3(D,R),Φ3=μD-(1-μ)R

(6)

式中，μ的取值范围是0≤μ≤1，当μ=0.5时，式(6)就退化为式(4)的标准MRMR评价函数。

3基于WMRMR的轴承信号特征提取方法

为了验证WMRMR算法所选择的特征子集的优劣，本文采用支持向量机的分类准确率作为评价指标，实验步骤如下：

步骤1选取轴承正常态、内圈故障态、外圈故障态以及滚动体故障态四类样本，每种状态包含50个样本。为了方便对特征进行排序，分别对时域、频域以及时频域特征进行编号，其中，时域特征的有效值、峰值、峭度、峰值因数、脉冲因数、裕度因数、TALAF、THIKAT编号为1～8，频域特征的重心频率、均方频率、频率方差编号为9～11，时频域特征IMF排列熵编号为12～16，Hilbert谱奇异值编号为17～21。

步骤2将权重因子μ以0.1为步长进行赋值，即μi=0,0.1,…1,i=1,2,…,11，采用WMRMR分别得到与权重因子μi对应的一组候选特征集Si。

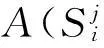
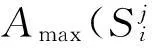
按照步骤1、2即可求取不同权重因子μ对应的特征子集，将特征子集按Φ3(D,R)进行降序排列的结果见表2。

表2　特征降序排列分布

由表2可知，不同权重因子排序后的特征子集的次序是不同的，这表明权重因子能够细致地区分特征的敏感程度。按照步骤3和4采用SVM分类器测试特征子集，并按照特征排序结果逐一添加特征，所得分类正确率的变化情况见图1。

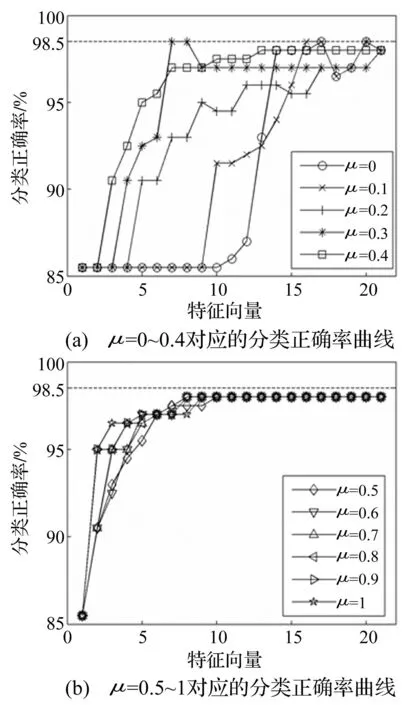
图1　不同权重因子对应的分类准确率曲线 Fig.1 Classification accuracy curves corresponding to different weighting factors

从图1可以看出，随着特征数量的增加，分类正确率首先逐渐增大，当达到一个峰值后，将基本保持不变或下降。这表明峰值之后增加的特征没有改善分类效果，有些反而给分类带来了不利影响。同时，不同权重因子对应的最高分类准确率也不同，当μ=0，μ=0.1，μ=0.3时，可以达到最高分类准确率98.5%，而μ=0.3时达到最高分类准确率所需的特征个数最少，仅为7个，所以本文选取权重因子μ=0.3时对应的前7个特征向量做为最终的特征子集，对应的特征分别是λ1、有效值、重心频率、TALAF、PE1、λ4、λ2。

为了说明本文方法的优越性，参照文献[13]采用核主成分分析方法对原始特征集合进行降维处理，核函数选用高斯核，核参数取100。保留原始数据95%的方差，可将原始特征集降成9维的特征子集，具体结果见图2。将得到的200×9的训练集矩阵输入SVM中训练，采用网格搜索法来获得最佳的分类准确率，其中，网格搜索的范围是[2-8,28]。从图3可以看出，利用核主成分分析选择出的特征子集，其分类准确率最高能达到96.5%。通过以上对比分析可以发现，基于WMRMR的特征选择方法不仅分类准确率更优，而且特征子集的维数更低。

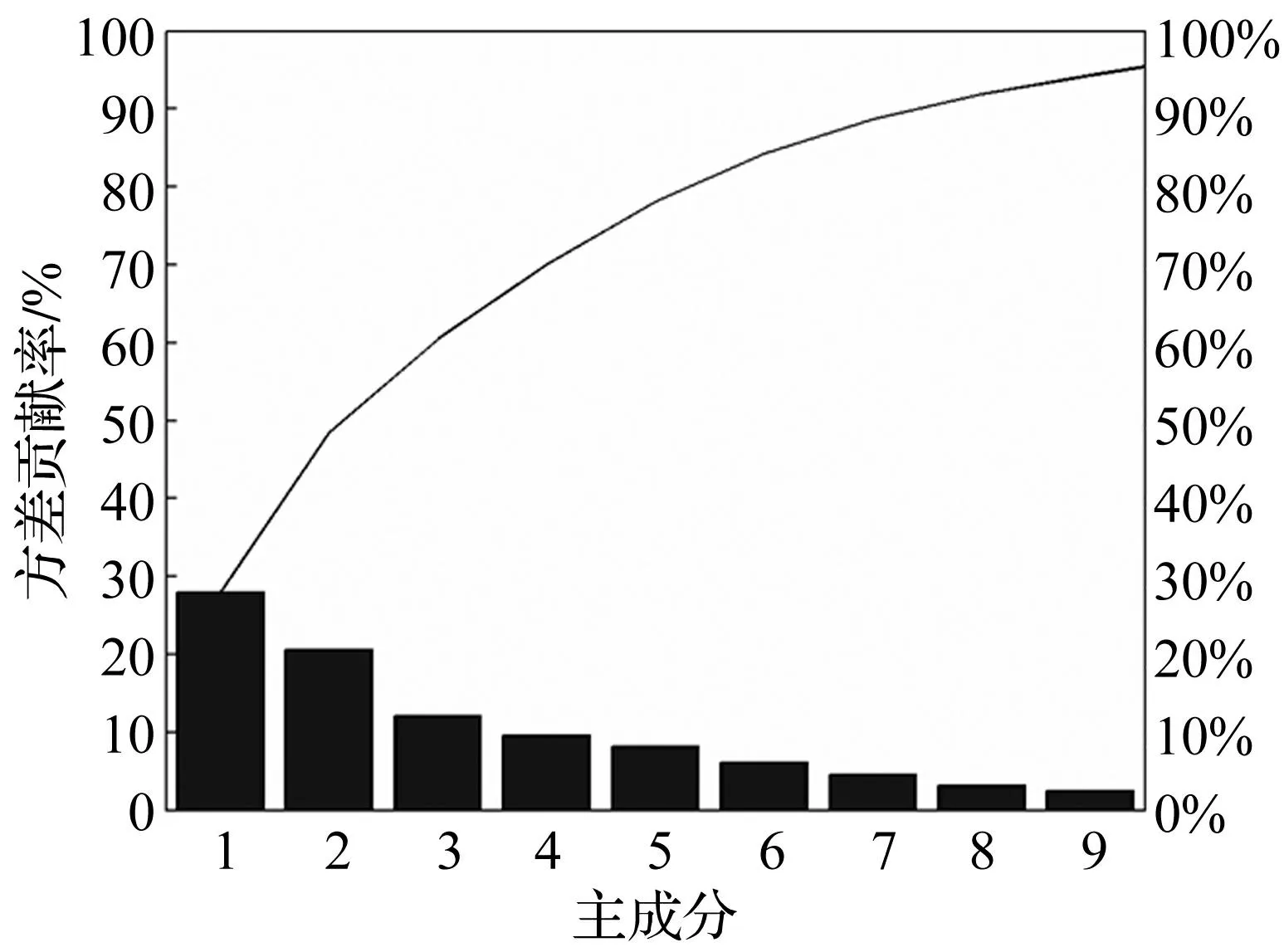
图2　原始特征集核主成分分析结果 Fig.2 The kernel principal component analysis’s result of original feature set

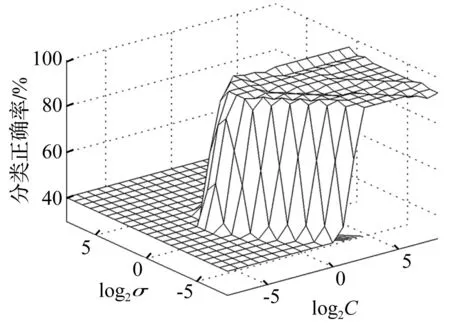
图3　网格搜索分类准确率 Fig.3 Classification accuracy of grid search

4基于支持向量机的轴承故障诊断实例

为了验证2.3小节选择出的混合域特征子集的故障诊断效果，本文仍选取上述四类状态样本进行仿真，其中，每种状态包含100个样本，50个用于SVM训练，50个用于测试。图4是训练集的网格搜索分类准确率，高达99.5%。表3是最终测试集的分类准确率，整体分类准确率为98%。表4是基于IMF排列熵的SVM诊断结果，从这两个表的对比结果可以明显看出：混合域的分类效果要明显优于单一的时频域分类效果。

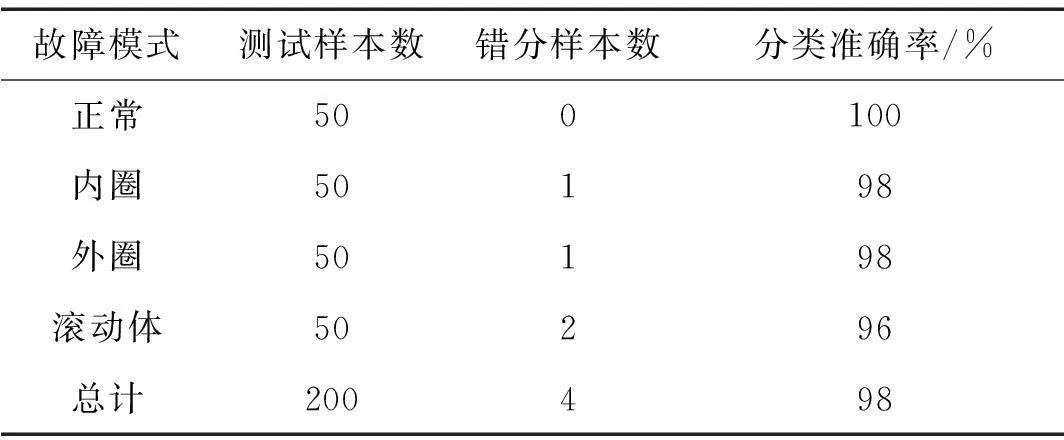
表3　基于混合域的SVM诊断结果

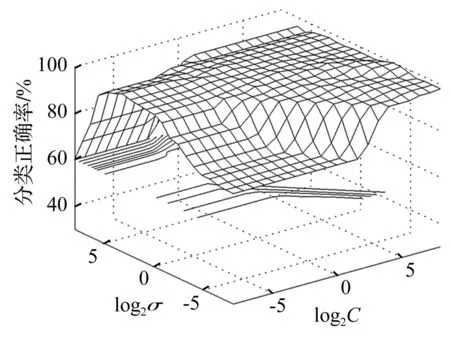
图4　训练集网格搜索分类准确率 Fig.4 Classification accuracy of training set by means of grid search

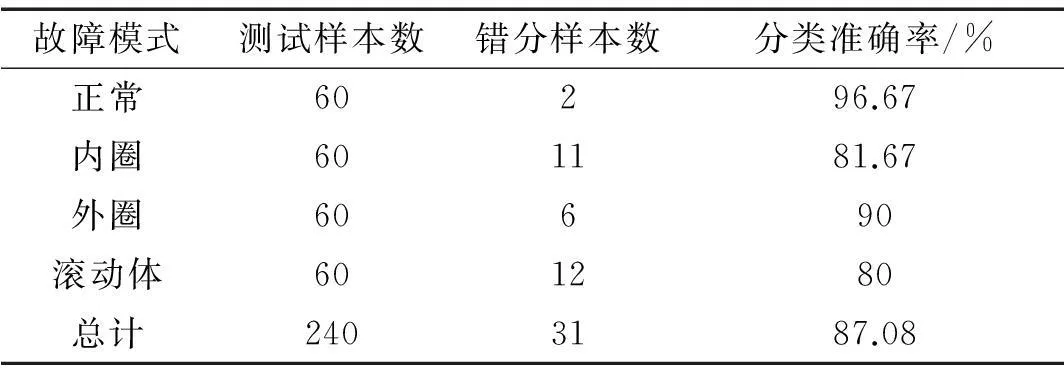
故障模式测试样本数错分样本数分类准确率/%正常60296.67内圈601181.67外圈60690滚动体601280总计2403187.08

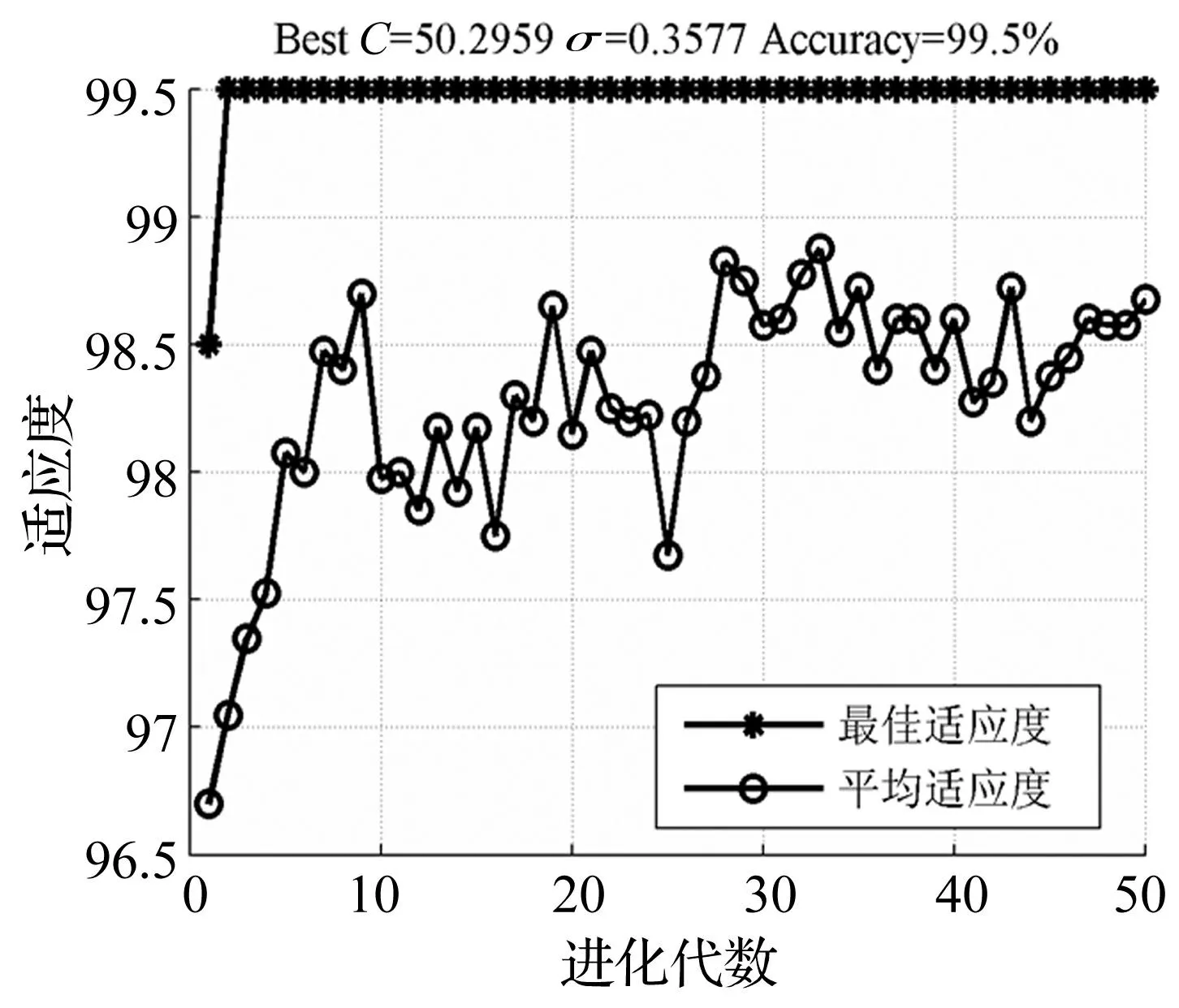
图5　遗传算法参数寻优适应度曲线 Fig.5 Fitness curve of parameter optimization by genetic algorithm

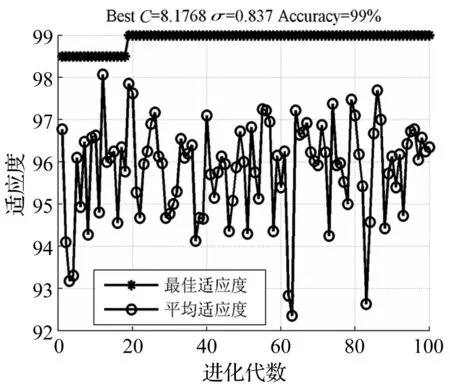
图6　粒子群算法参数寻优适应度曲线 Fig.6 Fitness curve of parameter optimization by particle swarm optimization

为了说明特征选择的重要性，分别采用遗传算法和粒子群算法对SVM进行参数寻优。从图5和图6可以看出，这两种方法可以很“轻松”的使训练集的分类准确率达到99%，这充分说明了特征向量的选择至关重要，“优秀”的特征向量对模式识别起到决定性作用，从另一方面也说明了本文提出的混合域的故障诊断方法能够有效的识别轴承故障信息。

5结论

(1)混合域特征集比单域特征更能全面、准确地反映轴承运行状态。

(2)加权最大相关最小冗余特征选择方法能够有效的提取敏感特征向量，与核主成分分析方法相比，不仅分类准确率更高，而且特征子集的维数更低。

(3)特征向量的有效选择关系到故障诊断效果的好坏，本文提出的基于WMRMR的混合域特征选择方法分类准确率可达98%，能够有效的识别轴承故障信息。

参考文献

[1]Randall R B, Antoni J. Rolling element bearing diagnostics A tutorial[J]. Mechanical Systems and Signal Processing, 2011, 25(2): 485-520.

[2]罗荣,田福庆,李克玉,等.卷积型小波变换实现及机械早期故障诊断应用[J]. 振动与冲击, 2013, 32(7): 64-69.

LUO Rong, TIAN Fu-qing, LI Ke-yu, et al. Realization of convolution wavelet transform and its application in mechanical incipient fault diagnosis[J]. Journal of Vibration and Shock, 2013, 32(7): 64-69.

[3]张超,陈建军,郭迅.基于EMD能量熵和支持向量机的齿轮故障诊断方法[J].振动与冲击, 2010, 29(10): 216-220.

ZHANG Chao, CHEN Jian-jun, GUO Xun. A gear fault diagnosis method based on EMD energy entropy and SVM [J]. Journal of Vibration and Shock, 2010, 29(10): 216-220.

[4]The Case Western Reserve University Bearing Data Center Website [DB/OL]. http://csegroups.case.edu/bearingdatacenter/pages/download-data-file

[5]Sassi S, Badri B, Thomas M. TALAF and THIKAT as innovative time domain indicators for tracking ball bearings[C]//Proceedings of the 14th Seminar on Machinery Vibration, Vancouver, IEEE, 2006: 24-27.

[6]杨国安．滚动轴承故障诊断实用技术[M]．北京：中国石化出版社，2012：65-70.

[7]Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995.

[8]赵志宏,杨绍普,李韶华.基于Hilbert谱奇异值的轴承故障诊断[J].中国机械工程, 2013, 24(3): 346-350.

ZHAO Zhi-hong, YANG Shao-pu, LI Shao-hua. Bearings fault diagnosis based on singular values of Hilbert spectrum [J]. China Mechanical Engineering, 2013, 24(3): 346-350.

[9]饶国强,冯辅周,司爱威,等. 排列熵算法参数的优化确定方法研究[J]. 振动与冲击, 2014,33(11): 188-193.

RAO Guo-qiang, FENG Fu-zhou, SI Ai-wei, et al. Method for optimal determination of parameters in permutation entropy algorithm [J]. Journal of Vibration and Shock, 2014, 33(1): 188-193.

[10]Bandt C, Pompe B. Permutation entropy: a natural complexity measure for time series [J]. Physical Review Letters, 2002, 88(17): 1-4.

[11]Ding C, Peng H. Minimum redundancy feature selection from microarray gene expression data [J]. Journal of Bioinformatics and Computational Biology, 2005, 3(2): 185-205.

[12]李扬,顾雪平.基于改进最大相关最小冗余判据的暂态稳定评估特征选择[J].中国电机工程学报, 2013, 33(34): 179-186.

LI Yang, GU Xue-ping. Feature selection for transient stability assessment based on improved maximal relevance and minimal redundancy criterion [J]. Proceedings of the CSEE, 2013, 33(34): 179-186.

[13]彭涛,杨慧斌,李健宝,等.基于核主元分析的滚动轴承故障混合域特征提取方法[J]. 中南大学学报:自然科学版, 2011, 42(11): 3384-3391.

PENG Tao, YANG Hui-bin, LI Jian-bao, et al. Mixed-domain feature extraction approach to rolling bearings faults based on kernel principle component analysis[J]. Journal of Central South University:Science and Technology, 2011, 42(11): 3384-3391.

第一作者王伟男，博士生，1988年8月生

通信作者周洲女，博士，教授，博士生导师/长江学者，1966年生