航空发动机转子突加不平衡参数分析及LQR控制技术应用

第一作者岳聪男，博士生，1987年7月生

通信作者任兴民男，教授，博士生导师，1960年10月生

航空发动机转子突加不平衡参数分析及LQR控制技术应用

岳聪1,任兴民1， 邓旺群2， 杨永锋1

(1. 西北工业大学力学与土木建筑学院，西安710072；2.中国航空动力机械研究所，湖南珠洲412002)

摘要：为分析航空发动机转子系统升速和正常工作时不平衡突变现象，推导了突变时刻动力参数的瞬时变化以及线性二次型调节器(LQR)在变速转子上的作用过程。通过有限元法和传递矩阵法建立动力涡轮转子瞬态响应分析模型并验证其有效性。研究了支承刚度变化和突变量变化对动力参数瞬时响应变化的影响以及基于主动控制技术下突加不平衡瞬时响应的变化过程。研究发现，支承刚度和不平衡量变化对瞬时突变的参数响应具有一定的影响变化规律，LQR能有效降低突变引起的不平衡瞬态响应。

关键词：航空发动机；转子动力学；突加不平衡；瞬态响应；主动控制

基金项目：国家自然基金(11272257)；航空科学基金(2013ZB08001)；陕西省自然科学基金(2013KJXX-22)

收稿日期：2014-08-04修改稿收到日期：2014-10-11

中图分类号:TH113.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.17.029

Abstract:To analyze aeroengine varying-speed rotor system with sudden mass change in accelerating process and work condition, the instantaneous changing of dynamic parameters and the action process of a linear quadratic regulator(LQR) on the rotor system were derived. Both the finite element method and the transfer matrix method were used to establish the analysis model of the power turbine rotor and its effectiveness was verified. The influences of bearing stiffness, sudden mass change and LQR controller on the transient variation of dynamic parameters were studied. This study showed that bearing stiffness and sudden unbalance change have certain effects on the transient change of dynamic parameters and LQR can effectively reduce the transient response of the rotor system caused by sudden unbalance change.

Parametric analysis due to sudden unbalance change and LQR control application for aeroengine rotor systems

YUECong1,RENXing-min1,DENGWang-qun2,YANGYong-fen1(1. School of Mechanics, Civil Engineering & Architecture, Northwestern Polytechnic University, Xi’an 710072, China;2. China Aviation Dynamical Machinery Research Institute, Zhuzhou 412002, China)

Key words:aeroengine system; rotor dynamics; sudden change unbalance; transient response; active control

转子是航空发动机的核心部件，由于其工作环境恶劣，受力复杂，在运行过程中受到突加不平衡易发生较大的瞬态振动。据不完全统计，某航空发动机仅因这种故障而造成提前更换发动机的比率占17.3%[1]。某航空发动机转子系统抵抗突加不平衡响应以及转子系统是否能再次回复稳定运转的能力，在航空发动机的实际使用过程中有着十分重要的现实功能。

实际涡轮转子升速过程是比较短暂的，更多的不平衡量发生突变都是发生在工作转速时刻，目前对应的高速突加不平衡响应研究还相对较少[2-3]。一些研究学者通常采用阶跃脉冲函数或连续函数两种形式来模拟突加不平衡发生过程时不平衡量的突变过程，并用不同的仿真模型计算了稳定转速下的突加不平衡响应过程。任兴民等[4]研究发现在突加不平衡瞬态响应计算中阶跃响应很大，推导了与突加不平衡响应相适应的传递矩阵。Braut等[5]采用Jeffcott转子模型和四阶Runge-Kutta法对紧急关机后转子不平衡突然增加进行了线性和非线性响应研究。

与此同时，针对突加不平衡响应控制技术的研究也有了一定进展。姚国志等[6]设计了用于转子振动控制用的摩擦板式电流变阻尼器能有效地抑制突加不平衡响应。夏南等[7]分析了雷诺数和系统参数对于转子——挤压油膜器系统突加不平衡响应和加速响应特性的影响。Su等[8]以产生突加不平衡的原理为基础，建立了突加不平衡生成装置模拟试验台并进行了主动平衡试验，将突加不平衡造成的振幅减小了89.6%。Gunter等[9]采用传递矩阵法和改进的有限元程序DyRiBeS对1150MW汽轮机发电机转子系统进行动态分析，开展了线性和非线性转子系统突加不平衡响应的研究。

本文根据某涡轴发动机动力涡轮转子相关数据，在分析瞬时突加不平衡瞬时响应参数获取和验证所建立动力涡轮转子模型准确性的基础上，研究了不同突变量大小和不同突变方位角对参数瞬时不平衡响应的影响以及LQR主动控制技术对不平衡响应突变的控制效果。

1理论分析

1.1不平衡突变瞬时参数

为了说明动力涡轮转子系统涡轮盘突变处前后位置的瞬时变化，图1给出了在某时刻特征圆盘上发生突加不平衡前后稳定旋转位置的变化示意图；图2是以形心重合为标准，将突变前后瞬时稳态位置的形心叠加，观察突变前后物理关系。

图1　不平衡位置突变示意图 Fig.1 Sudden change mass on unbalanced position

图2　不平衡突变前后位置叠加 Fig.2 The superposition of unbalance position

在图1～图2中，XOY是固定坐标系，ξGη是惯性坐标系，G是不平衡截面处的形心，c是质心位置，c′是突变后不平衡量的质心，Gc表示初始不平衡偏心距。GΔc是突变不平衡量偏心距，Gc′为突变后的偏心距。φ(θ)表示初始不平衡量与突变后不平衡量的夹角，θ(t)为瞬时相位角，ψ(t)为瞬时进动角。不平衡突变时转子系统的瞬时位置和不平衡量发生了改变，表现为ψ(t)和θ(t)的瞬时改变。突变先后各变量的对应关系为：

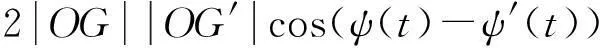
利用上述关系，得到挠度的瞬时变化值

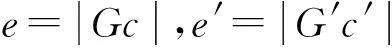
(1)

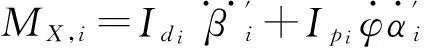
(2)

(3)

(4)

通过计算式(4)，就可以得到突变后涡轮盘动力参数随时间变化的表达式。

1.2LQR控制技术

对于某具有4n个自由度的转子系统，运动微分方程可以描述为如下形式[11]：

(5)

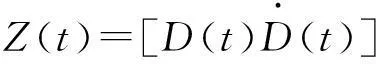
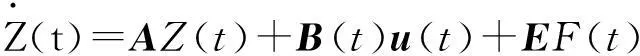
(6)

式(6)是8n维的状态方程，其中

式中：Bs为系数矩阵，一般为单位矩阵。u(t)为控制力作用矩阵，其求解的二次型能泛函数[12-13]可表示为

(7)

一般情况下，假定加权矩阵Q(t)，R(t)为定常矩阵，记Q(t)=Q，R(t)=R。上式所求的最优控制就是得到J最小时的控制矩阵u(t)。为了达到最优控制目的，构造如下Hamilton函数：

λ[AZ(t)+Bu(t)+DF(t)]

通过求导方法即可求得最优控制信号u(t)为：

u(t)=-R-1BTP(t)Z(t)

其中：P(t)矩阵即为Riccati方程的解：

P(t)BR-1BTP(t)-Q

(8)

上式一般是多个互相耦合的非线性方程组，除特殊情况外是不存在解析解。通常令tf→∞来求解u(t)的稳态解。于是有：

PA+ATP-PBR-1BTP+Q=0

上式称作代数Riccati方程，求解形式为

ATXE+ETXA-

(ETXB+S)R-1(BTXE+ST-Q)=0

(9)

式(9)中矩阵X就是代数Riccati方程的解。R为残留矩阵的Frobenius范数。根据上式的解就可以求得最优控制信号u(t)，将u(t)分解为阻尼矩阵和刚度矩阵分别赋予到式(5)中，即可求得LQR作用下系统响应曲线。

2动力涡轮转子临界转速计算

本文分别通过旋转动力学专用的有限元分析软件SAMCEF/ROTOR 和数值仿真算法计算所建立模型的临界转速以验证其准确性。

在SAMCEF/ROTOR平台下，按照图纸模型以及相关参数，使用梁单元模型对涡轴发动机动力涡轮转子结构建立有限元模型。考虑到转子的复杂性，有如下简化：①动力涡轮转子共有4个支承，中间两支承分别与挤压油膜阻尼器并联工作;②由于测扭轴质量较小，且不传递动力，不考虑其转动惯量，将其分作六个集中质量附加到涡轮轴上；③分支处的花键当做刚性连接处理。有限元模型见图3，临界转速特性坎贝尔图见图4。

为了进一步验证所建立模型的准确性，利用传递矩阵法计算得到模型的前两阶临界转速与有限元法得到结果的比较如表1所示。结果表明，两种算法计算得到的前两阶临界转速误差小于5%，基本保持一致；另一方面，本文计算结果与文献[14-15]所给出的计算值基本吻合，虽然某些部位的刚性不能与发动机完全一致，但可以用来进行实际的不平衡响应分析。

图3　T700动力涡轮转子模型图 Fig.3 Model of T700 turbine power rotor

图4　坎贝尔图 Fig.4 Campbell diagram

计算方法一阶临界转速二阶临界转速有限元法7421r/min13452r/min传递矩阵法7394r/min13817r/min误差0.3%2.7%

3突变瞬时不平衡响应分析

为了研究高转速下动力涡轮转子突加不平衡瞬态响应，本文分别从支承刚度和突变量的变化对突加不平衡响应的影响进行分析。假设两个涡轮盘上存在不平衡量，分别为3.75 g·cm∠180°和5.376 g·cm∠36°，根据式(5)知n=2。利用Newmark-β积分法[11]，积分步长为1×10-3s，升速过程中加速度a为600 rad/s2，在此基础上，模拟在3.5 s时发生突加不平衡，此时转速为动力涡轮转子的设计工作转速(20 000 r/min)。下面分别分析不同支承刚度、不同突变质量大小和方向以及主动控制对工作转速下瞬时不平衡量突变的影响。

3.1支承刚度影响

四个支承的初始刚度系数分别为：k1=7.26×107，k2=4×107，k3=1×107，k4=1.42×107(单位：N/m)。本节讨论了四个支承处刚度系数的变化对工作转速时突加不平衡产生的瞬时动挠度r突变峰值的影响。在允许的变化范围内，以支承3刚度系数为例，其他支承刚度以表2所示的组合，观察随支承刚度变化下，瞬时不平衡量突变引起Δr变化。两级涡轮盘上的瞬时响应见图5～图6。

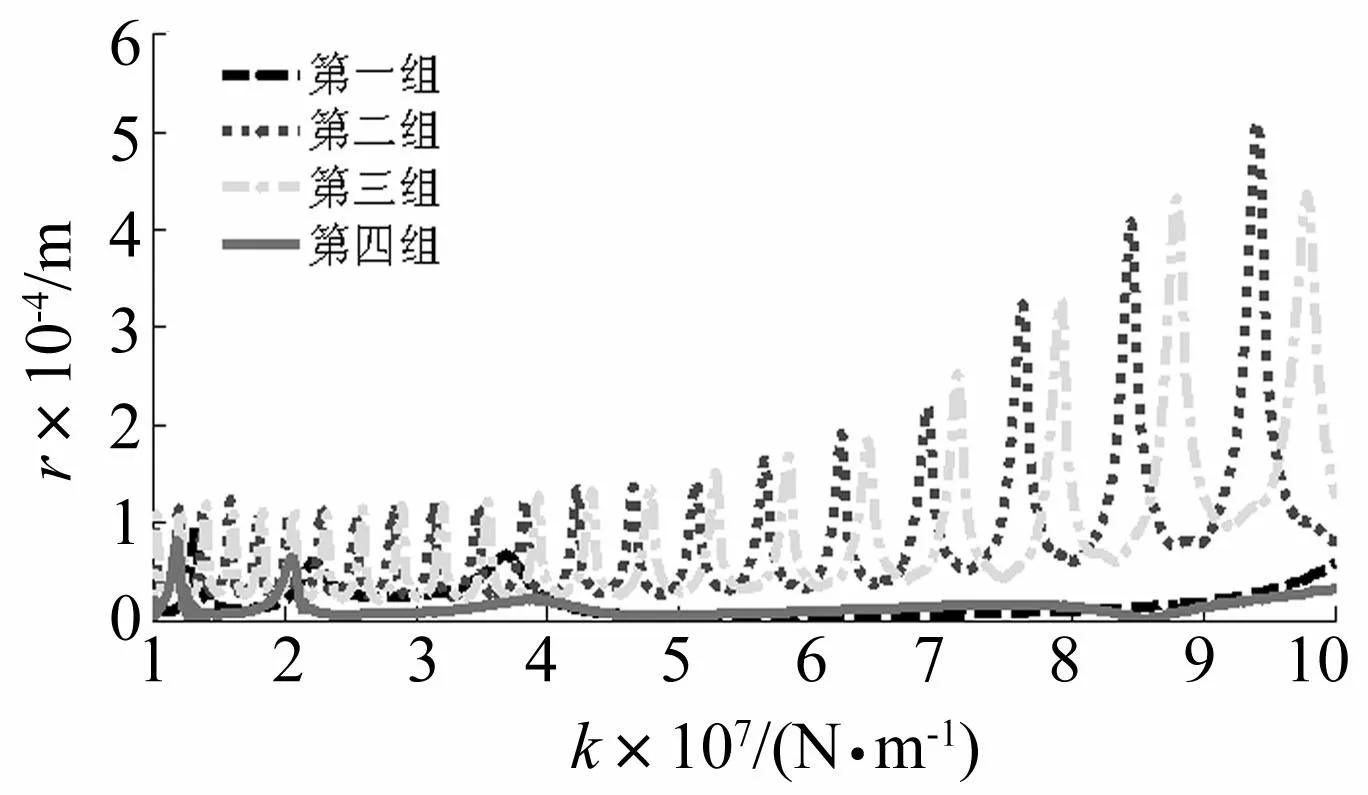
图5　不同刚度下一级涡轮盘突加不平衡瞬时挠度响应 Fig.5 Transient response of deflection under different stiffness combination with sudden change mass on turbine discⅠ

图6　二级涡轮盘突加不平衡动挠度瞬时响应 Fig.6 Transient response of deflection under different stiffness combination with sudden change mass on turbine discⅡ

由于一、四组只有支承2刚度的不同，可以看到支承3刚度在增大时对涡轮盘突变时刻的动挠度响应影响不是很大，对应图5～图6中的响应基本稳定；而二、三组与一、四组相比，突变时刻峰值具有一定的波动周期性。图中的响应曲线表明，随着支承3刚度变化，突变时刻瞬时挠度的峰值变化趋势是基本一致的，而在选取合适的刚度后，瞬时突变不平衡响应带来的幅值变化较小。

表2　不同支承刚度组合(单位：N/m)

3.2突变量大小变化影响

由于涡轴发动机上两个涡轮盘之间的距离较近，仅相隔0.06 m，故两个涡轮盘上的瞬态响应整体变化趋势总体来说基本一致，只是在数值上有些区别，本文仅以一级涡轮盘上的响应为例进行分析。采用3.1节相同的假设，令二级涡轮盘突变后的不平衡量变为8.96 g·cm∠36°；同一时刻，在一级涡轮盘上施加不平衡量，使不平衡偏心距在0～8×10-5m范围内变化，取值间隔为5×10-7m，不平衡方位角0～2π内，取值间隔为π/8。仿真计算得到的一级涡轮盘上瞬时动挠度的变化情况分别见图7。

图7中，随着一级涡轮盘上不平衡量在选定范围内不同，突变时刻的瞬时不平衡响应的幅值大小也会随之发生改变，并且对应一个二级涡轮盘上的突变不平衡量，总有个对应的一级涡轮盘上的不平衡量能将突变带来影响降到最低。

3.3突变瞬时对不平衡响应影响

为了反映不平衡突变瞬时响应的识别，图8中给出了一级涡轮盘在3.2节条件下与无突变下不平衡响应对应时刻瞬时动挠度之差的响应图。从图中可以看到，一级涡轮盘取不平衡方位角为5π/8和13π/8时，突变前后两盘上的瞬态响应差接近0，当不平衡方位角在0和π附近时，突变前后瞬态响应之差最大。

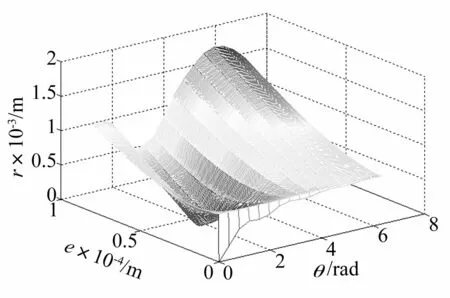
图7　一级涡轮盘瞬时动挠度变化 Fig.7 Transient deflection change on turbine discⅠ

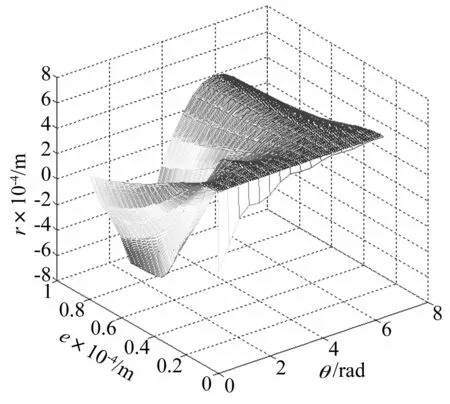
图8　一级涡轮盘不平衡突变前后瞬态响应差 Fig.8 Difference between the amplitude response before and after sudden change unbalance on turbineⅠ

3.4LQR控制应用

为了验证主动控制技术对不同支承刚度下突加不平衡响应的抑制作用，现将LQR主动控制方法应用到不平衡响应突变中去。根据涡轮盘的质量和维数，控制权矩阵Q取值与M相近，R则与E相关：

Q=10×diag(6161616161616161)

R=0.1×E8×8

通过式(7～9)得到每个积分时间下的最优控制信号u(t)后求得瞬时动力涡轮转子系统响应。图9给出了动力涡轮转子加速起动越过前两阶临界转速，在1 s发生突加不平衡响应时一级涡轮盘的瞬态响应。从对比的突变响应中可以看到，随着Q、R取合适的系数后，不仅对转子系统越过临界转速的峰值有效控制，同时对突变时刻的瞬时变化有一定的控制作用。

图10显示了表2中第三组所示各支承刚度系数下两级涡轮盘上有主动控制作用下瞬时响应与无控制下突变响应结果的对比。从图10中可以看到，在选择适当Q、R矩阵的参数后，系统对于不同支承刚度下发生突变的瞬时峰值明显得到了抑制，突变幅值波动幅度也控制在一个较小的范围内。

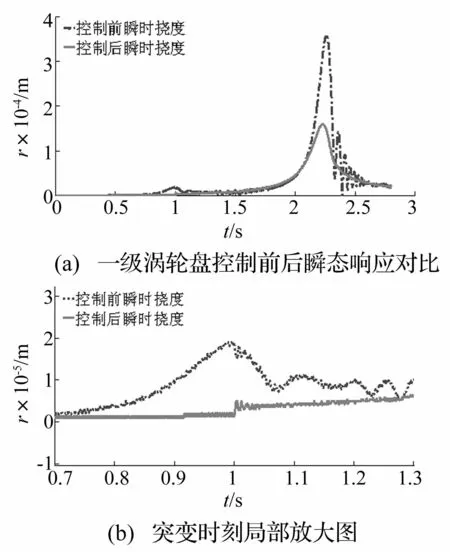
图9　 一级涡轮盘升速过程控制前后 突加不平衡瞬态响应 Fig.9 Unbalance transient response comparison with active control on disc1 in accelerating process

图10　控制前后突变峰值对比 Fig.10 Instantaneous deflection response with LQR controller

4结论

本文给出了转子不平衡量突变瞬时的动力特性参数分析和LQR控制的应用方法，同时利用有限元法和数值仿真两种算法建立了可用于突加不平衡响应分析的涡轴发动机动力涡轮转子模型。研究发现：

(1)不同组合的支承刚度对不平衡量突变的响应有所差别，当设计有恰当的支承刚度时，能有效降低突加不平衡引起的幅值变化；

(2)随着不平衡位置处出现不平衡量突变后，其他位置处的不平衡量大小和方位角均会对突变的瞬时响应产生影响。当达到某个值时，可以消除涡轮盘上不平衡突变量带来的振动影响；

(3)加入LQR主动控制作用后，动力涡轮转子出现突加不平衡现象时，可以将转子系统的参数变化幅值控制在在较小范围内，降低了不平衡突变振动对涡轴发动机动力涡轮转子正常工作的影响。

参考文献

[1]唐洪文，陆永忠，廖道训. 挤压油膜头型转自系统突加质量的响应特性[J]. 华中科技大学学报，2002，30(11): 95-97.

TANG Hong-wen, LU Yong-zhong, LIAO Dao-xun. Characteristics of imbalance response in the sliding bearing-flexible rotor system[J]. Huazhong University of Science and Technology(Nature Science edition), 2002,30(11): 95-97.

[2]Tondl A, Some problems of rotor dynamics[M]. Chapman and Hall,London,1965.

[3]Das A S, Dutt J K, Ray K. Active control of coupled flexural-torsional vibration in a flexible rotor-bearing system using electromagnetic actuator[J]. International Journal of Non-Linear Mechanics, 2011, 46(9):1093-1109.

[4]任兴民，顾家柳.航空发动机转子-支撑系统的突加不平衡响应[J]. 振动工程学报,1991,4(3):57-82.

REN Xing-min, GU Jia-liu.Response of suddenly applied unbalance foraeroengine rotor-bearing systems[J]. Journal of Vibration Engineering, 1991,4(3): 57-82.

[5]Braut S J, Zigulic R, Butkovic M, Numerical and experi-mental analysis of a shaft bow influence on a rotor to stator contact dynamics[J]. Journal of Mechanical Engineering, 2008, 54(10): 693-706.

[6]姚国志，邱阳，方同，等. 多层挤压型电流变阻尼器在转子振动控制中的实验研究[J].航空学报, 1998, 19(5): 570-574.

YAO Guo-zhi,QIU Yang,FANG Tong, et al. Experimental study of a multiple squeeze films electrorh-eological damper for vibration control of rotor system[J]. Acta Aeronautica et Astronautica Sinica, 1998,19(5):570-574.

[7]夏南，孟光，冯心海. 油膜惯性力对双盘栓子SFD系统突加不平衡和加速响应特性的影响[J]. 航空动力学报, 2000,15(1):71-74.

XIA Nan, MENG Guang, FENG Xing-hai. Inf iuence of fluid inertia force on sudden unbalance and accelerating responses of rotor supported on centralized SFD[J]. Journal of Aerospace Power, 2000, 15(1): 71-74.

[8]Su Y R, He L D. Study on online elimination of sudden unbalance-induced vibration using active balancing technology[J]. High Technology Letters, 2012, 16(2): 210-214.

[9]Gunter E J,Chen W J. Dynamic analysis of an 1150MW turbine-generator[J]. Proceedings of the ASME Power Conference,Chicago,2005,Part A:437-443.

[10]顾家柳等编著. 转子动力学[M]. 北京：国防工业出版社, 1988: 46-58.

[11]岳聪,任兴民,邓旺群,等. 基于升速响应信息柔性转子系统的多阶多平面瞬态动平衡方法[J]. 航空动力学报, 2013, 28(11): 2953-2599.

YUE Cong, REN Xing-min, DENG Wang-qun, et al. Multi-plane and multi-critical transient dynamic balance method based on rising speed response information of flexible rotor system[J]. Journal of Aerospace Power, 2013, 28 (11): 2953-2599.

[12]Saptarshi D, Indranil P, Kaushik H, et al.LQR based improved discrete PID controller design via optimum selection of weighting matrices using fractional order integral performance index[J]. Applied Mathematical Modeling, 2013, 6(15): 4253-4268.

[13]Zhang G M, Ou L L, Meng Li, et al. LQR control for homogeneous agents with multi-graph topology[J]. Acta Automatica Sinica,2013,39(6): 913-919.

[14]Burgess G, Rio R. T700 power turbine rotor multiplane/multispeed balancing demonstration[R]. MTI TechnicalReport, NASA Contractor Report CR-159586, Prepared for NASA-Lewis Research Center under Contract No. NAS3-18529, 1979.

[15]Wahon J, Lee C, Martm M. High speed balancing applied to the T700 engine[R]. MTI Technical Report No. MTI87TR56, NASA Contractor Report CR-180899, Prepared forNASA-Lewis Research Center under Contract No. NAS3-23929 and NAS3-24633, March 1989.