土木工程结构全寿命期地震损失成本进展研究

第一作者朱健男，博士后，副教授，1975年生

土木工程结构全寿命期地震损失成本进展研究

朱健1,3，谭平2，周福霖2,金建敏2

(1. 宁夏大学土木与水利工程学院，银川750021； 2. 广州大学工程抗震研究中心，广州510405;3. 长安大学建筑工程学院，西安710064)

摘要：近年来在西太平洋地区发生的一系列重大自然灾害如地震、飓风等给人类社会敲响了警钟，为了应对重大自然灾害的不利影响，世界各国政府都在研究或已经出台了防灾减灾保险法律如地震保险法加以应对，这应该说是防灾减灾研究的一个必然的趋势。而完善的地震保险政策的出台必须建立在工程结构全寿命期地震损失成本研究的基础上。由于我国目前工程结构全寿命期地震损失成本研究等基础应用研究的缺乏导致我国巨灾保险政策迟迟难以推出，基于此,总结和回顾了工程结构全寿命期地震损失成本研究的理论内涵和研究现状，分析了以往工程结构地震易损性研究和全寿命期地震损失成本研究所面临的理论缺陷和应用局限，重点阐述了基于组合的地震易损性研究的理论优势、具体实施步骤和关键技术特点，最后展望了基于此建立我国工程结构全寿命期地震损失成本研究框架体系的重大意义。

关键词：土木工程结构；基于组合的地震易损性；全寿命期地震损失成本；随机分析；蒙特卡洛模拟

基金项目：国家自然科学基金(51468050)；国家重点基础研究发展计划(2011CB013606)；宁夏自然科学基金(NZ13021)

收稿日期：2014-09-01修改稿收到日期：2015-02-05

中图分类号:TH212；TH213.3

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.17.019

Abstract:Earthquake, hurricane and tsunami are main natural risks faces by human society. Recently a series of large natural disasters have occurred in West Pacific area, they warned us. To minimize their negative effects on human society, countries all er the world now introduce or have published disasters insurance policies, this is an inevitable tendency and a best way to minimize seismic or hurricane loss. Now people in China are very eager to have insurance laws to protect their properties, but unfortunately the government has not published a practical natural disaster insurance policy due to lack of fandamental study on life cycle seismic cost (LCSC). Here, the LLSC theory was reviewed and important meaning of LCSC for China society was also presented. Theoretical defects and obstacle in practical application for previous seismic vulnerability research and the LCSC theory were analyzed. An innovative seismic vulnerability study based on assembly was proposed. Its theoretical benefits, technical characters and particular implementation steps including damage analysis and loss assessment in life-cycle were presented in detail. Finally, the significance of establishing the study frame system for life-cycle seismic cost of our country was proposed.

A review of study on life-cycle seismic loss estimation in civil engineering

ZHUJian1,3,TANPing2,ZHOUFu-lin2,JINJian-min2(1. Department of Civil and Hydraulic Engineering, Ningxia University, Yinchuan 750021, China; 2. Earthquake Engineering Research and Test Center, Guangzhou University, Guangzhou 510405, China;3. School of Civil Engineering, Chang’an University, Xi’an 710064, China)

Key words:civil structures; seismic vulnerability based on assembly; life-cycle seismic loss estimation; stochastic analysis; Monte-Carlo simulation

近年来在西太平洋地区发生的一系列重大自然灾害给我们敲响了警钟，给人类社会造成的影响是深远的。2008年发生在中国西部的汶川大地震(Ms8.0)直接经济损失高达8451亿人民币，由于中国没有设立地震等巨灾保险救援制度体系，保险只赔了20多亿，占比0.2%，基本上是靠中央政府举全国之力来进行经济援助[1]；2011年3月11日东日本大地震(Ms9.0)引发的海啸直接导致福岛核电站发生核泄漏的严重事件，人员伤亡近两万人，据台湾媒体报道，美国风险分析业者AIR Worldwide表示，东日本大地震或会致保险损失金额高达近350亿美元，成为史上代价最昂贵灾难，这还未计入海啸造成的损失。这项数额几乎等同2010年全球保险业的整体灾损金额，或会迫使保险市场调高保费[2]；2013年11月8号台风“海燕” 横扫菲利宾造成上万人伤亡，三百多万人无家可归，上千万人受灾，由于菲利宾国力弱小并且没有设立巨灾保险体系，灾区无法得到中央政府的强力援助，海啸造成的损失将导致当地社会的长期衰退。

目前地震等自然灾害对人类社会的影响研究已经转移到了地震灾后恢复重建的研究上，而恢复重建考验的是一个地区或一个国家面对突如其来的自然灾害时的应对能力。以往我国对于地震等自然灾害的灾后重建单纯依靠中央政府不计成本的行政性救援模式应该说是不可持续的，也加重了各级政府的财政负担，从长远来看还是要建立地震等巨灾保险政策，在国际上，巨灾保险赔款一般占到灾害损失的30%～40%，可大大减轻政府和财政的负担。而完善的地震保险政策的出台必须建立在工程结构全寿命期地震损失成本研究的基础上，2014年3月11日，中国保监会主席项俊波在第十二届全国人大会议期间表示，“在我们国家建立巨灾保险制度非常重要也非常紧迫，82%的人民群众支持建立我国的巨灾保险制度，建立完善的适合我国国情的巨灾保险制度是一个世界级的难题”，保监会正在深圳市和云南省分别进行巨灾保险的试点工作，其中在云南省主要开展涉及50万户的农村房屋地震灾害保险研究工作[3]，因此目前我国在工程全寿命期地震灾害损失成本方面的应用基础研究还处于探索阶段。基于此，本文首先回顾了基于性能的地震工程研究的内容和本领域主要研究概念，在此基础上，主要介绍了目前国内外工程结构全寿命期地震损失成本研究的现状、存在的问题以及面临的挑战，重点分析比较了以往基于结构整体或层变形响应的地震易损性方法和基于组合的地震易损性方法的优劣差异，以及对工程结构未来全寿命期地震损失成本评估所产生的根本性影响，并指出本领域未来研究的重点和方向。

1工程全寿命期地震损失成本研究概述

工程全寿命期地震损失成本研究实际上是基于性能设计思想的重要一部分，是基于性能地震工程(PBEE)的必然延续，目前基于性能设计思想的几个重要步骤包括：性能目标的确定、概念设计、设计评估和经济评估在本领域研究中均有体现。基于性能的工程结构全寿命期地震损失成本分析研究也包含了这四个阶段：①地震危险性分析；②工程结构分析；③结构损伤分析；④地震成本损失分析，当然不同学者实现这四步工作的具体分析方法会有所不同，这恰恰体现了基于性能的地震工程研究的发展进步[4]。

最新的全寿命期地震损失成本研究相关的重要概念包括：地震概率危险性研究、性能水平的定义、非线性静态和动态分析方法、易损性分析、参数概率敏感性分析、结构工程和全寿命期经济成本评估等。

其中地震概率危险性研究这项工作首先需要了解建筑抗震规范、工程所在地的地震动参数相关数据和抗震设防烈度等，该研究具体关键参数有：①在全寿命期t内(如50年)地震发生的次数和对应的随机时间点：T1,T2,…；②对应每一个时间点发生的地震震级M和震中距R随机参数值，也是与当地地震活动性相关的随机变量；③确定时间点T1,T2,…上对应的地震震级M和震中距R值后，构建对应的概率随机地震加速度时程记录。研究中需要考虑对于地震激励的随机反应谱特性和瞬时特征值的概率表达，体现强震持时与地震震源类型、地震强度、震中距和建筑物所在场地剪力波速、局部场地条件的内在关联性，为了尽可能全面地预测和描述这些不确定性随机地震波的特征，通过构建合适的概率模型来全面且细致地对未来可能发生的地震时程进行描述是可能的，因此通常采用蒙特卡罗算法基于以上规则建立全寿命期内的地震动随机样本。

对工程结构体系的研究工作主要包括工程材料的力学性能概率研究、构件力学性能概率研究、结构整体力学性能与静动力分析方法的选择和静动力性能研究、以及上述工作的试验研究。通常这项工作和结构损伤研究可以合并为一项连续的系统工作来完成，结构损伤研究工作涵盖了从材料到构件再到整体结构的力学损伤定义、性能水平的分析、损伤敏感性参数的研究、易损性分析等子项研究工作。结构损伤研究通常基于试验模型和有限元数字模型来分别进行，并参考以往的地震房屋损伤实地勘察统计数据和专家个人经验。以往的数字损伤分析限于计算方法和时效、易损性方程建立的方法差异、建模方式和手段、计算要求和精度等的局限，经历了一个概略到精细、从宏观整体渐至微观局部的进化过程。最早国外学者对房屋结构进行地震损失评估采用易损性概率矩阵法(DPM)，该法由Whiteman等[5]在分析整理了发生于1971年的San Fernando大地震后的1600栋房屋损伤数据后于1973年首次提出，该法是建筑结构损伤和经济损失研究中早期基本和实用的经验性方法，主要针对某个地区内多种类型的房屋结构群体进行大范围的未来地震损伤评估和判断，其中尤以现场勘查法直接采集到地震后现场的房屋损伤信息而得到了广泛的应用，1985年又引进了加入专家和工程人员的个人判断和意见的DPM法(ATC13)[6]，然而该方法由于存在以下几项缺点而限制了其进一步应用：勘查到的房屋样本数量不可控制，地区性的房屋建造习俗差异、地震的特征差异以及收集到的严重损伤或倒塌的房屋样本数量不足、人为主观因素等，但该法作为一种基础性的城镇宏观地震损失评估工具近年来仍时有使用，如应用DPM法对巴塞罗纳和里斯本等欧洲城市的地震宏观易损性都有研究[7-8]；Hiroyuki等[9]通过采集当地专家意见调查表的形式对菲利宾马尼拉市区不同类型的房屋建筑群的地震易损性进行了分类分析研究，研究结果被认为接近拟动力Pushover法计算的结果；Martinelli等[10]结合收集到的房屋类型和以往的房屋地震抗震性能数据、GIS地理信息系统和卫星图片信息，对意大利Abruzzo地区的城镇房屋群的地震宏观易损性指数和损伤情况进行了大范围简易评估研究。20世纪90年代开始基于静态拟动力的非线性Pushover推覆法开始流行并引入到ATC40中[11]，该法通过分析结构的概率能力谱和概率需求谱，通过两者交会性能点的概率统计分析来得到结构在不同谱指标区间值下的损伤限值状态概率值，一般损伤限值状态可分为五级：无损伤状态N，轻微损伤状态S，中度损伤状态M，严重损伤状态E和完全损伤状态或倒塌C，进一步可得到结构的概率分析易损性曲线和估算结构的地震损失，该法从实际应用来看已经从早期的经验性方法过渡到基于有明确物理意义的分析性方法，具体来讲该法不仅可以对群体建筑物进行宏观地震损伤评估也可以对单体建筑物进行基于整体或层变形的地震损伤分析。如Barbara等[12]采用Pushover方法对钢筋混凝土结构进行了大批次样本的基于位移的简化随机地震易损性分析；Rossetto等[13]就采用这种基于能力谱的自适应Pushover方法对低层带内填墙的钢筋混凝土群体建筑进行了基于位移变形的地震易损性开创性研究，研究中考虑到了材料和地面运动的不确定性。Li等[14]采用变模态Pushover静态分析法，在考虑结构全生命周期地震成本最小化的原则下，还是依据层间位移角作为损伤评价指标参数提出了对钢结构的优化设计的原则，并通过对一栋9层钢结构的计算做了验证。基于Pushover的拟动力方法相对以前是一个巨大的进步，由于采用谱指标该算法兼顾了效率和精度，尤其是自适应Pushover分析在传统Pushover分析方法的基础上进行了重大改进，在自适应Pushover分析中侧力分布不再是均匀或是倒三角分布并恒定不变，在每一步分析中侧力分布及大小都随着模态形状进行连续的自适应变化，这样就考虑了水平侧推力的大小和分布会随着结构的周期、频率、阻尼和振型的改变而改变的特性，弥补了传统静力增量法的不足。但客观的来讲在Pushover拟动力静态分析中由于假定结构为单自由度体系或简化的多自由度体系，所以很难界定结构在非线性响应中的明确物理内涵。该法无法对实际结构在地震动中的细节部位变形进行辨别如钢筋混凝土框架结构在同一层中不同部位的两根柱或同一部位的不同构件的损伤差异，当然这种方法也在不断地尝试改良中，如Gencturk[15]对传统钢筋混凝土结构和钢纤维混凝土结构(ECC)的全寿命期地震损失成本进行了对比研究，研究中基于push-over方法以结构的层间位移角作为结构整体地震损失成本的主要损伤依据，同时辅助采用了钢筋的应变作为局部结构损伤性能水平的评价指标，相对以前的研究思路就有所进展。随着计算硬件性能的提高，基于实际动力的非线性时程分析方法(THA)或增量动力时程法(IDA)在工程结构地震易损性和全寿命周期损失成本研究中逐步成为另外一种主流技术选择，时程分析方法的优势在于对于工程结构在地震中的每一个细节部位的变形均有具有明确物理意义的表达，这一类的研究非常多，如Erberik等[16]对在地中海沿岸地区流行的多层板式混凝土结构的地震易损性和地震损失成本进行了分析，研究中采用了与当地规范反应谱拟合的一组随机人工地震波，结构样本考虑到了若干随机特性，研究初步认为该类结构的地震损失接近常规框架结构，研究采用的就是基于层间变形角的限值损伤指标值；Lamprou等[17]对基于随机地面运动模型的结构全生命周期地震损失进行了研究，文中采用了非线性动力时程法来分析结构性和非结构性构件的损伤和维修成本；唐玉等[18]也以常规的层间位移角的损伤限值状态指标值，将结构分为五个限值水平，基于抗震设计规范(GB50011-2010)分析了结构的地震易损性，并以成本最优化为原则提出了简化的结构全寿命周期地震成本模型；还有Wen、Ramirez、Liu、Fragiadakis、Wang、Taflanidis、Kiureghian、Elnashai、Dong-Woo Seo、Kevin Wong、Chien-Kuo Chiu、Cardone、朱等[19-29]也对诸如钢结构、核电厂房、桥梁等进行了此类研究，上述研究均有一个重要的特点在于选取的结构损伤变形限值状态参数值的精度均在结构整体或结构层变形这一级别，没有分辨层内不同构件的损伤差异和维修成本差异，因此只能对结构地震损失成本进行粗略的估算，无法深入到结构构件级别来对建筑结构的易损性和地震成本进行细致地“刻画”，因为无法精确估算出结构的地震损失成本。经济上的成本无法计算准确，直接影响到业主的工程投资决策、设计方案比选优化、施工-维护成本收益比及最重要的建筑地震保险费率等后续一系列至关重要问题的解决。随着基于性能的工程设计原则的推广和发展，基于组合的地震易损性分析方法近两年引起学术界的关注与应用，被用于研究工程结构全寿命期地震损失成本的评估中，成为目前结构工程和地震工程领域的一个新的研究热点。该方法最初由Porter等[30-31]首次提出，该方法在结构易损性分析思路上与以往分析方法的关键区别之处在于通过精细化模型和对模型构件的分类易损性定义，基于概率评估房屋构件的抗震损伤性能水平，采用基于组合的易损性方程来直接分析工程结构中每一个结构性和非结构性构件的损伤水平，将地震损伤研究的精细化程度从层结构级别进一步细化至结构构件级别，这无疑将工程结构的地震损伤分析研究朝实用化和精确化程度向前大大进了一步，从而推动工程全寿命期地震损失成本研究实现了质的跃升。Christine等[32]遵循PBEE的原则基于IBC2003规范对一栋benchmark标准设计的四层钢筋混凝土框架结构的预期年地震损失成本进行了开创性的分析研究，研究重点构建了两种不同割线刚度的塑性铰单元数字结构模型，采用Pushover推覆法评估了模型的基底剪力-顶层位移性能，采用非线性时程法对比分析了结构的倒塌机理和不同倒塌类型并进一步评估了结构的年平均地震损失成本值，考虑到不同反应谱形的随机地震波在强震情况下对结构地震损伤的影响差异，通过引入谱加速度折减参数ε有效消除了以往在强震分析中对结构倒塌损失进行数字模拟可能导致的高估误差情况，研究中最大的亮点在于该研究继承了基于组合的易损性思想方法，如对结构进行了粗略地细化分类，将结构分为了梁、柱、墙板、油漆粉刷、玻璃、天花板、洒水灭火系统，对于不同的构件采用不同损伤限值状态参数评价指标，对于构件在地震中的损失成本的计算也考虑到了直接维修恢复费用和间接损失费用，具有一定开创性意义；

地震成本损失分析是在前面几步的基础上基于概率法则来进行分析计算的。对于具体的工程结构体系和外加地震激励来说，工程结构体系地震损伤成本相关的性能指标可以表示为h(θ)，该指标与下列因素相关：①基于结构响应计算地震损失； ②假定的地震发生率；③将未来的预期损失值通过折现率i转换为损失现值，即P=F×(1+i)-n，这属于工程经济学中的一部分内容。

预期的全寿命周期地震成本就可以通过简化概率积分方程表示为

C=∫θh(θ)p(θ)dθ

(1)

这里θ可看作风险因子，它主要包括地震本身的不确定性、工程结构抗力性能的不确定性以及随机概率性能评估结果的不确定性。这三方面因素汇总在一起最后就表现为由于地震导致的工程全寿命周期损失成本的风险性，可以用概率模型p(θ)表示，见图1。从方程(1)可知，工程结构全寿命期成本是与结构系统受地震激励响应的性能水平和对应概率的随机积分形式相关，而为了准确评估结构体系中不同构件的地震损失成本，研究中需要将结构的性能水平细化到每一个构件hk(θ)。

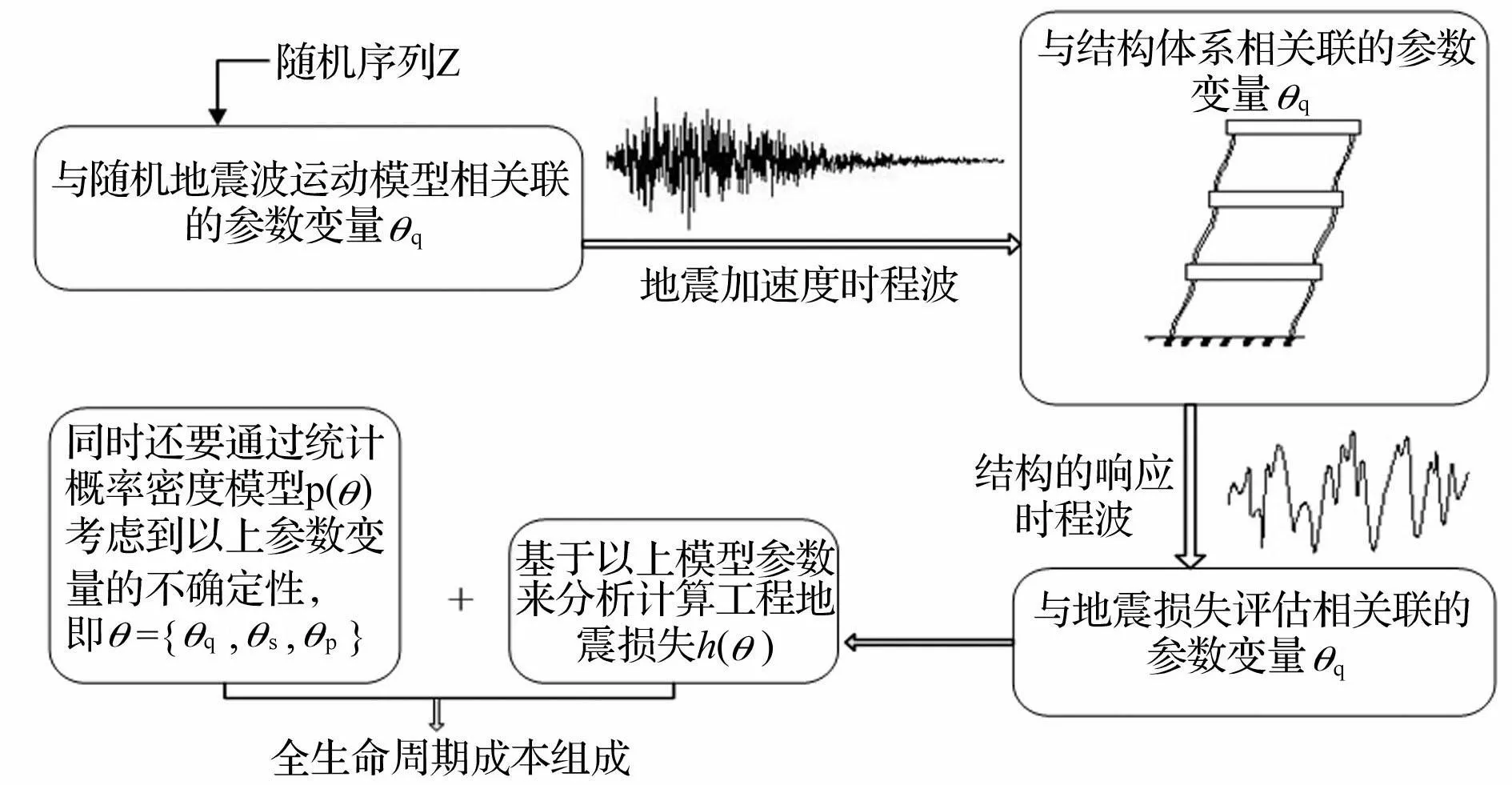
图1　工程结构体系全寿命周期成本相关风险变量来源 Fig.1 Augmented system description for life-cycle seismic cost estimation

工程全寿命期地震损失成本研究实际上是人类对工程结构进行研究和反思后所经历的一个逐步渐进的思想脉络发展过程后的必然结果，最初的工程研究是对结构的某一个部件进行单纯的静力加载分析，进一步发展到构件的动力加载分析，然后是各种类型结构的静力加载分析和动力加载振动台分析，基于概率的结构体系易损性分析，到这一步仍然是工程技术分析，进一步发展就过渡到基于随机概率的结构构件体系的动力损失分析，然后到基于随机概率的结构构件体系全寿命期动力损失成本分析研究，就转变为一个成熟的技术经济综合分析研究，因此当我们回顾这项研究的发展历程会发现，它经历了一个从纯工程技术研究到工程技术应用，再到经济成本核算的实践过程，即这项技术在朝着越来越实用化的方向逐步推进。

2基于组合的地震易损性方法

目前影响最广泛的地震损伤评估方法体系如ATC40和HAZUS系列[33]，它们在实际应用中都存在如下问题，首先这类体系主要还是涉及国外常规类型的典型房屋结构，一般通过Pushover静态推覆法评估结构抗侧力体系，以预先给出它们的性能水平即各级损伤限值状态(参考中位值)，一般分为四级：轻度损伤、中度损伤、严重损伤和倒塌，同时以结构整体或层间的变形作为损伤的指标来研究结构的损伤性能水平，因此该类方法无法实际应用到如核电站厂房、高层或超高层结构、大跨桥梁、大型体育场馆、历史文化建筑物等重要的单体或典型建筑物的全寿命期地震损失评估中；同时HAZUS系列手册是以美国的建筑规范标准来计算统计制订的[34]，如一层的轻钢框架结构房屋规定的典型结构高度约为4.572 m，各国情况不尽相同。因此上述方法在实际应用中也受到了很大的局限，基于此，20世纪80年代初就有学者意识到了这个问题，Scholl[35]提出了一种针对高层特定建筑的地震损伤评估的新策略；Kustu[36]进一步发展了这一基于细部构件的损伤评估策略，即通过探测在结构动力响应中的最大层间位移和最大层间加速度值，将结构响应代入到构件损伤方程中，建立结构响应与典型构件损伤状态值之间的关系，由此可以基于层来进一步了解到房屋构件的损伤状态。但这些早期的方法仍然是采用以往将整个结构简化为单自由度结构、集成层为结点的近似方法，这显然无法区分同一层结构中不同结构构件以及构件加固前后的地震响应差异，但这些分析方法已经在遵守随机统计概率的原则，通过考虑对应于每一级损伤状态的地震损失成本的统计平均值，研究者就可以基于该建筑物的所有构件目录来汇总计算出总的地震损失成本值。这仍然开创了基于组合的地震易损性的崭新方法的序幕。

基于组合的地震易损性方法最早始于核电站厂房的概率风险评估中，该方法主要的计算思路如下：

(1)首先确定建筑物所在的地点、场地条件、建筑结构的全部细节：包括结构性的和非结构性的部分；

(2)选择或创建合适的随机地震加速度时程波作为外在激励；

(3)对结构进行动力时程分析，提取最大响应数据，各类不同的结构响应参数值尽可能都记录，如最大层间加速度、最大瞬间位移、最大塑性铰转角等；

(4)对于建筑中的每一个构件，可选择一个或几个合适的响应参数指标作为评价构件易损性的指标，基于概率确定构件的每一级损伤限值，以此作为其维修或更换的依据；

(5)采用基于单位成本的概率分布计算构件的维修费用，单位成本这部分内容可以考虑参考概预算定额中的相应施工内容的分项工程项目预算价来确定，同时也可以基于定额中分项内容消耗的工日来考虑适当的由于维修导致的时间损失，模拟计算出在不同损伤级别下每一个损伤构件直接维修费用和间接时间损失后，汇总就得到总的维修成本。

以上五步包含了从外加振动、结构响应、损伤分析、维修模拟计算和成本损失核定的一次完整全过程，为了建立基于概率分布的地震易损性方程，需要对以上计算流程重复计算若干次，地震时程波的强度也要同时服从我国建筑抗震规范中规定的大中小地震的不同超越概率，因此上述计算中涵盖了大中小不同强度级别的地震，基于组合的地震易损性计算流程见图2。

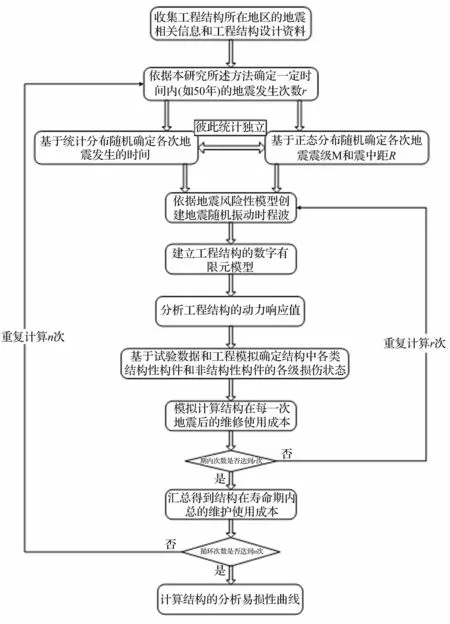
图2　基于组合的地震易损性计算流程 Fig.2 Framework of seismic vulnerability based assemblies

这里r为在工程结构全寿命期内地震发生的次数，每计算r次后就得到一个结构全寿命期内的总维护成本样本值，为了得到寿命期内总维护使用成本的统计期望值，就需用基于随机概率重复计算n次，这里n为研究者依据具体工程结构的规模、复杂程度、计算硬件条件、业主对结果的要求等来确定，循环次数n一般在100～1 000之间。

3工程结构全寿命周期地震成本估算

工程结构的全寿命期地震成本分为直接成本和间接成本，直接成本就是由于地震所导致的房屋构件损坏及维修更换费用，间接成本考虑的是由于构件损坏及维修导致受影响的房屋不能发挥应有的功能而产生的时间收益损失，这部分费用一般以受影响房屋的时间跨度乘以单位时间的收益(如租金)之积来考虑。

设Cj,d为将第j种类型构件从d级损伤状态恢复到无损状态的单位构件直接维修费用，它反映的是业主投入构件维修中各道工序所需的材料、设备、人工费用、施工管理费用及利润，单位维修成本C可假定为一随机变量，其累计概率分布可表示为FCj,d(c)，我们可以将工程结构中处于各个损伤级别的损伤构件的直接维修成本分别进行汇总。

同样建立一个服从标准正态(0，1)分布的样本u，单位维修成本变量C也可表示为其累计概率分布的反函数形式，那么工程结构总的直接维修成本就可以写为单位构件维修成本变量乘以损伤单位构件的数量：

(2)

注意式(2)的直接维修成本并没有对应于具体每个构件的成本数值，而是把它们统一核算为单位构件成本变量Cj,d，这里Nj,d指的是具体构件折算为单位构件的数量，这样做的好处在于简化了计算的过程，提高了计算的效率。

地震后建筑结构产生损伤，依据受损的严重程度，需要时间对受损房屋进行局部或整体的维修，对于重要的公共建筑工程、基础设施等暂时中止服务带来的收益额的减少有时是巨大的，需要单独进行计算，并将其计入间接维修成本是合理的。

通常这部分计算重点考虑房屋结构中的功能性单元构件，如结构性构件、重要的建筑性非承重构件、设备类构件、电力电线系统构件和暖通管道系统构件。

对于间接成本的估算，可以采用工程项目管理中常用的横道图(又名甘特图)来进行计算[37]，在横道图中每一项维修工作用一根横向粗线表示，工作时间的长短用线的长短来表示，每项维修工作的强度或投入资源强度就可以按天来核算，图下方一般还可以汇总出时标维修工作强度或各类资源如投入人工的强度等，各项工作之间的前后逻辑关系使用竖线予以标识，这样整体工程结构的维修工作的总持续时间就可以计算出来，各项工作之间逻辑清晰，工作持续时间显示一目了然，具体施工过程中的工艺参数、空间参数、时间参数包括流水节拍、步距、间歇时间、搭接时间等根据具体工作内容都可以规划和体现。

最后就是维修工作的持续时间具体计算，定义单位构件维修持时Uj,d为专业工人将第j种类型单位构件从d级损伤状态恢复到无损状态所需的工日数，Uj,d就可设为一随机变量，其累计概率分布可表示为FUj,d(ν)，这里ν就是单位构件维修持时Uj,d的具体值。

于是所有在第d级损伤状态的第j类型单位构件进行第m道工序维修作业的总持续时间可以用下式表示

(3)

式中：Rj,d,m就是进行该道工序的总工日数，Nj,d,m为单位构件数量，Uj,d为将第j类型单位构件从第d级损伤状态恢复为无损状态所需要的时间，w为一个工作日每天工作的时间，我国规定为8小时/工日，Ej为第j类型构件该项作业可使用的工人数量。最后计算出来的Rj,d,m单位为工日。

再通过下式进一步计算出第m道维修工序的总的时间：

(4)

式中：RT表示维修工序完成后到可正常使用之间的间隔时间，RT0,m为第m道维修工序开始延误的时间，最后总的维修时间产生的收益损失为：

(5)

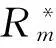
全部的建筑维修成本就是由直接维修成本和间接维修成本组成，即总维修成本

C=CR+CU

(6)

每循环一次就可以得到一个C值，如图2循环计算n次就得到C的一组统计样本值，从中就可以得到总成本的平均值，中位值、标准偏差和数据的统计分布，因此建筑结构在全寿命期内的地震维护成本估算是基于概率的未来合理统计期望值。由以上分析可知，基于组合的地震易损性方法首先可以对重要的城市单体建筑结构(如地标性建筑、核电站厂房、体育馆、医院及其它基础设施等)进行评价，其次对非结构性构件如建筑装饰性构件、水暖管道、电力设备等也可以评价，对于维护成本的每一部分组成也是清晰明了的，设计人员和工程管理人员可以据此进行维护措施的经济损益性分析，调整优化全寿命期内地震维护加固策略，该方法由于其基础性，故应用范围非常广泛，这是基于组合的地震易损性分析方法有别于其他易损性方法的核心差异之处。

4国内外工程全寿命期地震损失成本研究现状及面临的挑战

以往我国对于地震、飓风、海啸等自然灾害对工程项目的影响研究普遍集中在自然灾害作用于结构的受力性能研究上，这属于预防性和工程技术性层面的研究，如研究结构在各种地震或强风荷载瞬时动力作用下的力学性能和损伤性能、各类隔减震及消能加固措施等，对于结构在全寿命期这样一个较长时间跨度内的地震损失成本的研究，因为它需要整合考虑评估工程结构在全寿命期内所受地震灾害的频度、强度、场地条件、基于性能的损伤程度、概率统计模型、维护加固成本算法等多方面因素，这显然比单纯分析构件或结构的动力性能要复杂得多，其意义在于将工程整体防灾减灾研究朝着实用性的目标向前大大的推进了一步，也为将来制订切实可行的地震灾害保险政策奠定基础，因此成为目前防震减灾研究的热点领域。

国内近两年才刚刚开始有学者开展这方面研究，金伟良等[38]对我国目前的工程耐久性和全寿命周期理论的研究现状进行了分析，指出我国目前在工程全寿命设计理论和方法方面还处于起步阶段，文章列出了未来十年(2011～2020)该领域战略研究的5个重点，就包括：结构全寿命性能研究和结构全寿命经济分析研究，显示出对于该方向的研究国内学界是有共识的。

国内研究未来需要开展的工作较多，我认为由于我国地域广阔，不同地区之间地质水文气候等条件差异较大，且很多大中城市处于地震高烈度地区，因此如何构建有效的包含地震次数、地震震级、震中距等要素在内的不同地区地震危险概率算法模型框架是非常重要的。目前针对地震高烈度地区的地震危险概率算法模型研究倾向于同时考虑近断层强脉冲效应，如何将近断层强脉冲地震波考虑进这一算法框架内需要认真考虑。

全寿命期内研究工程结构的地震维护成本损失，其中在结构分析和损伤分析方面也有几个关键问题目前国内很少涉及，但必须突破的新领域，如结构损伤参数的选择，以往采用层间位移角作为结构损伤参数显然无法满足地震维护成本的计算精度和实际工程的需要；损伤限值的确定，也需要依据具体不同的结构构件类型来分别确定，而不是基于类似HAZUS目录体系来简单选取；因此如何深入不同结构的构件级别来分析研究结构的地震易损性成为目前亟需解决的问题。

工程全寿命周期地震成本研究连接着结构分析和经济分析，如何将经济成本分析与地震易损性分析计算结果很好的结合起来，合理地进行建筑结构构件损伤级别与对应的损失值之间的合理估算，如何将各地的概预算定额更好地引入成本研究中，如何创建完善的结构性和非结构性构件分级目录库检索体系，如何基于地震成本最优化来进行结构的基于性能的维护加固方案的优化，这些都是国内外未来面临的新挑战。

国外对工程结构全寿命周期地震损失成本研究历史较长，如前所述至少可追溯到20世纪70年代，由于美、日等发达国家实施房屋地震保险政策多年，客观上为工程结构全寿命期地震损失成本分析研究提供了坚实的基础和良好的外部应用环境，因此在过去半个世纪里国外对地震易损性和工程全寿命期地震损失成本进行了循序渐进的持续性研究，对于本领域的研究也同样面临着实用化和概率精确化的问题，仍然是处在探索前进中，总体来讲按照本研究的目的可分为两个方向，一个方向侧重于通过正向的技术分析讨论经济成本问题，即主要通过工程结构分析来实现结构的地震成本分析，并进一步探讨实现地震损失成本的最小化、地震保险费率的确定甚至于地震损失导致的社会和自然环境等的成本分析，典型成果如：Ramirez 等[23]对所选取的30栋美国加州地震高烈度地区的办公楼样本采用基于性能的地震工程分析流程计算了概率预期的地震年损失和全周期地震成本损失； Seo等[24]对长跨桥梁基于强风的全生命周期易损性与维护成本进行了分析，统计算法被用于研究不确定性来源的风导致的桥面颤动响应及其损伤，研究中使用到了易损性曲线、易损性面并进一步分析了经济损失；Asprone等[39]对意大利全国的8 088个社区的5种建筑结构类型进行了研究，基于全寿命期概率地震损失估计和地震易损性研究成果，计算了期望的保险费率，对包括保险公司和业主的收益和损失全面衡量后提出了适合当地的保险模型； Costantino等[40]基于社会、经济和环境角度探讨了建筑物由于寿命期内的地震所导致的生态可持续性问题，将地震后建筑物的损伤从社会和环境损失的角度进行了评价，将损失的定义跳出了经济范畴，非常新颖的思路。

另一个方向则侧重于通过逆向的分析来探讨技术性问题，即基于通过工程地震成本分析来返过实现对结构的设计参数和加固维护决策的优化；如： Giorgio等[41]对大桥随时间的性能劣化不确定性过程进行了研究，对年久的建筑物提出了一种新的工程全生命周期检查和维修策略，该策略依据每一次检查的结果和损伤的程度来决定不同的维修方案，通过考虑未来系统的失效率和工程项目全生命周期检查和维修成本最小化来作为检查和维修的最优化方案； Lagaros等[42]则对四榀钢结构和钢-混凝土组合结构样本在地震响应下的不确定性来源参数进行研究，为了达成研究目的采用增量动力时程分析方法对结构样本进行了抗力能力和全寿命周期成本分析；Taflanidis等[43]采用概率模拟的方法基于全寿命周期成本原则对流体粘滞阻尼器设计优化参数进行探讨，使用组合易损性方法随机模拟计算了一栋加固后的三层钢筋混凝土结构样本的全寿命周期地震维护成本期望值，使用考虑全寿命周期成本的优化算法确定阻尼器的设计参数。Grace等[44]对采用碳纤维布加固前后的高速公路在20～40年寿命期内的全周期成本进行了研究，研究中考虑了车辆动荷载因素，基于成本最优化得到了碳纤维布加固方案。

工程结构全寿命期地震损失成本研究是基于性能的全寿命周期设计理论及方法的重要内容，是未来结构设计理论与方法应用发展的方向和趋势，是一种正在孕育和发展中的新的结构成本计算和应用理论与方法，是多学科交叉和综合的实践与应用，相比国外的研究成果，目前我国在基于性能的工程结构全寿命周期地震损失成本方面的研究还刚起步，但鉴于其前沿重要性，未来一段时间这方面要要做大量的基础性研究工作。

5结论

针对当前工程结构全寿命期地震损失成本研究面临的挑战和亟需解决的问题，本文认为以下几个方面需要深入研究：

(1)建立完善和详细的地震危险性概率模型数据库。我国幅员辽阔，各地之间的地震活动性存在明显的差异，由于地震发生的时间、频率和强度等均无法准确预测，因此作为导致工程结构发生损伤的主要的外来动荷载来源，如何基于随机统计概率建立适合本地的地震危险性概率模型数据库是准确完成本研究的重要一步；

(2)地震损伤研究方法的深入探讨。这其中涉及到工程结构的有限元建模方法、结构动力分析方法的选择、对结构构件的分类划分、结构不同损伤参数值的选择，对结构构件损伤性能水平的概率分级界定、工程材料以及工程结构模型试验数据的融合分析，地震灾后房屋损伤数据的勘察统计汇总和专家意见的调查参考，这直接关系到工程结构全寿命期地震损伤研究成果的精确性；

(3)由于工程结构全寿命期地震损失成本研究最终还是要反映为经济问题，因此，如何通过技术与经济的交叉研究，将国外这方面的研究成果借鉴过来，如美国RS means每年都出版有基于建筑结构的构件、附件成本数据手册，它提供了准确的构件成本评估价格供设计人员参考，最新的2014版《构件成本数据手册》和《房屋建造成本数据手册》，分别已经更新至第39版本和72版本，涵盖全美900个地区和加拿大的不同价格指数[45-46]。RS means使用三个层次的细节对建筑结构的构件进行分类：分部和子分部、主分类和线列，其中线列主要涉及与地震损伤和维修有关的特别构件，如一些钢结构框架的节点可能需要单独列出，该手册可以供我们在国内确定构件分类和成本计算时做一个参考，同时结合我国的建筑工程估价表和各地的概预算定额更好地应用于本研究中，因此这部分涉及成本的研究虽然面临挑战但依然是有据可循的。

综上所述，对于我国工程结构全寿命周期地震损失成本模型框架体系基于地震高烈度地区进行全面而系统的样本研究，为未来大范围推广积累理论和实践经验，对于改变目前单纯依靠中央政府的行政性救援模式，完善地震、台风、海啸等自然灾害风险转移和补偿机制，对于将来制订切实可行的地震巨灾保险政策奠定坚实可行的理论基础，对于更好地服务于国民经济和我国的防灾减灾事业具有重大而深远的意义。

参考文献

[1]百度百科. 汶川大地震.网址：http://baike.baidu.com.

Baidu Encyclopedia，Wenchuan Earthquake, Website: http://baike.baidu.com.

[2]百度百科. 东日本大地震. 网址：http://baike.baidu.com.

Baidu Encyclopedia，East Japan Earthquake, Website: http://baike.baidu.com.

[3]人民网, 项俊波.建立巨灾保险制度非常紧迫. 网址：http://finance.people.com.cn/insurance.

Renminwang, Xiangjunbo: it’s urgent time for make up huge disaster insurance, Website: http://finance.people.com.cn.

[4]Porter K A. An overview of PEER’s performance-based earthquake engineering methodology[C]//Proceedings of Ninth International Conference on Applications of Statistics and Probability in Civil Engineering, San Francisco,CA, 2003.

[5]Whitman R V, Reed J W, Hong S T. Earthquake damage probability matrices[C]//Proceedings of the Fifth World Conference on Earthquake Engineering, Rome, Italy, 1973,12: 2531-2540.

[6]ATC. Earthquake Damage Evaluation Data for California Report ATC-13[R]. Applied Technology Council, Redwood City, California, U.S.A,1985.

[7]Lantada N, Pujades L G, Barbat A H. Risk scenarios for barcelona, spain,proceedings of the 13th world conference on earthquake engineering[C]. Vancouver, Canada, Paper No. 423,2004.

[8]Oliveira C S, Mota de Sá F, Ferreira M A. Application of two different vulnerability methodologies to assess seismic scenarios in lisbon, Proceedings of the international conference:250th anniversary of the 1755 Lisbon earthquake[C]. Lisbon, Portugal, Paper No. 37, 2005.

[9]Hiroyuki M, Saburoh M, Kazuo F, et al, Earthquake damage estimation in Metro Manila, Philippines based on seismic performance of buildings evaluated by local experts’ judgments[J]. Soil Dynamics and Earthquake Engineering, 2009,28:764-777.

[10]Martinelli A, Cifani G, Cialone G,et al., Building vulnerability assessment and damage scenarios in Celano (Italy) using a quick survey data-based methodology[J].Soil Dynamics and Earthquake Engineering,2008, 28:875-889.

[11]ATC. Seismic evaluation and retrofit of concrete buildings, report ATC-40, applied technology council[R]. Redwood City, California, U.S.A,1996.

[12]Barbara B, Rui P, Helen C. Simplified Pushover-based vulnerability analysis for large-scale assessment of RC buildings[J], Engineering Structures,2008, 30:804-820.

[13]Rossetto T, Elnashai A. A new analytical procedure for the derivation of displacement-based vulnerability curves for populations of RC structures[J]. Engineer Structures,2005,27: 397-409.

[14]Li G, Jiang Y, Yang D X.Modified modal pushover based seismic optimum design for steel structures considering life-cycle cost[J]. Structural and Multidisciplinary Ptimization,06/2012,45(6):861-874.

[15]Gencturk B. Life-cycle cost assessment of RC and ECC frames using structural optimization[J]. Earthquake Engineering & Structural Dynamics, 2013,42:61-79.

[16]Erberik M A, Elnashai A S. Fragilityanaly sis of flat-slab structures[J]. Engineering Structures, 2004,26: 937-948.

[17]Lamprou A, Jia G, Taflanidis A A. Life-cycle seismic loss estimation and global sensitivity analysis based on stochastic ground motion modeling[J]. Engineering Structures, 2013, 54:192-206.

[18]唐玉,郑七振,楼梦麟. 基于“投资-效益”准则的抗震性能目标优化决策[J].同济大学学报:自然科学版, 2012,40(11):1613-1619.

TANG Yu, ZHEN Qi-zhen,LOU Meng-ling. Optimization of seismic performance objectives based on cost effectiveness criterion[J]. Journal of Tongji University, 2012,40(11):1613-1619.

[19]Wen Y K, Kang Y J. Minimum building life-cycle cost design criteria. II: Applications[J]. Journal of Structural Engineering (ASCE) 2001,127(3):338-346.

[20]Liu M, Burns S A, Wen Y K. Optimal seismic design of steel frame buildings based on life cycle cost considerations[J]. Earthquake Engineering and Structural Dynamics, 2003,32:1313-1332.

[21]Takahashi Y J, Kiureghian A D. Life-cycle cost analysis based on a renewal model of earthquake occurrences[J]. Earthquake Engng Struct. Dyn. 2004,33:859-880.

[22]Fragiadakis M, Lagaros N D, Papadrakakis M. Performance based multi objective optimum design of steel structures considering life-cycle cost[J]. Struct Multidiscip Optimiz, 2006,32:1-11.

[23]Ramirez C M, Ciel A B, Mitrani-Reiser J, et al. Expected earthquake damage and repair costs in reinforced concrete frame buildings [J]. Earthquake Engineering & Structural Dynamics,2012, 41,(11):1455-1475.

[24]Seo D W, Caracoglia L. Estimating life-cycle monetary losses due to wind hazards: Fragility analysis of long-span bridges[J]. Engineering Structures, 2013, 56:1593-1606.

[25]Wong K K F ,Harris J L. Seismic fragility and cost analyses of actively controlled structures[J]. Struct. Design Tall Spec. Build,2013, 22:569-583.

[26]Wang H, Weng D G, Lu X L, et al. Life-cycle cost assessment of seismically base-isolated structures in nuclear power plants[J]. Nuclear Engineering and Design, 2013,262:429-434.

[27]Chiu C K, Hsiao F P, Jean W Y,et al. A novel lifetime cost-benefit analysis method for seismic retrofitting of low-rise reinforced concrete buildings[J]. Structure and Infrastructure Engineering, 2013,9(9):891-902.

[28]朱健.结构动力学原理与地震易损性分析[M].北京：科学出版社，2013.

[29]Cardone D, Flora A. Direct displacement loss assessment of existing RC buildings pre-and post-seismic retrofitting: A case study[J]. Soil Dynamics and Earthquake Engineering,2014,64:38-49.

[30]Porter K A, Kennedy R P, Bachman R E. Creating fragility functions for performance-based earthquake engineering[J]. Earthquake Spectra, 2007,23:471-89.

[31]Porter K A, Kiremidjian A S, LeGrue J S. Assembly-based vulnerability of buildings and its use in performance evaluation[J]. Earthquake Spectra, 2001, 18:291-312.

[32]Christine A G, Curt B H, Judith M R, et al, Evaluation of the seismic performance of a code-conforming reinforced concrete frame building—from seismic hazard to collapse safety and economic losses[J]. Earthquake Engng Struct. Dyn, 2007, 36:1973-1997.

[33]Kirch C A, Whiteman R V, Holmes W T. Hazus earthquake loss estimation methods[S]. Nat Hazards,2006,32:1-11.

[34]Mrl H M, Multi-Hazard loss estimation methodology:Earthquake model[S]. Department of Homeland Security, FEMA, Washington D.C,2003.

[35]Scholl R E. Seismic damage assessment for highrise buildings, open-file report 81-031, US Geological Survey[J]. Menlo Park, CA,1980:143.

[36]Kustu O. Earthquake damage prediction for buildings using component test data[C]. Third U.S. National Conference on Earthquake Engineering, 1986:Aug 28, Charleston, South Carolina, Earthquake Engineering Research Institute, El Cerrito,CA, 2,1493-1504.

[37]田金信.建设项目管理[M].北京：高等教育出版社，2009.

[38]金伟良，牛荻涛.工程结构耐久性与全寿命设计理论[J].工程力学，2011,28(增刊2):31-37.

JIN Wei-liang, NIU Di-tao. The state of the art on durability and life cycle design theory of engineering structures[J]. Engineering Mechanics,2011,28(Sup2):31-37.

[39]Asprone D, Jalayer F,Simonelli S,et al. Seismic insurance model for the Italian residential building stock[J]. Structural Safety, 2013, 44:70-79.

[40]Costantino M. Assessment of ecological sustainability of a building subjected to potential seismic events during its lifetime[J]. Int J Life Cycle Assess, 2013,18:504-515.

[41]Barone G,Frangopol D M, Soliman M, et al. Optimization of life-cycle maintenance of deteriorating bridges with respect to expected annual system failure rate and expected cumulative cost[J]. J. Struct. Eng, 2013,140(2):04013043.

[42]Lagaros N D, Mitropoulou C C. The effect of uncertainties in seismic loss estimation of steel and reinforced concrete composite buildings[J]. Structure and Infrastructure Engineering, 2013, 9(21): 546-556.

[43]Taflanidis A A, Gidaris I.Life-cycle cost based optimal retrofitting of structures by fluid dampers[C]. Structures Congress,2013, ASCE.

[44]Grace N F,Jensen E A, Eamon C D, et al. Life cycle cost analysis of carbon fiber-reinforced polymer reinforced concrete bridges[J].ACI Structural Journal,2012,109(5):697-704.

[45]RS Means Co. Building construction cost data 2014 Book[M]. 72ndAnn.Ed, Kinston, MA, 2014.

[46]RS Means Co. Assemblies cost data 2014[M]. 39thAnn.Ed, Kinston, MA, 2014.