风电叶片两点疲劳加载系统振动耦合特性

第一作者张磊安男，博士，讲师，1982年7月生

风电叶片两点疲劳加载系统振动耦合特性

张磊安1,2,3，黄雪梅1，姚锦恺1

(1. 山东理工大学机械工程学院，山东淄博255091；2.中国矿业大学机电工程学院，江苏徐州221116；3.连云港中复连众复合材料集团有限公司，江苏连云港222000)

摘要：针对风电叶片单点疲劳加载方法驱动能力不足且试验周期较长的问题，设计一种新型两点疲劳加载测试系统。通过对加载系统进行合理简化，建立风电叶片两点疲劳加载振动系统的机电耦合数学模型。利用Matlab/Simulink软件建立加载系统的仿真模型，对加载系统的机电耦合过程进行仿真，得到不同电动机转速、不同初始相位差对加载系统机电耦合过程的基本影响规律。最后搭建了一套小型风电叶片两点疲劳加载试验系统，得到试验结果与仿真结果规律基本吻合，验证了数学模型和仿真模型的准确性。为后续两点疲劳加载试验的精确控制以及叶片的优化设计提供了理论依据。

关键词：风电叶片；机电耦合；数学模型；数值仿真；疲劳加载试验

基金项目：国家自然科学基金(51405275，51305243)；山东省自然科学基金(ZR2014EL027)；中国博士后科学基金(2015M571840)

收稿日期：2015-01-14修改稿收到日期：2015-04-10

中图分类号:TH113

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.17.014

Abstract:Aiming at lack of driving capacity and longer test period of a single-point fatigue loading system, a dual-point fatigue loading system for wind turbine blades was designed. By simplifying the loading system rationally, its electromechanical coupling mathematical model was established, and then its simulation model was built with Matlab/Simulink software. By simulating the electromechanical coupling process of the dual-point fatigue loading system, the basic influence laws of different motor speeds and different initial phases on the electro-mechanical coupling process were obtained. Finally, a small dual-point fatigue loading test system for wind turbine blades was set up. The test results agreed well with the simulation ones. The correctness of the mathematical model and simulation model were validated. The study results provided a theoretical basis for the subsequent precise control of dual-point fatigue loading tests and optimal design of blades.

Vibration coupling features for a dual-point fatigue loading system of wind turbine blades

ZHANGLei-an1,2,3,HUANGXue-mei1,YAOJin-kai1(1. School of Mechanical Engineering, Shandong University of Technology, Zibo 255091, China;2. School of Mechanical and Electrical Engineering, China University of Mining & Technology, Xuzhou 221116, China;3. Lianyungang Zhongfu Lianzhong Composite Group Co.,Ltd, Lianyungang 222000, China)

Key words:wind turbine blade; electromechanical coupling; mathematical model; simulation model; fatigue loading test

风力发电是一种高生态效益和经济效益的可再生能源。根据国际能源署《风能技术路线图》报告，到21世纪中叶风力发电占全球电力供应的比例将由目前的2%上升到12%[1]。在风力发电机组中，叶片是接受风能的最主要部件，大量事故和研究结果表明，由于受交变载荷的影响，疲劳破坏是叶片的最主要的失效方式之一[2-4]。因此对风电叶片进行疲劳性能测试是一种可靠且有效的检测方法。

目前国内外风电叶片疲劳加载试验通常是以沿叶片展向的弯矩为试验依据，振幅和振动次数呈反比关系，加载方法通常采用单点激励(包含：单轴和两轴)进行疲劳性能测试[5]。但是在相同的加载条件下，采用单点激励时叶片的振幅明显小于两点激励，即每个振动周期叶片的能量损耗相对较少，所以单点疲劳加载测试方法存在驱动能力不足且试验周期较长等缺点，因此本文提出采用两点加载方法对风电叶片进行疲劳性能测试。两点疲劳加载试验系统构成了一个非常复杂的非线性机电耦合系统。Blekhman等[6]首先对偏移式振动机的机电耦合特性进行了深入分析，建立了双电机振动耦合动力学模型，开发的振动机械装置也得到了较好的应用。张楠等[7]针对同相回转系统，采用数值仿真和试验验证相结合的手段，可视化地再现了机电耦合特性。王得刚等[8]针对双电机联振的稳定性问题，通过建立机电耦合动力学模型，对振动系统的关键参数进行无量纲化处理，定量分析了两个加载源之间的机电耦合特性。来鑫等[9]建立了对称布置电机驱动的振动沉桩机电耦合数学模型，同时采用bang-bang控制算法，保证了两个电机速度和相位的同步性，取得了较好的实际应用效果。上述研究表明，双电机联动之间的耦合现象是固有存在的，为本课题两点疲劳加载系统的振动耦合机理研究奠定了基础。从目前的文献资料来看，国内外对于风电叶片两点疲劳加载系统振动耦合特性的研究还没有开展。

本文在提出风电叶片两点疲劳加载测试方法的基础上建立了两点疲劳加载系统的机电耦合数学模型和仿真模型，对该系统的振动特性进行数值仿真，最后进行风电叶片两点疲劳加载现场试验，对数学模型和仿真模型进行验证。为后续两点疲劳加载试验的精确控制以及叶片的优化设计提供了理论依据。

1振动系统的机电耦合数学模型

1.1风电叶片两点疲劳加载系统数学模型

风电叶片两点疲劳加载测试系统由加载基座、风电叶片、疲劳加载系统等构成，其中疲劳加载系统由偏心块、变频电动机、夹具、减速箱和电控系统等组成，其示意图见图1。加载基座固定在地面上，通过若干个高强度螺栓将风电叶片的根部固定在加载基座上，两个加载源布置在沿叶片展向位置上。

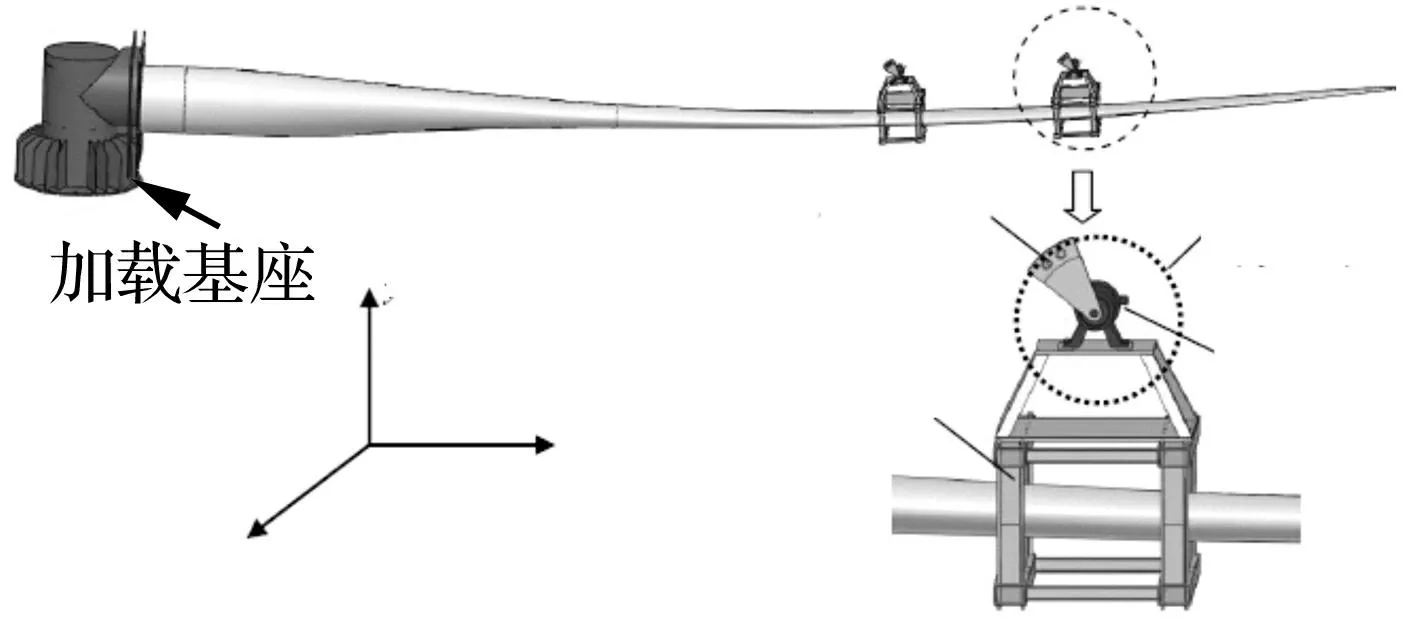
图1　风电叶片两点疲劳加载系统 Fig.1 Dual-point fatigue loading system of wind turbine blade

两点疲劳加载测试系统的动力学模型见图2。在建立该模型时，为了简化系统，假设叶片在各个方向上受到的阻尼力和弹性力分别是该方向上速度和位移的线性函数。

图2　风电叶片两点疲劳加载振动系统动力学模型 Fig.2 Dynamic model of dual-point fatigue loading system of wind turbine blade

按照拉格朗日方程法[10]，以x、y、z、φi、θi(i=1,2)为广义坐标，建立该振动系统的动力学方程：

(1)

式中：φi为oxyz分别与两动坐标系之间的夹角(i=1,2)；li1为ooi在yoz坐标平面内的投影，li2为ooi在xoy平面内的投影(i=1,2)；l01、l02为oo‴在yoz和xoy坐标平面内的投影；βi1为li1与z轴正方向夹角，βi2为li2与x轴正方向夹角，β0i为l0i与y轴负方向的夹角；kx、ky、kz、kφi为x、y、z、φi方向上叶片刚度系数；cx、cy、cz、cφi为x、y、z、φi方向上的阻尼系数；Joi为系统绕x、z轴转动的转动惯量；Ji为电动机i的转动惯量；Tmi为电动机i转轴上的电磁转矩(i=1,2)。

1.2三相异步电动机的数学模型

本文中风电叶片两疲劳加载系统均是通过一个变频电动机带动偏心块回转产生激振力对叶片进行疲劳加载的，建立基于αβ0系统下的电动机数学模型[11]。

电动机三相静止绕组A、B、C和两相静止绕组的变换方程为：

(2)

电动机的电压方程为：

(3)

在αβ0系统下，电动机的磁链方程为：

(4)

电磁转矩及转矩方程为：

Te=npLm(iβ1iα2-iβ2iα1)

(5)

(6)

式中 ：R1、R2为定、转子绕组电阻；iα1、iβ1为αβ0系统下定子端电流；iα2、iβ2为αβ0系统下转子端电流；uα1、uβ1为αβ0系统下定子端电压；uα2、uβ2为αβ0系统下转子端电压；ωr为转子转动角速度；ψα1、ψβ1为αβ0系统下定子磁链；ψα2、ψβ2为αβ0系统下转子磁链；Ls、Lr为定、转子绕组自感；Lm为定、转子绕组互感；Te为电动机电磁转矩；TL为负载转矩；np为电动机磁极对数；J为电动机转动惯量；p为微分算子。

方程(1)～(6)构成了风电叶片两点疲劳加载系统的机电耦合数学模型，该数学模型是一个非理想空间耦合模型，描述了加载过程中动力系统和振动系统之间的空间耦合效应。从该数学模型可以看出，影响振动耦合的因素有两偏心块初始相位差、转速和异步电动机机械特性等。

2加载系统耦合过程仿真分析

采用Matlab/simulink软件对电动机转速和初始相位差对系统耦合过程的影响规律进行仿真，仿真参数设置为：m=29 kg，m1=m2=2 kg，r=0.15 m，l01=0.05 m，l02=0.25 m，l11=l21=0.13 m，l12=l22=0.32 m，k=126 N/m，叶片阻尼近似取0.025，电机功率P=0.75 kW，β01=45°，β02=2.5°，β11=42°，β12=160°，β21=138°，β22=20°。

当两偏心块初始相位差为π/2，转速分别设置为150 r/min，180 r/min，210 r/min，230 r/min，260 r/min时的仿真结果见图3。

图3　不同电机转速时相位差仿真曲线 Fig.3 Phase difference simulation curve of different motor speed

由图3可知，在不同转速下，两偏心块相位差会逐渐收敛于零。且当电动机的转速为260 r/min时，相位差收敛于零的速度最快约40 s，随着转速的减小，相位差收敛于零的速度也随之减慢。当转速减到150 r/min时，相位差收敛于零的用时已超过100 s。当电动机转速为260 r/min时，y方向上的振幅仿真曲线见图4。

图4　y方向振幅变化仿真曲线 Fig.4 Blade amplitude variable simulation curve of y axis

从上图得出，在相位差逐渐趋向于零的过程中，发生了回转频率俘获现象，两个电机的振动步调也趋于一致。在初始相位差一定的前提下，电动机速度越大，发生频率俘获现象的速度越快。当电动机转速为260 r/min时，经过40 s就发生了频率俘获现象，此时叶片振幅也趋于稳定振动状态(见图4)。

将两电机的转速均设定为230 r/min，两偏心块初始相位差分别为-5π/6，-π/2，-π/6，π/6，π/2，5π/6和π时的仿真结果见图5。

图5　不同初始相位差时相位差仿真曲线 Fig.5 Phase difference simulation curve of different initial phase

由图5可知，在相同转速和较小的初始相位差前提下，两偏心块相位差在一定时间内会逐渐收敛于零，也发生频率俘获现象。初始相位差越大，发生频率俘获现象越慢。当两电机初始相位差为π时，相较于其它情况，相位差需要经过较长的时间才能收敛于零，此时系统很难达到同步状态。若要得到较稳定的振幅，应避免两电机初始相位差为π的情况。

将两电机转速分别设置为230 r/min和217 r/min时，相位差仿真结果见图6，y方向振幅仿真结果见图7。

图6　两电机转速不同时相位差仿真曲线 Fig.6 Phase difference simulation curve under the two motor with different speed

图7　两电机转速不同时y方向振幅变化仿真曲线 Fig.7 Blade amplitude variable simulation curve of y axis under the two motor with different speed

由上图可知，在较大的初始转速下，两偏心块的相位差越来越大，两个加载系统不能自动到达同步振动状态，y方向上的振幅也不能达到稳定状态，即不会发生频率俘获现象。因此，要得到较稳定的振幅，两电机的转速要尽可能相同，需要对两个加载源进行解耦同步控制。

3试验验证

为了验证理论分析与仿真结果的正确性，搭建了一套小型风电叶片两点疲劳加载试验系统，试验现场见图8，部分试验参数如表1所示。

表1　试验参数

图8　风电叶片两点疲劳加载试验现场 Fig.8 Dual-point fatigue loading test of wind turbine blade

通过齿轮测速传感器(CORON-CTS)实时采集两加载源的转速和相位，在上位机进行数据存储。y方向上的振幅采用激光测距仪(ADSL-30)进行采集。

试验时设定电机转速均为230 r/min，两偏心块初始相位差为π/6，试验结果见图9和图10。

图9　相位差试验曲线 Fig.9 Phase difference test curve

图10　y方向振幅试验曲线 Fig.10 Blade amplitude variable test curve of y direction

从图10可知，两偏心块的相位差逐渐从π/6收敛于零，同时y方向上的振幅也逐渐趋于稳定振动状态，振幅基本稳定在±0.25 m之间。

两电动机转速分别设定为230 r/min和217 r/min时，试验结果见图11和图12。

图11　两电动机转速不同时的试验结果 Fig.11 Phase difference test curve under the two motor with different speed

图12　两电动机转速不同时，叶片振幅试验曲线 Fig.12 Bladeamplitude curve under two motor with different speed

试验结果得出，当设定的初始转速相差较大时，两偏心块的相位差会越来越大，两个加载系统很难自动达到振动同步状态，叶片振幅表现为絮乱状态，上述试验结论与仿真结果基本一致。

4结论

本文通过对风电叶片两点疲劳加载系统振动特性进行研究，得到以下结论：

(1)通过建立风电叶片两点疲劳加载振动系统的机电耦合数学模型，发现影响系统机电耦合特性的主要因素有疲劳加载系统两偏心块初始相位差、转速和偏心矩、加载系统的安装位置、异步电动机机械特性、风电叶片质量和重心等。

(2)通过建立仿真模型，可视化地得到振动系统的耦合特性。当两偏心块存在初始相位差时，由于耦合作用的存在，相位差会逐渐收敛于零，即发生了频率俘获现象，此时叶片会有较稳定的振幅，且电机转速越快，相位差收敛于零的速度就越快。

(3)当两电机初始转速相同时，即使存在较小的初始相位差，系统也能够逐渐处于同步振动状态，即发生频率俘获现象，且初始相位差越大，发生频率俘获的过渡时间越长。

(4)通过进行现场试验，得到了与仿真分析同样的结论，验证了本文构建的数学模型的正确性。

参考文献

[1]Court R S, Ridley S, Jones H, et al. Fatigue testing of wind turbine blades with computational verification[J]. ICCM-17, Edinburgh, 2009.

[2]Kong C, Bang J, Sugiyama Y. Structural investigation of composite wind turbine blade considering various load cases and fatigue Life[J]. Energy, 2005, 30:2101-2114.

[3]White D, Musial W, Engberg S. Evaluation of the NEW B-REX fatigue testing system for multi-megawatt wind turbine blades[J]. 43rd AIAA Aerospace Sciences Meeting and Exhibit, USA, 2005, 6:10-13.

[4]李树虎,王丹勇,秦贞明,等.纤维增强复合材料风力发电机叶片性能检测综述[J].工程塑料应用,2010,38(9):54-58.

LI Shu-hu,WANG Dan-yong, QIN Zhen-ming,et al. Sumary of property testing for composites wind turbine blade[J]. Engineering Plastics Application, 2010, 38(9):54-58.

[5]Puneet M. Advanced blade testing methods for wind turbines[D].University of Massachusetts Amherst,2010,9:12-32.

[6]Blekhman I I,Fradkov A L,Tomchina O P. Self-synchronization and controlled synchronization: general definition and example design[J]. Mathematics and Computers in Simulation, 2002, 58(4-6):367-384.

[7]张楠，侯晓林，闻邦椿.机电耦合情况下振动机的同相同步特性 [J].东北大学学报:自然科学版， 2009, 30(10): 1477-1480.

ZHANG Nan, HOU Xiao-lin, WEN Bang-chun. Cophase and synchronous characteristic of vibration machine under electromechanical coupling condition[J].Journal of Northeastern University:Natural Science Edition, 2009,30(10):1477-1480.

[8]王得刚，姚庆良，冯霏，等.自同步振动系统的动力学耦合特性及试验[J]. 振动、测试与诊断，2012, 32(增刊2): 53-58.

WANG De-gang, YAO Qin-liang, FENG Fei, et al. Dynamic coupling feature and experimental study of self-synchronous vibrating system[J].Journal of Vibration, Measurement Diagnosis, 2012,32(Sup2): 53-58.

[9]来鑫，乌建中，张珍,等. 多桩锤同步振动系统及同步控制策略研究 [J].振动与冲击，2012,31(3): 147-152.

LAI Xin, WU Jian-zhong, ZHANG Zhen,et al. Synchronous vibration system of multi-hammer and synchronous control strategy[J], Journal of Vibration and Shock,2012, 31(3):147-152.

[10]闻邦椿,刘树英,陈照波,等.机械振动理论及应用[M]. 北京:高等教育出版社,2009.

[11]李岚，杨冠路，孙学政.无刷绕线型异步电动机的数学模型及稳态特性分析[J].电工技术学报，2001,16(5):16-19.

LI Lan, YANG Guan-lu，SUN Xue-zheng. Mathematical model and steady state characteristics of brushless wire-wound asynchronous motor[J]. Transactions of China Electrotechnical Society,2001,16(5):16-19.