耦合四圆柱涡激振动的力特性及水动能获取分析

第一作者罗竹梅女，博士生，副教授，1979年1月生

通信作者张立翔男，教授，1959年生

耦合四圆柱涡激振动的力特性及水动能获取分析

罗竹梅1，张立翔2

(1. 昆明理工大学能源与动力工程系，昆明650093； 2. 昆明理工大学工程力学系，昆明650051)

摘要：涡激振动是一种常见的流固耦合现象，结构物振幅较大时，可利用涡激振动从海洋流中或河流中获取能量。通过流固双向耦合数值方法，模拟均匀来流下，弹性支撑刚性连接的耦合四圆柱在不同横向和流向间距比下的横向涡激振动。分析横向和流向间距比对该耦合结构涡激振动时的压力和升力特性及获取能量和能量密度的影响。结果表明：各种组合间距比下，上端两圆柱的升力系数均值CL与下端两圆柱的CL关于CL=0对称，压力系数幅值Ap关于θ =180°对称，但其升力系数均方根值却近似相等；获取的水动能及能量密度随着组合间距比的增加先增加，随后获取能量增加缓慢，而能量密度却不断减少，因此选择合理的横向和流向间距比可从单位水体的海洋流或河流中获取更多的水动能。

关键词：流固双向耦合；耦合圆柱；涡激振动；间距比；能量密度

基金项目：国家自然科学基金项目(51279071，51309128);云南省教育厅基金项目(2012Y546)

收稿日期：2014-08-01修改稿收到日期：2014-09-25

中图分类号:TK79；TK730.2

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.17.005

Abstract:Vortex-induced vibration (VIV) is a common phenomenon of fluid-structure interaction. When VIV of a structure in water is larger, it can be used to extract energy from ocean or river currents. Here, a numerical method using two-way coupling between fluid and structure was presented to simulate VIV of four coupling-linked and spring-mounted cylinders in uniform currents. Different stream-wise and transverse spacing ratios were applied in simulation to identify their influence on not only lift and pressure characteristics but also energy harvesting and power density. The results revealed that the mean lift force coefficient CL of upper two cylinders and that of lower two cylinders are symmetrical about CL=0, the amplitudes of pressure coefficients are also symmetrical about θ=180° under various combinations of spacing ratios; the root mean square of lift force coefficient of upper two cylinders is approximately equal to that of lower two cylinders; the energy harvesting and power density increase with increase in spacing ratios firstly, then the energy harvesting increases slowly while the power density decreases; so reasonable stream-wise and transverse spacing ratios should be chosen to extract more hydrokinetic energy from water currents.

Force characteristics and hydrokinetic energy harvesting for VIV of four coupling-linked cylinders

LUOZhu-mei1，ZHANGLi-xiang2(1．Department of Energy and Power Engineering，Kunming University of Science and Technology，Kunming 650093，China;2．Department of Engineering Mechanics，Kunming University of Science and Technology，Kunming 650051，China)

Key words:fluid-structure two-way coupling; coupling-linked cylinders; vortex-induced vibration (VIV); spacing ratio; power density

流体流过多个圆柱体组成的圆柱群是工程中的一种常见现象，例如架空电缆线、近海平台、热交换器中管阵系统等。流体流过圆柱群时，尾涡脱落引发结构振动，这种涡激振动长期作用引起结构疲劳，降低结构寿命。一直以来，这一问题都成为工程师和研究人员的研究重点。然而，近年来Bernitsas等[1-4]对涡激振动的研究不是基于抑制涡激振动，而是增强涡激振动：仅研究了由单个圆柱组成的能量转换器利用涡激振动从海洋流或河流中获取水动能，并将获取的水动能转换成电能。均匀来流下，弹性支撑的刚性圆柱在较广的流速和雷诺数范围内，都能产生有效振动，即使在低速海洋流或河流中也可获得较大横向水动能。这一想法对于可再生海流能和河流能的利用具有重要意义。

事实上，若要大规模利用低速海洋流或河流中的水动能，能量转换器应由大量圆柱组成，且圆柱间刚性连接，各圆柱位置相对不变。作为圆柱群基本组成单元的四圆柱，很少有学者对其涡激振动进行研究[5-6]，一般都集中在低雷诺数下的多柱体固定绕流或对海洋柔性管的涡激振动研究[7]。徐枫[8]对正三角形布置三圆柱绕流及涡致振动进行数值模拟，该三圆柱非耦合刚性连接系统，各圆柱为独立弹性支撑的刚性圆柱。Lam等[9]和Zou等[10]用数值方法分别模拟了正方形布置和菱形布置的四圆柱在雷诺数Re=200时的绕流情况，并分析间距比对水动力的影响。Zhao等[11]对间距比不变的正方形四圆柱在不同来流入射角时的涡激振动进行了模拟。对弹性支撑的耦合四圆柱系统其涡激振动及水动能获取的研究还未见文献报道，该圆柱系统中各圆柱为低质量比的刚性体，且圆柱间相对位置不变。此外横向间距比和流向间距比影响结构的涡激振动响应和水动力特性，从而影响其从海洋流或河流中获取的水动能。本文采用流固双向耦合数值方法，模拟不同横向和流向间距比下，弹性支撑的耦合四圆柱在不同均匀来流条件下的涡激振动，并分析其涡激振动时的升力和压力特性及间距比对水动能获取和能量密度的影响。

1数值计算方法

1.1流体控制方程

流体控制方程采用二维不可压缩雷诺平均Navier-Stokes(RANS)方程和连续方程。由于流固耦合边界随时间不断变化，考虑网格移动速度，流体控制方程的无量纲形式可写为：

(1)

(2)

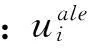
(3)

用有限体积法离散流体控制方程。由于k-ω模型能较好预测逆压梯度下壁面边界分离流动的产生和发展，k-ε模型能较好地模拟远离壁面充分发展的湍流，因此采用在Wilcox基础之上Menter发展的SST(Shear-Stress Transport)k-ω湍流模型封闭上述方程中的湍动能k和湍流粘度νt。该模型集合了k-ω模型和k-ε模型的优点。

1.2结构控制方程

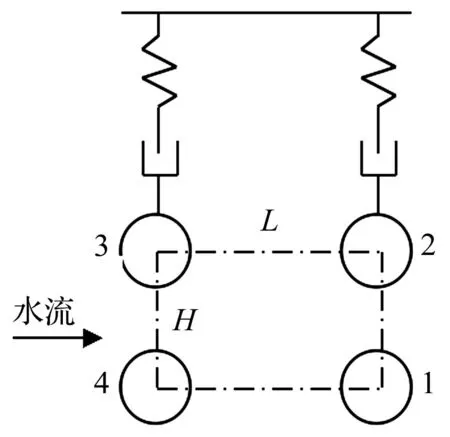
图1　耦合连接矩形 布置的四圆柱系统模型 Fig.1 The model of four coupling linked cylinders with rectangular arrangement

弹性支撑的耦合四圆柱系统简化为见图1的质量-弹簧-阻尼系统。圆柱间呈矩形布置，流向间距为L，横向间距为H。3、4圆柱位于上游，1、2圆柱位于下游。

结构控制方程采用有限元数值离散方法，矩阵形式为：

(4)

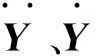
用增量有限元的形式对式(4)进行逐步隐式时间积分：

(5)

用式(6)进行平衡迭代计算：

(6)

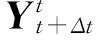
通过流固耦合求解器将离散后的流体和结构模型同时进行求解，此时流体和固体的求解变量完全耦合[12]。耦合边界上应用位移协调条件、力平衡条件以及速度平衡条件，可实现流体和结构双向耦合计算，模拟真实的涡激振动现象。

2数值实验方案

论文采用三个可产生较大横向振幅的约化速度Ur(Ur=U/fn,wD，U为均匀来流速度，fn,w为圆柱系统在水中的固有频率，通过改变流速改变约化速度)，Ur分别取6、7、8。对表1的12种组合间距比方案进行涡激振动模拟计算。结构质量比m*=2(m*为振动体质量与排开流体质量之比)，阻尼比ζ=0.05，质量阻尼比m*ζ=0.1，单个圆柱直径D=0.1m。

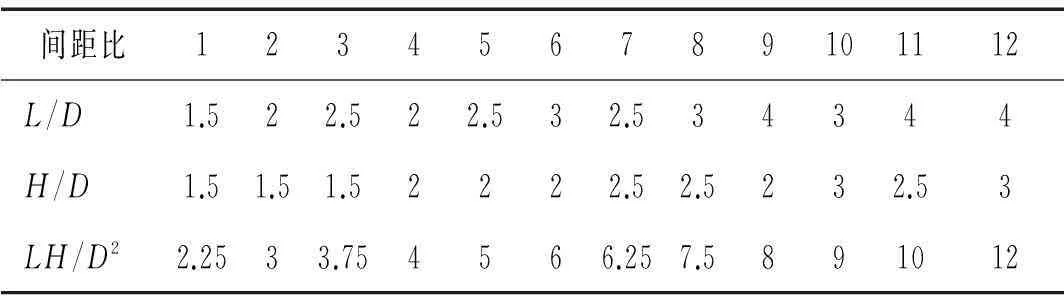
表1　间距比方案

3结果分析

3.1升力特性

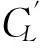
图2(a)、2(b)和2(c)为三个约化速度下各圆柱的升力系数均值CL。由图可知：由于圆柱3在流线方向与圆柱4呈对称布置，各种间距比和约化速度下，圆柱3的CL值与圆柱4的CL值关于CL=0对称，同样的结果也出现在流线方向呈对称布置的圆柱2和圆柱1上。无论耦合圆柱系统在哪个约化速度下振动，小间距比时，上游圆柱3、4的自由剪切层包围或重附在下游圆柱1、2上；大间距比时，虽然上端两圆柱2、3与下端两圆柱1、2间水流的横向作用较小，但上游圆柱形成的脱落涡冲击着下游圆柱，因此下游圆柱1、2的CL值较小，接近0，明显小于上游圆柱3、4的CL值。当L/D=1.5，H/D=1.5时，圆柱3、4的CL其绝对值最大，这说明与小间距比的固定四圆柱绕流一样，耦合四圆柱振动时，圆柱间存在较高流速的射流。但当LH/D2≥4时，随着横向和流向间距的逐渐增加，圆柱间流体的相互作用减弱，使得CL值逐渐减少。从图中还可以看出，在相同的横向和流向间距比下，随着约化速度的增加，CL没有增加，反而减小。

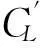
3.2压力特性

由于圆柱间以不变的相对位置同时振动，其表面压力分布及压力系数值也必定不同与固定四圆柱绕流时的情况。为了了解耦合四圆柱在一个周期内各圆柱表面的瞬时压力情况，提取一个周期内5个典型时刻(见图3(a))各圆柱表面的瞬时压力值，并进行瞬时压力系数Cp(Cp(θ)=(p(θ)-p∞)/0.5ρU2)的计算，结果见图4。图中圆柱系统间距比为L/D=4且H/D=2，约化速度Ur=7。当t=55.3s(点1)时圆柱在中心位置开始向上振动，在t=55.52s(点2)时，出现正方向的最大位移，随后向下运动；t=55.74s(点3)时，系统回到中心位置直到t=55.96s(点4)达到负方向最大位移，最后在t=56.18s(点5)时重现回到中心位置，系统开始进入下一个振动周期。当圆柱系统在中心位置(点1，点3和点5)时，上下游各圆柱瞬时压力系数在圆柱表面四周大致呈正弦规律变化。当耦合四圆柱振动趋于稳定后，由于点5即为一个周期的结束时刻，同时也为下一个周期的开始时刻，其运动趋势与点1相似。因此，通过计算后得到了如图3(b)和图3(f)所示的几乎相同的瞬时压力系数分布。耦合圆柱在点1和点3时虽然都在中心位置，但点1时结构将从中心位置向上振动，相反在点3时结构开始从中心位置向下振动，相反的运动方向使得各圆柱在两种情况下的瞬时压力关于θ=0°或θ=180°对称(见图3(b)和图3(d))。当在点2和点4时，耦合圆柱位移分别达到正的最大和负的最大，但运动方向也相反，同样也得到了如图3(c)和图3(e)关于θ=0°或θ=180°对称的瞬时压力系数分布图。由于上游圆柱受均匀来流的直接作用，而下游圆柱却受上游圆柱脱落涡冲击的影响，使得下游圆柱1和圆柱2的前缘部分(0°≤θ≤60°和300°≤θ≤360°内)的瞬时压力小于上游圆柱3和圆柱4。

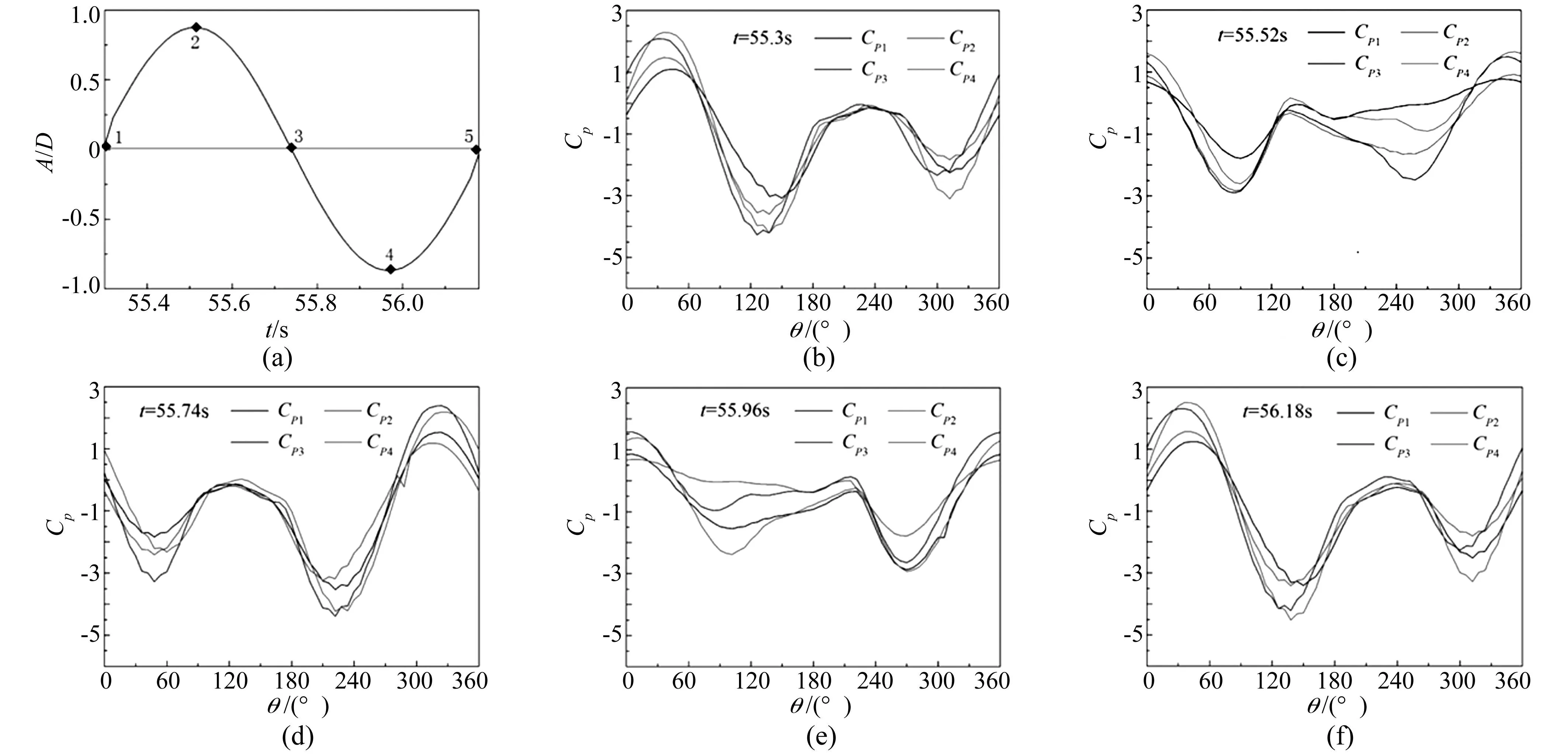
图3　各圆柱表面单个周期内的瞬时压力系数 Fig.3 Instantaneous pressure coefficients on each cylinder’s surface in single period

3.3水动能获取

单位时间单位长度圆柱系统从流体中获取的水动量用P表示：P=πFyfexAsinΦ(A为振幅，fex为圆柱系统激励频率，Fy代表升力幅值,Φ为振幅与升力间的相位差)。采用单位水流体积内所获得的能量，即能量密度这一参数可使表1中各方案下获取的能量更具可比性。由图1可知，L×H的水流截面内，包括1个圆柱，故单位长度水流体积的能量密度Pdensity为：Pdensity=P/4LH。 通过计算各组合间距比下的P和Pdensity值,得到图5的结果。由图可知，间距比的大小对圆柱系统从水流中获取的能量及能量密度影响较大。P随着组合间距比LH/D2的增加先增加较快，然而继续增加横向和流向间距比并不能使圆柱系统获得更多的能量：当LH/D2>6，且Ur=6和Ur=7时，获取的能量增加缓慢；在约化速度Ur=8时，P还呈现减少趋势；当2.25≤LH/D2≤5时，能量密度Pdensity随着LH/D2值的增加而增加，而当LH/D2>5时，由于获取的水动能增加很少，而圆柱系统所含的水体体积随着横向和流向间距的增加而增加，能量密度值减少。因此，对于这种耦合连接的四圆柱系统，若要充分利用海流能或河流能，可选取合理的横向和流向间距比，使圆柱系统从单位水体内获得更多的能量。

图4　不同间距比下各圆柱表面在的压力系数幅值 Fig.4 Amplitude of pressure coefficients on each cylinder’s surface under different spacing ratios

图5　各间距比下耦合四圆柱获取的水动能及能量密度 Fig.5 Energy harvesting and power density of four coupling-linked cylinders under different spacing ratios

4结论

本文借助流固双向耦合数值方法，对均匀来流条件下耦合连接四圆柱的涡激振动现象进行模拟。分析了12种组合间距比下各圆柱的升力和压力特性及从海洋流或河流中获取的水动能及能量密度。得到以下结论：

(1)无论间距比大小如何，耦合的四圆柱中，上端两圆柱的升力系数均值与下端两圆柱的升力系数均值关于0对称，但其升力系数均方根值却近似相等。且随着组合间距比的增加，各圆柱的升力系数均方根值越小。

(2)间距比L/D=4，H/D=2时，圆柱系统在相反运动方向时刻其瞬时压力系数关于θ=0°或θ=180°对称。且上端两圆柱的压力系数幅值在不同组合间距比时分别与下端两圆柱的压力系数幅值关于θ=180°对称。

(3)获取的水动能及能量获取密度随着组合间距比的增加先增加较快，继续增加横向和流向间距，获取的水动能增加缓慢，而获取能量密度却不断减少。因此，存在合理的横向和流向间距比，使圆柱系统从单位水体内获得更多的能量。

参考文献

[1]Bernitsas M M，Raghawan Y，Ben Simon E M H，et al. VIVACE (vortex induced vibration for aquatic clean energy)：A new concept in generation of clean and renewable energy from fluid flow[J].Journal of Offshore Mechanics and Arctic Engineering，2008，130 (4)：1-15.

[2]Barrero Gil A，Alonso G，Sanz Andres A. Energy harvesting from transverse galloping [J].Journal of Sound and Vibration，2010，329：2873-2883.

[3]Lee J H, Xiros N, Bernitsas M M. Virtual damper-spring system for VIV experiments and hydrokinetic energy conversion[J].Ocean Engineering, 2011, 38(5/6): 732-747.

[4]Bernitsas M M，Ben Simon Y，Raghavan K， et al. The VIVACE converter：model tests at high damping and Reynolds number around105[J]. Journal of Offshore Mechanics and Arctic Engineering，2009，131 (1)：1-12.

[5]Lam K, Gong W Q, So R M C. Numerical simulation of cross-flow around four cylinders in an in-line square configuration [J]. Journal of Fluids and Structures, 2008, 24:34-57.

[6]Lam K, Zou L. Experimental and numerical study for the cross-flow around four cylinders in an in-line square configuration [J]. Journal of Mechanical Science and Technology, 2007, 21:1338-1343.

[7]曲雪，薛鸿祥，唐文勇. 深海顶张式立管顺流涡激振动响应预报方法[J].振动与冲击，2013，32(15): 32-36.

QU Xue, XUE Hong-xiang, TANG Wen-yong. In-line VIV analysis of deep-water top tensioned riser [J].Journal of Vibration and Shock,2013,32(15):32-36.

[8]徐枫，欧进萍. 正三角形布置三圆柱绕流与涡致振动数值模拟[J]. 空气动力学学报，2010，28(5)：582-590.

XU Feng，OU Jin-ping. Numerical simulation of vortex-induced vibration of three cylinders subjected to a cross f low in equilateral arrangement [J]. Acta Aerodynamic Sinica，2010，28(5)：582-590.

[9]Lam K, Zou L. Three-dimensional numerical simulations of cross-flow around four cylinders in an in-line square configuration [J]. Journal of Fluids and Structures, 2010,26：482-502.

[10] Zou L, Lin Y F. Flow patterns and force characteristics of laminar flow past four cylinders in diamond arrangement [J]. Journal of Hydrodynamics, 2011, 23(1):55-64.

[11]Zhao M, Cheng L. Numerical simulation of vortex-induced vibration of four circular cylinders in a square configuration[J/OL]. Journal of Fluids and Structure.[2012-04-02]. http://dx.doi.org/10.1016/j.jfluidstructs.2012.04.002.

[12]罗竹梅，张立翔. 基于流固双向耦合的圆柱体涡激振动模拟[J].昆明理工大学学报，2013,38(3):107-112.

LUO Zhu-mei, ZHANG Li-xiang. Numerical simulation of vortex-induced vibration of cylinder based on two-way fluid-structure coupling [J]. Journal of Kunming University of Science and Technology, 2013, 38(3): 107-112.