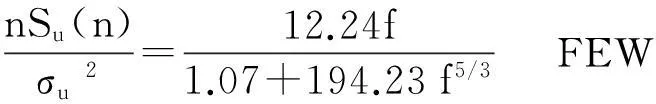基于设计基准条件的台风边界层脉动风速谱建模方法研究
李利孝,肖仪清,周超英,宋丽莉
(1.哈尔滨工业大学深圳研究生院,广东 深圳 518055; 2.公共气象服务中心中国气象局,北京 100081)
第一作者李利孝男,博士,1984年生
基于设计基准条件的台风边界层脉动风速谱建模方法研究
李利孝1,肖仪清1,周超英1,宋丽莉2
(1.哈尔滨工业大学深圳研究生院,广东深圳518055; 2.公共气象服务中心中国气象局,北京100081)
摘要:利用在博贺峙仔岛观测站实测的台风黑格比数据,在莫宁-奥布霍夫相似理论框架内提出了一种数据驱动的考虑设计基准条件的台风边界层脉动风速谱建模方法。首先基于均匀各向同性湍流能谱需满足的基本模型准则,将六参数脉动风速谱统一模型简化为四参数谱模型;之后基于高频区和低频区脉动风速谱特征建立了四个谱参数的理论表达式,并利用实测的台风黑格比数据将谱参数理论表达式进行参数化处理,进而提出基于设计基准条件的脉动风速谱建模方法;最后利用台风黑格比过程中任意选取的四个1h时长样本对上述脉动风速谱建模方法进行了验证,表明其与实测样本的风速谱具有较好的一致性。
关键词:台风;湍流;脉动风速谱;设计基准条件;结构抗风设计
基金项目:国家自然科学基金(51308168和51278161);中国博士后科学基金项目(2013M531045)
收稿日期:2014-01-08修改稿收到日期:2014-05-30
通信作者肖仪清男,博士,教授,1973年生
中图分类号:TU973+.32
文献标志码:A
DOI:10.13465/j.cnki.jvs.2015.11.003
Abstract:A data-driven model was proposed to model wind velocity spectrum of typhoon boundary layer considering conditions of design reference. This model was established based on Moning-Obukhov similarity theory (MOST) and the field measured data of typhoon Hagupit on Zhizai Island, Bohe. Firstly, the six-parameter general model was simplified into a four-parameter spectral model by matching the model criteria of energy spectrum in homogeneous turbulent flow. Secondly, the theoretical expressions of the four spectral parameters were determined based on the features of wind velocity spectrum in lower and higher frequency ranges. Then the data-driven model considering conditions of design reference was established through parameterizing the four spectral parameters with the field measured data of typhoon Hagupit. Finally, the validation of the data-driven model was examined with arbitrarily selected four 1-hour length data sets in the process of typhoon Hagupit. It was shown that the wind velocity spectrum modeled using the proposed method agrees well with that obtained using the actual measured samples.
Modeling method for fluctuating wind velocity spectrum in typhoon boundary layer based on conditions of design reference
LILi-xiao1,XIAOYi-qing1,ZHOUChao-ying1,SONGLi-li2(1. Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen 518055, China;2. Public Meteorological Service Center, China Meteorological Administration, Beijing 100081, China)
Key words:typhoon; turbulence; wind velocity spectrum; conditions of design reference; wind-resistance design
大量超高层建筑和超大跨度桥梁结构在我国东南沿海地区兴建,每年遭受若干次台风的袭击,使得抵抗台风作用成为这类结构在服役期安全性和舒适性的巨大挑战。准确刻画台风风场结构特征和湍流特性是估计台风风荷载和抗台风设计的首要保证。风速剖面刻画了平均风速随高度的变化规律,是估算平均风荷载的重要参数,而风速谱则表征了湍动能在不同频率区段上的分布特征,是刻画脉动风荷载的关键参数[1-2]。
目前国内外大部分风荷载规范所采用的经验风速谱模型[3-5]是利用非气旋风场实测数据基于均匀各向同性湍流的能谱特征推导所得,然而在台风场中,对流湍流和下沉作用将风场上部形成的大尺度涡漩向下输运并影响近地面层的流场特性,使得台风风场与常态风风场在结构特征和湍流特性均存在一定的差异[6-9]。针对台风场脉动风速谱特征,国内外学者开展了大量的实测研究,部分学者的观测发现台风场脉动风速谱包含较多的低频区能量,含能区特征尺度大于常态大风风场的特征尺度[10-11];而另一部分学者则获得与之相反的结论[12-13]。鉴于此,部分学者采用最小二乘法对实测台风场数据进行拟合以获得适用于台风影响区的脉动风速谱模型[14-15]。然而,采用这种拟合方法所建立的谱模型的参数变异性较大,对实测数据依赖性较高;同时所建立的谱模型不能直观反映风场环境、粗糙度类别、高度以及风速等结构设计基本条件的影响,也不能反映大气层结稳定度等气象学要素对谱特性的影响[16]。
因此,本文将基于在博贺峙仔岛观测站实测的台风黑格比数据,提出一种数据驱动的基于设计基准条件的台风边界层脉动风速谱建模方法,并利用台风黑格比过程中任意选取的四个1h时长的样本对上述建模方法的准确度进行验证,从而为台风影响区建筑结构的抗风设计提供借鉴和指导。
1脉动风速谱理论模型建立
均匀各向同性湍流的湍能谱可划分如下三个区域:含能区、惯性子区和能量耗散区(见图1)。含能区主要通过大尺度漩涡的脉动从平均流中获取能量,其包含了流场绝大部分的湍动能;能量耗散区则主要是通过小尺度漩涡的相互摩擦碰撞作用进行能量的耗散;而在惯性子区,假定漩涡主要进行能量的传递作用,既不从平均流中获取能量,也不进行能量的耗散[17]。所以在惯性子区,归一化的脉动风速谱服从各向同性湍流的-2/3次律变化规律[18],
(1)
式中:Su(n)为脉动风速谱谱;u*为摩擦速度;φε为无量纲化风切力的莫宁奥布霍夫系数函数;Au为常数,取为0.27;n为自然频率(Hz);f为无量纲化折算频率,f=nΛ/U,其中Λ可为离地高度,积分尺度或一固定值。
基于惯性子区的脉动风速谱一般形式(式(1)),大量大气中性层结下的经验风速谱模型在此基础被提出并广泛应用于不同国家的抗风设计规范中,这些经验谱模型可统一表达为六参数脉动风速谱广义模型,即
(2)
式中:A、B、C、α、β和γ为六个待定参数;R为湍流比。

图1 均匀各向同性湍流湍能谱示意图Fig.1 Schematic of energy spectrum of homogeneous and isotropic turbulence
1.1模型准则
基于莫宁-奥布霍夫相似理论和均匀各向同性湍流的基本特征,脉动风速谱统一模型(式2)需满足以下几个基本准则:
(1)在惯性子区脉动风速谱需服从Kolmogorov的-2/3次律能量传递理论,即
αβ-γ=2/3
(3)

γ=1;A=4Cβ
(4)
(3)当频率n趋近于0时,脉动风速谱Su(n)的导数亦趋近于0,由此可得
α≥1
(5)
将式(3)~式(5)代入式(2),则六参数脉动风速谱广义模型可简化为四参数谱模型,即
(6)
式中:A、B、C和α为四个待定参数。
1.2谱参数理论模型
无量纲化的顺风向脉动风速谱nSu(n)/u*2在低频区服从折算频率f的+1次律变化规律,在惯性子区则服从折算频率f的-2/3次律变化规律。因此无量纲化的脉动风速谱则可通过如下四个谱参数来确定:无量纲化脉动风速谱在谱能量达到最大值时对应的折算频率fm和谱能量Gm(Gm=max(nSu(n)/σ2)),无量纲化风速谱在惯性子区系数Au,归一化脉动风速谱的湍流比R。
上述四个谱参数则可由四参数谱模型(式(6))的四个待定参数来表达:
(1)无量纲化脉动风速谱在谱能量达到最大值时对应的折算频率fm可通过对式(6)右边部分求导得,
(7)
(2)归一化风速谱在双对数坐标系中的最大谱密度Gm则可表示为
(8)
(3)在惯性子区,脉动风速谱系数Au可由下式计算
(9)
(4)由顺风向脉动风速谱所包含的能量等于顺风向脉动风速的方差可得
(10)
式中
s≠0, -1, -2…
(11)
由上述分析可知,当描述风速谱形的四个谱参数确定之后,即可通过联解式(7)~式(10)进而反算求得四参数谱模型(式(6))中的四个待定参数A、B、C和α,从而可建立一个相应的脉动风速谱的表达式。
2脉动风速谱参数模型建立
2.1数据来源
本文所采用的数据为2008年第14号台风黑格比在博贺峙仔岛观测站实测得台风资料。强台风黑格比是自1996年以来登陆广东的最强台风,于2008-09-24T06∶45在广东省西部电白县陈村附近登陆,登陆时中心最大风力15级(48m/s)。强台风黑格比数据是由广东省气象局在博贺峙仔岛100 m观测塔进行现场实测的所得,观测站场地条件以及仪器设置等可见参考文献[19-20]。
图2所示为峙仔岛观测站60 m高度的超声风速仪实测的强台风黑格比的风速风向时程,由图可见强台风黑格比风眼经过了观测站,在中心经过前后的风向转角约为191°,台风中心经过前的最大10min平均风速为45.88 m/s,台风中心经过后的最大10min平均风速为40.11 m/s。实测的台风黑格比144个样本经过了数据质量控制和样本选取准则处理后[20],最终有47个满足平稳性要求的样本用于本文的分析。
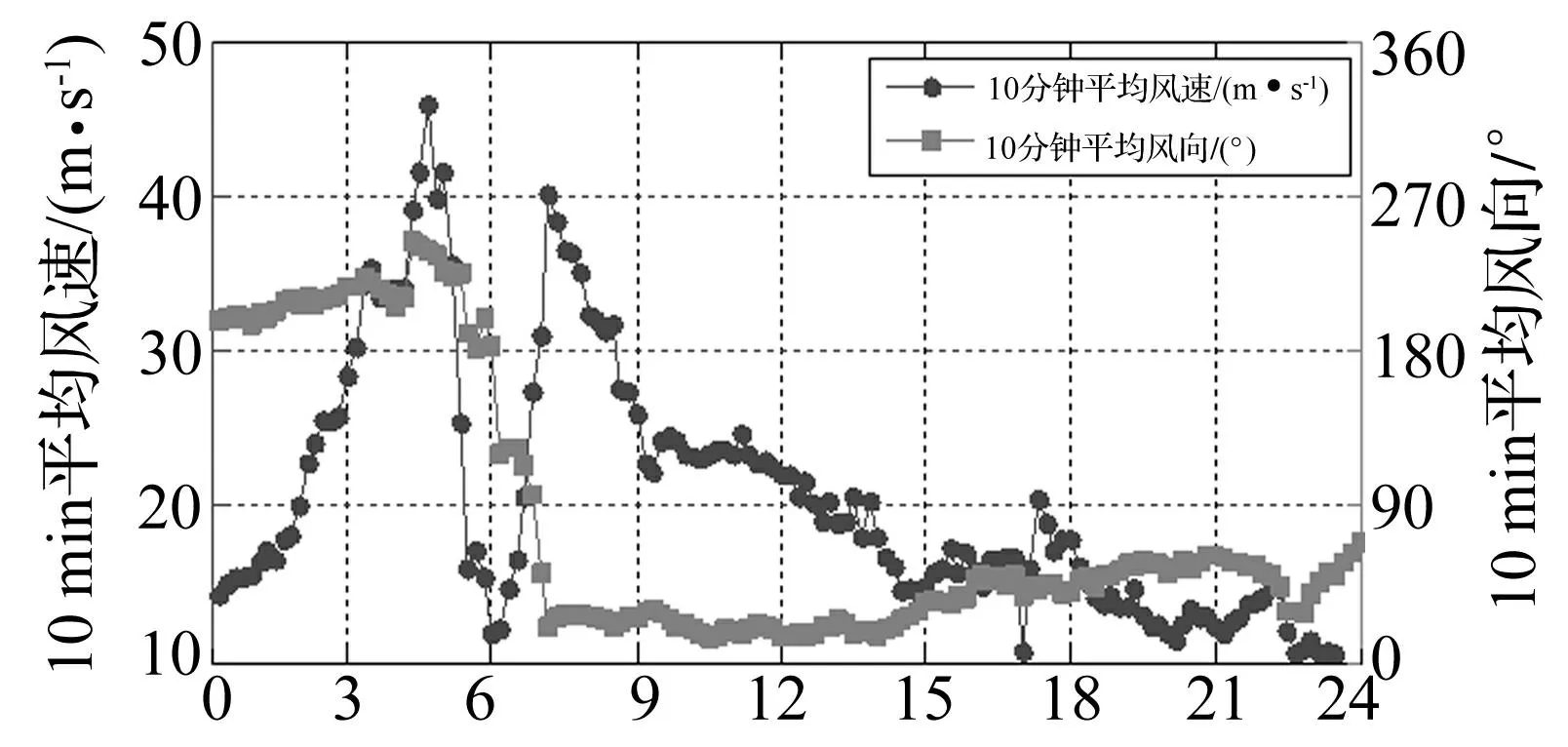
图2 台风黑格比10分钟平均风速风向时程Fig.2 Time history of 10 min mean wind speeds and directions in typhoon Hagupit
2.2谱参数经验模型建立
由1.2节的分析可知,只要确立了四个谱参数,即可通过式(7)~式(10)来确定参数A、B、C和α,本节将基于上节所选取的47个数据样本,采用最小二乘法拟合建立各谱参数的经验模型。由于大气稳定度对风速谱在低频区的能量分布较大程度的影响,在本节的分析中将同时考虑大气层结稳定度对谱参数的影响。
在莫宁-奥布霍夫相似理论框架内,大气层结稳定度可通过无量纲化的大气稳定度系数来表达,即
(12)
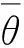
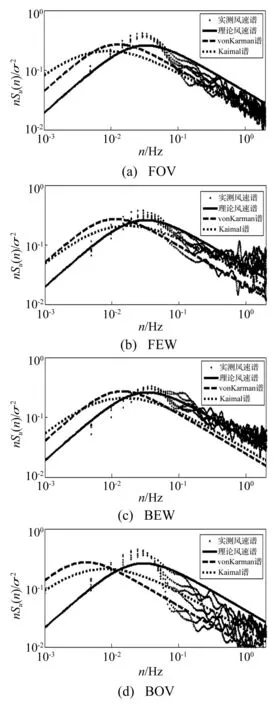
在式(12)中,当z/L>0时为稳定层结,z/L<0时为不稳定层结,z/L=0时为中性层结。由于z/L=0的样本基本上没有,所以在本文中假定-0.1 基于莫宁-奥布霍夫相似理论分析时认为湍流比R在近面地层不随高度发生变化,但随着场地粗糙度的改变而改变,同时其还受到大气层结稳定度的影响。在本文的分析中,先选取中性层结样本研究湍流比随粗糙度长度的变化规律,之后再分析湍流比随大气层结稳定的变化关系。 图3(a)为实测的中性层结样本中湍流比随粗糙度长度的变化规律,为了比较台风风场中风眼经过前后区域的湍流比差异,将所选样本又划分为中心经过前和中心经过后两个类别,分别采用最小二乘拟合得湍流比随粗糙度长度的关系如下两式所示 TR(z0)=2.74-0.17ln(z0) (13) TR(z0)=0.65-0.28ln(z0) (14) 图3(b)为大气稳定度参数对湍流比的影响,在分析大气稳定度对湍流比的影响时,先利用式(13)扣除粗糙度长度对湍流比的贡献,之所以选择式(13)是因为在台风中心经过后所选取到的近中性层结样本基本上均位于外环流区域,不能代表台风风场特性。叠加粗糙度长度对湍流比的影响和大气稳定度对湍流比的影响之后,湍流比可表达为 R(z0,z/L)=2.74-0.17ln(z0)+0.93(z/L)1/3 (15) 图3 湍流比TR随粗糙度长度z0和大气稳定度参数z/L的变化关系Fig.3 Variation of turbulence ratio with roughness length z0and atmospheric stability z/L 类似于湍流比,折算频率fm也采用了相应的分析方法进行分析,图4(a)所示为谱密度峰值Gm对应的自然频率nm随平均风速U的变化关系。在分析二者之间的关系时,只选用了近中性层结的样本,利用最小二乘回归得二者之间的关系为 nm=0.024 4exp(0.006 6U) (16) 图4(b)所示为大气层结稳定度对频率nm的影响。类似于分析大气稳定度对湍流比的影响,在这里亦先利用式(16)扣除了平均风速对频率nm的影响,综合平均风速以及大气稳定度对频率nm的影响,可得如下表达式, nm=0.024 4exp(0.006 6U)+ (17) 与之相对应的折算频率fm则可表示为 fm=U-1z(0.024 4exp(0.006 6U)+0.020 8z/L) (18) 式中:U为平均风速,0≤z/L≤0.4。 图4 频率nm随平均风速U和大气稳定度参数z/L的变化关系Fig.4 Variation of natural frequency nmwith mean wind speed U and atmospheric stability z/L 实测的归一化风速谱的谱密度最大值Gm没有表现出明显的随粗糙度长度或大气稳定度的变化规律,所以在这里只分析了Gm随平均风速U的变化关系,见图5。利用最小二乘法拟合得Gm与平均风速U的变化关系如下式所示 Gm=0.748 5/U0.233 4 (19) 图5 谱密度最大值Gm随平均风速U的变化关系Fig.5 Variation of the maximum of normalized wind velocity spectra, Gm, with mean wind speed U 图6为惯性子区脉动风速谱参数Au随平均风速U的变化关系。由图6可见,台风风场顺风向风速谱谱参数的实测值较为离散且大于理论推导的值0.26。谱参数的实测值是基于式(1)利用最小二乘法拟合惯性子区的实测风速谱而得到的,谱参数的实测值与平均风速的关系可用下式表示 Au=0.011 3U1.177 0+0.177 8,U≥17.2 m/s (20) 图6 惯性子区谱参数Au随平均风速U的变化关系Fig.6 Variation of Auin inertial subrange with mean speed U 利用上述各谱参数的经验模型(式(15)、式(18)、式(19)和式(20)),基于设计基准条件(设计基准风速、场地类别和大气稳定度条件)可确定各谱参数的具体取值,进而利用1.2节所建立的理论模型(式(7)~式(10))反算得四参数风速谱模型(式(6))的四个待定参数,最后可确定唯一的风速谱表达式。 3模型有效性验证 3.1数据选取 本文2.2节的谱参数模型是建立在平稳样本的基础上,为了使上述脉动风速谱建模方法不失一般性,在这里任意选取了强台风黑格比风场不同部位(前外环流区FOV、前眼壁区FEW、后眼壁区BEW和后外环流区BOV)的四个时长为1h的样本进行分析,所选的四个1h样本的详细湍流统计特性列于表1中。 3.2模型有效性验证 基于表1所列的各样本的平均风速及其湍流统计参数,分别采用式(15)、式(18)、式(19)和式(20)计算了各样本的湍流比TR、折算频率fm、归一化风速谱谱密度最大值Gm和惯性子区谱参数Au(见表2)。 表1 四个1h时长样本的湍流统计特性 表2 四个1h时长样本的谱参数 基于表2所计算得谱参数,采用“1.2”节所建议的理论谱模型建立了强台风黑格比不同部位的脉动风速谱表达式,如下各式所示: (21) (22) (23) (24) 图7 ((a)、(b)、(c)和(d))分别给出了强台风黑格比四个区域的实测风速谱、理论风速谱(式(21)~式(24))、von Karman谱和Kaimal谱进行对比。由图7可见,采用本文建立的方法确定的风速谱(图例中称作理论风速谱)与实测风速谱吻合的非常好,尤其是在眼壁强风区(FEW和BEW)。在外环流区域(FOV和BOV),理论风速谱与实测风速谱有一定的差异,这可归结为如下三个原因:第一个是由于样本的非平稳性导致的,四个1h时长样本是任意选取的,有些样本不满足平稳性要求;第二个可归结为大气稳定度的影响,本文在确定风速谱模型时选用了1h总样本的稳定度参数,但是在1h内的6个10min时长的子样本则有的是稳定层结,有的是不稳定层结;第三个原因可归结为建立谱参数经验模型的数据量相对较少,准确性需进一步提高。 图7 实测风速谱与理论谱以及经验风速谱对比Fig.7 Comparison of field measured spectra, theoretical model spectra and empirical spectra 4结论 通过对大气边界层顺风向脉动风速谱统一表达式的分析,在莫宁-奥布霍夫相似理论的框架内和局部均匀各向同性湍流理论的基础上提出了一种基于设计基准条件的台风风场边界层风速谱建模方法,并验证了该方法的准确性,得出如下主要结论: (1)通过对顺风向脉动风速谱需满足的基本条件分析,从理论上将六参数风速谱模型简化为四参数风速谱模型,并提出了基于四个谱参数的建模方法; (2)利用实测的强台风黑格比的数据,建立了谱参数的数学模型,将其参数化为平均风速、粗糙度长度、大气稳定度参数的函数; (3)利用任意选取的四个一小时时长的台风风场数据,验证了该建模方法所确立的脉动风速谱模型的准确性,发现该理论模型与实测风速谱吻合较好,优于各经验风速谱模型与实测台风风速谱的一致性。 本文所提出台风脉动风速谱建模方法是一种数据驱动模型,对谱参数经验模型的准确性依赖度较高,所以有必要继续扩大数据量以更为准确的模拟各谱参数经验模型,更为精确的确立不同设计基准条件的风速谱模型。另外本文所建立的风速谱建模理论亦适用于竖向脉动风速谱的建模分析和非气旋风场的风速谱建模。 参考文献 [1]Li L, Kareem A, Xiao Y, et al. Wind profile and spectra in typhoon-prone regions in south China [C]. Miami, Florida, America: American Society of Civil Engineers, 2012. [2]李利孝,肖仪清,宋丽莉,等. 基于风观测塔和风廓线雷达实测的强台风黑格比风剖面研究[J]. 工程力学,2012, 29(9): 284-293. LI Li-xiao, XIAO Yi-qing, SONG Li-li, et al. Study on wind profile of typhoon Hagupit using wind observed tower and wind profile radar measurements[J]. Engineering Mechanics,2012, 29(9): 284-293. [3]Kaimal J C, Wyngaard J C, Izumi Y, et al. Spectral characteristics of surface-layer turbulence[J]. Quarterly Journal of the Royal Meteorological Society,1972, 98(417): 563-589. [4]Davenport A G. The spectrum of horizontal gustiness near the ground in high winds[J]. Quarterly Journal of the Royal Meteorological Society,1961, 87(372): 194-211. [5]Karman T V. Progress in the statistical theory of turbulence[J]. Proc Natl Acod Sci U S A.,1948,34(11):530-539. [6]Bradbury W, Deaves D M. The dependence of gust factor probabilities on convective activity: Analysis conducted for Eurotunnel[J]. Meteorological Applications,1994, 1(2): 159-164. [7]Sparks P R, Huang Z. Gust factors and surface-to-gradient wind-speed ratios in tropical cyclones[J]. Journal of Wind Engineering and Industrial Aerodynamics,2001, 89(11/12): 1047-1058. [8]Powell M D, Houston S H. Hurricane andrew’s landfall in south florida. part Ⅱ: surface wind fields and potential real-time applications[J]. Weather and Forecasting,1996, 11(3): 329-349. [9]Li L, Xiao Y, Song L. Observed sub-hectometer-scale boundary layer rolls in surface layer in landfalling typhoons[C]//Robinson College, Cambridge, UK,2013. [10]Schroeder J L, Smith D A. Hurricane Bonnie wind flow characteristics as determined from wemite[J]. Journal of Wind Engineering and Industrial Aerodynamics. 2003, 91(6): 767-789. [11]Yu B, Gan Chowdhury A, Masters F. Hurricane wind power spectra, cospectra, and integral length scales[J]. Boundary-Layer Meteorology,2008, 129(3): 411-430. [12]Li L, Xiao Y, Kareem A, et al. Modeling typhoon wind power spectra near sea surface based on measurements in the south China sea[J]. Journal of Wind Engineering and Industrial Aerodynamics,2012, 104-106: 565-576. [13]Zhang J A. Spectral characteristics of turbulence in the hurricane boundary layer over the ocean between the outer rain bands[J]. Quarterly Journal of the Royal Meteorological Society,2010, 136(649): 918-926. [14]胡晓红,葛耀君,等. 上海“派比安”台风实测结果的二维脉动风谱拟合[J]. 结构工程师, 2002(2): 41-47. HU Xiao-bong, GE Yao-jun, PANG Jia-bin. The fitting of 2D fluctuating wind spectrum for the actual measurement data of “pha” typhoon in Shanghai[J].Structural Engineers,2002(2): 41-47. [15]黄鹏,戴银桃,王旭,等. 上海沿海地区近地风脉动风速谱及相干性研究[J]. 工程力学, 2014(4): 126-133. HUANG Peng, DAI Yin-tao, WANG Xu,et al. Field measurement on power spectra and coherence characteristics of near-ground wind in shanghai coastal area[J].Engineering Mechanics, 2014(4): 126-133. [16]李利孝. 热带气旋边界层风场剖面和工程湍流特性研究[D]. 哈尔滨:哈尔滨工业大学, 2012. [17]Kaimal J C, Finnigan J J. Atmospheric boundary layer flows: their structure and measurement[M]. Oxford, New York: Oxford University Press, 1994. [18]Simiu E, Scanlan R H. Wind effects on structure: fundamentals and applications to design[M]. Now York: John Wiley & Sons, 1996. [19]Song L, Li Q S, Chen W, et al. Wind characteristics of a strong typhoon in marine surface boundary layer[J]. Wind and Structures,2012, 15(1): 1-15. [20]肖仪清,李利孝,宋丽莉,等. 基于近海海面观测的台风黑格比风特性研究[J]. 空气动力学学报, 2012, 30(3): 380-387. XIAO Yi-qing, LI Li-xiao, SONG Li-li,et al.Study on wind characteristics of typhoon Hagupit based on offshore sea surface measurements[J].Acta Aerodynamica Sinica, 2012, 30(3): 380-387.