操纵面非线性气动弹性响应引起的结构疲劳损伤分析方法研究
李 毅 ,杨智春 ,金 伟
(1. 西北工业大学航空学院结构动力学与控制研究所, 西安 710072; 2.成都飞机设计研究所,成都 610091)
第一作者李毅男,博士生,1982年生
操纵面非线性气动弹性响应引起的结构疲劳损伤分析方法研究
李毅1,杨智春1,金伟2
(1. 西北工业大学航空学院结构动力学与控制研究所, 西安710072; 2.成都飞机设计研究所,成都610091)
摘要:由于间隙的存在,随着速度的增加操纵面会发生非线性气动弹性响应,即操纵面发生极限环振动,其振动频率比飞机结构疲劳载荷谱的频率高,因此操纵面在每次飞行中只需经历1~2 s的极限环振动,其在整个飞机服役期内累加得到的总循环数将达到10万次的量级,可见操纵面极限环振动引起的结构疲劳损伤不容忽视,所以需要建立起操纵面气动弹性数据(飞行速度和间隙)与结构疲劳损伤的对应关系。针对此问题,将非线性气动弹性分析方法和结构疲劳预测技术结合,发展一套分析流程用来讨论操纵面极限环振动与周边结构疲劳的关系,为设定操纵面间隙值提供参考。为了对此分析流程进行说明,对具有操纵面的复杂机翼进行了非线性气动弹性分析获得其偏转角响应,并将其转化为作用在作动器两头耳片上的疲劳载荷谱,通过疲劳分析获得周边结构疲劳特性与操纵面非线性气动弹性响应的关系。
关键词:操纵面;间隙;极限环振动;疲劳损伤
收稿日期:2013-11-08修改稿收到日期:2014-06-17
通信作者杨智春男,博士,教授,博士生导师,1964年生
中图分类号:V211.47
文献标志码:A
DOI:10.13465/j.cnki.jvs.2015.11.008
Abstract:Due to free play, aeroelastic response of a control surface is nonlinear, limited cycle vibration (LCO) occurs on the control surface. Frequencies of LCO are higher than those of fatigue load spectrum of a plane structure, the total vibration cycle number of the control surface with in a plane’s lifetime will be more than one hundred thousand times, and the fatigue damage of the control surface induced by LCO has to be taken into account. Thus the relationship between the aeroelastic data of the control surface (free play and velocity) and structural fatigue damage should be established. Here, based on the nonlinear aeroelastic analysis and the structural fatigue analysis, an analysis procedure was developed to study the relationship between LCO of the control surface and structural fatigue damage, and this analysis procedure could guide the setting of free play. In order to illustrate this method, the rotational angle responses of a control surface were obtained with the nonlinear aeroelastic analysis. Based on these responses, the fatigue load spectrum was gained. Finally, the structural fatigue analysis was performed to obtain the relationship between the fatigue damage features of the periphery structures and the nonlinear aeroelastic response of a control surface.
Analysis method of structural fatigue damage induced by nonlinear aeroelastic response of control surface
LIYi1,YANGZhi-chun1,JINWei2(1. Institute of Structural Dynamics and Control, School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China;2. Cheng Du Aircraft Design and Research Institute, Cheng Du 610091, China)
Key words:control surface; free play; LCO; fatigue damage
飞机操纵面系统中的间隙会引起操纵面的极限环振动,为了避免极限环振动的发生,飞机工程实践中一般采用以下手段:①对间隙值进行严格限定,保证在整个飞行包线内都不出现极限环振动,但这必然会带来过高的制造成本和维护费用;②对飞行速度进行限制,但这又会造成飞行性能的降低。为了解决这一矛盾,国外航空先进国家在现代高性能战斗机设计和使用中,已经开始探索放宽操纵面间隙值限制的技术。比如美国在F-22飞机的操纵面设计和使用中,允许操纵面可以发生小幅值的极限环振动,但规定引起的铰链力矩不可以超过±10%的限制铰链力矩[1]。从疲劳载荷谱幅值看,这样的规定是为了防止操纵面的极限环振动过大而引起操纵面周边结构的疲劳问题;另一方面,操纵面极限环振动的频率比飞机结构疲劳载荷谱的频率高,即使操纵面在每次飞行只经历1~2 s的极限环振动,其在整个飞机服役期内累加得到的总循环数将达到10万次的量级,可见其引起的结构疲劳损伤不容忽视,所以需要建立起操纵面气动弹性数据(飞行速度和间隙)与结构疲劳损伤的对应关系。
Van Muijden[2]曾经研究过极限环振动对F-16飞机结构疲劳和裂纹扩展的影响问题外,贺尔铭[3]对热声载荷作用下,发生非线性振动的薄壁结构的疲劳寿命预测方法进行了研究,在气动弹性领域也有许多学者[4]对间隙非线性存在下的结构响应进行了研究,但是将非线性气动弹性和疲劳寿命预测两个领域相互耦合的研究工作并不多见。
本文将非线性气动弹性分析方法和结构疲劳分析技术结合,形成一种分析操纵面极限环振动与其周边结构疲劳关系的分析流程。由于操纵面与主翼面之间存在较大空隙,导致气流分离,并且当操纵面发生LCO时,其偏转角度较大,难于保证气动网格的精度,因此权衡精度和效率后,业内推荐采用通过Roger拟合后的非定常气动力[5-6],本文在气动弹性分析中也采用了此种气动力模型。从飞机设计的工程意义上讲,该方法获得的飞行速度、间隙与结构疲劳损伤的关系,可以为操纵面极限间隙值的确定提供参考。文中以一个带操纵面的后掠机翼为对象,对所提出的分析流程进行了详细的阐述和演示。
首先对其进行非线性气动弹性分析,获得操纵面发生极限环振动时的偏转角响应,通过有限元模拟将响应的峰谷值转化为作用在操纵面作动器两端耳片上的疲劳载荷谱,随后进行疲劳分析,最终获得耳片结构的疲劳特性与极限环振动特性的关系。
1分析方法
本文采用如下分析方法来研究操纵面气动弹性与结构疲劳损伤之间的关系(见图1)。
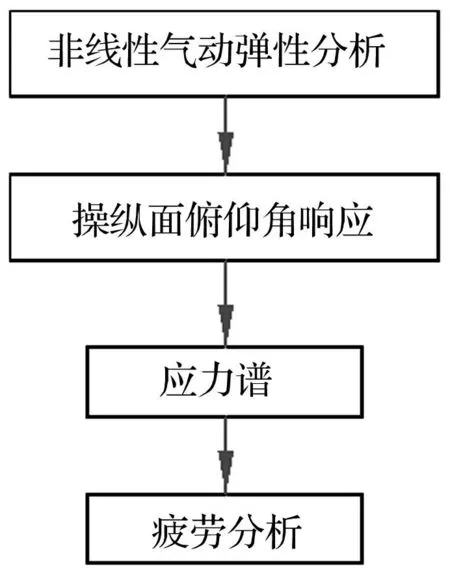
图1 分析流程图Fig.1 Analytical procedure
首先,通过非线性气动弹性分析获得操纵面极限环振动的时域响应。然后通过有限元模拟将响应的峰谷值转化为其周边结构上的疲劳载荷,通过静力计算获得结构中疲劳关键位置上的疲劳载荷谱。最后,通过疲劳分析得到对应于该极限环振动幅值下的结构疲劳特性。
2分析模型与非线性气动弹性分析
本文所采用的分析模型为一个带操纵面的后掠机翼,机翼结构的有限元模型见图2,假定其操纵刚度带有中心间隙型非线性(见图3),其中α为偏转角,M为恢复力矩,Kα为线性操纵刚度,间隙值为2δ。


图2 机翼模型Fig.2Wingmodel图3 中心间隙型操纵刚度Fig.3Controlstiffnessofcentralfreeplay
对带中心间隙型非线性操纵刚度的操纵面系统,在对称间隙区间[-δ,δ]内,对应的操纵刚度为零,操纵面可自由旋转;而在该区间外则对应线性操纵刚度(称为名义操纵刚度或设计操纵刚度)。该非线性刚度模型可用分段线性函数表示为[7]:
(1)
为了对含中心间隙型非线性操纵刚度的机翼进行气动弹性分析,本文通过构建机翼的状态空间气动弹性方程,从而求解得到机翼的气动弹性响应。
首先计算出不同减缩频率下非定常气动力影响系数矩阵(QHHL),用Roger方法对其进行拟合[8]。
[Q(k)]=[A1]+[A2](ik)+[A3](ik)2+
(2)
这里,M一般取4,γ1=0.2,γ2=0.4,γ3=0.6,γ4=0.8,存在集中非线性刚度环节的机翼气动弹性运动方程为:
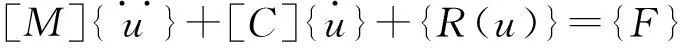
(3)
这里{R(u)}是弹性恢复力向量,其非线性恢复力可以表示为:

(4)
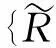
(5)
将方程(3)转换到模态坐标系下:

(6)

[GR(u)]=[GK]{u}+{φb}T{f(α)}
(7)
式中:({φb}为模态向量)
定义如下状态变量和矩阵:
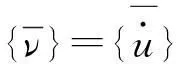

于是,可以得到状态空间气动弹性方程如下:
(8)
求解方程(8)便可以得到机翼的非线性气动弹性响应。
为了分别讨论间隙量和速度对极限环振动幅值及其周边结构疲劳特性的影响,分别分析了相同操纵面间隙不同飞行速度和相同飞行速度不同操纵面间隙工况下的极限环振动响应,结果见表1和表2。

表1 维持间隙量不变,改变飞行速度

表2 保持速度不变,改变间隙量

图4 41.8 m/s速度下操纵面偏转角响应(0.2°间隙)Fig.4 Rotational response of control surface (free play=0.2degree,velocity=41.8m/s)
3疲劳载荷谱的生成
为了得到操纵面作动器两端耳片上的疲劳载荷谱,还需要完成以下4个步骤的工作:
(1)首先,要确定操纵面发生极限环振动时,操纵面作动器两端耳片上对应的载荷工况。操纵面偏转角响应曲线上的波峰和波谷分别对应于操纵面作动器作用在耳片上的拉载荷和压载荷见图5。通过气动弹性分析,从0.2°间隙、41.8 m/s速度时的操纵面偏转角响应曲线中截取一段,当操纵面偏转角达到0.4°的波峰时,作动器作用在耳片上的载荷也将达到极值,故选取此时为作用在耳片上疲劳载荷工况Ⅰ;类似当操纵面偏转角达到-0.4°波谷时为作用在耳片上疲劳载荷工况Ⅱ;同时从图5可以看到疲劳载荷的周期为0.05 s。

图5 操纵面极限环振动导致耳片疲劳的载荷工况选取Fig.5 Fatigue load case induced by LCO of control surface
(2)确定疲劳载荷工况中作用在耳片上的疲劳载荷值。所分析的操纵面及其周边结构的示意图(见图6),在1、2和3点处为有限元结点,1~3结点用模拟作动器的杆单元连接,2~3结点用模拟操纵面的刚性单元连接,所建立的有限元模型见图7。在结点2上施加垂直面内的弯矩,使刚性单元产生前述的波峰和波谷所对应的偏转角度,提取此时模拟作动器的杆单元13在结点1的结点力就是作用在耳片A上的疲劳载荷;提取杆单元13在节点3的结点力就为作用在耳片B上的疲劳载荷见表3。

图6 操纵面结构示意图Fig.6 Structure of control surface

操纵面偏转角度/(°)Fx/NFy/N0.244966800.3661210000.489921360
(3)细节应力计算。建立耳片A和耳片B的有限元模型(耳片材料为2024T3)(见图8)。施加表3中的疲劳载荷并将耳片根部固支,通过有限元分析便可以得到操纵面发生极限环振动时耳片上对应疲劳载荷工况下的应力分布(见图9),图9中给出的是操纵面极限环振动偏转幅值为0.3°时的情况。并取得疲劳关键位置处(图9~图10中圆圈位置)的最大主应力(见表4和表5)。

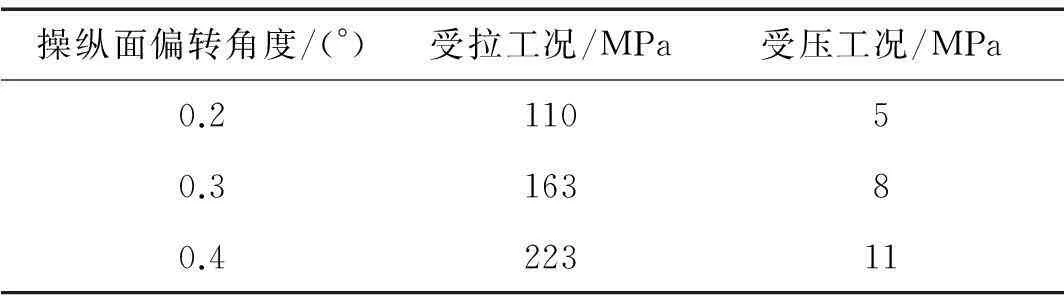
表5 耳片B上疲劳关键位置处的主应力
注:(FCL: fatigue critical location)
(4)根据细节应力计算的结果,并同时考虑极限环振动的时间历程和飞机使用情况来生成关键部位的疲劳载荷谱。首先,根据图5和表4可知,操纵面在极限环振动过程中经过中立位置时耳片上的应力为0(图11中A’),对应关系如见12。即在操纵面偏转角达到峰值和谷值时,所选疲劳关键位置(见图9和图10)的应力并不是最小值,而是当操纵面经过中立位置时,应力值将达到最小值0。所以在生成疲劳关键部位的疲劳载荷谱时应该将图11中B点去掉,直接连接A-A’-C;其次,假定该飞机的设计寿命为3 000个起落,若每次飞行中操纵面出现极限环振动的时间为2 s,由于操纵面极限环振动的周期为0.05 s,所以该飞机在设计寿命内作动器两端耳片要经受120 000个由于操纵面极限环振动导致的载荷循环,则耳片在操纵面发生不同幅值的极限环振动时,疲劳关键部位的疲劳载荷谱见表6和表7,谱型见图12。

表6 耳片A上疲劳关键位置处的疲劳载荷谱

表7 耳片B上疲劳关键位置处的疲劳载荷谱

图11 操纵面偏转角响应和疲劳载荷谱的对应关系Fig.11 Relationship of response of control surface and fatigue spectrum
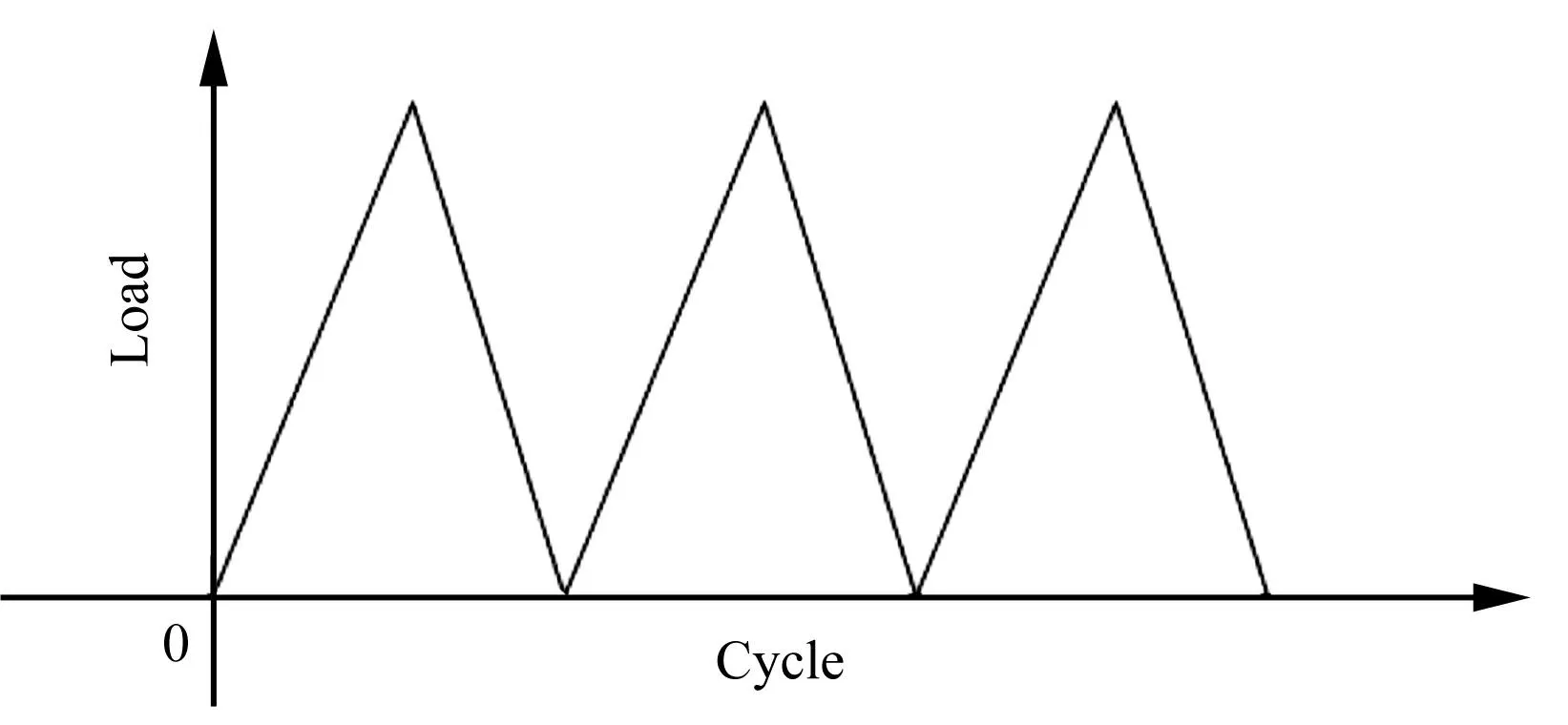
图12 疲劳载荷谱示意图Fig.12 Fatigue spectrum
4疲劳特性分析
根据线性疲劳累积损伤理论[9],在等幅载荷下,n个循环造成的损伤为:
(9)
式中:N为对应于当前载荷水平下的疲劳寿命。根据式(9)可以计算出操纵面在不同幅值的极限环振动下,对耳片所造成的疲劳损伤(见表8)。随着操纵面极限环振动幅值的增大,操纵面作动器的载荷对两端耳片造成的疲劳损伤也是不断提高的。显然,从结构疲劳安全的角度出发,只要对其周边结构造成的疲劳损伤在可以接受的范围内,就可以允许操纵面发生小幅值的极限环振动。可接受的疲劳损伤值应该与此部位由其它疲劳载荷造成的疲劳损伤值进行比对后确定。

表8 耳片的疲劳损伤
5结论
本文以一个具体的带操纵面后掠机翼为分析对象,研究了机翼操纵面系统中存在间隙极时,其飞行速
度、间隙与其所造成的操纵面作动器两端耳片的疲劳特性之间的关系。结果表明,操纵面极限环振动将引起其周边结构出现周期变化的应力,并且由于机翼气动弹性响应引起的操纵面极限环振动频率较高,因此在飞机设计寿命内将出现较大数目的载荷循环数,所以操纵面极限环振动对其周边结构所造成的疲劳损伤不容忽视。本文所发展的这一套将非线性气动弹性分析和结构疲劳特性分析相结合的分析流程,可专门用于分析操纵面极限环振动所导致的结构疲劳问题。另一方面,从疲劳强度的角度可以看到,当操纵面极限环振动的幅值较小,其所造成的疲劳损伤在可接受范围内时,允许操纵面发生较小幅值的极限环振动(这个值由对具体操纵面结构的分析得到),也不会导致其周边结构出现不可接受的疲劳损伤。这就意味着,飞机的飞行速度可以得到扩展或操纵面的实际间隙值限制可以予以放松,从而在保证飞机安全的前提下,减轻制造和维护的成本负担。
参考文献
[1]William D. Anderson, sean mortara. F-22 aeroelastic design and test validation[J]. AIAA 2007-1764.
[2]van Muijden J, Prananta B B, Veul R P G. Efficient aeroelastic simulation in a parametric procedure for fatigue aanlysis[C]. 26th International Congress of the Aeronautical Sciences,2008:14-19.
[3]贺尔铭,刘峰,胡亚琪,等.热声载荷下薄壁结构非线性振动响应分析及疲劳寿命预测[J].振动与冲击,2013,32(24):135-139.
HE Er-ming,LIU Feng,HU Ya-qi,et al.Nonlinear vibration response analysis and fatigue life prediction of a thin-walled structure under thermal-acoustic loading[J].Journal of Vibration and Shock,2013,32(24):135-139.
[4]贾尚帅,丁千,刘炜.超音速弹翼非线性颤振分析与控制[J].振动与冲击,2012,31(13):108-112.
JIA Shang-shuai,DING Qian,LIU Wei.Nonlinear flutter analysis and control of supersonic missile wings[J].Journal of Vibration and Shock,2012,31(13):108-112.
[5]de C Henshawa M J, Badcock K J,vio G A,Non-linear aeroelastic prediction for aircraft applications[J],Progress in Aerospace Sciences,2007,43:65-137.
[6]Dowell E, Edwards J, Strganac T. Nonlinear aeroelasticity[J]. Journal of Aircraft,2007,40(5):857-874.
[7]杨智春. 结构非线性颤振的理论与实验研究[D]. 西安:西北工业大学,1987.
[8]Lee I, Kim S H. Aeroelastic analysis of a flexible control surface with structural nonlinearity[J]. Journal of Aircraft, July-August, 1995, 32(4):868-847.
[9]姚卫星. 结构疲劳寿命分析[M]. 北京:国防工业出版社,2004.


