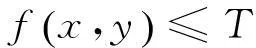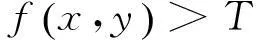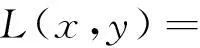长江航道主缓流判别算法研究

长江航道主缓流判别算法研究*

石磊1初秀民1▲刘潼1刘怀汉2王先登2

(1.武汉理工大学智能交通系统研究中心武汉430063；2.长江航道局武汉430014)

摘要船舶航行时充分地利用主缓流航道可以节约能源。为了更加准确地划分长江航道的主缓流航道，提出了利用k-近邻算法和P分位数法的划分方法。改进后的P分位数法采用动态选择P值的方法避免了主流区域可能过小的问题，k-近邻算法利用了测点的水深、流速等多种航道水文信息来划分主缓流。利用长江航道金口处和岳阳处的11个截面的实测数据对k-近邻算法和P分位数法进行了对比分析，其中有10个截面的主缓流区域相近。进一步对比长江航道中典型的龙口水道和杨林岩水道，发现根据算法得出的主流区宽度和实际的相比，误差在12%以内,可以满足船舶航行的需要。

关键词水路运输；主缓流分区；长江航道；k-近邻算法；P分位数法

中图分类号：U612.32文献标志码：A

收稿日期：2015-03-27修回日期：2015-04-29

基金项目*国家自然科学(批准号：61273234)、湖北省自然科学基金创新群体项目(批准号：2013CFA007)、交通运输部信息化技术研究项目(批准号：2013-364-548-200)资助

作者简介：第一石磊(1989-)，硕士研究生.研究方向：水路运输信息化技术.E-mail:331217726@qq.com

An Algorithm for Identifying Main and

Slow Flow Channels of Yangtze River

SHI Lei1CHU Xiumin1LIU Tong1LIU Huaihan2WANG Xiandeng2

(1.IntelligentTransportSystemResearchCenter,WuhanUniversityofTechnology,Wuhan430063,China;

2.ChangjiangWaterwayBureau,Wuhan430014,China)

Abstract:Vessels which navigate on the main flow channel can save energy. In order to more accurately divide the main and slow channels of the Yangtze River, this paper proposed methods of k-nearest neighbor algorithm and P-tile method. The improved P-tile method can avoid the main stream being too small by dynamic selection of P values. The k-nearest neighbor algorithm partitions the main and slow streams with channel hydrology information, such as depths and flow velocities. With the 11 sections' data of Yueyang and Jinkou measuring stations in Yangtze River, this study compared the partition results of these two algorithms. The results showed that areas of main and slow channels at the 10 out of 11 sections were close. A further comparison with the waterways at Longkou and Yanglinyan of the Yangtze River indicated the difference of the mainstream zone width estimated from the proposed algorithms was within 12% comparing to the actual, which can meet the requirements of the ship navigation.

Key words:waterway transportation; partition of main and slow stream; Yangtze River; k-nearest neighbor algorithm; P-tile method

▲通信作者：初秀民(1969-)，博士.教授.研究方向：智能交通.E-mail:chuxm@whut.edu.cn

0引言

长江是我国第一大河流，其干支流通航里程已达6.5万多km，占全国内河的52%，水运量占80%。自2005年以来，长江已经成为世界上货运量最大、运输最为繁忙的通航河流，成为名副其实的“黄金水道”。但长江航道的水流条件复杂，航行船舶为了充分的利用航道条件达到经济、节能的目的，一般船舶上行时走缓流航道，下行时走主流航道[1]。长江航道局为了能给航行船舶提供准确的主流航道和缓流航道信息，其开发的长江电子航道图3.0版新增加的功能之一就是显示航道的流速信息和主缓流区域。在电子航道图上进行主缓流分区显示，对提高电子航道图船舶终端用户航运船舶的效率、降低船舶运输成本具有重要作用。

主航道，是指供多数尺度较大的标准船舶或船队航行的航道；缓流航道，一般都靠近凸岸边滩，是指为使上行船舶能利用缓流而开辟的航道。

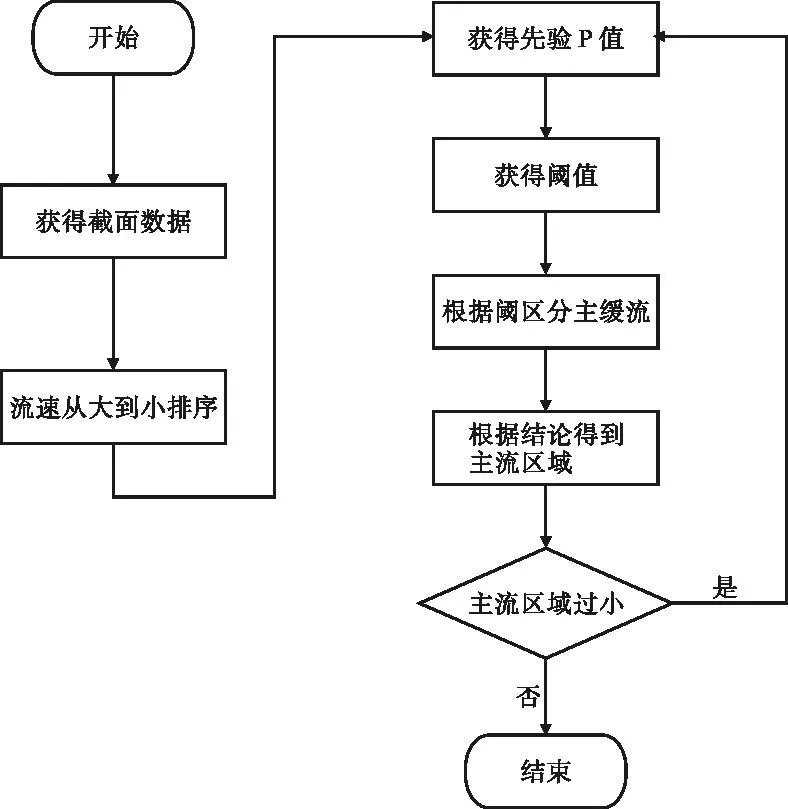
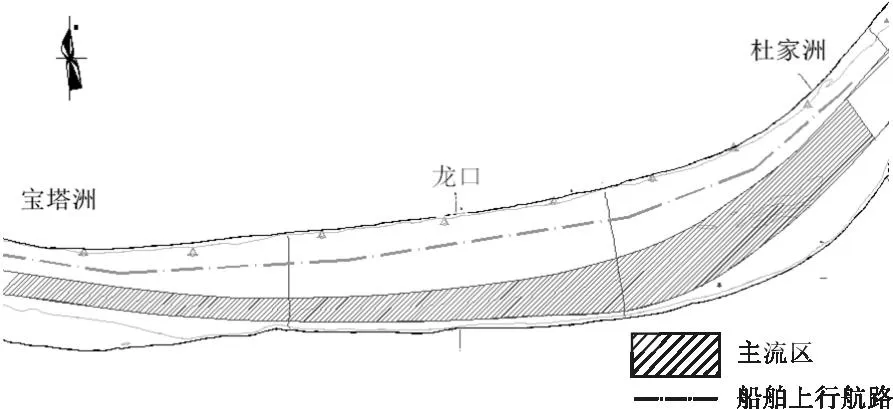
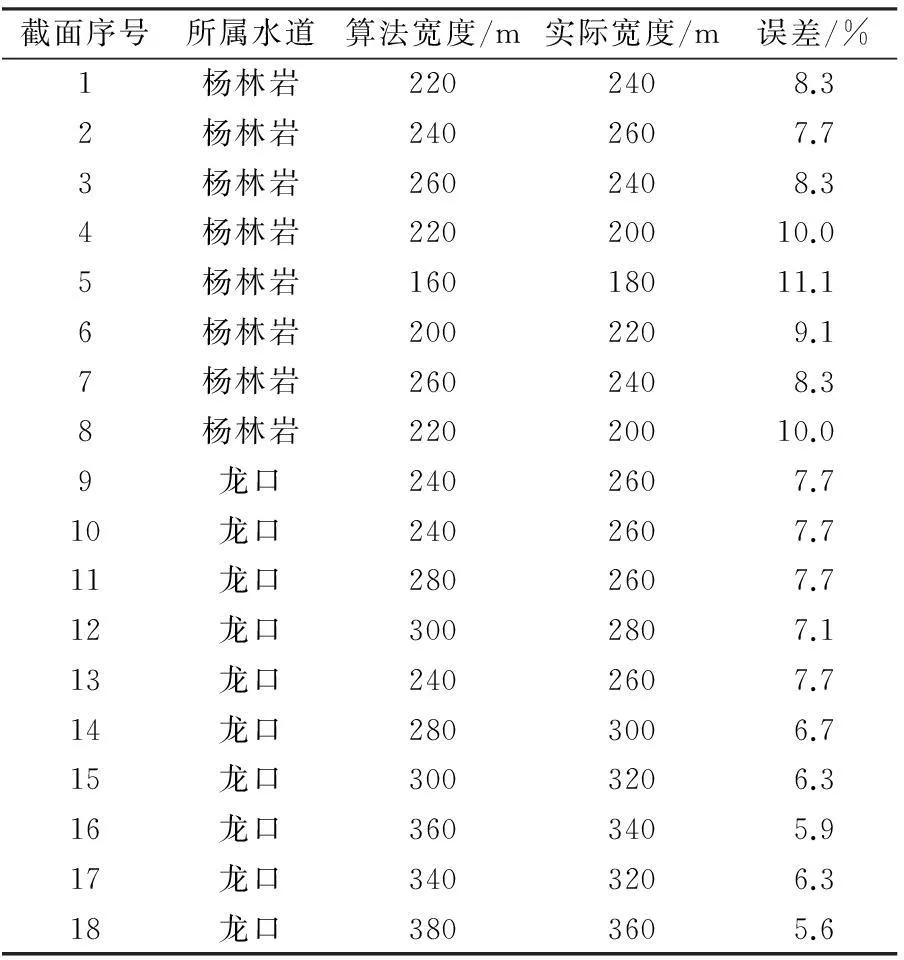
目前划分主缓流的方法主要是船舶经济航速法和P-分位数法。船舶经济航速法[2]是大多数航运企业采取的方法，其含义是根据长江上代表船型的经济航速得到主缓流分区的流速阈值。但是用该方法获得的划分主、缓流区阈值为定值。由于不同流量下的流速存在变化，如果采用该定值作为划分主、缓流区的阈值，在高流量时部分河段几乎都为主流覆盖；而在较低流量时，大部分河段会出现没有主流的情况。王先登[3]利用P分位数法对长江中游航道进行了流速区的划分，并进一步的分析了影响流速区划分的因素，但这种P分位数算法划分出来的流速区域可能过小。

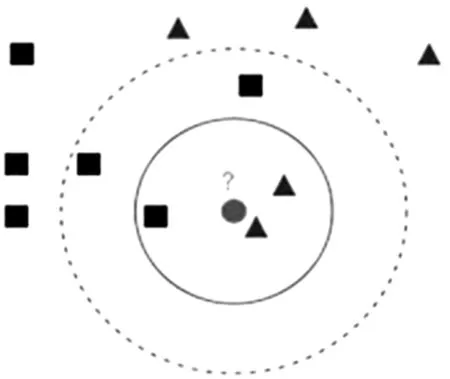
航道主缓流区域的划分可以看作1个二值化的问题。二值化是1种直接、有效的图像分割方法。通过二值化，可以将1幅图像分割为各自灰度值相似的2个区域，从而可以直观的呈现出图像中的目标和背景[4]。P分位数法是1种常见的二值化方法，简单、高效。根据航道截面数据的空间上的联系和区别，可以利用数据分类的方法对其进行划分，最后得到航道的主缓流。k-近邻算法利用数据间的空间特性能对数据进行快速的分类，是1种常用的数据分类的方法。

总的来说，目前针对长江航道主缓流分区算法的研究较少，笔者采用了k-近邻算法和P分位数法对长江航道进行主缓流分区，最终得到的结果较为符合实际，也可以满足船舶利用主缓流航道节能的需求。

1长江航道主缓流界定及分布特点

1.1长江航道主缓流界定

水力学中，天然河流通常被认为是明渠非均匀流，其特点是明渠的底坡线、水面线、总水头线彼此不平行，水深沿程变化[5]。因此，长江水流可看作是明渠非均匀流。

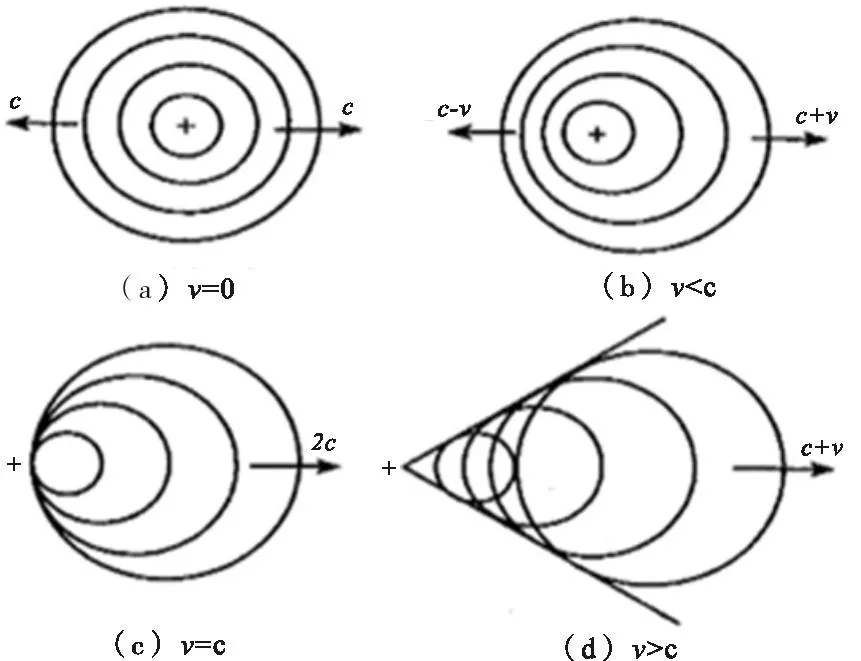
明渠水流的流态按流速大小分为急流、临界流和缓流3种[6]见图1。明渠水流的流态划分方法为

当v

当v=c，即弗劳德数Fr=1时，干扰波恰不能向上游传播，水流为临界流。

当v>c，即弗劳德数Fr>1时，干扰波不能向上游传播，水流为急流。

v-水流流速；c-干扰波在明渠静水中传播的相对波速 图1　明渠的3种流态 Fig.1　Three kinds of states of open channel flow

按上述水力学定义，经初步验算长江干线研究河段水流绝大部分都为缓流。因此，在实际的主、缓流区域划分中不能应用该定义。

天然河流中，主流指沿河流动力轴线走向的集中水流[7]。航运部门则通常把航道中表层流速较大并决定主要流向的水流称为主流。笔者研究对主、缓流的分区是为营运船舶航行服务的，所以在这里采用航运部门关于主流的概念。

由上对主流的概念，可以得到主流的以下几个特性。

1)在1个断面中主流相对流速较大。

2)主流决定水流的主要流向。

3)航道表层流速的大小决定主流位置。

因此，主流可理解为测量截面的表层流速较大且具有较大能量的测点构成的一股水流。为能够给航行船舶提供经济、可靠的主、缓流流速区域，根据航运部门对主流的概念，笔者提出了1个量化的航道主流概念：即在一定流量下一定河段中占表层流速和能量一定比例大值构成的连续的水流为主流。

1.2主缓流分布的主要特点

影响主缓流分布的因素主要有河床的平面形式、整治建筑物、浅滩、河宽、流量大小等。主缓流分布特点如下。

1)弯曲河段中，主流一般偏向凹岸。

2)分汊河段中，如2汊分流比较平均，则2段均有主流；如2汊分流比相差较大，则主流集中在1汊。

3)受浅滩或整治建筑物作用，主流也会随之变化。

4)主流一般位于深水区域。

5)在较顺直河段，主流位于河心处。

2主缓流判别算法

2.1流速测量方法

目前进行流速测量的方法主要有3种：流速仪法、浮标法和声学多普勒流速剖面仪(ADCP)[8]。

1)流速仪法。流速仪法是国内外广泛采用的测量流速的方法，同时也是衡量各种测流新方法精度的标准。常用的流速仪包括旋杯式流速仪和旋桨式流速仪。在天然河道中测量水流的速度一般采用流速仪法。流速仪测流时，首先在测流断面上设置测速垂线，然后在每条测速垂线上设测速点进行观测和计算。

2)浮标法。航道部门较常用的方法，通常由漂浮物和GPS接收机组成。该方法通过GPS接收机定位出一系列坐标轨迹及其运行时间即可求出一系列的表面流速。该方法可较好地获得水流的大体走向，但不能获取流速的最大值。该方法虽实现简单但较费工费时。

3)ADCP测流。ADCP利用多普勒效应原理，在进行流速测量的同时还能测量水深。ADCP测流分定点式和走航式2种。长江干线下临江至上巢湖河段主缓流区划分的流速测量采用的是ADCP走航式测量，测量中断面间距约为4km，部分弯道有所加密，流速点点位提取一般是间隔20m或30m。ADCP测流较快捷，断面式测量，获得高密度的流速数据。

ADCP较传统的流速测量方法具有高效、经济、快速、精确的优点，能提供流速、水深、流量、经纬度等多种截面信息，并且数据可以以文本形式导出。本文所用的长江航道金口处和岳阳处的数据就是利用ADCP测量的数据。

2.2P分位数法

P分位数法(也称P-tile法)是由Doyle在1962年提出的1种古老的阈值选取方法[9]。其原理是根据先验知识，设定目标模式与背景模式的比例(见式1)，则可根据此条件直接在模式直方图上找到合适的阈值T，使得满足式(2)的模式为目标模式，满足式(3)的模式为背景模式。

(1)

(2)

(3)

式中：p0为目标模式；pb为背景模式；T为阈值。

P分位数法是将截面的流速排序，然后按照P百分数确定阈值，从而将断面划分为主流区域和缓流区域。这种方法的关键是找到区分主缓流的阈值。

表1为长江中游航道荆州处2013年7月10日陈家湾至玉和坪河段的流速测量数据。该河段测时流量为23000m3/s，从表1可见，比例占20%时其主缓流阈值为1.63m/s；比例25%时其阈值为1.54m/s；比例30%时其阈值为1.49m/s。比例25%与30%来区分主缓流流速区差别不大，其阈值在1.50m/s左右，但如用20%作为P分位数则主流宽度偏小，该段可认为25%～30%作为P分位数较为适当。

表1　陈家湾—玉和坪河段流速信息统计

表2为长江中游航道监利河段章华港至夏家台河段测流数据，比例20%流速大值的主流在弯道和分汊段较窄，比例25%相对适中,且两者相差不大，而30%相对较宽。因此比例20%～25%的P分位数在该段确定主流较为合适。

由此可以知道，P值随着航段不同而不同，根据长江航道的流速信息统计显示，长江航道的P值可以在20%～40%之间选择。

表2　章华港—夏家台河段流速信息统计

2.3k-近邻算法

k-近邻算法根据不同特征间的距离进行分类[10]。其工作原理是：事先有1个样本数据集合，它的每1个数据都已经有标签，即样本中每1数据与所属分类的关系已经知道。当输入新的数据后，算法首先将新数据的每1个特征与样本数据对应的特征进行比较，然后根据样本中特征和新数据特征最相似的数据的所属类别将新数据分类。

图2简单的描述了k-近邻算法的分类过程，圆要被决定赋予哪个类，是三角形还是方形？如果k值取3，由于图中三角形所占比例为2/3，圆被赋予三角形那个类；如果k值取5，由于图中方形比例为3/5，因此圆被赋予方形类。

k-近邻算法的核心在于找到实例点的邻居[11]；因为在特征空间中2个实例点的距离可以反应2个实例点间的相似性程度。k-近邻算法的特征空间一般是n维实数向量空间，距离通常是欧式距离。

图2　k-近邻算法的决策过程 Fig.2　Decision-making process of k-nearest neighbors algorithm

欧氏距离是最常见的2点之间或多点之间的距离表示方法，它定义于欧几里得空间中,又称为欧几里得度量，如点x= (x1,x2,…,xn)和y= (y1,y2,…,yn)之间的距离表示为

3判别程序的实现与方法的比较

3.1判别程序的实现

3.1.1P分位数法

用P分位数法划分主缓流区域的程序见图3。但在实际的运用过程中发现得到的主流点并不是连续的，如利用P分位数法，对岳阳268点截面进行分析，P值取25%，则主缓流阈值是1.15m/s，该截面的主缓流区域的划分效果见图4。图4中带三角符号的为大于或等于阈值的点，为主流；其余为小于阈值的点，为缓流。每个数据标号的间距为20m。

图3　P分位数法判别流程 Fig.3　The flow chart of P-tile method

由图4可见，截面的主流部分并不连续，如果按照主流的含义取连续的部分，发现主流区域太小(只有60m左右)。这样的距离并不利于船舶的航行，为此需要对P-分位数法中最后的结论进行一下改进。

图4　P分位数法划分结果 Fig.4　Result of P-tile method

1)对于大于或等于阈值的点，如果其两侧的邻近连续2个点都小于阈值，则该点属于缓流；否则，该点属于主流。

2)对于小于阈值的点，如果其两侧的邻近的2个点都属于主流，则该点属于主流；否则该点属于缓流。

3)选择主流连续点最长的1段为截面的主流区域。

按照修改后的结论，对岳阳268点进行修正后的结果见图5。图5中带三角符号的为主流，其余为缓流。

图5　P分位数法划分结果(修正后) Fig.5　Result of P-tile method(revised)

3.1.2k-近邻算法

k-近邻算法在主缓流分区中的应用步骤为：

步骤1。先将流速(用S表示)和水深(用D表示)数据均一化处理，得到2组新的数据。

步骤2。将截面的数据组成1个矩阵，矩阵中的每个元素的坐标为(S,D)。其中：S,D为均一化后的数值。

步骤3。选择S较大的10%的元素作为主流矩阵；选择S较小的10%的元素作为缓流矩阵，主流矩阵和缓流矩阵同阶，而且一般为2阶或者3阶矩阵。

步骤4。按照k-近邻算法流程，这里k=3，将剩下的元素进行分类。

步骤5。在主流类中，选择流速大于平均流速而且下标连续的最长1组测量点作为该截面的主流区域；如果有多组的下标长度相等，取平均流速最大的1组。

k-近邻算法的具体流程见图6。

图6　主缓流分区中k-近邻算法的流程图 Fig.6　The flow chart of k-nearest neighbors algorithm

利用k-近邻算法对岳阳268点截面进行主缓流区域划分的结果如图7所示。图7中带三角符号的为主流，其余为缓流，每个数据标号的间距为20m。

图7　k-近邻算法划分结果 Fig.7　Result of k-nearest neighbors algorithm

3.2方法的比较

表3是用P分位数法和k-近邻算法划分同一断面主缓流的位置和宽度的统计：(当P分位数法和k-近邻算法得出的主流区域重叠的宽度大于60m时，即认为两种方法得出的主流位置相近。测点的间距为20m，P分位数法的P值为25%，k-近邻算法的k值为3。)

表3　P分位数法和k-近邻算法的分析结果

在表3中选择了金口和岳阳的11个截面进行主缓流区域的划分，可以看出通过P分位数法和k-近邻算法得出的主流位置有10个相近，2种算法得出来的主流区域的宽度有一定的差值。标号为金口29-2、金口41-2、金口50-2、金口34-1、金口51-4的截面位于金口水道铁板洲的下游，航道较为顺直；标号为岳阳232.7、岳阳240.2、岳阳247、岳阳255、岳阳276、岳阳284的截面位于城陵矶的上游，航道弯曲。将2种算法的划分结果与实际的主流区域对比发现，在金口处改进后P分位数法的结果比k-近邻算法的结果更为准确，而在岳阳处k-近邻算法的结果比改进后P分位数法的结果准确。进一步在长江干线上多个顺直水道和弯曲水道对比发现，k-近邻算法适用于弯曲航道，而改进后P分位数法更适用于顺直航道。

4算法验证

验证算法的思路是选择典型的河段，将利用算法得到的截面主流区域用柔和的曲线连接，然后与实际的主缓流区域对比。为了验证算法，选择了比较典型的龙口水道和杨林岩水道。

龙口水道是比较典型的缓流航道，因此，可以通过绘制的流速区分区与实际缓流航道设置来比较改进后P分位数法的正确性，见图8。图8中断点线为船舶上水航路，同时也是龙口缓流的大概设置范围，而2条曲线包围的区域为根据上述方法绘制的主流，其余为缓流，可见绘制缓流的范围与缓流航道的设置一致。

图8　汛期龙口水道主缓流分布图 Fig.8　Longkou waterway mainstream distribution in flood season

杨林岩水道在南明洲分汊，主流位于右汊，这与利用k-近邻算法绘制的主流一致，见图9，图9中，2曲线构成的区域为主流。杨林岩和龙口水道的测量截面间距为0.5～1km，其中杨林岩水道有8个测量截面，龙口水道有10个测量截面。算法的分区结果与实际的主流区宽度的误差在12%以内，见表4。截面的水文条件、航道的地形条件以及航道周围的水工建筑等都会影响主缓流区域的划分，P分位数法和k-近邻算法不能完全的符合航道的条件，所以算法的结果存在一定的误差。

图9　枯水期杨林岩水道主流分布图 Fig.9　Yanglinyan waterway mainstream distribution in dry season

截面序号所属水道算法宽度/m实际宽度/m误差/%1杨林岩2202408.32杨林岩2402607.73杨林岩2602408.34杨林岩22020010.05杨林岩16018011.16杨林岩2002209.17杨林岩2602408.38杨林岩22020010.09龙口2402607.710龙口2402607.711龙口2802607.712龙口3002807.113龙口2402607.714龙口2803006.715龙口3003206.316龙口3603405.917龙口3403206.318龙口3803605.6

5结束语

长江航道主缓流分区是典型的二值化和数据分类问题，P分位数法和k-近邻算法能很好的解决这一类问题。考虑到航道主流区域的连续性，可以对P分位数法得出的主流点的邻近点进一步分析，这样得到主流区域比较合理；考虑到P分位数法仅仅利用了流速信息，提出了利用k-近邻算法进行主缓流判别的程序，利用流速和水深等多种信息对测量点进行分类。k-近邻算法和P分位数主缓流分区结果相似表明了算法理论上的正确性，其中k-近邻算法适用于弯曲航道，P分位数算法更适用于顺直航道。算法在龙口水道和杨林岩水道实际应用的结果表明，利用算法划分的主缓流区与实际的情况比较符合。但是在比较特殊的河段，如两坝间及近坝下水域、感潮河段、支流河口等，需要对算法做进一步的研究。

参考文献

[1] 熊焱斌. 浅析长江轨道限速规定[J]. 中国水运：下半月，2013,13(2):3-4.

XIONG Yanbin. Analysis of the Yangtze River waterway speed limit[J]. China Water Transport: The Second Half, 2013, 13(2):3-4.(in Chinese)

[2]张署.船舶营运航速的优化分析[D].上海：上海海事大学,2004.

ZHANG Shu. Optimization analyses of ship operating speed [D]. Shanghai:Shanghai Maritime University, 2004. (in Chinese)

[3]王先登. 长江中游航道流速区划分及影响因素研究[J]. 水运工程,2014，56(9):115-120，125.

WANG Xiandeng. Division method and influential factors of waterway flow velocity area in the middle Yangtze River[J].Port & Waterway Engineering, 2014，56(9): 115-120. (in Chinese)

[4]王刚.图像二值化方法研究及其在监控识别系统中的应用[D].长沙：湖南大学,2010.

WANG Gang. Research on image binarization algorithm and its application in surveillance recognition system [D]. Changsha:Hunan University, 2010. (in Chinese)

[5]林劲松,巨江,张宽地. 复杂地形条件下天然河道水面线计算研究[J]. 西北农林科技大学学报：自然科学版),2010，38(9):187-191.

LIN Jinsong, JU Jiang,ZHANG Kuandi. Under the condition of complex topography on the natural water surface line calculation study[J]. Journal of Northwest Agriculture and Forestry University of Science and Technology Journal:Natural Science Edition, 2010,38(9):187-191.( in Chinese)

[6]丁磊,张庆河.光滑壁面明渠水流的三维格子玻耳兹曼模拟[J]. 天津大学学报,2011，44(2):120-125.

DING Lei, ZHANG Qinghe. Simulation of smooth open channel flow by 3D lattice boltzmann method [J]. Journal of Tianjin University, 2011，44(2):120-125. (in Chinese)

[7]覃莲超,余明辉,谈广鸣. 河湾水流动力轴线变化与切滩撇弯关系研究[J]. 水动力学研究与进展A辑,2009，24(1):29-35.

QIN Lianchao, YU Minghui, TAN Guangming. Discussion on the relation between the change of the flow dynamic axis and the bend bypassing and shoal cutting in the bend river course [J]. Water Dynamics Research and Progress in A Series, 2009，24(1):29-35.(in Chinese)

[8]饶西平. ADCP测流与传统测流的对比及应用[J]. 科技资讯,2012，29(6):96.

RAO Xiping. The comparison and application of ADCP and traditional velocity measurement [J]. Information of Science and Technology, 2012，29(6):96. (in Chinese)

[9]陈冬岚,刘京南,余玲玲. 几种图像分割阈值选取方法的比较与研究[J]. 机械制造与自动化,2003，21(1):77-80.

CHEN Donglan, LIU Jingnan, YU Lingling. Comparison of image segmentation thresholding method [J]. Journal of Mechanical Manufacturing and Automation, 2003，21(1):77-80. (in Chinese)

[10] KHEDR. A M. Learning K-nearest neighbors classifier from distributed data[J].Computing and Informatics, 2008,27(3):52-56.

[11]谢海红,戴许昊,齐远. 短时交通流预测的改进K近邻算法[J]. 交通运输工程学报,2014，14(3):87-94.

XIE Haihong, DAI Xuhao, QI Yuan. Improved k-nearest neighbor algorithm for short-term traffic flow forecasting[J]. Journal of Transportation Engineering, 2014，14(3):87-94. (in Chinese)