基于Snake模型的建筑物群移位算法改进研究

基于Snake模型的建筑物群移位算法改进研究

杨莉

(湖北省国土测绘院，湖北武汉430010)

摘要：在对Snake模型研究的基础上，结合建筑物群在移位中的特点，从2个方面对Snake模型进行改进：首先，在Snake模型中加强对齐排列建筑物群这一重要空间特征的识别，以便保持对齐排列建筑物群在移位前后不变；其次，针对传统Snake模型有时无法解决两个建筑物空间冲突的缺点，对街区中的建筑物群实行分层次移位，先将有冲突的两个建筑物作为整体，与剩余其它建筑物利用Snake模型一起移位，然后再根据文中提出的建筑物间相互冲突的4种受力模型，进行建筑物间空间冲突的移位。最后利用改进的Snake模型进行移位实验和分析。

关键词：Snake模型；建筑物群；空间关系；受力模型

中图分类号：P208

收稿日期：2014-05-15

作者简介：杨莉(1988-)，女，工程师，硕士.

ResearchontheimprovedapproachforbuildingclusterdisplacementbasedonSnakemodel

YANGLi

(LandsurveyingandMappingInstituteofHubeiProvince，Wuhan430010，China)

Abstract：Based on the research of snake model，it presents two improvements on snake model applied to the building cluster displacement.Firstly，in order to protect the important spatial relationship，buildings alignment，a method that strengthens the identification of alignment is proposed to maintain the spatial relationships in the displacement.Secondly，against the weakness of snake model that can not solve the conflicts between buildings，hierarchical displacement of buildings cluster is implemented to improve the computer method of conflict force between buildings，and fourth force models are proposed to displace buildings in conflict with other buildings.Finally，the improvement snake model is used in displacement experiment and the result is analyzed.

Keywords：Snakemodel；buildingcluster；spacerelationship；forcemodel

各种专题地理信息系统的建设越来越受到重视[1]，作为产生基础地理信息的地图综合也有着重要的研究意义。在地图综合中，由于比例尺缩小，地图要素符号的相对扩大，造成地图要素之间产生空间冲突。为了保持地图的清晰性，必须处理这些冲突。在处理空间冲突的地图综合算子中，移位算子是解决冲突，保持要素之间空间关系的主要方法。建筑物群的空间冲突解决则是地图综合中移位研究的一个重要方面。

目前，国内外众多学者已对建筑物群的移位算法进行了研究[2-11]。其中Snake模型是典型的解决冲突的方法，最初应用于线要素移位[12]。然而，Snake模型在建筑物群移位中有些许不足，如无法较好的识别和保持呈对齐排列的建筑物群的空间关系；无法较好解决Snake内部自身的空间冲突，即建筑物之间的冲突。本文在Snake算法研究的基础上，对其进行改进，最后利用改进的Snake模型进行建筑物群的移位，取得较好的效果。

1Snake模型简介

Snake模型是能量最小化方法，将要素的几何特征变化作为内部能量，外部空间冲突作为外部能量，通过微分方程求解得到总能量最小时的矩阵方程，K·D=F，再利用有限元方法对矩阵方程求解，得到移位后的形状和位置[12]。其中，K为刚度矩阵，F为单元的受力矩阵，D为在受力矩阵F的作用下，线段首末端点的移位量和一阶导数变化。Snake模型将力分为x和y两个方向分别来求解，分别求得x，y方向的移位量，最后把x和y方向的移位量进行合成得到每个点的真实移位量。

本文在应用Snake算法进行建筑物移位时，同文献[12]中一样，将街区中的建筑物群用重心表示，用最小生成树连接所有建筑物的重心，然后进行整体移位，保持建筑物群的空间关系。

2Snake模型改进

2.1　对齐排列建筑物群识别的改进

地图综合中，成对齐分布的建筑物群很容易被人眼识别，需要在制图综合中加以保护，保证移位前后建筑物群的空间排列关系不变。文献[12]中曾提出一种判别建筑物群成对齐分布的方法，但是存在较容易判别失误及建筑物的方向计算有局限性的缺点。本文利用格式塔中的一些原则进行改进。

格式塔原理最开始应用于心理学，它主要指人们在视觉判断和识别的时候，会不自觉的受到一些规则和约束的影响，它包括接近性原则、相似性原则、连续性原则和完整性原则等。而对齐排列建筑物群也遵循着格式塔的规律，在其内部每个建筑物大体相似，且相互间距离接近。因此，本文利用格式塔原理中的接近性原则和相似性原则来识别呈对齐排列的建筑物群。在算法中，接近性原则用两个建筑物间的欧式距离d表示，相似性原则用两个建筑物间的面积大小差异Ws和方向差异Wd表示；然后将Wd和Ws分别作为权值加载到距离d上，获取两个建筑物间的亲近度f，

(1)

其中，f越小，建筑物间关系越亲密；f越大，建筑物间关系越疏远，若几个建筑物间比较亲密，且亲近度f差不多大，则认为它们属于同一个对齐排列的建筑物群。

通过实验，确定Wd对应的角度变化为[0，90o]，设Wd权值变化为从1到2，角度差值越大，权值Wd越大。单个建筑物的角度计算如图1所示，做多边形的最小面积外接矩形(对凹多边形而言，要先做凸壳，再做最小面积外接矩形)，再计算该外接矩形的长轴方向(长轴是指连接矩形各边中点的连线中，最长的那条线，以长轴与平面坐标系中x轴方向的夹角(0~90o)作为建筑物的方向角度)作为角度大小。

图1　建筑物的方向

用Ws表示两个建筑物间的面积大小差异权值，用两个建筑物的面积比表示(面积小的多边形比面积大的多边形)。同理，参数Ws的范围也是根据实验后确定的。面积比的范围为[0,1]，设Ws的权值范围为[0,2]，面积比越小，权值越大，两个建筑物的面积差异越悬殊。强制在面积比小于0.25时，权值Ws为2。

根据式(1)，得到结果，如图2和表1所示。从表1中发现线段17的亲近度特别小，因为线段17连接的两个建筑物在图上存在空间冲突，因此它们之间的实际距离较其它要小很多(同时，若探测到建筑物之间存在压盖冲突，即它们之间实际距离为0，则在程序实现时，强行设定它们间的距离为0.001m)。因此，将线段17连接的两个建筑物先提取出来。同时，在剩余的亲近度中，线段8,9,10的亲近度是最小的，且相互之间比较相近，可以识别出它们连接的建筑物属于对齐排列的建筑物群。

图2　每条连接边的权重值

找到对齐排列的建筑物群和有冲突的建筑物后，做它们的凸壳，如图3所示，图中阴影部分为凸壳。将凸壳与其它剩余建筑物一起，在Snake模型下移位，当它们最后移动到合理的位置后，记下凸壳的移位量，然后将这个移位量加到每一个组成其凸壳的建筑物中，这样，组成对齐建筑物群的每一个建筑物移位量都相同，保证凸壳内部之间的空间关系不变。同时，对图3中的凸壳1而言，凸壳内部的建筑物之间是有冲突的，需要在内部对冲突建筑物进行调整。

2.2　建筑物之间受力模型的改进

在用传统Snake模型进行建筑物移位时，建筑物之间冲突的受力计算与建筑物与道路冲突的受力计算方法是不同的，建筑物之间是用缓冲区计算受力，而建筑物与道路之间是用距离计算受力[12]。这两种不同的计算方式所得数值在数量级上相差很大，当同时存在着两种冲突时，有时不易解决建筑物内部的冲突。如图4(a)所示，建筑物A、B、C通过最小生成树相连，其中建筑物A与街道有冲突，建筑物B与C之间有冲突。在移位中，由于Fa>Fb，会促使着建筑物B向C的方向移动，造成移位后建筑物B与C仍然冲突的局面，如图4(b)所示。

图4　建筑物内部冲突移位后仍然存在

为了解决这个问题，将建筑物群实行分层次移位。先将相互间有冲突的建筑物整体移位，然后根据四种冲突模型，分别进行调整，解决建筑物之间的冲突。先设定要素间的所需最小距离值为0.2mm(即人眼在地图上可分辨的最小距离)。

建筑物之间的冲突分两种，一种是符号之间距离太近，在视觉上出现拥挤而产生的邻近冲突，如图5(a)所示。每个建筑物在地图上占据一定大小的空间，面积越大，移动时对周围要素的影响越大，基于此，本文在移位时考虑建筑物的面积因素，面积大小与移位量成反比。随后分别做两个建筑物宽度为0.1mm的缓冲区，这两个缓冲区相交于点P1，P2，连接P1P2，垂直于P1P2指向B1的方向，同理，V2为建筑物B2的受力方向。

(2)

另一种是建筑物之间互相压盖产生的空间冲突，如图5(b)、5(c)、5(d)所示。压盖方式不同，受力分析也不同。依据符号压盖产生的相交线的中点来判断不同压盖方式。

图5(b)为相交连线P1P2的中点P在相交多边形内部的情况。冲突解决方案为式(3)。对建筑物B1而言，找出既在B1边界也在相交多边形(图中阴影部分)边界上，且距离连线P1P2最远的点F1，记距离为dmax1，同理，找出建筑物B2的点F2及距离dmax2。点F1到连线P1P2方向的垂线向量V1为B1的受力方向；点F2到连线P1P2方向的垂线向量V2为B2的受力方向。

(3)

图5(c)为相交连线P1P2的中点P在相交多边形边界上的情况，冲突解决方案为式(4)。找到相交多边形(图中阴影部分)边界上距离连线P1P2最远的点，计算到连线的距离dmax，两个建筑物的受力大小分别为F(B1)，F(B2)；垂直于连线P1P2指向B1的方向，同理，V2为建筑物B2的受力方向。

(4)

图5(d)为符号相交连线P1P2的中点P在相交多边形外部的情况，冲突解决方案为式(5)。在相交多边形(图中阴影部分)中找到离连线P1P2距离最大的点，作最远点到连线的垂线，然后取垂线在相交多边形中的部分，计算它的长度，记为dmax，两个建筑物的受力大小分别为F(B1)，F(B2)；其方向同上面一样。

(5)

第二种压盖冲突的建筑物经过上面移位后，符号之间已移开，没有了压盖，但相互间距离太小，仍然存在第一种邻近冲突，但它们之间的受力模型已变为图5(a)的类型。因此，还需要再利用第一种受力模型中的方法对建筑物进行后续移位，方可最终解决空间冲突。

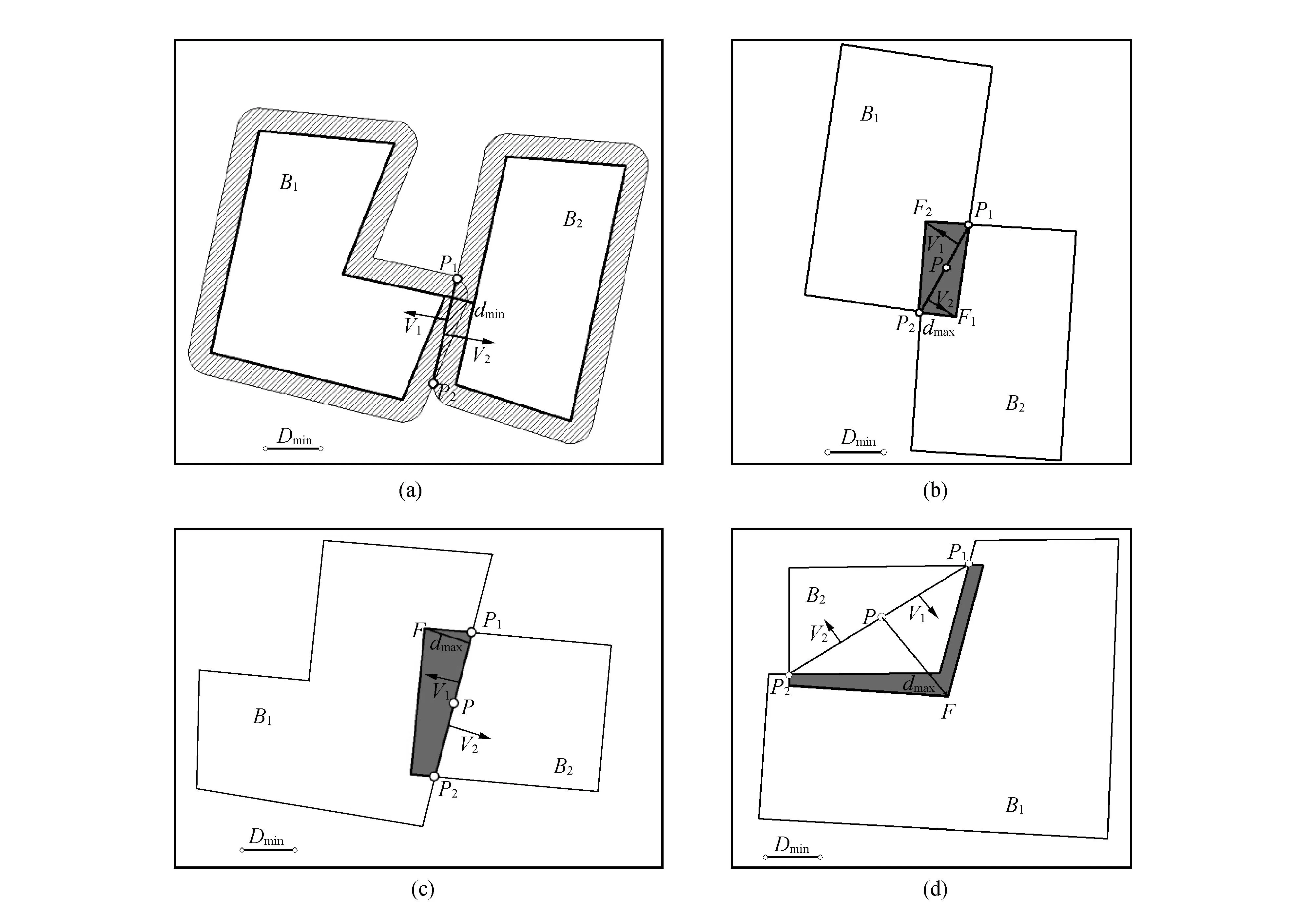
图5　建筑物之间的四种受力模型

3实验与分析

图6是应用改进的Snake模型对某地区建筑物群进行移位的示例图，图上最小可识别距离为0.2mm。图6 (a)是移位前的情况，图6(b)是移位后的情况。从图6中可以看到，大部分冲突在移位后解决的比较好，并且建筑物相互间的冲突通过移位后得到了解决，空间拓扑关系也保持的很好，街区内的重要的空间拓扑关系，如对齐排列的建筑物，移位后的相互空间关系也没有被破坏。

4结束语

通过实验可以看到，在建筑物群移位算子中应用改进后的Snake算法，总体上可以满足制图综合的需要，但也存在问题需要进一步的解决。一是在移位区域不充裕时如何移位，既要满足建筑物与道路冲突的解决，也不能与其它建筑物之间产生冲突，这可能需要建筑物适当的变形；二是Snake算法本身参数的不好确定，Snake算法的两个形状参数α，β在不同比例尺、不同受力大小下的值都不一样，现在需要人为确定，并没有一个统一的模型设定准确的值。

参考文献：

[1]周炤，肖强，赵国成，等.基础地理空间数据持续更新模式分析[J].测绘工程，2014,23(1)：12-16.

[2]刘小春，华一新，郑刚，等.面向服务的分级地理空间数据中心框架的构建[J].测绘工程，2014,23(1)：57-60.

[3]赵军喜，孙庆辉，张亚军.地理空间元数据理论体系研究[J].测绘工程，2014,23(4)：10-13.

[4]费立凡，河津.解决街道与建筑物图形冲突的移位模型研究[J].武汉大学学报:信息科学版，2007,32(6)：540-543.

[5]WAREJM，JONESC.B.ConflictReductioninMapGeneralizationUsingIterativeImprovement[J].GeoInformatica,1998,2(4):383-407.

[6]WAREJM，JONESCB.AutomatedMapGeneralizationwithMultipleOperators：ASimulatedAnnealingApproach[J].GeographicalInformationScience，2003,17(8):743-769.

[7]LONERGANME，JONESCB.AnIterativeDisplacementMethodforConflictResolutioninMapGeneralization[J].Algorithmica,2001,30,287-301.

[8]WILSONID，WAREJM，WAREJA.AGeneticAlgorithmApproachtoCartographicMapGeneralization[J].ComputersinIndustry,2003,52,291-304.

[9]艾廷华.基于场论分析的建筑物群的移位[J].测绘学报，2004,33(1)：89-94.

[10]HOJHOLTP.SolvingSpaceConflictsinMapGeneralization：UsingaFiniteElementMethod[J].CartographyandGeographicInformationScience，2000,27(1)：65-73.

[11]吴小芳，杜清运，徐智勇.多层次移位原则的道路与建筑物空间冲突处理[J].测绘学报，2010，39(6)，649-654.

[12]BADERM.EnergyMinimizationMethodsforFeatureDisplacementinMapGeneralization[D].Zurich：DepartmentofGeography，UniversityofZurich，2001:138-143.

[责任编辑：李铭娜]