基于KMV模型的地方政府债券违约风险测度
基于KMV模型的地方政府债券违约风险测度
贾智莲,王宙翔
(内蒙古财经大学财政税务学院,内蒙古呼和浩特010070)
[摘要]新预算法实施后,地方政府债务取得合法地位,地方政府债券风险的控制显得尤为重要。本文以内蒙古自治区为例,运用KMV模型对2015-2017年地方政府债券违约风险进行了测度,并预测了内蒙古自治区安全的地方政府发债规模。研究结果表明,内蒙古自治区2015年和2016年政府债务存在违约风险,2017年不存在违约风险。并且,内蒙古自治区三年期、五年期和七年期的发债规模控制在当年财政收入的10.40%、8.96%和8.38%之内时,将不会产生违约风险。
[关键词]地方政府债券;债务规模;违约风险
[收稿日期]2015-05-15
[作者简介]贾智莲(1972-),女,内蒙古巴彦淖尔人,内蒙古财经大学财政税务学院教授,博士,从事地方财政理论与制度设计研究.
[中图分类号]F812.7[文献标识码]A
一、引言
我国的地方政府债务制度起步比较晚。1994年颁布的《预算法》第28条明确规定“除法律和国务院另有规定外,地方政府不得发行地方政府债券”, 这一规定原则上禁止了地方债的存在。但是1994年分税制改革造成的财权与支出责任不匹配,地方税体系不健全等问题直接导致了地方财政失衡。与此同时,地方政府在加快地方基础设施建设,促进地方经济发展,保障民生和加速城镇化建设中承担的责任越来越大,导致地方政府财政压力不断增大。在地方财政失衡的大背景下,针对地方债的禁令催生了地方政府的各类博弈行为。虽然原《预算法》禁止地方发债,却留有制度漏洞,没有对地方政府的融资行为进行有效的约束与监督。因此,地方政府通过各类融资平台来间接发债,而中央政府则选择性地忽视了地方政府这一行为。在这种“默契”之下,地方债愈演愈烈,甚至危及财政的可持续恶性发展。根据审计署2013年底发布的全国政府性债务审计结果, 截至2013年6月,地方债务总额为178908.7亿元,占当年GDP的30%以上。这种“掩耳盗铃”式的做法使大量地方债务游离于法律控制之外,并无法在预算中得到准确反映,从而脱离上级政府与同级权力机关的监督,加剧了财政风险。
事实上,地方债并非洪水猛兽。政府债券是国际通行的地方政府融资方式。大多数发达市场经济国家都允许地方政府举债。只要能够确保地方政府举债行为规范有序,地方债不仅可以成为开辟地方财源的有效途径,还可以实现公共品成本分摊的代际公平。实践中,我国多次尝试突破修改前《预算法》的规定,进行地方政府发债的探索。1998年,为了应对亚洲金融危机,通过转贷国债的方式进行了初步尝试。2008年底,中央为了刺激经济,制定了四万亿的投资计划,为了解决地方政府配套资金,中央通过特别方式允许发行地方政府债券,这是城投债的起步。2009年,由于相关政策的扶持,城投债大量的增长,我国的地方政府债券进入了代发带还的阶段。2011年,中央批准深圳、上海等四地市作为试点,自行发债,由财政部还本付息,在此之后又增加了山东和江苏为试点,进入地方政府债券的自发代还的阶段。2014年,中央批准10 个省市自己发行地方政府债券。
直到2014年8月,《预算法》修订终于尘埃落定,新《预算法》的一个重大突破就是允许省级地方政府在国务院确定的限额内,通过发行地方政府债券融资。至此,地方政府“隐形”发债权终于从幕后走到台前,接受政府预算的规范和约束。紧接着,2014年10月2日,国务院出台《关于加强地方政府性债务管理的意见》(国发(2014)43号)文件,对地方债务管理做出了明确的规定,以建立“借、用、还”相统一的地方政府性债务管理机制,有效发挥地方政府规范举债的积极作用,切实防范化解财政金融风险。进入2015年后,中央财政连续出台了一系列规范地方政府债务发行的制度。3月16日,财政部发布《地方政府一般债券发行管理暂行办法》,4月7日,发布《地方政府专项债券发行管理暂行办法》, 5月12日,由财政部、中国人民银行和银监会联合发布《关于2015年采用定向承销方式发行地方政府债券有关事宜的通知》,等等,由此看出,地方政府债务取得了合法的地位之后,对地方政府债务风险的控制变得非常迫切和重要。只有规范地方政府的举债行为,控制地方政府债券的发行规模,合理用债偿债,才能最大限度地发挥地方债对地方经济社会发展的助力作用。
二、文献综述
针对地方债务风险问题,国内学者做了大量的研究。丛树海等(2004)通过对财政风险的影响程度不同,从财政内部风险和财政外部风险中选取了20个核心指标,构建了一个财政风险预警系统。运用指数预警方法,对各指标进行了指数化分析,设定了各指标的警戒线,以此来分析风险状况。接着,选取了1990-2001的相关数据,代入到预警系统中,并经过周期分析,得出的结论是,在样本期内,我国的财政风险未超过所设定的警戒线。李昊(2010)构建了地方政府债务风险预警的指标体系,并通过10位专家对指标体系中的18个指标进行打分,划分了风险级次。他先是经过因子分析法,对指标进行了处理,运用了fisher判别分析法构建了适合于小样本量的债务风险预警模型,通过运用多层感知器神经网络构建了适合于大样本的债务风险预警模型,并与专家打分值进行了拟合,发现二者高度保持一致。最后运用Repast Simphony构建了单个地方政府和多个地方联动的债务风险动态预警模型,对地方政府债务进行分析。周青(2011)构建了地方投融资平台风险指标体系,运用模糊综合评价的方法和层次分析法,分析了投融资平台的债务风险。并且,他为了度量投融资平台融资风险,在运用Credit Metric模型时考虑了我国的国情,认为地方政府融资平台降低信用等级的可能性的概率要比一般的公司概率小,所以在原有的模型中加入了乘数因子,对融资风险做了一维的度量。洪源等(2012)借鉴了粗糙集和BP神经网络评估系统,构建了地方政府债务信用风险非线性仿真预警系统,这样就下降了BP神经网络评估系统的复杂性,并且具有很好的信用风险预警准确性。
韩立岩等(2003)参考了美国市政债券的发行概况,利用KMV模型构建了地方债券信用风险模型,提出了计算理论违约概率的方法。他指出:财政收入相对于企业的净资产市值,是偿还到期债务的主要保障。但财政收入中一部分是用来满足地方政府自发性支出,剩余的财政收入才可以偿还到期债务,其中剩余的这部分财政收入被称为担保收入。在担保收入的确定上,他们运用了两种方法。一种是观察财政支出的走势图,然后将最近的一个阶段的地方财政支出均值作为自发性财政支出。另一种是构建滑动财政支出模型,然后将常数项确定为自发性财政支出。他利用北京与上海的相关数据,通过连续试算,分析了不同发债规模下的信用风险,得出理论违约概率。韩立岩等(2005)研究了市政债券信用风险的识别原则和测量方法,运用模糊期权方法,分别考虑了财政收入服从对数正态分布和真实正态分布的情况下北京和上海的违约概率和安全的发债规模。最后还结合了美国和日本市政债券风险控制模式,对我国的市政债券的风险防范给出了政策性建议。茹涛(2009)运用了KMV模型对上海市的安全规模进行了测度。预测财政收入时,他构建了一阶自回归模型,对上海市2009年的财政收入进行了预测。在担保收入的确定上,他是把基本建设拨款、企业技术改造投资这部分财政支出确定为担保收入。卢小曼(2011)用KMV模型,对我国30个省、直辖市进行了安全规模的测度。接着,又与2009年和2010年各个地方实际发债规模相比较,得出的结论是不同地区的风险差异比较大。东部地区的安全发债规模较大,2010年的违约风险也比较小,中部和西部的安全发债规模则相对较小,并且,西部地区2010年存在着违约的风险。李腊生(2013)在分析债务风险时,结合了我国的国情,考虑了地方政府债务可以向中央转移。他讨论了债务可转移性和转移途径,改进了KMV模型,加入了中央政府承接地方政府债务的最大承受能力变量,对全国18个省市的违约风险进行了分析。最后得出结果为,我国地方政府不存在经济上违约风险,而存在道德风险。马德功等(2015)考虑了我国的国情,借鉴了李腊生(2013)的KMV模型,对四川省2013和2014年债券到期债务进行了推算,运用KMV模型,计算出了相应的违约距离和违约概率,得出的结论是四川省2013年和2014年不会出现违约风险。接着,他又运用了改进的KMV模型,通过对2013年和2014年四川省地方政府债务压力测试,推算了四川省2013和2014年三年期和五年期的债券违约概率和安全的发债规模。李江波(2010)在原有的KMV模型中加入了Knight因子,也就是Knight不确定性。通过对KMV模型的改进,得到了Knight不确定下测度地方政府债券信用风险的模型。改进后的KMV模型中违约点、公司的市场价格及其波动率的计算方法与原来的KMV模型一样,但在违约距离与违约概率的计算上就有所不同,他引入了Knight因子λ,揭示了除信用风险之外的不确定性。他选取了北京市1978-2009年的相关数据,进行了信用风险的分析,测度出北京市的安全发债规模,并且计算了不同λ值下的违约距离和违约概率。得出的结论是,加入λ的情况下,违约概率将变成一个区间,不再是一个定值,并且,当λ>0时,随着λ增大,违约概率区间也将会越来越大。马亭玉等(2012)从地方政府债券信用利差的角度分析了债务规模对信用风险的影响。他们构建了回归模型,得出的结论是,地方政府债务的信用风险溢价对发债规模有一定的敏感度。然后又运用引入Knight因子的KNV模型,测度了四个省市的安全发债规模。可以看出,在对地方政府债务风险研究的研究中,债务规模是一个影响债务风险的重要变量。
三、信用风险评价的方法
信用风险评价在资本市场上很早就有提出,经济学家们也提出了很多相关的方法和模型。大致可以分为以下几类:
(一)5C要素分析法
5C要素分析法是资本市场上对借款人信用风险分析的一种方法。它主要是通过对每一个考察的要素量化、评分,确定借款人的信用等级。5C要素包括道德品质(Character)、还款能力(Capacity)、资本实力(Capital)、担保(Collateral)和经营环境条件(Condition)这些要素。不同的金融机构有不同的要素指标。有的机构注重5W要素,包括借款人(Who)、借款用途(Why)、还款期限(When)、担保物(What)及如何还款(How)。还有的是5P要素,有个人因素(Personal)、借款目的(Purpose)、偿还(Payment)、保障(Protection)和前景(Perspective)。
(二)财务比率分析法
财务指标一直是分析借款人的重要参考。财务比率法是将各类财务指标作为一个整体,全面的反应借款人的信用状况。具有代表性的就是杜邦分析法和沃尔比重评分法。前者是将净资产利润率作为核心,具有先创性的将净资产利润率分解为不同层次的指标,用来判断借款人的财务状况。与它不同的是,后者先是设定一些财务指标,并分别给各指标分数权重,然后通过与标准比率或行业平均比率比较,确定各指标得分以及总体累计得分,以此来判断借款人的信用等级。
(三)多变量统计方法
多变量统计方法主要是以财务比率为重要指标,运用统计的方法而建立起来的标准模型。其主要包括:多元判别分析法、Logit模型、非参数法和数学规划法。其中多元判别分析法要求服从正态分布以及等协方差的特征,并且不同组样本存在重叠时多元判别分析法和Logit分析容易产生误判。由于现实样本具有不能都满足正态分布等现实意义,所以,非参数法和数学规划法成为研究的方向。
非参数法主要的分析方法是聚类分析。聚类分析是模拟了自然界的“物以类聚,人以群分”的现象,将不同的变量进行分类,用聚类变量描述对象的特征。它假定每一类都有一个中心,代表所有属于该类的都应该拥有的共性,将与中心最相似的变量归为一类。这在信用风险评价中,可将不同贷款人分类,债权人可以对不同的债务人采取不同的贷款策略。而数学规划方法是运用数学规划方法解决信用N类分类的问题,建立规划方程,来对信用风险的预测。
(四)人工智能方法
随着计算机和其他学科的发展,人工智能的分析方法也产生了。主要包括:信用评估专家系统、神经网络评估系统和粗糙集方法。信用评估专家系统是运用了计算机技术,将专家的信用评估经验编入程序,用计算机来进行信用评估。神经网络评估系统是借鉴生理学上的人脑神经网络的知识,模拟出的一种信息处理系统,不要求样本数据服从某一分布,具有非线性映射能力和泛化能力,所以具有比较高的预测精度。与前两种不同的是,粗糙集方法可以有效地分析不精确、不一致、不完整等各种随机、不确定信息,其核心是从近似空间中导出的上近似算子和下近似算子,从而制定出粗糙集代数系统,来判断信用风险。
(五)以资本市场理论为基础的计量模型
由于资本市场的不断发展,金融工具不断地创新,相关的信用风险也就变得越来越复杂。所以,一系列新的信用风险衡量方法出现了。主要包括:Credit Metrics、CreditRisk+、KMV模型、CreditPortfolio View方法。这些模型和方法都是基于一定的资本市场理论来确定借款人的信用风险的可能性。其中KMV模型就是运用期权定价理论为基础,通过企业净资产市值和负债规模来计算借款人的预期违约距离和违约概率,判断信用风险的可能性。
通过对各种方法和模型的优缺点进行系统的分析和对比,并考虑对政府债务研究的适用性,本文选择KMV模型对地方政府债务风险进行评价与测度。
四、KMV模型的技术说明
(一)KMV模型基本思想的构建和计算过程
KMV模型也称为信用风险的期权定价模型,主要是为了计算公司的预期违约概率 EDF(Expected Default Frequency),所以又被称作是EDF模型。该模型认为,企业对外借取债务,就相当于把企业的所有权先让渡给债权人。如果债务到期时,企业的净资产市值超过债务,就可以从债权人手中赎回所有权,债权人就可以获得利息和收回本金;如果企业的净资产市值低于到期债务总额,企业就会违约,即债权人遭受损失。
从期权定价理论的角度来看,上述的二者的损益是等价的(Merton,1974)。公司的债务可以看作是以公司资产为基础的一种看涨期权。具体来讲是,对于一个上市公司来说,假设它有股权和负债,在债务到期时,如果公司的净资产小于债务,资不抵债,股东就会放弃公司的所有权,出现违约现象;若净资产大于到期的债务,只要出售一定的股票就可以偿还债务,不会违约。对于上市公司股东来说,净资产收益状况和以该公司股票为标的的欧式看涨期权的损益状况是一样的,执行价格是到期的债务。所以,对于买方期权来说,如果股票的市值大于到期的债务,就属于价内期权,否则就不会执行该期权。

图1 看涨期权关系图
在图1的看涨期权关系中可以看出,如果公司净资产市值OA小于作为执行价格的负债额OB时,公司股东不会执行该期权,决定违约,最大损失为他所持有公司的股票市值P。只有当OA大于OB时,才会执行该期权,偿还到期的债务。
从上文的分析中可知,计算出公司的未来股票价格是很重要的。假如已知公司负债额和期限,资产的现值及资产市值的波动性,就可以运用Black-Scholes期权定价公式或者比较一般的期权定价公式求出公司的股票价格。KMV模型是在Black-Scholes的期权定价模型的基础上做了一定的创新。其中Black-Scholes模型可以表示为:
(1)
在模型中S 为股票价格,X为期权执行价格,V为企业资产价格,B为债务金额,r为无风险利率,σs和σv分别为企业股权价值和资产市值的波动率,τ为股票看跌期权到期日或贷款期限(或称违约期限)。上述两等式中,变量符号上方加短横线的表示该变量可以从市场上直接观测到。KMV模型的创新之处是站在借款企业股东的角度分析贷款问题,运用企业的股权市值与资产市值之间的关系和企业的股权市值波动率与资产市值波动率之间的关系模型,求出企业的资产市值V和资产市值变动率σv,进而再求出公司的EDF。
KMV模型推到EDF主要分为三个步骤。第一步,从公司股票的市场价值(S)、股价的波动性(σs)及负债的金额(B)估计出公司的市场价格(V)及其波动率(σv)。第二步,设计公司的违约点DPT以及计算违约距离DD。其中违约距离是指从公司的预期未来价值到违约点之间的距离是标准差的多少倍。第三步,估计EDF。这一步是要根据公司的违约的历史数据来确定。以下是具体的模型解释。
第一步,公司的市场价格V与其波动率σv的估计。
正如上文中所述,公司的市场价格(V)及其波动率(σv)是无法观测到的,需要通过模型来计算。KMV公司在期权定价公式中使用的是Vasicek-Kealhofer模型,而VK模型属于KMV公司的商业秘密没有公布。但是,我们通过选取合适的模型也能计算出V与σv。
根据Black-Scholes期权定价公式模型,可以得到以下表达式:
E=VN(d1)-De-rτN(d2)=f(V,σv,r,D,t)
(2)
其中:E为公司股权市场价值,D为公司负债的账面价值,V为公司资产市场价值,t为债务偿还期限,r为无风险借入或贷出利率,N(d) 为标准累积正态分布函数,它依据d1、d2计算而得。
其中d1、d2分别为:
(3)
(4)
公式(2)中有两个未知数——公司的市场价格(V)及其波动率(σv),对等式两边求导后再求期望可得到如下式子:
(5)
将已知的变量带入(2)、(5)式子中,联立两式,就可以求出公司的市场价格V及其波动率σv。
第二步,设计公司的违约点DPT以及计算违约距离DD。
正如我们上文所讲到的,当公司资产预期市场价值低于债务账面价值时,就会发生违约事件。其中,从理论上讲,到期的债务账面价值就是违约点DPT,只要公司预期的资产收益大于DPT,就不会发生违约。但是,在债务总额中的长期债务可以对公司的偿债压力起到缓解的作用。KMV公司通过对大量的历史数据进行了分析,发现公司的违约点DPT一般处在公司净资产市值大于等于流动负债加上50%的长期负债。这属于KMV公司的商业秘密,并没有对其做出解释。
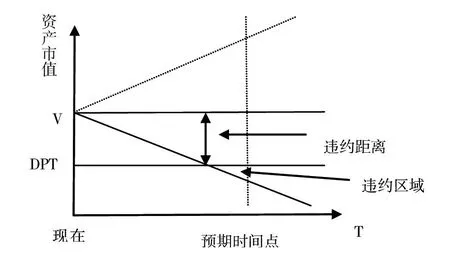
图2 理论违约距离与违约概率图解
有了违约点以后,就可以计算违约距离DD。违约距离就是指公司的资产市场价值到DPT的距离。当DD数值越来越大,公司的资产市场价值就离DPT越来越远,违约的可能性就越小;反之,违约的可能性就越大。当DD数值为负,公司将会违约。如图2所示。
从图2可以看出,公司在预期的时间点上,净资产市值低于DPT的部分为违约区域,资产预期期望值V到DPT的距离为违约距离,当预期的净资产市值低于DPT,就到了违约区域,公司就会违约。具体的计算模型如下:
(6)
式子中的E(V)为预期净资产市值,σv为资产波动率,DD是违约距离,DPT为违约点。
第三步,估计EDF。
有了第二步违约距离的计算,只要已知资产市值的概率分布就可以计算违约概率EDF。通常我们假定公司资产市值服从正态分布或者对数正态分布,公司的违约概率就是公司资产市值低于债务的概率(Merton,1974)。则,违约概率为:
EDF=Pt=P(Vt≤Dt|V0=V)=P(lnVt≤lnDt|V0=V)
(7)
式子中,Pt为公司的违约概率,V0是公司资产初始价值,Vt是公司资产当前价值,Dt为公司债务当前价值。
T时刻公司资产的市场价值为:
(8)
其中:μ为期望净资产回报率,σ为资产的波动率。
结合(7)、(8)可得公司的违约概率为:
(9)
在Black-Scholes模型中假定,公司资产预期收益率的随机变量服从标准正态分布,ε~N(0,1),公司的违约概率可以根据累积正态分布可知为:
(10)
由于违约距离为资产市值到违约点的距离,所以,可求出:
(11)
这样求出的EDF是理论上的EDF,EDF还有一种类型,就是经验的EDF。KMV公司选择的是后者。理论上的EDF认为违约距离为4个标准差公司的违约概率几乎为零,但从现实中看,这样的公司也会经常发生违约。由于KMV公司拥有大规模的历史违约数据,它可以将DD转化为每一个公司的经验违约概率,从而来评价公司的信用风险。这样,经验的EDF就成了DD的函数。同时,经过了对不同类别的公司的违约距离与违约概率之间的关系测算,KMV公司发现了稳定的函数关系。违约距离与违约概率之间的关系图如图3所示。

图3 违约距离(DD)与期望违约概率(EDF)关系图
从图3中也可以看出,EDF随着DD的增大而逐渐变小。
违约概率的计算公式如下:
(12)
从公式中可以看到,经验的EDF需要大规模的数据。由于我国关于地方政府信用违约相关的统计资料不完全,所以本文计算的是理论的EDF。
当然模型也存在着一些缺陷。从上文可以看出,预测违约概率主要是依靠上市公司的股票价格,这将对模型的精确性大打折扣。因为,在股票市场上,价格与价值的背离是经常发生的,所以这对公司的价值预测的准确性将会下降。并且,模型中在计算违约概率的过程中,假设了公司资产价值服从正态分布,这与现实不符,并不是所有公司的资产价值都服从正态分布。在债务结构上,KMV模型也没有充分的分析。KMV模型属于一种静态分析模型,并没有对公司的偿还顺序等考虑进来。
(二)KMV模型在地方债中的应用
类似于企业,地方政府也可以举债。影响地方政府债务发行规模的主要因素是地方政府的财政收支。相对于KMV模型在企业中的应用,KMV模型在地方债中的应用可以将企业的净资产价格替换为地方政府的财政收入。当地方政府债务到期时,若财政收入大于到期的债务额时,地方政府不会发生违约现象;若到期的债务额大于财政收入时,地方政府违约的可能性很大。如图4所示,违约距离为财政收入的均值到违约点的距离,违约距离越大,违约的可能性越大。图中的阴影部分是预期时间点的期望违约概率。
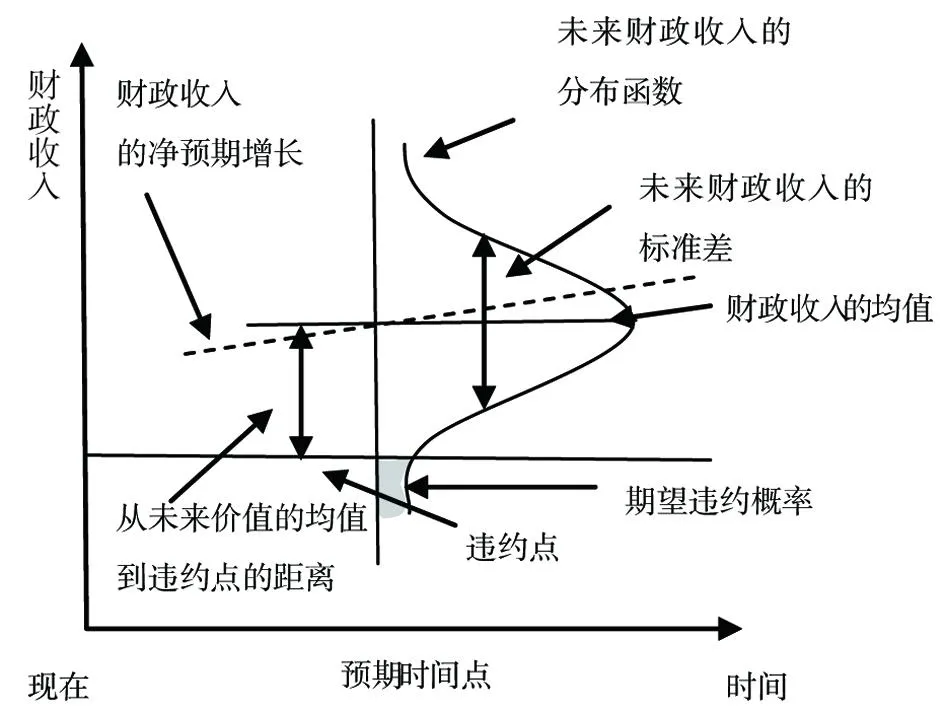
图4 地方政府债券信用风险模型
由于地方政府在偿还债务时,必须先保障地方政府能够正常的运转,所以和企业债务到期时的净资产市值相对应的是地方财政收入的担保。因此,模型需要确定一定比例的财政收入作为到期债券的担保。
综上所述,本文借鉴韩立岩(2003)的方法,构建以下地方政府债券信用风险度量的模型:
FRt=f(Zt)
(13)
其中,FRt为t时刻地方财政收入,Zt为随机变量,f(x)为特定函数。
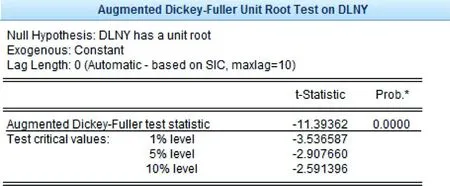
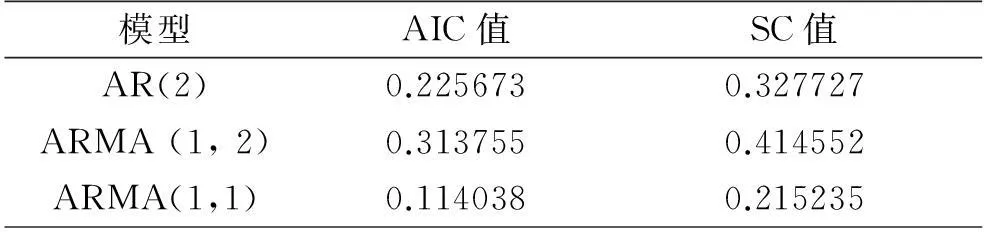
当地方债券到T期时,到期债券规模为BT,如果此时地方财政收入FRt小于到期债券规模BT,即FRt 本文假设地方财政收入服从几何布朗运动过程,即: (14) 其中,FRt为地方政府第t期的财政收入,dFRt为地方财政收入的变动量,dZt为标准几何布朗运动增量,μ为地方财政收入瞬时增长率,σ为地方财政收入的波动率。令t=0时,FR0=FR,则当t>0时,由14式地方财政收入可以表示为: (15) 其中Zt服从标准正态分布,则地方财政收入服从对数正态分布,由其性质可知相应的均值和方差分别为: (16) Var[lnFRt]=σ2t (17) 结合16、17式,可得: (18) (19) 由于地方财政收入的对数服从正态分布,所以地方债券违约距离与违约概率分别为: (20) P=N(-DD) (21) 其中N(·)为标准正态分布函数。模型表示当到期债务规模越接近于财政收入,债券的违约距离就越小,违约概率就越大。 五、实证分析 本文选择以内蒙古自治区为例,对自治区级地方政府债券的违约风险进行测度。伴随着经济发展进入新常态,内蒙古的财政收支状况不容乐观。近几年来看,内蒙古自治区财政总收入和本级政府性基金预算收入都未完成年度预算,本级政府性基金预算还有所减少。一是因为营改增的推进,导致地方政府税收收入进一步萎缩;二是因为近几年煤炭价格的下降,煤炭企业连年亏损,导致相关的税收减少和煤炭价格调节基金短收。再加上完善民生投入保障机制的刚性需求,导致内蒙古自治区财政缺口进一步扩大,这使得偿还到期债务资金的来源充满不确定性。由此可见,对内蒙古自治区政府债券的风险进行评估,以及测算安全的发债规模是很有必要的。 从地方政府的角度来说,在发行地方债券时应该首先考虑的是未来的偿债能力。面对内蒙古自治区弱财政和民生支出的刚性增长,准确预测财政收入就变得十分重要。本文采用1949-2014年内蒙古财政收入预测2015-2017年内蒙古财政收入Y。由于财政收入是时间序列数据,所以先对其取对数进行单位根检验,运行Eviews7.0软件,结果如下: 图5 内蒙古财政收入对数时间序列的ADF检验结果 从图5中可以看出,该序列t检验统计值明显高于1%、5%、10%三个显著水平下的临界值,这说明内蒙古财政收入对数时间序列是非平稳序列。本文继续在单位根检验中对该序列的一阶差分进行检验,Eviews7.0软件运行结果如图6所示。 从图6中很明显可以看出,一阶差分后的序列t检验值-11.39362,小于1%、5%、10%三个显著水平下的临界值,表明一阶差分序列不存在单位根,是平稳序列。即财政收入序列是一阶单整,ARIMA模型的d值为1。接着就是确定p和q值。 图6 内蒙古财政收入对数一阶差分时间序列的 ADF检验结果 根据图7,结合图形本文尝试AR(2)、ARMA (1, 2)和ARMA(1,1)中来选择最合适的模型。本文选用AIC、SC两准则作为模型选择的标准,三个模型中,两大准则越小的模型越理想。表1是三个模型的AIC、SC值。 图7 dln(Y)的自相关偏自相关图 表1 三个模型的AIC、SC值 从表1中,可以看出模型ARMA(1,1)的AIC、SC值是三个模型中最小的,所以,ARMA(1,1)是对数一阶差分序列的预测模型。通过Eviews7.0软件,回归的ARMA(1,1)模型如下: LnYt=0.129105+0.142551LnYt-1+0.857449LnYt-2+et+0.984773et-1 (22) 确定模型和参数后,就要对拟合模型的适应性进行检验,通过判断模型残差是否为白噪声序列来检验拟合模型的适应性。本文通过模型残差相关图Q统计量和P值来判断残差序列是否为白噪声序列。通过Eviews7.0软件运行结果如图8所示。 由图8可知,p值都大于0.05,因此该序列的残差序列为白噪声序列。则用该模型,可预测得2015-2017年内蒙古地方财政收入分别为2097.159亿元、2386.218亿元和2715.013亿元。 图8 残差自相关偏自相关图 并不是所有的财政收入都可以用来偿还到期债券的利息和本金,绝大部分的财政收入要用来保障政府的基本职能。在财政收入担保的比例上,不同的学者有不同的看法。韩立岩(2003)是将一个阶段的地方财政支出的均值作为近几年的自发财政支出,扣除自发财政支出后的财政收入作为到期债权的担保,其中,自发性财政支出是财政支出回归模型的常数项。李腊生(2013)和茹涛(2009)是将基本建设拨款、企业技术改造投资设为可用于担保的地方财政收入。本文在确定担保收入的时候,是将一般公共服务、公共安全、教育、文化、社会保障和就业、医疗卫生和城乡社区服务这些刚性支出从财政收入中扣除。由于财政返还性收入和一般转移支付也是对刚性支出的一种保证。所以在确定担保收入的时候,先用刚性支出扣除返还性收入和一般转移支付,然后再与财政收入作对比,作为在财政收入中的担保比例。本文结合2009年到2013年的上述几项数据,并对这几年的财政刚性支出与财政收入的比值取均值为68%,则2015-2017年内蒙古自治区担保收入为财政收入的32%,即671.091亿元、763.5898亿元和868.8041亿元。 把财政收入数据代入到公式(18)和(19)中,通过Mathcad软件,可得1949年到2015、2016和2017年的均值μ与标准差σ的值如表2所示。 表2 2015-2017年内蒙古自治区财政收入 正如上文所述,地方政府融资渠道比较复杂,所以,地方政府债务数据不容易统计。由于内蒙古政府2014年公布了《内蒙古自治区政府性债务审计结果》,所以可以得到截至2013年6月底内蒙古自治区政府债务的账面余额。从审计结果中,也可以清楚的了解债务余额在2015-2017年的清偿情况。但是,2013年7月到2014年年底之间内蒙古自治区的负债数据就无法得到。上文也提到,地方政府的未来融资渠道的重点是地方政府债券,所以,本文假设,内蒙古自治区在2013年7月到2014年年底期间只通过政府性债券融资。债券的到期债务的计算公式如下: (23) 其中,ri为第i期末到期债券债务的利率,MVi为第i期末到期债券债务,rt为t时刻到期债券债务的利率,MVt为t时刻到期债券债务。 由式(23)可知,在计算债券到期债务时,利率、债务额和期限结构是重要的变量。由于《内蒙古自治区政府性债务审计结果》已统计截至2013年6月底债务未来清偿情况,所以,现在只需对2013年7月到2014年底的债券债务进行统计。在这段时间内,中央代内蒙古自治区发行的地方政府债券额度具体如表3所示。 表3 2013、2014年中央代内蒙古自治区发行的地方政府债券 数据来源:中华人民共和国财政部网站. 从《内蒙古自治区政府性债务审计结果》可知,截至2013年6月底债务未来清偿情况如表4所示。 表4 2013 年6月底政府性债务余额 数据来源:《内蒙古自治区政府性债务审计结果》. 所以,2015-2017年内蒙古自治区到期债务如表5所示。 表5 2015-2017年内蒙古自治区到期债务规模 根据上文所计算的2015-2017年内蒙古自治区到期债务、财政收入增长率的均值μ与标准差σ值和担保收入的值代入到(20)和(21)中,通过Mathcad软件的计算,可以得到相应的违约距离和违约概率,如表6所示。 表6 内蒙古自治区2015-2017年债务的 关于合适违约概率的选择,本文参考标准普尔 BBB或者穆迪Baa3对债券的预期安全违约概率的规定,将我国发行的地方债券的违约概率也应保持在0.5%之内,即违约概率在0.5%以下时,可以保障债权人利益,防止地方政府出现信用违约风险。从表6中可以看到,2015-2017年的违约距离逐渐增大,违约概率逐渐减小。2015年和2016年的违约距离分别为0.964757和2.025929,违约概率都大于0.5%,表明存在违约风险。并且,2015年的违约概率达到16.73334,说明违约风险很大。2017年的违约距离为3.058832,违约概率为0.111101,小于0.5,说明债务风险比较小,不会出现违约现象。 由于新《预算法》中规定,地方政府以后主要的融资渠道为地方政府债券,所以,只要分析内蒙古自治区的发债规模,就可以度量违约风险。地方政府债券从2009年开始每年都在发行,且最近几年都连年递增(见表7),则每年都要偿还一定的到期债务。为了分析的方便,则将每年的偿还额定为每年的发债规模(韩立岩,2005)。把上文中预测的2015-2017年内蒙古地方财政收入以及μ、σ值代入到公式(20)、(21),通过Mathcad软件连续的试算,可以得到2015-2017年内蒙古自治区三年期、五年期和七年期债券不同发债规模下的违约距离和违约概率,从中找出2015-2017年内蒙古自治区不同期限债券的安全发债规模。 表7 内蒙古自治区2010-2014年真实发债规模 数据来源:中华人民共和国财政部网站. 表8 内蒙古自治区2015年不同发债规模下的违约距离和违约概率 表9 内蒙古自治区2016年不同发债规模下的违约距离和违约概率 从表8、表9和表10中可以看到,当内蒙古自治区2015-2017年三年期债券的发债规模分别为67.11、76.36、和86.88亿元时,违约概率为0,表明不存在违约风险;当发债规模分别为218.10、251.22和288.44时,占2015-2017年财政收入分别为10.40%、10.53%和10.62%,违约概率为0.5%,达到了安全规模;当发债规模继续增大时,违约距离逐渐减小,违约概率不断增大,违约风险也越来越大。同样的,当内蒙古自治区2015-2017年五年期债券的发债规模分别为187.91、216.10和249.35亿元时,占2015-2017年财政收入分别为8.96%、9.06%和9.18%,达到了安全发债规模。并且,当内蒙古自治区2015-2017年七年期债券的发债规模分别为175.83、203.11、234.58亿元时,占2015-2017年财政收入分别为8.38%、8.51%和8.64%,达到了安全发债规模。 表10 内蒙古自治区2017年不同发债规模下的违约距离和违约概率 六、结论 地方政府债券有着不可忽视的违约风险,从实证研究结果可以看到,发债规模越大,债务的违约风险也就越强,所以,在地方政府的发债规模上的控制,对防范违约风险会有很大的作用。从《内蒙古自治区政府性债务审计结果》中可以看出,内蒙古自治区在2013-2015年是政府债务余额重要款期,偿债压力比较大,2015年和2016年相对于2017年而言,到期还债的规模很大。本文通过KMV模型测度出,2015年和2016年的债务违约风险比较大,所以,对风险的防范将变得十分重要。 将违约概率控制在0.5%之内,内蒙古自治区就达到了安全的发债规模。由此可见,内蒙古自治区三年期债券发债规模控制在当年财政收入的10.40%之内,五年期债券控制在8.96%之内,七年期债券控制在为8.38%之内,不会产生信用风险。 [参考文献] [1]马德功,马敏捷.地方政府债务风险防控机制实证分析[J].西南民族大学学报,2015,(2). [2]李腊生,耿晓媛,郑杰.我国地方政府债务风险评价[J].统计研究,2013,(10). [3]张玲,张佳林.信用风险评估方法发展趋势[J].预测,2010,(4). [4]韩立岩,牟晖,王哲兵.市政债券的风险识别与控制策略[J].管理世界,2005,(3). [5]韩立岩,郑承利,罗雯,杨哲彬.中国市政债券信用风险与发债规模研究[J]. 金融研究,2003,(2). [6]洪源,刘兴琳.地方政府债务风险非线性仿真预警系统的构建[J].山西财经大学学报,2012,(3). [7]丛树海,李生祥.我国财政风险指数预警方法的研究[J].财贸经济,2004,(6). [8]马亭玉,刘泽龙.基于改进的KMV模型的地方政府债券信用风险的度量的研究[J]. 中国外资,2012,(10). [9]茹涛.地方公债发行过程中的信用风险度量与融资规模研究[D].上海:复旦大学,2009. [10]周青.地方政府投融资平台风险管理与度量研究[D].重庆:重庆大学,2011. [11]卢小曼.基于KMV模型的地方政府债券安全规模测度[D].天津:南开大学,2011. [12]李江波.Knight不确定性下的市政债券信用风险度量——以北京市为例[D].北京:首都经济贸易大学,2010. [13]李昊.我国地方政府债务风险预警模型研究[D].大连:大连理工大学,2010. [责任编辑:高平亮] A Study on Default Risk Measurement of Local Government Bonds Based on KMV Model JIA Zhi-lian,WANG Zhou-xiang (School of Finance and Tax,Inner Mongolia University of Finance and Economics,Hohhot 010070,China) Abstract:After the implementation of the Budget Law of the People's Republic of China (2014 Amendment), the local government debt obtained legal status. The risk control of the local government bonds is particularly important. In this paper, take Inner Mongolia as an example, using KMV model to measure the default risk of local government bonds issued from 2015 to 2017, and predict the safe issuing scale of local government bonds in Inner Mongolia. The results show that there's default risk Inner Mongolia's government debt in 2015 and 2016, and there's no risk of default in 2017. In addition, when the issuing scale of three -, five - and seven-year bonds be controled in the current fiscal income of 10.40%, 8.96% and 10.40%, it will not produce the default risk. Key words:local government bonds; debt scale; default risk(一)ARIMA模型预测财政收入



(二)担保收入的确定
(三)财政收入增长率的均值μ与标准差σ值的确定

(四)到期债务测算




(五)内蒙古自治区地方债风险的评估

(六)预测违约概率以及安全发债规模