基于决策树算法在高校招生决策系统的应用与研究
基于决策树算法在高校招生决策系统的应用与研究
刘思宏
(安徽电子信息职业技术学院 软件学院,安徽 蚌埠 233060)
摘要:随着高校生源质量的下降,提高高校考生的报到率是当务之急.分析影响报到率的条件,预测报到结果,能够为院校招生教学等工作提供有价值的参考依据.结合数据挖掘技术中决策树ID3算法建立决策树模型,并结合BMH模式匹配算法及朴素贝叶斯方法对ID3模型结论进行验证,对提高报到率具有一定的实用价值.
关键词:决策树;ID3算法;模式匹配算法;朴素贝叶斯方法
中图分类号:TP391文献标志码:A
文章编号:1008-5564(2015)03-0071-03
收稿日期:2015-04-01
作者简介:肖丹妮(1983—),女,陕西户县人,中国兵器装备集团摩托车检测技术研究所助理工程师,硕士,主要从事催化转化器贵金属检测研究.
ApplicationandStudyofEnrollmentDecisionSysteminCollegeBasedontheDecisionTreeAlgorithm
LIUSi-hong
(SchoolofSoftware,AnhuiVocationalCollegeofElectronics&InformationTechnology,Bengbu233060,China)
Abstract:With the decrease of college students’ quality, it is a task of top priority to improve the registration rate of college examinees. Analyzing influence factors of the registration rate and predicting the results of the registration could provide a valuable reference for enrollment and teaching work in colleges. The decision tree model was constructed based on the ID3 algorithm of decision tree of data mining technology, and the conclusions of ID3 model were verified based on BMH pattern matching algorithm and naive Bayesian method, all of above have important significance and practical application value in improving the registration rate.
Keywords:decisiontree;ID3algorithm;patternmatchingalgorithm;naiveBayesianmethod
随着现代高等教育的全面普及,在适龄生源数量逐年下降的现实情况下,即使高校自1999年开始扩大普高计划,但是依然呈现出报到率较低的现象.部分农村考生因地区、专业、家庭经济等原因放弃入学,同时选择打工和出国的考生也日趋增加.利用决策树技术,分析影响报到率的条件,预测报到结果,能够为院校招生、教学等工作提供有价值的参考依据.
1数据挖掘和决策树
数据挖掘(DataMining)从技术角度定义,是从大量的、不完全的、有噪声的、模糊的、随机的实际数据中提取隐含在其中的、人们事先不知道的、但又是潜在有用的信息和知识的过程[1].目前数据挖掘已经充分应用的方法包括:概念/类描述、关联分析、分类预测、聚类、孤立点分析、演变分析等[2].
决策树(Decisiontree),又称判定树,是数据挖掘中常用的建模方法以实现分类的功能.20世纪60年代Hunt首次提出这个概念,后由Quinlan等人根据信息论中的信息熵(Entropy)的思想提出决策树的经典ID3算法,其基本思想是根据信息熵以及信息增益的概念,将含有最高信息增益的属性作为当前结点的训练测试属性,建立二叉树决策模型[3].信息熵值的大小直接决定决策树建树分枝的判定条件.信息熵值越小,训练子集划分时的纯度越高.当所有数据记录均划分于相同类别时,或所有数据记录均具有相同属性时,则停止分类.
ID3算法描述如下:
算法:(ID3buide_dt)生成决策树
输入:训练样本集,所有属性归纳为属性集
输出:决策树
①创建一个节点N;
②如果所有训练样本集均属于相同的类C,那么
③返回节点N作为叶子节点,类C为标记;
④如果属性集A为空,那么
⑤返回节点N作为叶子节点,记为训练样本集中的类;
⑥选择属性集A中计算为最高信息增益的属性Sa;
⑦标记节点N为测试属性;
⑧划分训练样本集,对每个测试属性中的值a进行划分;
⑨建立测试属性值=a的子树s,s为训练样本集中测试属性=a的样本集;
⑩如果s为空,那么
2建立决策树系统原型
2008年至今,高校平均报到率一直维持在80%~85%左右,部分热门地区热门专业近年招生趋势稳定,但是不同地市考生的报到率却每况愈下,且申请调换专业的考生较多.为了能够真正的招到分数高、生源质量好且满足招生院校专业计划的生源,着实能够提高报到率,现利用决策树ID3算法建立招生决策系统模型原型.
2.1数据的收集与预处理
以安徽某高校近年招生录取数据作为训练样本集.该校招生的生源对象以安徽省内为主,现将数据训练样本集对省内地市作分析.在数据库中随机抽取录取信息500条记录,将录取数据库和实际报到数据库进行联接,得到“新生信息表”,定义条件属性字段包括:性别、户口类别、考生类别、归属地区、专业类别、成绩类型、录取批次.将成绩做概化处理400分以上(含400分)概化为“好”;300~399概化为“较好”;200~299概化为“一般”.
2.2建模分析
分别对考生成绩(好、较好、一般)、考生类别(应届生、历届生)、考生科类(文科、理科)、考生户口(城镇、农村)、生源地(本市、皖北、皖南)等多个条件进行分类.
2.3建立决策模型原型
利用ID3算法及其改进方法将决策树的根节点和分支属性节点分别计算.
建立根节点:已知训练样本集E是n维有穷向量空间,包含了i个不同的属性类,将E划分为i个类的信息熵,有:
Entropy(E)=∑-p(i)log2p(i)
(1)
在录取数据库中随机抽取的500条数据中,得到452条考生记录已报到,利用式(1)计算熵可得:Entropy(A,学生报到)=-(452/500)log2(452/500)-(48/500)log2(48/500)= 0.456 1.
计算条件属性熵:若选择属性A的每一分支节点上,选择A导致的期望熵值定义为每个子集E的加权和,有
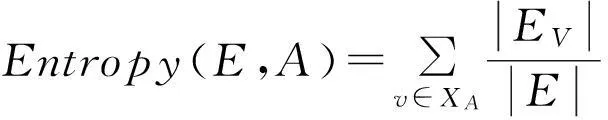
(2)
以专业节点属性为例,计算“专业”条件属性熵,利用式(1)计算属性值熵:
Entropy(A制造)=-(58 /70)log2(58 /70)-(12 /70)log2(12 /70)=0.660 9
Entropy(A电子信息)=-(236/272)log2(236/272)-(36/272)log2(36/272)=0.563 8
Entropy(A材料与能源)=-(43/50)log2(43/50)-(7/50)log2(7/50)=0.584 2
Entropy(A财经)=-(40/48)log2(40/48)-(8/48)log2(8/48)=0.650 0
Entropy(A文化教育)=-(57/60)log2(57/60)-(3/60)log2(3/60)=0.286 3
将上述计算数值代入式(2)计算属性熵:
Entropy(A,专业)=(专业子集数/500)*Entropy(A|专业名称=…)=(70/500)*0.660 9+(272/500)*0.563 8+(50/500)*0.584 2+(48/500)*0.65+(60/500)*0.286 3=0.554 4
计算条件属性增益:属性A相对训练样本集E的信息增益Gain(E,A)定义为:
Gain(E,A)=Entropy(E)-Entropy(E,A)
(3)
利用式(3)计算条件属性增益:Gain(A,专业)= 0.562 8-0.554 4=0.008 4
依次按照上述公式进行决策属性计算,最终得到决策树模型原型如图1所示:
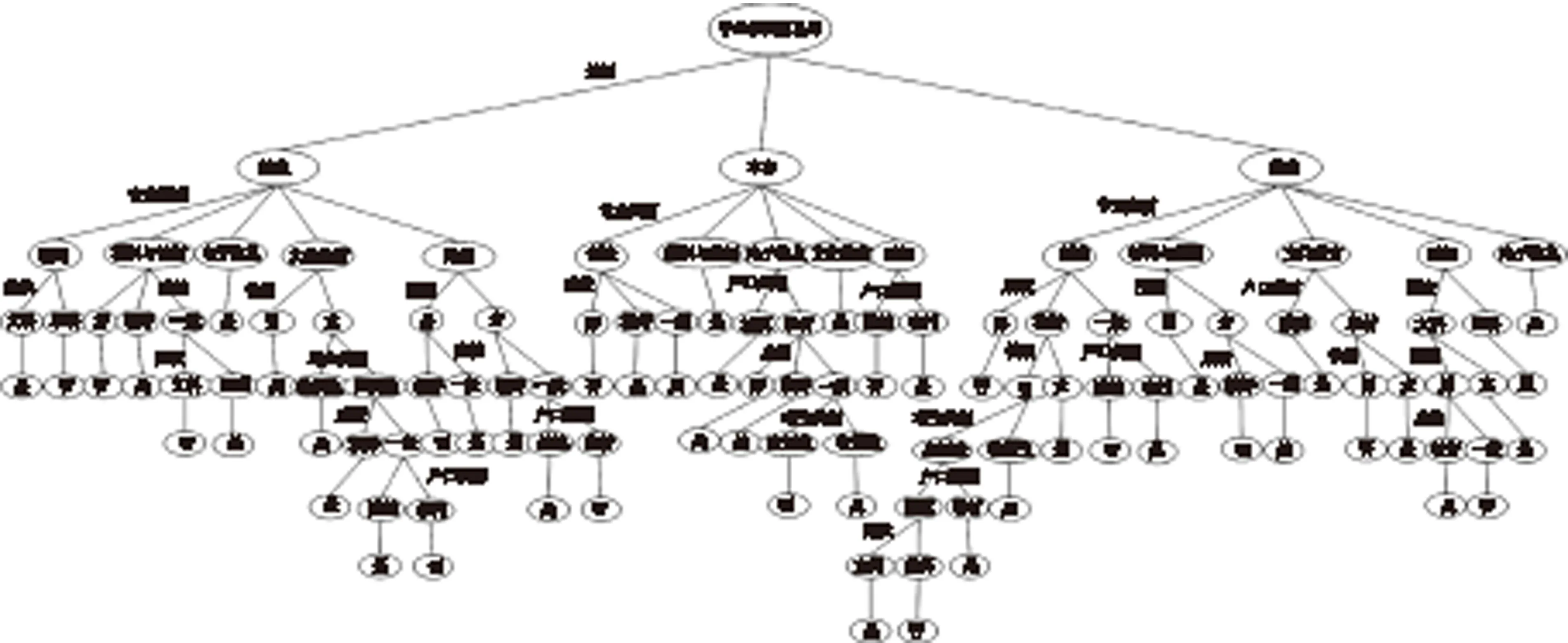
图1 决策树模型原型
2.4得出分类规则
根据决策树模型原型得到分类规则,采用IF…THEN的形式将各个分类条件下,考生是否报到的结果直观显示出来,如图2所示.

图2 分类规则结论
3建立决策验证系统
3.1模式匹配算法
模式匹配算法是指将两个模式作为输入,计算模式元素之间语义上的对应关系的过程.字符串模式匹配算法是在给定的字符集中,判断一个模式串(字符串)是否在给定的文本串(文本)中出现[4].在上述招生录取数据库中可以认定整个录取数据库作为一个完整的长字符串,通过行的顺序逐一连续起来,利用模式匹配算法中的匹配次数作为统计数量的结果,将统计数字的所占的比例作为下次匹配计算的值.所得到的计算结果可以让决策者更加直观的看到各个条件下学生的报到率,如图3所示.
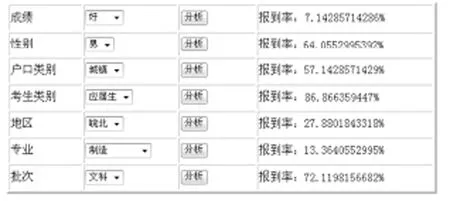
图3 模式匹配算法分条件报到率统计
3.2朴素贝叶斯分类方法
朴素贝叶斯分类(NaiveBayesClassifier,简称NBC)在贝叶斯统计的基础上建立了分类模型,利用概率计算的思想,在统计学等诸多领域实现预测的功能.
贝叶斯定理[5]设S是类标号未知的数据样本,设H为某假设,若数据样本S属于某特定类C.在分类问题中,我们希望确定P(H|S),即给定测试样本X假设H成立的概率.在此验证系统中,利用模式匹配算法作为分条件匹配统计结论,结合朴素贝叶斯方法将上述分类规则进行验证.

图4 朴素贝叶斯方法验证结果
验证分类规则:取条件={IF地区=“皖南”AND专业=“文化教育”AND户口类别=“农村”AND性别=“女”}
验证结论={是否报到=“是”}
验证结果如图4所示.
3.3验证结果分析
从上述模式匹配算法和朴素贝叶斯方法相结合的计算中,我们得出以下结论:
①当前测试训练样本集中,利用决策树方法ID3建立模型得到分类规则的条件与结论与朴素贝叶斯方法验证较一致.在验证过程中,根据判定条件得出的决策属性个数,统计分条件下的考生报到率.根据已知条件预测出较为准确的结论是能够帮助决策者做出决策的重要方法.
②模式匹配算法较为有效、准确地统计出分条件报到人数,对分专业报到率,分地区报到率,分批次报到率等做出详尽统计,统计结果能够得出直观的结论.同时,统计值可作为朴素贝叶斯的先验概率,避免了手工计算的繁杂.
4结语
本文研究数据挖掘中的决策树技术,针对决策树技术和朴素贝叶斯的分类方法进行讨论,结合实际高校的招生录取报到数据,提出利用ID3算法生成决策树模型原型,根据分类规则产生的结果分析影响高校考生报到的关键条件,并将模式匹配算法和朴素贝叶斯方法相结合进行验证,辅助决策者对于招生宣传、专业制定、课程设置等相关工作的预测,能够更有利于应对市场变化,提高报到率,为高校决策提供一定的辅助作用.
[参考文献]
[1]HANJia-wei,KANBERM.Dataminingconceptsandtechniques[M].MorganKaufinannPress,2001:186-201.
[2]成平广.ID3算法在高校招生决策中的应用研究[J].重庆教育学院学报,2008,21(3):44-46.
[3]黄文.决策树的经典算法:ID3与C4.5[J].四川文理学院学报(自然科学版),2007,17(5):16-18.
[4]刘胜飞,张云泉.一种改进的BMH模式匹配算法[J].计算机科学,2008,35(11):164-173.
[5]叶丹,刘坤.基于朴素贝叶斯分类的高校招生宣传决策系统[J].井冈山学院学报(自然科学版),2008,29(8):27-29.
[责任编辑王新奇]
Vol.18No.3Jul.2015

