规整填料生产中冲制折边垂距及其误差研究
规整填料生产中冲制折边垂距及其误差研究
叶素娣1,2,徐敬华2
(1.芜湖职业技术学院 电气工程学院,安徽 芜湖 241006; 2.浙江大学 机械工程学系,杭州 310027)
摘要:对空分设备中金属孔板波纹规整填料片几何结构进行分析,构建填料片冲制侧面与理想平面间的折边垂距参数模型,通过四面体体积变换法与Taylor级数展开法,得出折边垂距及其误差计算公式,并得到冲制折边几何偏差随着填料直径增大呈幂级增长的结论.改进填料片的生产工艺,减小整个填料长度上折边垂距的误差波动,从而改进气液分离中压降与操作气速的关系.
关键词:规整填料;冲制折边;垂距误差;压降;操作气速
中图分类号:TQ9文献标志码:A
文章编号:1008-5564(2015)03-0063-04
收稿日期:2015-03-15
基金项目:安徽省2014年高等学校质量工程项目:产教融合、校企合作数控技术专业人才培养模式创新与实践(2014jyxm598)的阶段性研究成果
作者简介:毕亚东(1981—),男,陕西宝鸡人,安徽国防科技职业学院机械工程系讲师,硕士,主要从事机械设计及其理论研究.
StudyontheCoiningRuffledOffsetanditsErrorduringtheProductionofStructuredPacking
YESu-di1, 2,XUJing-hua2
(1.SchoolofElectricalEngineering,WuhuInstituteofTechnology,Wuhu241006,China;
2.DepartmentofMechanicalEngineering,ZhejiangUniversity,Hangzhou310027,China)
Abstract:The piece geometry of structured packing of corrugated metal plate with hole was analyzed, and the parameter model for the ruffled offset between the coining side of packing sheet and the ideal plane was built. The coining ruffled offset and its error calculation formula were derived by using of the method of tetrahedral volume transformation and Taylor series expansion, and in conclusion that the geometrical deviation of the coining ruffled was increasing exponentially with the increase of packing diameter. By means of improving the production technology of the packing piece and reducing the error fluctuation of the coining ruffled offset along the whole packing length, thus the relationship between drop of pressure and operating gas velocity in gas-liquid separation was improved.
Keywords:structuredpacking;coiningruffled;offseterror;dropofpressure;operatinggasvelocity
金属孔板波纹规整填料是一种在空分塔内按均匀几何图形排布、整齐堆砌的填料,它规定了气液流路,改善了沟流和壁流现象,具有大通量、低压降、高传质表面,分离效率高,放大效应小,抗污染能力强等优点,在空分精馏塔中有广泛的应用.
规整填料组装时相邻两波纹片反向靠叠,使填料片间形成交叉三角形通道,各片高度相同但长度不等,搭配组成圆盘状装于塔内.文献[1-3]分析了规整填料的性能与其几何尺寸、倾角、波纹齿角的关系,文献[4-6]通过CFD或实验方法研究填料的流体力学性能和传质性能,文献[7-9]对规整填料的现状及发展趋势进行了详细的分析,但文献[1]在分析波纹形规整填料的几何关系时,忽略冲制工艺中冲制侧面与理想平面间存在的折边垂距,假想冲制侧面就是理想平面,而实际工程中折边垂距是一定存在的,并且折边垂距还有复杂的误差,这两项因素对气液分离性能将会产生的影响,还鲜有研究.
本文通过对规整填料片几何形状的研究,提出折边垂距的概念,推导出折边垂距及其误差的计算公式,分析了填料片实际成型过程的折弯圆角半径对比表面积和波纹顶角的影响,设计填料生产工艺的改进措施,减小折边垂距误差从而提高气液分离性能.
1规整填料折边垂距和折弯半径的分析
图1~3为规整波纹填料片及其法截面图,图1是倾角45°的两相邻填料片,A-A剖面显示填料片法截面形状,基本参数有波距2B、波高H和波纹顶角ξ,片厚t以及半峰波长S.
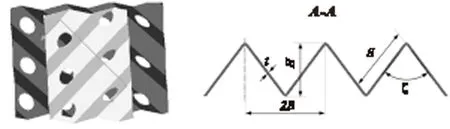
图1 倾角为45°的相邻填料片及法截面
1.1用四面体体积变换法推导规整填料的折边垂距

图2 填料片的三维坐标
建立图2所示的三维坐标系,取填料片上相连的三个波纹斜齿L1、L2、L3置于坐标系XYZ中.设φ为波纹倾角,过AC作XY平面的垂直面AB′C与过点B的垂线交于B′,则BB′称为折边垂距,设为h.过A点作AA1的垂面ADE分别交BB1、CC1于D、E,则∠ADE为波纹顶角ξ;设M为AC的中点,MB和MB′所夹角设为折边夹角θ,则h=Htgθ;取A1C1的中点R1,作PR1垂直于A1C1交AA1于P点,在斜面ABB1A1上过点P作A1B1的垂线PQ交A1B1于Q点,在A1B1C1面上过Q点作QR垂直于A1B1交A1C1于R点,连接PR.
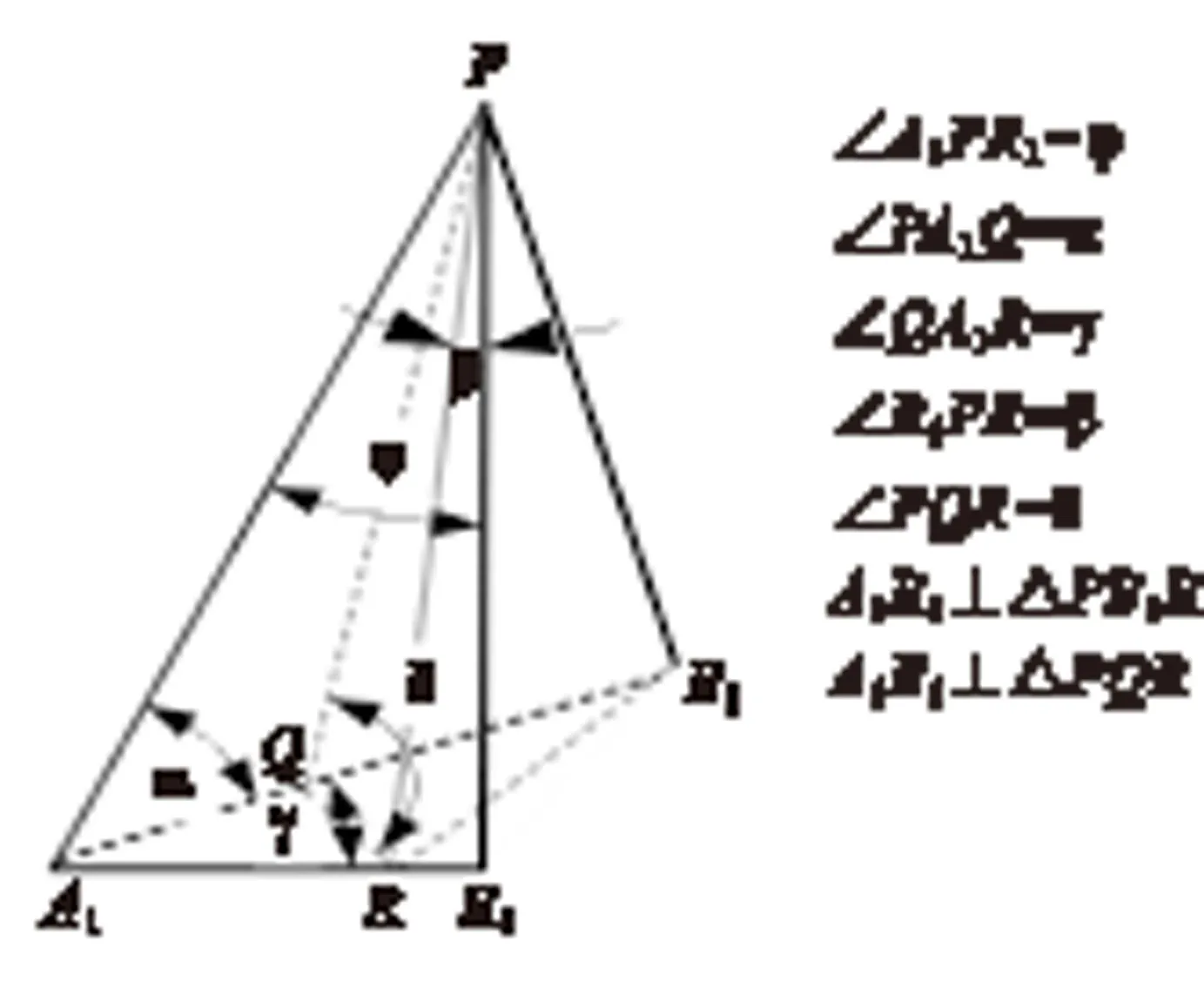
图3 填料局部放大图
图3为图2的局部放大图,在Rt△A1PQ,Rt△A1RQ,Rt△A1PR1中分别有下列公式成立:
得到:
cosα/cosγ=sinφ-cosφ·tgβ
(1)
在Rt△AND,Rt△ACE,Rt△ABM,Rt△BMB′中,分别有下列等式成立:
tg(ξ/2)=AE/2·H,cosφ=AE/AC,
ctgγ=AM/BM,cosθ=H/BM
得到:
cosθ=cosφ·ctgγ·ctg(ξ/2)
(2)
在Rt△ABD,Rt△ACE,Rt△ADN中,分别有下列等式成立:ctgα=BD/AD,tgφ=CE/AE,sin(ξ/2)=AE/2AD
得到:
ctgα=tanφ·sin(ξ/2)
(3)
四面体P-A1B1R1体积的两种表达方式:
A1B1×S△PQR+RR1×S△PB1R1=A1R1×S△PB1R1
得到:
sinδ=cosθcosφ /sinγ
(4)
在△PQR中,由余弦定理知:
cosδ=(PQ2+QR2-PR2)/2PQ×QR
其中:PQ=PA1×sinα,RQ=A1R×sinγ,PR=PR1/cosβ
又
PA1/PR1=1/cosφ,A1R/PR1=tgφ-tgβ
得到:
(5)
与(1)联立消去β并化简得:
(6)
(6)与(4)联立消去δ,代入(2)(3),并设:
(7)
得到:
A·tg4θ+D·tg2θ+C=0
求解得到:
(8)
(9)
1.2规整填料片冲制折边过程中存在的折弯圆角半径
金属波纹规整填料片常用铝合金薄片,在冲制折边过程中,圆角过渡区内层纤维受压而缩短,外层纤维受拉而伸长.基于中性层长度不变原理,将直线部分和弯曲部分中性层长度直接求和得到规整填料半峰波长S,图4为考虑折弯圆角半径时的半个波纹截面图,设填料片折弯圆角半径为r,则有:
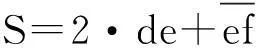
式中,de为弧长,2·de=(r+t/2)·(π-ξ)
即:
(10)
波纹顶角计算公式为:
(11)
比表面积计算公式为:
(12)
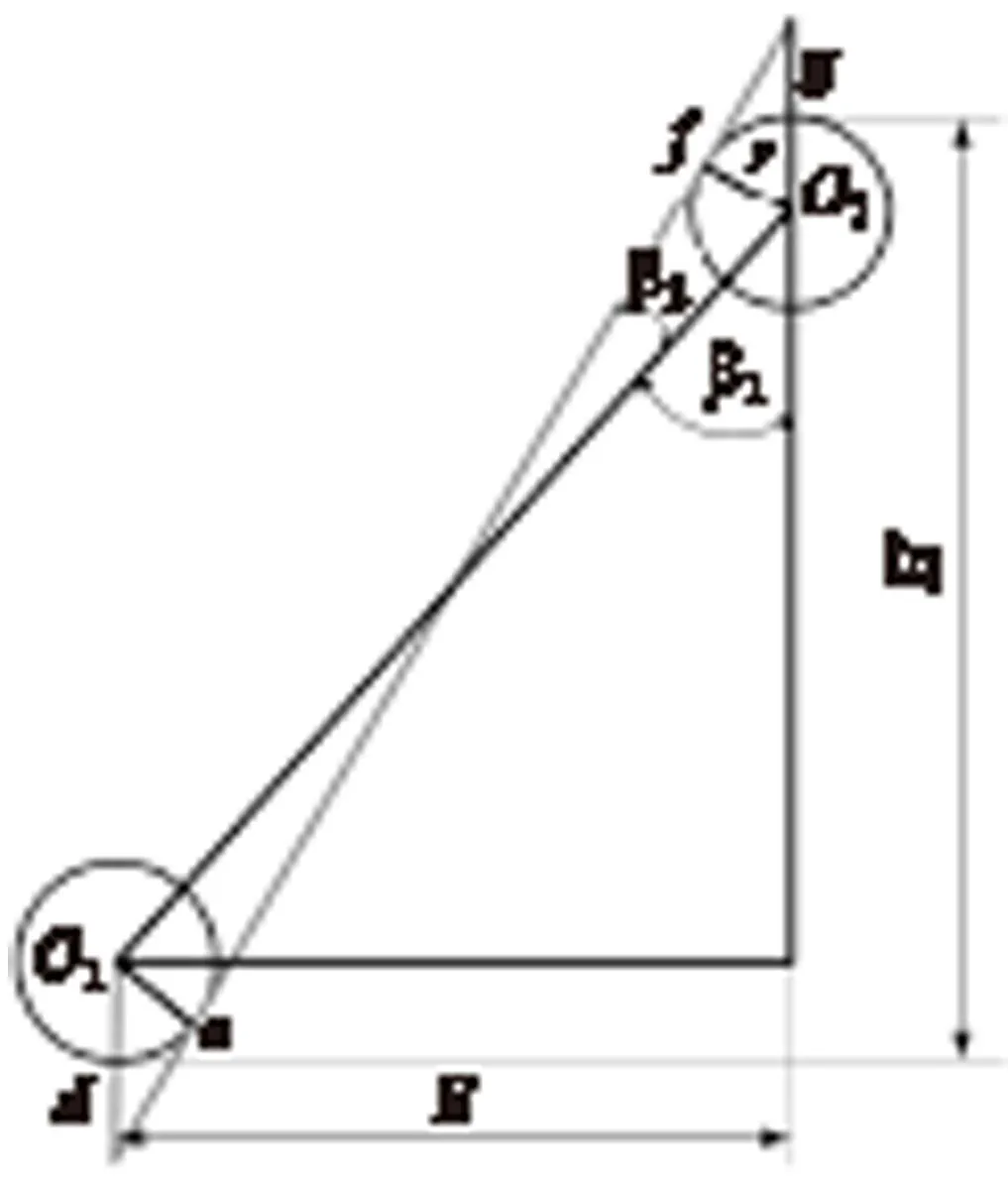
图4 考虑折弯半径r时的半个波纹截面

图5 折弯半径r与波纹顶角ξ和比表面积a
由图5可知,B、H和t一定时,ξ随r的增大而减小;a随r的增大而增大.波纹顶角ξ与填料压降有重要影响,减小波纹顶角,可减小压降,提高填料塔的通量和传质效率[3].
2规整填料折边垂距的误差分析及减小误差波动的工艺改进措施
2.1基于Taylor级数展开的规整填料折边垂距误差分析
由公式(7)(8)(9)可知,某一斜齿Li上的折边垂距h为H和θ的函数,而θ为φ和ξ的函数,ξ为B,H,r和t的函数,即:h=f(xi),其中xi为填料的参数B,H,r,t和φ.按Taylor展开并取一次项,得到折边垂距h的误差公式:
偏导为误差传递系数,某项参数的误差传递系数越大,说明该项参数对dh的贡献越大,设计时应适当减小该项参数的误差;或者,在某项参数误差不变的前提下,尽量使该项参数的误差传递系数最小化.
将式(9)求导得到下式:
dh=tgθ·dH+H·(1+tg2θ)·dθ
(13)

图6 填料长度方向各波纹斜齿基准误差
式中H,dH为已知量,tgθ可通过式(8)求得,而dθ可通过对式(8)求导获得.
在图2所示的整个填料片长度上,波纹斜齿L1、L2、L3…Ln依次相连,各波纹斜齿在XY上的基准面投影到XZ面上时成为互成夹角的线12、23、34…,图6所示.
假设各投影线12、23、34…等长且为k,夹角同向且为最大角η(用弧度表示):
Δxmax=k(1-cosη+1-cos2η+…+1-cos(n-1)η)
Δzmax=k(sinη+sin2η+…+sin(n-1)η)
用三角函数的Taylor级数展开,得到:
Δxmax= kη2(1+4+9+…+(n-1)2)/2=
kη2n(n-1)(2n-1)/12
(22)
Δzmax= k(1+2+…+n-1)η=
kηn(n-1)/2
(23)
Δxmax与n的三次幂成正比,Δzmax与n的二次幂成正比,即Δxmax∝n3,Δzmax∝n2,故最大基准误差随塔径的增大而急剧增大.
2.2采取工艺改进措施减小误差波动
由2.1的分析可知,折边垂距误差包含两个内容:dh和基准误差Δx、Δz.由式(22)(23)可知,当夹角η为零时,Δx=0、Δz=0.使图6中的12、23、34…等投影线在一条直线上,保证夹角η为零或接近零;公式(13)表明各参数的变化量dB、dH、dr、dξ、dφ影响着dh的大小,因此在生产填料片时要采取有效措施减小参数变动量,从而减小dh.
3实例分析
某塔器采用如图1所示的孔板波纹规整填料,设2B=7.1±0.5mm,H=4.2±0.5mm,r=0.5±0.2mm,t=0.2±0.02mm,φ=45°±2°,盘高L=25.4mm,由式(8)(9)可计算出折边夹角θ=9.04°,折边垂距h=0.67mm,由式(11)计算出波纹顶角的公称尺寸ξ=69.7°,由误差公式(21)和(13)求得dξ=±4.8°,dh=±0.17mm.
针对具体的金属波纹规整填料片生产,确定工艺改进措施:Step1,根据折弯公式F=650×K×t2×L/2B,其中K为材料的折弯压力系数,计算得到折弯单个波纹斜齿F=0.13kN,若所选折弯机压力为10T,则可连排上百个波纹斜齿,根据填料实际长度确定连排数;Step2,设计凹模V形槽宽度为7.1mm,并确定凸、凹模具圆角半径r=0.5mm,考虑到折弯回弹,凸、凹模具中波纹顶角设计为68°;Step3,按照图4中defg路线线切割加工连排凸、凹模具,保证各基准线夹角η为零或接近零.
在孔径、开孔密度相同的条件下,取工艺改进前、后的填料片进行对比性仿真实验.试验取相同参数:空气密度ρV=1.205kg/m3,空气压强为p=101.325kPa,空气粘度为μV=1.81×10-5Pa·s,水的密度为ρL=998.2kg/m3,水的动力粘度为μL=1.005×10-3Pa·s,表面张力σ=0.072 8N/m,水的流量为L=0.5m3/h,喷淋密度为15.2m3.m-2.h-1.
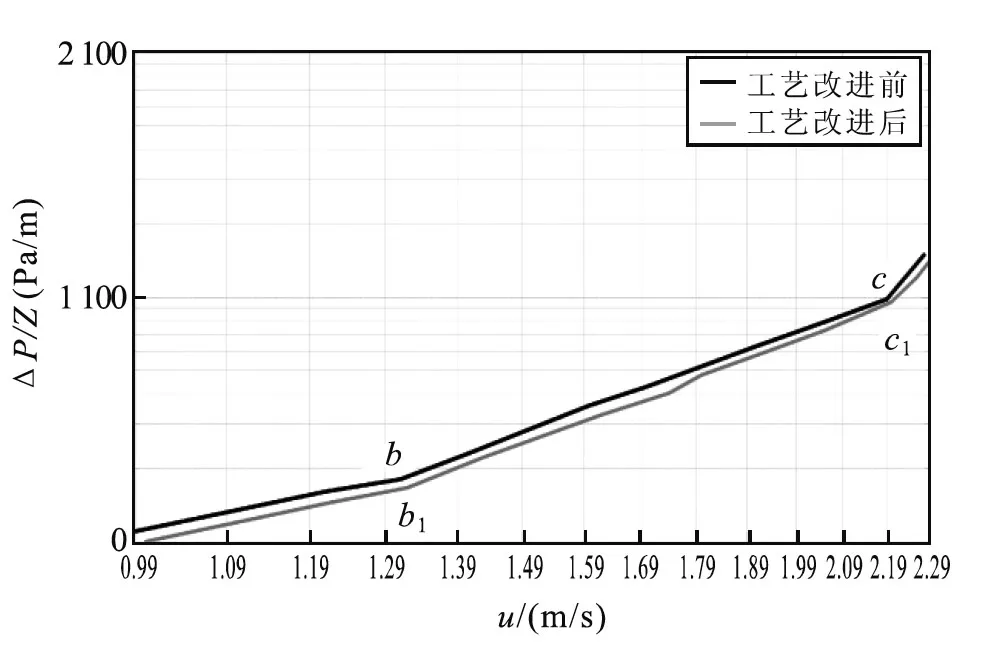
图7 操作压降与气速
以单位高度压降ΔP/Z和操作气速u为纵横坐标建立双对数坐标系,如图7所示.工艺改进后的曲线在相同的操作气速下有较小的压降;而在相同的压降下有较大的操作气速.将仿真试验结论通过物理实验进行了验证.
工艺改进前基准误差相当于增加了气体运行中的形体阻力,而工艺改进后基准误差降到最小,气体流通通道总体上呈现规则的“Z”形,因而在气体运行过程中压降减小,操作气速增大[5].
4结语
(1)针对填料的几何形状特点,提出折边垂距的概念,并根据几何关系推导出折边垂距及其误差计算公式.
(2)通过规整填料冲制折边工艺的改进,减小折边垂距的误差波动,通过仿真实验证明工艺改进措施的有效性.
[参考文献]
[1]袁孝竞,蓝仁水.波纹形规整填料的几何关系[J].化学工程,2004,32(6):20-23.
[2]朱慧铭,孙津生,吴锦元,等.空分上塔规整填料结构优化—波纹规整填料倾角的确定[J].化学工程,2001,29(1):11-15.
[3]罗淑娟,宋新月,费维扬.规整填料干塔压降与波纹齿角的关系[J].化工学报,2007,58(11):2764-2769.
[4]李群生,张德志,章慧芳,等.HX型高效规整填料的流体力学和传质性能研究[J].北京化工大学学报:自然科学版,2013,40(2):14-19.
[5]杨运财,陈桂珍,杨银如,等.规整填料传质性能计算的研究进展[J].化学工业与工程技术,2010,31(2):28-32.
[6]曾菁,李鑫.开孔与层数对丝网波纹填料流体力学性能的影响[J].化学工业与工程,2013,30(2):64-69.
[7]周伟,梁泰安,杜剑婷.提高塔填料效率研究[J].化学工程,2000,28(6):11-15.
[8]蒋庆哲,宋昭峥,彭洪湃,等.塔填料的最新研究现状和发展趋势[J].现代化工,2008,28(增1):59-63.
[9]李群生,马文涛,张泽廷.塔填料的研究现状及发展趋势[J].化工进展,2005,24(6):619-625.
[责任编辑王新奇]
Vol.18No.3Jul.2015

