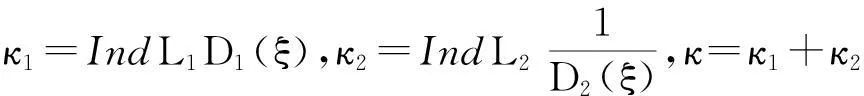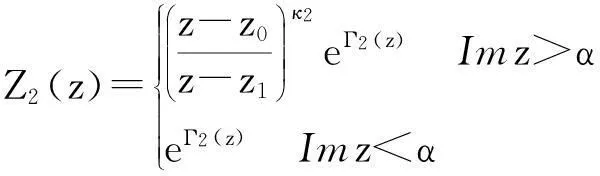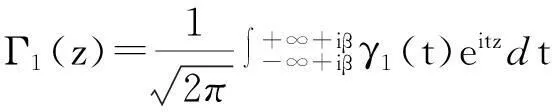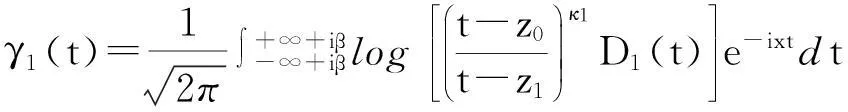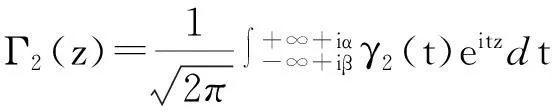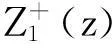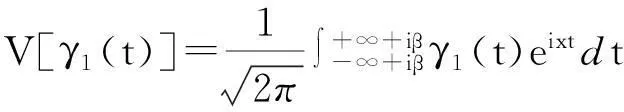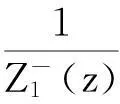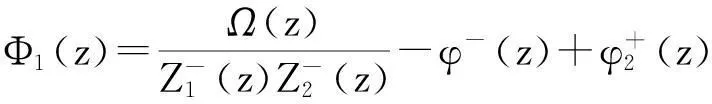双环形曲线的Riemann边值问题的求解

双环形曲线的Riemann边值问题的求解

张玉1，沈永祥2

(1.吉林师范大学 数学学院，吉林 长春 130013；2.吉林师范大学 数学学院，吉林 四平 132000)

摘要:利用封闭曲线Riemann边值问题的相关理论，讨论该问题的双环形曲线的Riemann边值问题之后转化为平行直线Riemann边值问题.讨论函数是否为典则函数，最后根据Lowville定理理解表达式.

关键词:Riemann边值问题；封闭曲线；正则型；Lowville定理

DOI:10.13877/j.cnki.cn22-1284.2015.10.012

收稿日期：2015-04-10

基金项目：国家自然科学基金“多元复分析中逆紧全纯映照问题研究”(11301215)

作者简介：张玉,女,吉林农安人,吉林师范大学数学学院在读硕士研究生.

通讯作者：沈永祥,吉林四平人，教授.

中图分类号：O175.6文献标志码：A

解析函数的基本问题称为Riemann边值问题，已有较多研究，应用背景也很丰富.通常的问题都是封闭曲线即单环曲线的Riemann边值问题.本文是在单环的基础上提出了双环形曲线的Riemann边值问题.在函数类{{0}}中给出了一般条件和可解条件，从而使经典的Riemann边值问题得到了推广.

1双环形曲线的Riemann边值问题的提法

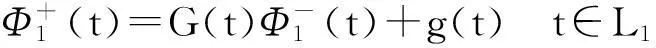
其中,G(t)、g(t)∈H(t)均为已知函数.

2双环形曲线的Riemann边值问题转化为平行直线的Riemann边值问题

设L1:Imz=β,L2:Imz=α(α<β),要求未知函数F(x)分别在Imz>β与Imz<α内解析，Ω(z)在α

(1)

其中,函数Dj(ξ),gj(ξ)分别在L1,L2上属于{{0}}.将(1)式改写为：

(2)

其中，

(3)

(4)

从而有

(5)

即

(6)

综上式(5)、式(6)，可得到当κ>α时，

参考文献：

[1]路见可.解析函数边值问题[M].上海:上海科学技术出版社,1987.

[2]沈永祥.关于Cauchy核和卷积核混合的奇异积分方程求解方法的研究问题[J].吉林师范大学学报,2003(1):49-51.

[3]Shen Yong xiang.A Kind of Integral Equation with both Two Convolution Kernels and Dual Type Property[J].Ann of Math.,1991,12(1):57-65.

[4]Shen Yong xiang.Some Kinds of Singular integral Equations of Hilbert Kernel with Convolution[J].Acta Math Sci.,1989,9(4):421-426.

[5]Shen Yong xiang.Two Kinds of Singular integral Equations with Convolution Kernel in the Non-normal Type Case[J].Northestern Mathematical Journal,1989,5(1):84-92.

(责任编辑:陈衍峰)