三维Hom-Novikov代数的分类

三维Hom-Novikov代数的分类

康健

(辽宁师范大学 数学学院，辽宁 大连 116029)

摘要:主要讨论复数域上的三维Hom-Novikov代数的分类，分别给出了Hom-Novikov代数与Hom-preLie代数的定义，利用定义及其性质，得出三维Hom-Novikov代数在特定的α对应矩阵形式下的分类情况．

关键词:Hom-Novikov代数；Hom-preLie代数；Hom-型代数

DOI:10.13877/j.cnki.cn22-1284.2015.10.006

收稿日期：2015-04-16

作者简介：康健,女,辽宁鞍山人,在读硕士.

中图分类号：O152.5文献标志码：A

Hom-Novikov代数与Hom-preLie代数分别是从Novikov代数以及pre-Lie代数通过代数变形而得到的一类Hom-型代数．Hom-Novikov代数与Hom-preLie代数有着密切联系[1-2]．近些年来，关于Hom-Novikov代数的研究已经有了一定的进展，例如,Yau给出了利用Hom-Lie代数及一个适当的线性同构构造Hom-Novikov代数的方法[3-4]．同时,Yau还给出了利用Novikov代数上的代数同态构造Hom-Novikov代数的方法[4]．对Hom-Novikov代数与Hom-preLie代数的研究，在某种意义上是对Novikov代数以及pre-Lie代数的深化，是对其概念与方法的延续，具有一定的指导和应用意义．

1基本概念

定义1[4]设A是数域F上的向量空间,μ:A⊗A→A是A上的代数运算,α：A→A是A上的线性变换并且满足：

α(xy)=α(x)α(y)

(1)

(xy)α(z)-α(x)(yz)=(yx)α(z)-α(y)(xz)

(2)

(xy)α(z)=(xz)α(y)

(3)

则称(A,μ,α)为Hom-Novikov代数．若A的代数运算μ以及线性映射α只满足(1)和(2)，则称(A,·,α)为Hom-preLie代数．

2三维Hom-Novikov代数的分类(dimAA=1)

设(A,μ,α)是三维Hom-Novikov代数，在同构的意义下，α不可逆时对应的三阶矩阵有以下几种情况：

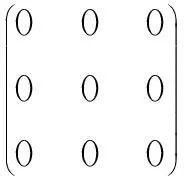
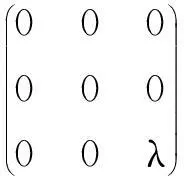
其中，λ≠0，λ1≠λ2≠0．

定理1三维Hom-Novikov代数的分类(dimAA=1)(表1)．

表1　三维Hom-Novikov代数的分类( dimAA=1)

可得

e1e1=a11e,e1e2=a12e,e1e3=a13e,

e2e1=a21e,e2e2=a22e,e2e3=a23e,

e3e1=a31e,e3e2=a32e,e3e3=a33e.

(4)

α(e1)=0,α(e2)=e1,α(e3)=e2

(5)

在(1)～(3)中x,y和z可取e1,e2和e3，利用(1)～(5)可以得到以下几种情况.

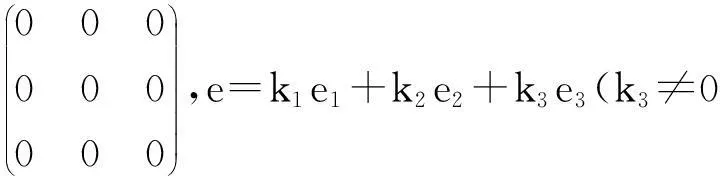
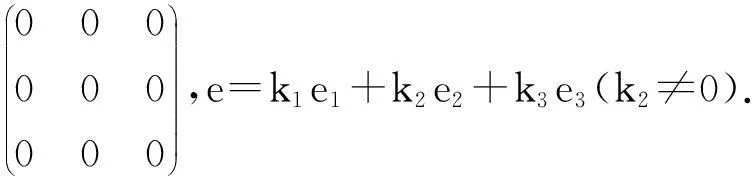
3三维Hom-Novikov代数的分类(dimAA=2)

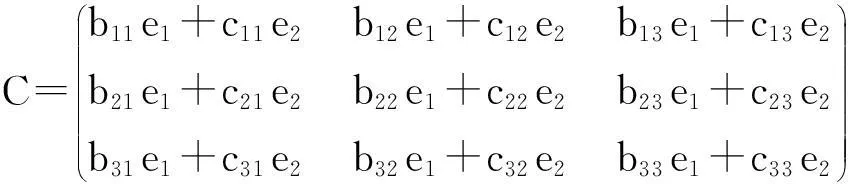
设(A,μ,α)是三维Hom-Novikov代数，在同构意义下，α不可逆对应的三阶矩阵有5种情况.

其中，λ≠0，λ1≠λ2≠0．

定理2三维Hom-Novikov代数的分类(dimAA=2)(表2).

表2　三维Hom-Novikov代数的分类( dimAA=2)

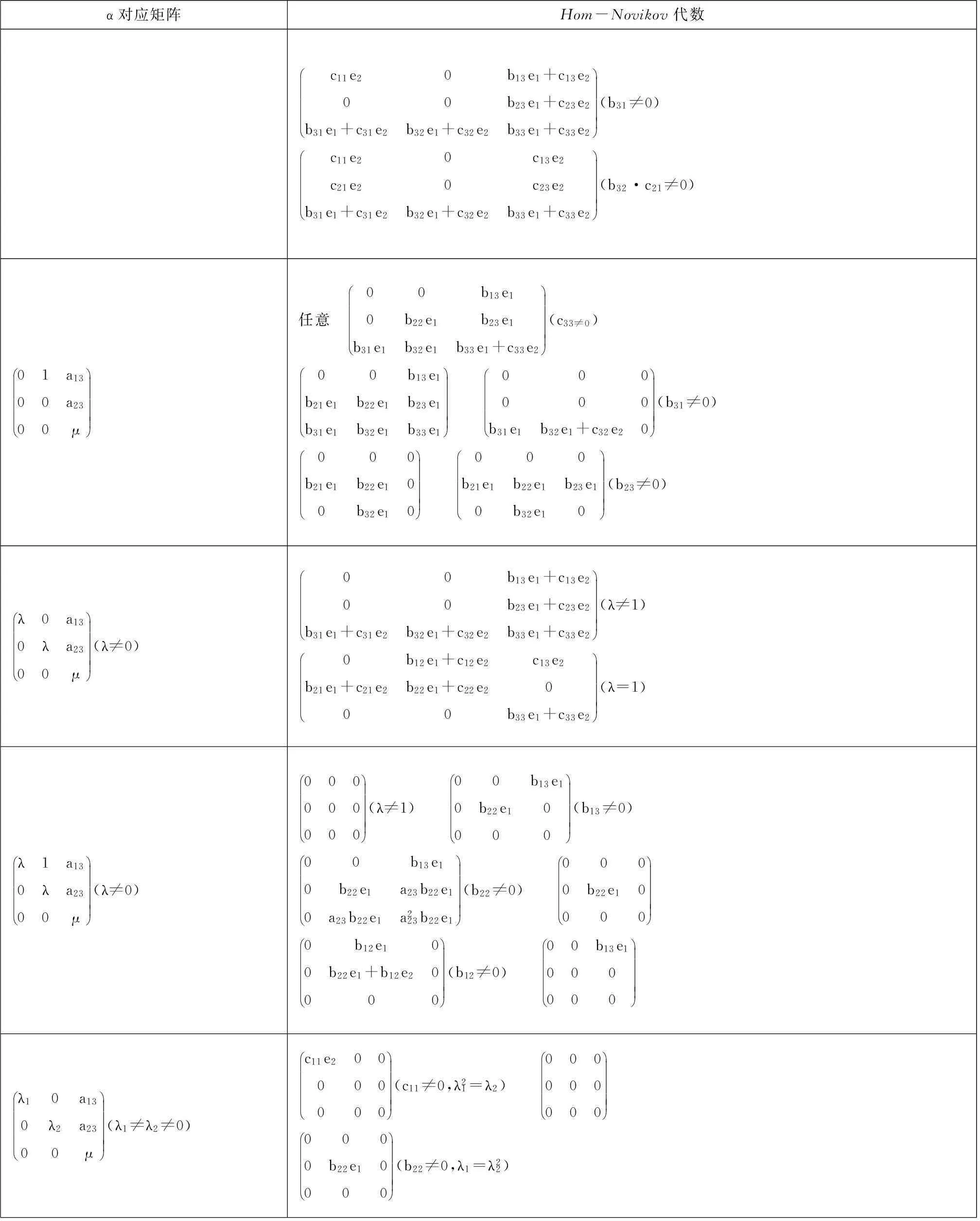
续表

参考文献：

[1]Frégier Y,Aron G.On Hom-type algebras[J].Journal of Generalized Lie Theory and Applications,2010(4):16.

[2]Yau D.Enveloping algebras of Hom-Lie algebras[J].Journal of Generalized Lie Theory and Applications,2008,2(2):95-108.

[3]Makhlouf A,Silvestrov S.Hom-algebra structures[J].Journal of Generalized Lie Theory and Applications, 2008,2(2):51-64.

[4]Yau D.Hom-Novikov algebras[J].Journal of Physics A Mathematical and theoretical,2011,44(8):202-222.

(责任编辑:陈衍峰)