水下爆炸冲击波数值模拟的网格尺寸确定方法

第一作者张社荣男，教授，1960年生

通信作者王高辉男，讲师，1986年生

邮箱：wanggaohui@whu.edu.cn

水下爆炸冲击波数值模拟的网格尺寸确定方法

张社荣1，李宏璧1，王高辉1,2，孔源1

(1.天津大学水利工程仿真与安全国家重点实验室，天津300072; 2.武汉大学水资源与水电工程科学国家重点实验室，武汉430072)

摘要：网格尺寸对水下爆炸冲击波传播过程的数值模拟精度有较大影响，且不同当量下可接受的网格尺寸也有较大区别。通过研究不同比例爆炸距离处水下爆炸冲击波峰值、比冲量对有限元网格尺寸的依赖性，以“炸药半径与网格尺寸之比”作为网格尺寸划分依据，提出了一种对不同当量均具有较强适用性的网格尺寸确定方法；对数值结果的误差分析表明，采用炸药半径的1/3作为数值模型的网格尺寸，其计算精度可满足工程要求；同时通过对数值计算误差进行非线性拟合，得到了不同网格尺寸下冲击波峰值压力、比冲量的误差估计式，可为研究人员根据可接受的误差范围确定任意当量下合适的网格尺寸或估计数值计算的整体误差提供参考。

关键词：网格尺寸效应；峰值压力；比冲量；炸药量；比例爆炸距离

基金项目：国家创新研究群体科学基金(51021004)；国家自然科学基金(51379141)；天津市应用基础与前沿技术研究计划(13JCYBJC19400)；水利工程仿真与安全国家重点实验室开放基金资助

收稿日期：2014-01-08修改稿收到日期：2014-04-24

中图分类号:TV312文献标志码：A

A method to determine mesh size in numerical simulation of shock wave of underwater explosion

ZHANGShe-rong1,LIHong-bi1,WANGGao-hui1,2,KONGYuan1(1. State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China;2. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China)

Abstract:The numerical simulation accuracy of underwater explosion shock wave propagation depends on mesh size, and the acceptable mesh size varies with charge weight. Through analyzing the mesh size effect on different scaled distances of shock wave peak pressure and impulse, taking the ratio of explosive radius to grid size as a criterion to determine mesh size, a mesh size-determining method being suitable for various charge weights was proposed. The error analysis of numerical results showed that if taking one third of the explosive radius as the mesh size, the numerical accuracy can meet the requirements of engineering; in addition, through nonlinear fitting of numerical simulation errors, the error estimation formulas for peak pressure and impulse of shock wave under different mesh sizes are derived. These error estimation formulas provided a reference for researchers to select an appropriate mesh size according to the charge weight and the acceptable error range or to estimate the accuracy of numerical results.

Key words:mesh size effect; peak pressure; impulse; charge weight; scaled distance

对水下爆炸冲击波传播过程进行数值模拟时，数值仿真的精度对有限元网格尺寸具有很大的依赖性[1]。通常为了提高计算精度，网格必须划分的足够小，且人工粘性的引入也要求计算网格划分的尺度不能太大，否则计算会忽略冲击波阵面信息，降低冲击波阵面峰值压力，从而降低计算的精度。当采用较小的精确网格尺寸时，单元数量增加，计算的最小时间步长也随之减小，降低计算效率并增加对计算机硬件水平的要求。因此当模型尺寸较大、爆炸工况较为复杂时，受计算机硬件、软件以及计算时间的限制，不得不采用较大的网格。

水下爆炸数值模拟中网格尺寸效应研究的核心就在于如何针对具体的爆炸问题确定合适的网格尺寸，以在确保计算精度的同时尽可能减少网格数量提高计算效率。目前，已有部分学者提出或研究过爆炸波模拟中的网格尺寸效应。如Krauthammer等[2]研究了爆炸冲击荷载作用下钢筋混凝土结构动力响应数值模拟中的网格尺寸、重力以及静力荷载等的影响，研究结果表明有限元模型的网格尺寸对于爆炸荷载作用下钢筋混凝土结构的变形和应力结果有较大影响；Shi等[1]研究了不同比例爆炸距离下空中爆炸冲击波特征参量——冲击波峰值压力、波前到达时间、冲击波冲量等对网格的依赖性，并提出了一个减小网格效应所造成数值误差的方法；Zukas等[3]探讨了网格尺寸大小、网格长宽比、网格形状等对数值模拟精度的影响；Jayasinghe等[4]采用显示非线性有限元程序，利用250mm的均匀网格研究了饱和砂土中桩基础的动态响应；Luccioni等[5]讨论了利用流体力学软件模拟预测爆炸荷载时的网格尺寸效应，认为100mm的网格尺寸就可以较为精确的模拟爆炸荷载的传播规律，而较粗的网格尺寸则仅仅可以用来定性的模拟爆炸荷载在城市复杂环境中的传播规律；Wang等[6]采用100 mm的网格对比研究了水下和空中爆炸作用下混凝土重力坝的动力响应规律；余晓菲等[7]采用MSC.DYTRAN研究了50mm、70mm等网格尺寸下水下爆炸冲击波峰值的计算误差，并分析了爆炸荷载作用下加筋圆柱壳的动态响应；龚顺风等[8]采用10 mm级的网格建立了钢筋混凝土柱的数值模型，并阐述了空中近爆作用下钢筋混凝土柱的损伤机理。可见，不同研究者在研究中使用的网格尺寸有较大差别。这一方面是由于不同问题的数值模拟可接受的误差范围有较大区别，另外则是因为爆炸问题的网格尺寸效应与爆炸所发生的环境介质(水体、空气、岩土体等)有一定关系，且与炸药量有较大关系。已有文献对网格尺寸效应的研究往往针对某一特定当量，故提出的网格尺寸在炸药当量改变时其使用有较大的局限性。

为提出一种对不同当量炸药水下爆炸问题均具有较强适用性的网格尺寸确定方法，本文基于非线性显示动力分析程序AUTODYN平台，建立了不同炸药量下的水下爆炸数值模型，对比分析了不同网格尺寸和不同比例爆炸距离处冲击波峰值压力和比冲量对有限元网格尺寸的依赖性，提出了一种对不同炸药当量均具有较强适用性的网格尺寸确定方法，数值计算结果的误差分析表明该方法合理可行，并通过对不同当量下的数值计算误差进行非线性拟合给出了水下爆炸冲击波峰值压力、比冲量计算误差与网格尺寸的关系曲线及误差估计式。

1材料模型及状态方程

1.1　炸药

在爆轰性能的考察和计算中，炸药爆轰产物的状态方程必不可少，在爆轰高温高压条件下，知道某时刻产物的组成和各组分的热力学参数，即可按照某种混合法则建立爆轰产物的状态方程。高能炸药材料采用JWL状态方程[9-11]描述了爆轰压力P和每单位体积内能E及相对体积V的关系：

(1)

式中：P为爆轰压力；V为爆轰产物体积和炸药初始体积之比；e为炸药的初始内能；A、B、R1、R2、ω为特征参数，各参数取值如下：A=3.738×1011Pa，B=3.747×1011Pa，R1=4.15，R2=0.9，ω=0.35，D=6.93×103m/s，e=5.999×109J/m3，PCJ=2.10×1010Pa，ρ0=1.63×103kg/m3。

1.2　水

炸药在水介质中爆炸时，在装药内形成高温高压的爆轰产物，其压力远远大于周围水介质的静压力，在水介质中会产生水中冲击波和气泡脉动现象。水介质采用多项式状态方程[12-13]进行描述，其形式根据水所处状态的不同而定。

当水为压缩状态(μ>0)时，其状态方程为：

(2)

当水为膨胀状态(μ<0)时，其状态方程为：

P=T1μ+T2μ2+B0ρ0e

(3)

式中：μ=ρρ0-1，ρ0是初始密度；A1、A2、A3、B0、B1、T1和T2是由AUTODYN材料库直接赋值的常数；e是比内能，其定义式如下：

(4)

式中，ρ和h分别是水的密度和深度，g和p0分别是重力加速度和大气压强。各参数取值如下：ρ0=1×103kg/m3，A1=2.2×109Pa，A2=9.54×109Pa，A3=1.457×1010Pa，B0=0.28，B1=0.28，T1=2.2×109Pa，T2=0 Pa。

2冲击波经验公式

Zamyshlyaev[14-15]在其关于水下爆炸问题的权威著作《Dynamics Loading in Underwater Explosion》中系统总结了当时水下爆炸问题试验研究及数值研究的成果，对Cole[16]的研究成果作了进一步的发展，将水下爆炸的爆炸载荷分为5个阶段：指数衰减阶段、倒数衰减阶段、倒数衰减后段、气泡膨胀收缩阶段和脉动压力段，并给出了每个阶段相应的载荷计算公式，公式直观明了，且具有很高的计算精度，本文使用该公式验证和分析数值计算结果的精度。水下爆炸中，峰值超压往往比静水压力大几个数量级，因此对于浅水爆炸，静水压力可忽略不计，峰值超压也被简称为峰值压力。冲击波的压力时程曲线在某一点由0迅速攀升到峰值压力，接着又呈指数形式衰减，水下爆炸冲击波指数衰减阶段的冲击波压力时程曲线、峰值压力及比冲量依Zamyshlyaev给出的经验公式有：

P(t)=Pme-t/θ,t<θ

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

P0=Patm+ρgH0

(15)

(16)

式中：Pm为冲击波峰值压力，Pa；P(t)为冲击波压力，Pa；θ为冲击波的指数衰减时间常数(s)，它是冲击波压力峰值Pm衰减到Pm/e所需的时间，e=2.718 28为自然对数的底；Ish为冲击波比冲量，N·s/m2；W为TNT炸药质量，kg；R为测点到爆心的距离，m；R0为炸药初始半径，m；td为波前到达时间，s；tp为冲击波正压作用时间，s；P0为爆心处流体静水压强，Pa；Patm为大气压，Pa；c为水中声速，m/s；H0为爆心的初始深度，m。

3网格尺寸确定方法及其验证

3.1　数值计算模型

对于无限水域或自由空气中球形装药的爆炸问题，究其本质可作为一维问题模拟。这是因为在自由场中，球形炸药起爆后，冲击波会从起爆点沿着球体半径方向呈球状波向外传播，因此可以根据球对称性利用一维中心对称模型来模拟爆炸波的传播。利用对称性减少问题的维数，可显著减少网格数量，提高计算效率，这种处理使得在计算中采用mm级的精细网格成为可能，在较大的尺度跨度内取值对于增强网格尺寸效应研究的说服力是必要的。本文利用AUTODYN中的一维楔体中心对称单元(Wedge)模拟球形炸药在自由场中的爆炸问题。由于Zamyshlyaev计算公式不适用于比例爆炸距离小于0.4 m/kg1/3的情况，且当比例爆炸距离大于1.5 m/kg1/3时，爆炸冲击波对一般钢筋混凝土结构的损伤作用已较小。故本文仅在比例爆炸距离0.4~1.6 m/kg1/3范围内布置监测点。比例爆炸距离Z的定义式为：

Z=R/W1/3

(17)

式中，R为测点到爆心的距离，m；W为TNT炸药质量，kg。

文中所用数值计算模型如图1所示。

图1　自由场水下爆炸计算模型 Fig.1 Numerical model of free-field explosions in water

计算模型中起爆点位于炸药的中心，水和炸药均采用多物质Euler算法(Euler算法适合于描述液体和气体的行为，爆轰产物和水可在网格间流动，故大变形或者有流动的情形不会导致网格畸变)。为了消除人工截断边界的影响，在模型截断边界处施加透射边界条件(Transmit边界)，使得冲击波在人工截断边界处无反射。

3.2　网格尺寸确定方法的提出

为初步探究炸药当量与网格尺寸效应之间的关系，分别采用50 mm、100 mm、200 mm的网格对炸药量1 kg、100 kg、500 kg及1 000 kg的水下爆炸冲击波传播特性进行分析，并将数值计算结果与经验公式计算值进行对比分析，对采用50 mm、100 mm、200 mm…这种确定性数值进行网格划分所存在的问题做了简要分析。

图2给出了炸药量分别为1 kg、100 kg、500 kg及1 000 kg时不同网格尺寸下水下爆炸的冲击波峰值压力与经验公式的对比曲线。值得说明的是由于1 kg炸药的半径为52.7 mm，因此图2(a)中没有给出1 kg炸药100 mm及200 mm网格下的数值计算结果。由图2(a)~(d)对比可知，不同炸药量的水下爆炸问题对网格尺寸大小的依耐性不同。在同一网格尺寸下，炸药当量较大的情况下能获得较为精确的数值结果，而炸药当量较小时，则与经验公式计算值偏离较大。如对于50 mm的网格，1 kg、100 kg、500 kg、1 000 kg当量时比例爆炸距离0.4 m/kg1/3处冲击波峰值的数值解分别为53.92 MPa、145.83 MPa、157.01 MPa、160.75 MPa，与经验公式计算值相比，计算误差分别为69.07%、16.35%、9.93%、7.79%。

图2　不同当量及不同网格尺寸下冲击波峰值压力对比 Fig.2 Comparison of shock wave peak pressures of different mesh sizes and charges

可见，水下爆炸数值模拟的网格尺寸效应与炸药当量有较大关系，因此若采用50 mm、100 mm、200 mm…这样的确定数值进行网格划分，在炸药当量不同时其使用具有较大的局限性。为便于研究炸药当量对数值模拟网格尺寸效应的影响，本文特引入一无量纲参量λ来描述炸药半径与有限元网格尺寸之间的关系，并以“炸药半径与网格尺寸之比”作为网格尺寸划分依据：

(18)

式中R0为药包半径，Le为有限元模型的网格尺寸。

在3.3、3.4小节中通过数值解与经验值对比、数值解误差分析两个角度对采用“炸药半径与网格尺寸之比”作为网格尺寸确定方法的适用性及合理性进行了验证分析。

3.3　水下爆炸冲击波数值模拟网格尺寸确定及其验证

为验证上文提出的网格尺寸确定方法的可行性，探究其是否能适用于不同当量的情形，并在保证数值解能较为接近经验公式计算值的前提下确定“炸药半径与网格尺寸之比”的合适取值。以1 kg、100 kg、500 kg及1 000 kg炸药水下爆炸的问题为例，对该网格尺寸确定方法的适用性进行了验证分析。

图3分别给出了1 kg、100 kg、500 kg、1 000 kg的TNT炸药在自由场水下爆炸的冲击波峰值压力与经验公式计算值的对比曲线。从图3可以看出，随着比例爆炸距离的增加，冲击波峰值压力逐渐减小，这与图3中利用经验公式计算所得规律一致。此外，无论是炸药当量较小(1kg)还是炸药当量很大(1 000 kg)的情形，当有限元网格尺寸取为炸药半径的1/2倍或1倍(λ=2和λ=1)时，在比例爆炸距离较小的情况下，数值结果与经验公式计算值偏离较大；而当有限元计算网格的尺寸取为炸药半径的1/3(λ=3)时，比例爆炸距离0.4~1.6 m/kg1/3范围内数值计算所得的冲击波峰值压力与经验公式计算值均较接近，继续减小网格尺寸可使数值计算结果愈加接近经验公式计算值，但计算量也会显著增加。

图3　冲击波峰值压力数值解与经验值对比 Fig.3 Peak pressure comparison of numerical and empirical results

图4给出了1 kg、100 kg、500 kg、1 000 kg炸药水下爆炸时比例爆炸距离0.4~1.6 m/kg1/3处冲击波比冲量数值计算值与经验公式计算值的对比曲线。从图4可以看出，在比例爆炸距离0.4~1.6 m/kg1/3范围内，随着比例爆炸距离的增加，数值计算所得冲击波比冲量减小，这与经验公式预测值所示规律一致。当有限元网格取为1/3倍炸药半径时，数值计算结果已非常接近经验公式预测结果。由图3、图4可看出，当炸药半径与网格尺寸之比λ=3时，无论小当量1 kg、中等当量100 kg，还是大当量500 kg、1 000 kg的水下爆炸问题，冲击波峰值压力及比冲量数值计算结果均与经验公式计算值比较接近，这说明①本文采用的根据“炸药半径与网格尺寸之比”确定有限元网格尺寸的方法具有较强的适用性，对于不同当量，采用相同的λ值划分有限元模型的网格，均能获得精度较为相近的数值计算结果；②采用炸药半径的1/3作为网格尺寸时，不同当量下数值计算所得冲击波峰值压力和比冲量均与经验公式计算值差别不大。

图4　冲击波比冲量数值解与经验值对比 Fig.4 Shock wave impulse comparison of numerical and Empirical results

3.4　误差分析

为进一步给出依据λ值确定有限元模型网格尺寸时的数值计算误差，探究当λ=3(网格尺寸为炸药半径的1/3)时，数值计算误差能否满足工程要求，并给出任意λ值下数值计算的误差估计式，特针对冲击波峰值及比冲量的数值计算结果进行了误差分析。需要指出的是，因为缺乏爆炸试验数据，本文的误差分析是以已有冲击波经验公式(式(5)~(16))的计算值为准，分析数值计算结果偏离经验公式计算值的程度。

图5以1 kg、100 kg、500 kg、1 000 kg炸药水下爆炸为例，给出了比例爆炸距离0.4、0.8、1.2、1.6 m/kg1/3处冲击波峰值压力计算误差与λ的关系曲线。对比图5(a)~(d)可以发现：①冲击波峰值计算误差随着λ的增大而减小，也即网格尺寸越精细，数值计算误差越小；②采用相同的λ值进行网格划分，不同当量下数值计算误差基本一致，说明依据λ值确定有限元网格尺寸的方法对不同当量炸药的爆炸问题均具有较强的适用性，且能获得精度大致相当的数值结果；③比例爆炸距离较大处峰值压力的计算误差大于比例爆炸距离较小处，这是由于冲击波从近场传播至远场过程中由于不精细的网格而过快衰减误差不断积累所致；而且在λ较小的情况下(见曲线的弯曲段)，比例爆炸距离较大的监测点对应的误差曲线斜率明显小于比例爆炸距离较小的监测点，说明比例爆炸距离越远，冲击波峰值对网格的依赖性越小。因此，数值计算中可在近场区域采用较密网格而远场区域采用较大网格——近场区使用较密网格可避免冲击波在近场区过快衰减进而影响远场区的计算精度，利用远场区计算结果对网格依赖性较小的特点适当扩大网格以减小整体计算量——这正是爆炸问题数值模拟中常用的网格划分策略。

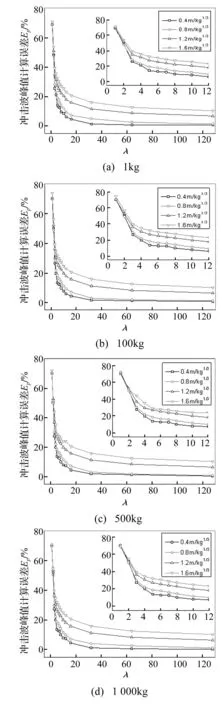
图5　冲击波峰值压力计算误差分析 Fig.5 Calculation error analysis of shock wave peak pressure

图6以1 kg、100 kg、500 kg、1 000 kg炸药水下爆炸为例，给出了比例爆炸距离0.4、0.8、1.2、1.6 m/kg1/3处冲击波比冲量计算误差与λ的关系曲线。对比图5和图6可以发现：不同比例爆炸距离处，冲击波峰值压力的计算误差有一定区别，而比冲量的计算误差没有明显区别。在比冲量计算误差与λ关系曲线的弯曲段，不同比例爆炸距离所对应曲线的斜率几乎一样，说明不同比例爆炸距离处比冲量的网格依赖性无显著区别。结合图5和图6可看出，当网格尺寸定为炸药半径的1/3时，冲击波峰值压力的计算误差约为35%，而比冲量的计算误差可控制在15%左右，这种计算精度可满足工程要求(实际中还可根据上文提到的在近场区域适当加密网格的办法提高峰值压力的计算精度)，说明采用炸药半径的1/3作为有限元网格尺寸在工程中是合理可行的。

前文已对不同网格尺寸下比例爆炸距离处0.4、0.8、1.2、1.6 m/kg1/3处冲击波比冲量计算误差与λ的关系进行了分析，得到了计算误差随比例爆炸距离变化而变化的一般规律。但是在具体数值计算中，研究者往往更关注于计算的整体误差而不是若干特定点的计算误差。由于不同比例爆炸距离处冲击波峰值压力的计算误差有一定区别，为了评价某一λ值下数值计算的整体误差，本文以各比例爆炸距离处冲击波峰值计算误差的平均值作为相应λ值下数值计算的整体误差，比冲量的计算误差也做了同样处理。基于这种处理，采用非线性拟合方式获得了爆炸冲击波峰值压力及比冲量整体计算误差与λ的关系曲线及相应的误差估计式。图中拟合曲线所用数据点为1 kg、50 kg、100 kg、250 kg、500 kg、1 000 kg炸药水下爆炸不同网格划分方式下的整体计算误差。

图6　比冲量计算误差分析 Fig.6 Calculation error analysis of shock waveimpulse

图7　冲击波峰值压力及比冲量计算误差拟合曲线 Fig.7 Fitting curves of numerical calculation errors about shock wave pressure and impulse

图7(a)给出的是冲击波峰值计算整体误差Ep的拟合曲线，相应的误差估计公式为：

Ep=69.699 46·λ-0.651 51

(19)

图7(b)给出了冲击波比冲量计算整体误差Ei的拟合曲线，相应的误差估计公式为：

Ei=31.610 78·λ-0.641 76

(20)

采用非线性拟合方式获得的冲击波峰值及比冲量整体计算误差拟合曲线所得的相关系数的平方分别为0.988 53和0.995 43，均在0.95以上，说明曲线拟合精度和可信度较高。利用这些误差估计式可方便的估算特定网格尺寸和炸药当量下数值模拟的精度，这可为研究者根据可接受的误差限值快速地确定所需要的网格尺寸或根据具体的有限元模型估计整体计算误差提供参考。

4结论

本文基于非线性显示动力分析程序AUTODYN平台，建立了不同炸药量、不同网格尺度下的水下爆炸数值模型，对不同比例爆炸距离处爆炸冲击波峰值、比冲量的网格尺寸效应进行了敏度分析和计算结果的误差分析，主要得到以下结论：

(1)网格尺寸对水下爆炸冲击波传播过程的数值模拟精度有较大影响。在一定的数值计算精度要求下，炸药当量越大，可使用的网格尺寸越大；

(2)本文以“炸药半径与网格尺寸之比”作为网格尺寸划分依据，提出了一种对不同当量均具有较强适用性的网格尺寸确定方法。对水下爆炸的数值模拟，当网格尺寸定为炸药半径的1/3时，计算精度可满足工程要求；对数值结果的误差分析也表明，当不同数值模型的“炸药半径与网格尺寸之比”相等时，不同当量情况下可得到数值精度相当的结果；

(3)本文以各比例爆炸距离处计算误差的平均值作为该网格尺寸下数值计算的整体误差，通过非线性拟合得到了冲击波峰值及比冲量计算误差的误差估计式，可为研究人员根据可接受的误差范围确定任意当量下合适的网格尺寸或根据计算模型网格尺寸估计数值计算的整体误差提供参考。

参考文献

[1]Yanchao S, Zhongxian L I, Hong H. Mesh size effect in numerical simulation of blast wave propagation and interaction with structures[J]. Transactions of Tianjin University,2008, 14(6)：396-402.

[2]Krauthammer T, Otani R K. Mesh, gravity and load effects on finite element simulations of blast loaded reinforced concrete structures [J]. Computers & structures,1997, 63(6): 1113-1120.

[3]Zukas J A, Scheffler D R. Practical aspects of numerical simulations of dynamic events: effects of meshing[J]. International Journal of Impact Engineering,2000, 24(9): 925-945.

[4]Jayasinghe L B, Thambiratnam D P, Perera N, et al. Computer simulation of underground blast response of pile in saturated soil [J]. Computers & Structures, 2013, 120: 86-95.

[5]Luccioni B, Ambrosini D, Danesi R. Blast load assessment using hydrocodes [J]. Engineering Structures,2006, 28(12): 1736-1744.

[6]Wang G, Zhang S, Kong Y, et al. A comparative study on the dynamic response of concrete gravity dams subjected to underwater and air explosions[J]. Journal of Performance of Constructed Facilities, 2014.

[7]余晓菲，刘土光，张涛，等. 水下爆炸载荷作用下加筋圆柱壳的响应分析[J]. 振动与冲击, 2006, 25(5):106-115.

YU Xiao-fei, LIU Shi-guang, ZHANG Tao,et al. Response analysis of cylindrical shell subjected to underwater explosion shock waves [J]. Journal of Vibration and Shock,2006, 25(5):106-115.

[8]龚顺风，夏谦，金伟良. 近爆作用下钢筋混凝土柱的损伤机理研究[J]. 浙江大学学报(工学版), 2011(8): 1405-1410.

GONG Shun-feng, XIA Qian, JIN Wei-liang. Investigation on damage mechanism of RC column under close-in explosion [J]. Journal of Zhejiang University (Engineering Science),2011(8): 1405-1410.

[9]John B. Numerical modelling of shock wave and pressure pulse generation by underwater explosions[J]. NASA,1998(19990007753).

[10]Larcher M. Simulation of the effects of an air blast wave[J]. JRC Technical Note, Pubsy JRC41337, Ispra, 2007.

[11]石磊，杜修力，樊鑫. 爆炸冲击波数值计算网格划分方法研究[J]. 北京工业大学学报, 2010(11): 1465-1470.

SHI Lei, DU Xiu-li, FAN Xin. A study on the mesh generation method for numerical simulation of blast wave [J]. Journal of Beijing University of Technology,2010(11):1465-1470.

[12]Barras G, Souli M, Aquelet N, et al. Numerical simulation of underwater explosions using an ALE method. The pulsating bubble phenomena[J]. Ocean Engineering, 2012, 41: 53-66.

[13]胡毅亭，贾宪振，饶国宁，等. 水下爆炸冲击波和气泡脉动的数值模拟研究[J]. 舰船科学技术，2009(2): 134-140.

HU Yi-ting, JIA Xian-zhen, RAO Guo-ning, et al. Numerical study of underwater explosion shock wave and bubble pulse [J]. Ship Science and Technology,2009(2): 134-140.

[14]刘科种，徐更光，辛春亮，等. AUTODYN水下爆炸数值模拟研究[J]. 爆破, 2009(3): 18-21.

LIU Ke-zhong, XU Geng-guang, XIN Chun-liang,et al. Research on numerical simlnation in underwater explosion by Autodyn [J].Blasting,2009(3): 18-21.

[15]Zamyshlyaev B V, Yakovlev Y S. Dynamic loads in underwater explosions[M]. Sudostroenie, Leningrad, 1973.

[16]Cole R H. Underwater explosions [M]. New York: Dover Publications, 1965.