赏析2015年高考安徽物理卷第24题

赏析2015年高考安徽物理卷第24题

杨钧捷

(江苏省海门中学江苏 南通226100)

收稿日期：(2015-06-14)

1试题及解析

【例1】(2015年高考安徽卷第24题)由3颗星体构成的系统，忽略其他星体对他们的作用，存在着一种运动形式：3颗星体在相互之间的万有引力作用下，分别位于等边三角形的3个顶点上，绕某一共同的圆心O在三角形所在的平面内做相同角速度的圆周运动(图示1为A，B，C 3颗星体质量不相同时的一般情况)．若A星体质量为2m，B和C两星体的质量均为m，三角形的边长为a．求：

(1)A星体所受合力大小FA；

(2)B星体所受合力大小FB；

(3)C星体的轨道半径RC；

(4)3星体做圆周运动的周期T．

图1

参考答案：如图2所示，以BC连线为x轴，过BC中点D且垂直于BC方向为y轴建立直角坐标系xDy．

(1)根据万有引力定律，A星体所受B与C星体引力大小相等

则A星体受到的合力大小为

(2)B星体所受A与C星体引力大小分别为

方向如图2；

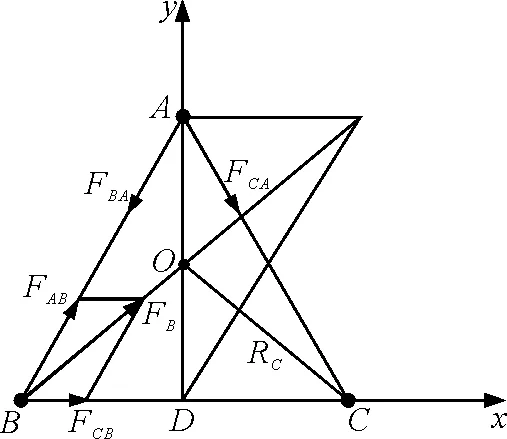
图2

则B星体受到的合力大小为

(3)通过分析可知，圆心O在中垂线AD的中点

或由

得出

(4)3星体运动周期相同，对C星体，由

得

2拓展研究

试题的图1中给出的是3星质量全部不等，即(mA≠mB≠mC)的一般情况下的运动形式，而试题的问题中则是研究3星质量不全部相等(mA=2m，mB=mC=m)条件下的运动形式，为了对3星圆周运动这种特殊的运动有更深入地了解，下面对质量mA≠mB≠mC的一般条件下3星圆周运动进行分析与计算．

拓展试题：由3颗星体构成的系统，忽略其他星体对他们的作用，存在着一种运动形式：3颗星体在相互之间的万有引力作用下，分别位于等边三角形的3个顶点上，绕某一共同的圆心O在三角形所在的平面内做相同角速度的圆周运动．如图1所示，为A，B，C 3颗星体质量不相同时的一般情况．A，B，C 3星的质量分别为mA，mB，mC，且mA≠mB≠mC，求3星绕圆心O做圆周运动的周期T．

解析：位于等边三角形顶点处3星以相同的角速度ω绕共同的O做圆周运动，根据质心运动定理可知，圆心O为三星系统的质心．

如图3所示，以D表示mB和mC的质心，则有

图3

过D作DE//AC，过D作DF//AB，则△BDE与△CDF均为等边三角形，AEDF为平行四边形，得出

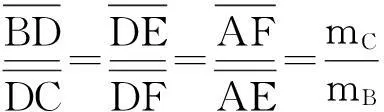
(1)

在△ABD中，根据余弦定理可得

以O表示A，B，C 3星系统的质心，则O点在AD上，且有

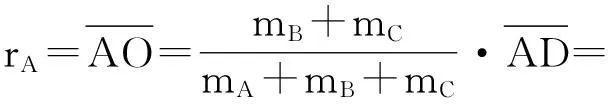
(2)

同理可得

(3)

则mB对mA的作用力是

mC对mA的作用力是

得出

结合式(5)，得出

即fBA和fCA的合力fA的作用线通过质心O，fA的大小为

(4)

同理可证，fB的作用线也通过质心O′，且

(5)

由式(2)～(5)得

(6)

同理可证

(7)

由f=mω2r可知，(6)、(7)二式说明，mA，mB，mC3星可在由初位置所决定的平面内保持相对位置不变绕质心O做匀速圆周运动．做圆周运动的角速度ω亦可由(5)、(6)二式得出为

则3星绕系统质心O做圆周运动的周期为

(8)

当mA=2m，mB=mC=m时，代入式(8)，得

即为高考试题第(4)问的结果．

3试题评析及启示

(1)本题以宇宙中的三星系统为背景命题, 考查了匀速圆周运动、力的合成与分解、牛顿第二定律、万有引力定律和向心力公式等主干知识．试题的情境具有乍一看熟悉、细思量陌生的特点．熟悉之处在于历年的高考题中多次考查了多星问题，是高考复习的重点内容，例如2006年广东高考题考查了质量相等的3星问题的运动形式．

【例2】(2006年高考广东卷第17题)宇宙中存在一些离其他恒星较远的、由质量相等的3颗星组成的三星系统，通常可忽略其他星体对它们的引力作用．已观测到稳定的3星系统存在两种基本的构成形式：一种是3颗星位于同一直线上，两颗星围绕中央星在同一半径为R的圆轨道上运行；另一种形式是3颗星位于等边三角形的3个项点上，并沿外接于等边三角形的圆形轨道运行．设每个星体的质量均为m.

(1)试求第一种形式下，星体运动的线速度和周期．

(2)假设两种形式星体的运动周期相同，第二种形式下星体之间的距离应为多少？

陌生之处在于本题中3星的质量不再全部相等，运动形式较之质量相等的3星运动要复杂，要求学生能够将多星运动问题的分析方法迁移到新的运动情境中，本题是一道能够鉴别学生物理规律的理解能力，面对新颖物理情境的分析能力、解决陌生问题的迁移能力的优秀试题，充分体现了压轴题的选拔功能．

(2)通过试题与拓展研究的对比分析可以看出，拓展研究中3星质量全部不等(mA≠mB≠mC)的一般条件下，要用到竞赛中的质心定义，数学运算也较为复杂，而在高考试题中3星质量则是不全部相等(mA=2m，mB=mC=m)，从而使3星运动分析具有了几何对称性，规避了质心这个高考超纲概念，避免了繁琐的数学运算，由此可以看出高考试题的匠心独具．高考试题通过设置具有梯度的4个问题，引导学生有效地进行方法的迁移、逐步深入地分析问题，使试题有了一定的区分度，具备了较好的选拔功能．

(3)高考压轴题肩负着选拔优秀学生的功能，具有应用型和能力型相结合的特点，对学生理解能力、分析综合能力以及应用数学处理物理问题的能力要求较高，考虑到竞赛题也具有这些特点．因此，在历年高考中，一些知识点属于高考范畴的情境新颖的竞赛题通过改编出现在高考压轴题中也就不足为奇．可以认为这是高考压轴题的一种命题导向，启示我们在日常教学中要去研究一些适合高考复习用的竞赛题，特别要关注一些考点落在高考考纲范畴内的竞赛题的情境和模型，对这类试题进行深入研究和改编，使之成为有利于培养学生探究能力、方法迁移能力、建立模型能力的试题，进而有效地培养学生把所学的知识运用到不熟悉的地方去的能力．

物理技术研究